基于Cube压头压入识别Ti基涂层材料断裂韧性

石新正

摘 要：基于Cube压头的Ti-SiO2-TiO2和Ti-TiO2-SiO2涂层材料压痕实验并利用Dukino、Pharr、Harding和Zhang提出的断裂韧性计算公式计算两种涂层材料的断裂韧性值，通过四个公式断裂韧性计算结果与参考文献结果对比验证其有效性。结果显示Dukino、Pharr、Harding和zhang公式最大误差分别为6.6%、14.1%、2.9%和26%，因此Dukino和Harding公式识别精度比较高，可以适用于涂层材料断裂韧性的测试。

关键词：Cube压头；涂层材料；断裂韧性

DOI：10.16640/j.cnki.37-1222/t.2017.15.007

0 引言

近年来，涂层材料在军事工业、机械加工业和航空工业等行业中发挥着极其重要的作用。在实际工作环境中，涂层固有的脆性与外部诸多因素的作用会导致基体界面上的涂层系统脱落失效，从而涂层的增韧技术已成为研究的难点和热点问题。由于涂层材料的耐磨性与裂纹的产生和扩展有着密切的联系，涂层材料的断裂韧性是衡量涂层材料好坏的一个重要力学性能参数，但是传统的断裂韧性测试方法由于受到识别试样尺寸、形状以及测试精度的制约已经不能满足涂层材料的测试要求，因此识别微小尺度涂层材料的断裂韧性发展成为国内外学者研究涂层材料力学性能的焦点问题。

1 几种识别脆性材料断裂韧性的模型

Evans和Lawn等人利用Vickers和Berkovich压头压入实验，提出了测量脆性材料断裂韧性的公式

（1）

式中：E/H为材料弹性模量与硬度的比，Pm为最大加载力，c为裂纹长度，为与压头有关的系数。

Pharr等研究发现Vickers压头在加载大于或者等于10N时脆性材料压痕裂纹长度大于或等于100μm，加载力与裂纹之间有一个极限，对于同一脆性材料在一定加载下才会出现裂纹， Vickers和Berkovich压头压入陶瓷材料最小加载力极限250mN才能产生裂纹，而对于一些涂层或者薄膜材料，就需要在不被基体影响的前提下使用较小的加载力来压入材料产生裂纹，因此Vickers和Berkovich压头就不能满足测试以上材料断裂韧性的要求，他们通过Cube压头实验分析压头角度与公式（1）中的关系，测算出KIC的公式

（2）

（3）

式中：为材料泊松比，为压头面角。

Harding等研究发现压头锥角越小，脆性材料裂纹越容易开裂，并采用Cube压头进行了压入试验，测得Cube压头压入产生裂纹的最小极限载荷小于Vickers和Berkovich压头的压入载荷，Cube压头在小于10mN的载荷下压入脆性材料仍然可以产生裂纹， 同时他们发现利用公式（1）的系数计算出的结果与实验值相差比较大，因此他们基于Cube压头给出了修正系数=0.04。

D.J. Morris等使用Vickers、Berkovich和Cube压头对涂层材料进行压入试验发现在测试低应力强度因子的涂层材料时，Cube压头比Vickers、Berkovich压头压入实验时更容易产生裂纹，另外Cube压头压入时裂纹影响区比较小，所测材料的断裂韧性比Vickers、Berkovich压头测试的结果精确。因此可以基于Cube压头使用较小的加载力来识别涂层材料断裂韧性。

Laugier等利用四棱锥Vickers压头实验并综合考虑a，l和c以及E/H的影响给出了计算脆性材料的计算公式：

（4）

式中：a、c、E、H和Pm含义与式（1）相同，其中l =c-a，λ=0.015。

然而Laugier等在压入试验时的加载载荷在100mN以上才产生裂纹，Dukino等在满足公式（4）的基础上，提出基于三棱锥压头使用较小的加载力压入试验修正公式，其修正系数λ=0.016。

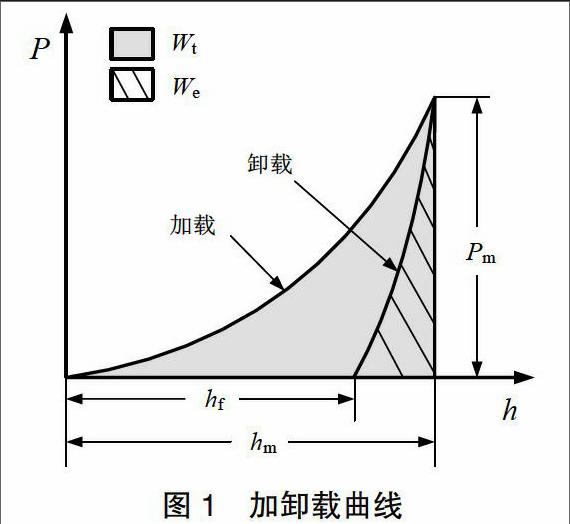
Zhang等利用基于Cube压头压入脆性材料时的加卸载曲线计算出了加卸载时的加载功Wt与卸载功We，使用We /Wt来替代公式（1）中E/H，加卸载曲线如图1所示，并建立了计算断裂韧性的公式（5）。

（5）

式中：α=0.0695，Pm和c与式（1）含义相同。

2 试验验证

2.1 涂层材料

涂层材料的结构以Ti为基体，涂层为TiO2和SiO2，附着层为Ti或TiO2。以Ti为基体交替喷涂TiO2和SiO2，最终形成Ti基体， SiO2-TiO2交替涂层，和Ti基TiO2-SiO2交替涂层的材料，Ti-SiO2-TiO2涂层材料厚度为1515nm，Ti-TiO2-SiO2涂层材料厚度为1575nm。

2.2 压入试验

为了避免基体对实验结果的影响，基于Cube压头采用Nano公司的超低载荷纳米压痕仪进行压入试验，Cube压头的弹性模量Ei=1140GPa和泊松比νi=0.07。

识别涂层材料的弹性模量E和硬度H时压入深度应小于涂层厚度的1/10，因此压入深度选择150nm，加载和卸载速率为450nm/min，每种材料压入实验重复20次。测试结果使用O-P方法进行计算涂层的弹性模量和硬度。

在断裂韧性测试时设定三种最大加载力分别为10mN、20mN和30mN，加载速率为10mN/min，卸载速率为120Mn/min，最大加载荷时保载10s，为了避免偶然误差的发生，每种涂层材料试验重复20次。

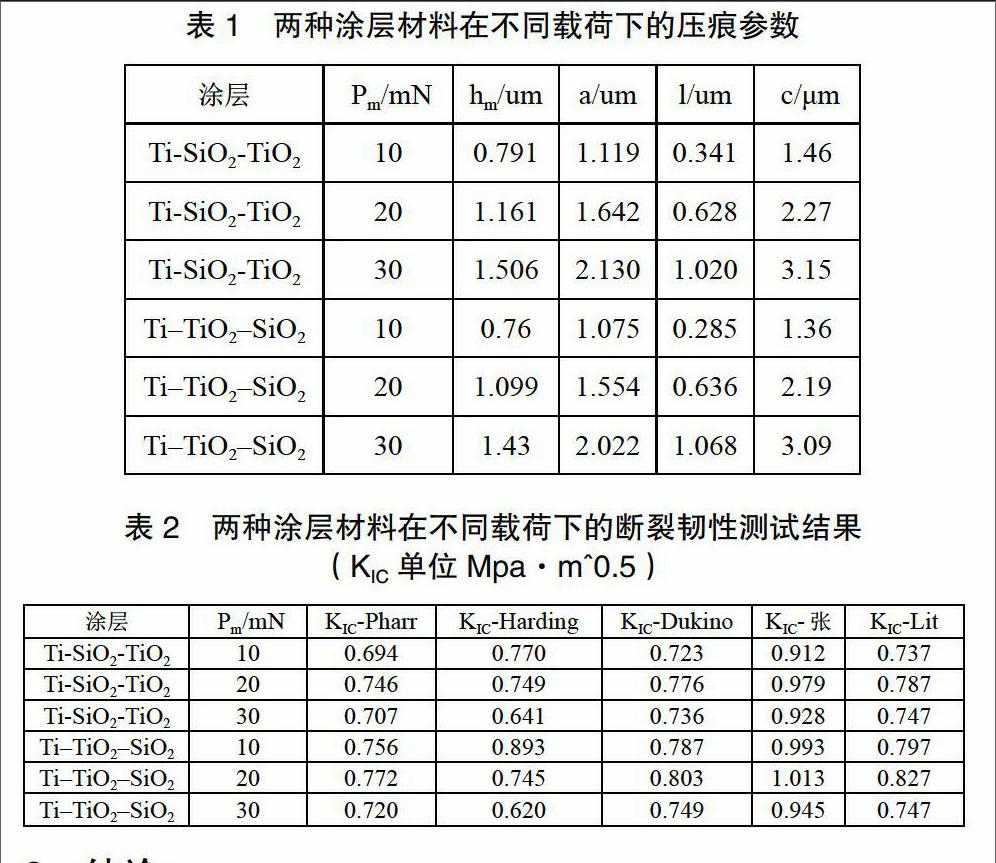
2.3 压入实验结果

使用电子扫描显微镜对基于Cube压头压入实验的两种涂层材料在不同载荷下的表面压痕和裂纹进行观察与测量，裂纹均未出现横向裂纹，并且裂纹开裂比较好，表1是两种涂层材料在三种不同载荷下压入深度和产生的裂纹长度。利用Pharr、Harding、Dukino、Zhang等提出的基于Cube识别涂层材料断裂韧性计算公式最后得出的Ti-SiO2-TiO2涂層材料和Ti-TiO2-SiO2涂层材料断裂韧性值，表2为断裂韧性值测试结果。通过本文介绍的四个断裂韧性计算公式的计算结果与文献给出的断裂韧性值比较，得出每个公式的误差。