SVM用于非线性系统故障诊断

2021-04-19吴庆涛韩春松丁传东

齐齐哈尔大学学报（自然科学版） 2021年3期

吴庆涛，韩春松，丁传东

（齐齐哈尔大学机电工程学院，黑龙江齐齐哈尔 161006）

支持向量机（SVM，Support Vector Machine）最早用于线性系统数据分类，引入核函数后，SVM 具备了处理非线性系统数据的能力，又因其理论完善，需求训练样本少，分类效果好的特点，近年来被广泛的用于非线性系统故障诊断。梅恒荣等[1]使用IPSO 算法优化SVM 的参数，有效地提高模拟电路故障诊断的分类准确率和收敛速度，缩短分类时间；张建等[2]用改进的免疫算法优化支持向量机惩罚因子、松弛变量及核函数参数用于某型航空发动机磨损故障诊断；许迪等[3]提出一种量子遗传算法优化的SVM 算法，用于滚动轴承的故障诊断；胡晓依等[4]在卷积神经网络基础上，融入支持向量机和深度学习的模型优化技术，提出适于轴承故障诊断的CNN-SVM 深度卷积神经网络模型；张龙等[5]利用VMD 算法对振动信号进行分解处理，作为特征向量输入到PSO 优化的SVM 中，实现滚动轴承故障诊断；林煜凯[6]提出了基于集成模态经验分解（EEMD）的改进布谷鸟搜索算法（ICS）和SVM 的故障诊断方法，用于齿轮箱故障诊断。本文旨在通过数据分类实验，对比分析SVM 线性核函数和径向基核函数的数据处理性能，确认适用于非线性系统故障诊断的核函数。

1 支持向量机理论

对于线性可分的训练集样本 train ={( x1, y1),( x2, y2), …, ( xn, yn)}，且类别 yi∈{+ 1 , - 1}，SVM 的目的就是寻求一个最优超平面 ωx + b=0，要求这个最优平面满足以下两个条件：

（1）将两种类别数据准确分开，即：

（2）保证两类别数据之间的距离最大，即φ (ω ,ξ )的值最小：

式中，C>0 且为一常数，ξ 称为惩罚因子。

而后引入拉格朗日系数αi( i = 1,2, …, l)，再根据KKT（Karush-Kuhn-Tucker）取得极值的条件和优化方程求解的对偶性原理，最终上述求解最优超平面的公式变为

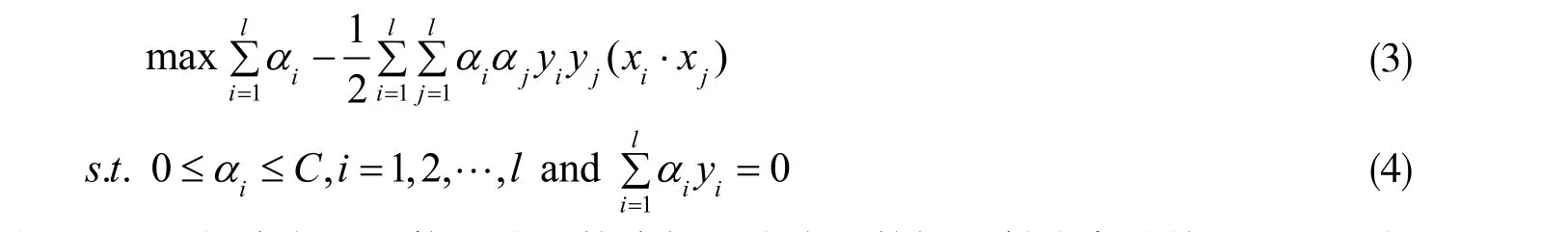
那么对于非线性分类问题，SVM 的解决方法是使用核函数将低维非线性数据映射成高维特征空间，变成线性可分数据。加入核函数后，求解最优超平面的公式变为

2 实验探究

本文选取4 组数据来完成SVM 线性核函数和径向基核函数分类性能对比实验，结果如图1, 2 所示。同时为了实验结果更易于对比，又将分类准确率和用时以数据形式呈现在表1 中。在实验中，SVM 的惩罚系数C 设置为100，径向基核函数参数设置为1。下面对4 组数据以及实验结果进行简要分析和说明。

图1 线性可分数据和线性不可分数据SVM 分类结果

（1）线性可分数据。在两段区间[1,3]和[4,5]中随机产生数据，且[1,3]区间产生数据样本类别为+1，[4,5]区间产生数据类别为-1，最终产生训练样本数据110 个，测试样本数据40 个。图1 中的a 显示的是线性核函数分类结果图，图1 中的c 显示的是径向基核函数分类结果图，且表1 中显示两个核函数分类结果都是100%，所以两种核函数都能将线性可分数据有效分类，但表1 中显示径向基核函数用时短。

（2）线性不可分数据。3 段区间[2,3]、[3,4]和[4,5]随机产生数据，[2,3]区间和[4,5]区间产生数据样本类别为+1，[3,4]区间产生数据类别为-1，最终产生训练样本数据60 个，测试样本数据60 个。图1(b)是线性核函数分类结果图，图1(d)是径向基核函数分类结果图，由图可以看出径向基核函数能够将数据圈出分类，而线性核函数无法有效分类，表1 中也显示出相比于径向基核函数，线性核函数的分类准确率低且用时长。

（3）Iris 数据集。Iris 也称鸢尾花卉数据集是公认的分类实验数据集，是由Fisher 收集整理，这个分类数据集可在UCI 数据库中下载。

Iris 数据类别分为3 类，setosa，versicolor，virginica。每类植物有50 个样本，共150 个，每个样本有4个属性，分别为花萼长、花萼宽、花瓣长、花瓣宽。实验中取setosa 数据的类别为+1，其余类别为0。

图2(a)是线性核函数分类结果图，图2(c)是径向基核函数分类结果图，能看到两种核函数都将数据有效分开，且表1 数据也显示分类准确率均为100%，所以两种核函数都能对Iris 数据进行有效分类，当然径向基核函数在用时上更胜一筹。

（4）轴承故障数据。轴承数据来自于美国西储大学轴承数据中心，是在故障诊断领域公认的数据，在诸多文献中都有使用。

数据测量平台有4 种负载下相应就有4 个转速，分别为1 797, 1 772, 1 750, 1 730 r/min；每种负载下的轴承有3 个损伤位置，分为内圈（IF）、外圈（OF）、滚动体（RF）；而每个损伤位置又有3 种损伤直径，即0.177 8, 0.355 6, 0.533 4 mm 三种。

实验选用的数据，是在大负载下，转速1 730 r/min，轴承损伤位置选为内圈（IF），损伤直径选为0.533 4 mm，而采样频率选为12 kHz，选取驱动端数据（DE）和风扇端数据（FE）。训练样本1 500 组数据，其中正常样本1 000 组，故障样本500 组；测试样本1 000 组数据，其中正常样本500 组，故障样本500 组。正常样本类别为+1，故障样本类别为-1。

图2(b)是线性核函数分类结果图，图2(d)是径向基核函数分类结果图，由图可以看出径向基核函数比线性核函数分类界限更清晰，且表1 体现出径向基核函数的分类准确率更高，且用时更短。