小学数学类比推理或然性及其对策探析

蔡静

摘要：类比推理是合情推理，具有或然性。小学生以具体形象思维为主，容易忽视或然性，出现错误。教师在引导学生感悟类比推理或然性的同时，更要抓核心问题、融演绎推理、引深度思考，促使学生的思维从表层到实质、从形似到神似、从低阶到高阶。

关键词：类比推理;或然性;核心问题;演绎推理;深度思考

一、缘起：真的可以这样“以此类推”吗？

笔者执教六年级时发现，学生在解答“甲比乙多14，则乙比甲少几分之几？”这样的问题时，错误率较高。大部分学生会认为答案是14。学生的主要观点是“甲比乙多多少就是乙比甲少多少”“两个数相差的一样多”。不少教师会从单位“1”的角度向学生解释，强调这样的分数关系不能简单地画等号。学生当堂能听懂，但过几天又会回到原来的想法，出现相同的错误。一次，笔者采访一位学生：“你是怎么知道甲比乙多14就是乙比甲少14的？”学生很自信地回答：“这很容易推理的。两个数比较，相差的部分是不变的，那理所当然，甲比乙多几分之几就是乙比甲少几分之几。”笔者再追问：“真的是这样吗？”学生没有陷入思考，脱口而出：“我们在一年级时就知道，甲比乙多4个就相当于乙比甲少4个，这里不就是以此类推吗？”

原来，学生在思考这类问题时，并没有进行严密的思考，而是不管三七二十一，将已有的认识经验类推到新的问题上来。真的可以这样“以此类推”吗？

二、思考：类比推理的或然性

这里的“以此类推”实际上就是类比推理，是根据两个或两类不同对象的某些方面（如特征、属性、关系等）相同或相似，推导或猜出它们在其他方面可能相同或相似的思维形式。类比推理的客观基础就是事物系统之间各属性的普遍联系以及这些联系之间存在的相似性和可比较性，只要两个对象有某个方面的相似性（包括形式上的相似、结构上的相似、内容上的相似等），就可以类比。类比推理是小学阶段常用的一种推理方法，它能帮助学生内化数学知识、优化问题解决、实现数学应用。但必须注意的是，类比推理是合情推理（也称或然推理），有时候虽然看起来合情合理，结论好像（应该）是对的，但本质上条件和结论没有必然的联系，即类比推理具有或然性。

类比推理是一种生动、活泼的思维方式，符合小学生的年龄与身心发展的特征。在小学数学课堂应用类比推理开展教学，能够帮助学生更好地掌握和理解知识，培养其推理能力，促进其思维发展。但小学生的逻辑思维不够严密、成熟，在由一般到一般、个别到个别的过程中很容易将属性迁移，忽视或然性，造成错误。

例如，有学生在学习了乘法分配律后会类推出除法也有这样的运算律，在看到100÷（20+30）时，会写成100÷20+100÷30;在学习2和5的倍数特征时，发现关注的都是个位，从而类推出3的倍数特征是个位是3、6、9;在学习了“长方形的面积=长×宽”“正方形的面积=边长×边长”后，会推想“平行四边形的面积=底×邻边”;等等。这些都是小学数学中类比推理或然性的体现，也是学生常常容易忽略和出错的点。它们就像缠绕住学生思维发展的藤蔓，阻碍了学生整体数学素养的提升。

三、实践：突破樊篱，探寻出路

（一）从表层到实质：抓核心问题

类比推理中的或然性常常出现在学生思维易混淆之处，特别是当某些概念有多重属性的时候，学生往往会被表层的现象迷惑，而忽略实质的差异。如本文一开始的问题，就是学生将“两个数量相差的量不变”错误类推到“两个数量相差的分率不变”所致。从表层看，是类推过程中偷换了概念，但究其本质，核心问题是学生对分数表示“率”与“量”这两重属性混淆不清。因此，要从表层错误入手，抓住学生思维漏洞的实质，依据核心问题展开教学。具体过程如下：

师（出示“甲比乙多14”“甲比乙多14元”）这两个条件一样吗？

生不一样。前一个14反映的是甲与乙相差的分率;后一个14反映的是甲比乙多的具体的数量。

生“甲比乙多14”这句话里，乙是单位“1”，可以将乙看成4份，甲比乙多1份，甲就是5份。

师很好！在低年级时我们学过，甲比乙多4个可以说成乙比甲少4个，你觉得这两个条件都可以这样反过来说吗？

生第二个可以， “14元”是具体的数量，可以和以前一样说成“乙比甲少14元”;但第一个是分率，应该不能这样类推。

生第二个不能这样类推。根据前面同学的回答可以知道，乙是4份，甲是5份，“乙比甲少几分之一”的单位“1”是甲，要去除以5，算式应该是（5-4）÷5，结果是15。

生是的，不管是甲比乙多1份，还是乙比甲少1份，相差的份数没变;但求分率时单位“1”发生了变化，所以相差的分率也不同，这就是相差的分率与相差的量的区别。

基于儿童认知事物的特点，学生一年级学习数学时，最先接触的是数量。因为数是抽象的，而数量与生活相关，更接近学生的实际体验。上述教學过程中，教师通过提问“这两个条件一样吗？”调动学生思考，并紧扣这一核心问题，从学生熟悉的整数相差关系入手，帮助学生理解分数表示的相差的量也不变，再引导学生发现相差的分率和单位“1”有关，明确之前的经验不能进行简单的类推。

（二）从形似到神似：融演绎推理

小学生以形象思维为主要思考方式，在类比推理时容易因为追求形式的相似而忽略内在的联系，出现错误。因此，教师应适时融入演绎推理，通过演绎推理不断修正结论，从“形似”到“神似”。

例如，苏教版小学数学五年级上册《小数加法和减法》第一课时，学生会出现末尾对齐的错误算法，教师可以融合演绎推理开展教学：

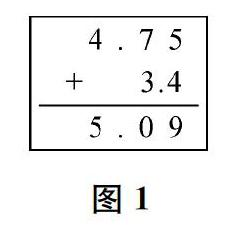
师（出示图1、图2）同学们出现了两种做法，左边是末尾对齐，右边是小数点对齐，请大家来说说对这两种做法的思考。

生第一种做法是错误的。4.75比4大，3.4比3大，结果一定比7大，所以5.09是错误的。

生4.75元是4元7角5分，3.4元是3元4角，合起来是8元1角5分，也就是8.15元，所以第二种正确。

师听了两位同学的回答，刚才用第一种做法的同学知道错在哪了吗？

（学生纷纷点头。）

师那请一位用第一种做法的同学来说说，为什么想到末尾对齐呢？

生整数475+34的竖式计算是末尾对齐，所以这里我也觉得是末尾对齐。

师看来是以前的学习经验对你产生了影响。（出示图3）我们一起来看，这里的两个式子都是末尾对齐，形式上相似，但形似了做法就相同吗？左边的式子表示什么？

生475个一加34个一是509个一，也就是509。

师再看右边，表示475个百分之一加34个十分之一，能直接加吗？

生不能，只有计数单位相同才能直接相加减，所以要将34个十分之一转化成340个百分之一，475个百分之一加340个百分之一是815个百分之一，也就是8.15。

生将34个十分之一转化成340个百分之一，计数单位相同才能直接相加减，这样就做到了数位对齐，数位对齐就是小数点对齐。

生从整数加减法到小数加减法虽然形式上发生了变化，但本质上都是数位对齐，这才是它们真正相同的部分。

师（出示图4）是啊，对齐的形式并不是它们真正相似的地方，数位对齐才是真正的神似。

从形似到神似，以演绎推理不断修正类比推理，使学生真正寻找到同化新知识的上位概念或相似概念，实现数学思维的正向迁移，从而深刻理解知识。

（三）从低阶到高阶：引深度思考

在帮助学生感知类比推理的或然性时，教师习惯用举反例的方法。确实，举反例能立刻击破学生类比推理得到的错误结论，但若仅仅如此，会让学生的思维停留在比较低阶的层次上。因此，还要在不断的辩证讨论中引发学生的深度思考，塑造学生的高阶思维。

例如，当学生根据长方形、正方形的面积公式推想到“平行四边形的面积=底×邻边”这一错误认知时，有教师会通过引导学生在方格纸上画平行四边形，应用数方格的方法，发现各种反例来明确错误。这样的教学设计看似简单高效，实则单薄浅显。可以开展如下的补充教学：

师同学们，我们已经学习了长方形、正方形的周长公式，你觉得平行四边形的周长公式应该是怎样的？

生我觉得和长方形、正方形一样，都是一组邻边的和再乘2。

生我赞同他的观點。可以做一个活动的平行四边形框架，拉伸后就成了长方形（或正方形），这个过程中周长不变，所以平行四边形和长方形的周长公式一样，都是一组邻边的和再乘2。

师看来，对于周长这个概念我们是可以把之前学习的长方形、正方形的经验直接迁移过来的。那平行四边形的面积呢？刚才我们通过在方格纸上举反例，明确了平行四边形的面积不是“底×邻边”。现在，你又有什么新的思考？可以结合刚才周长的研究过程小组探索一下。

（学生小组活动。）

生（展示图5）我们小组发现，将平行四边形拉伸成长方形，图中的涂色三角形可以平移到左边，将空缺补齐，上面斜线部分就是多出来的面积。

师也就说，拉伸后的长方形的面积比原来平行四边形的面积——

生（齐）大。

师这是因为——

生原来平行四边形的高变长了，所以面积变大了。

师如果将平行四边形往下压呢？

生面积会变小，因为它的高变短了。

生我发现，当平行四边形的底和邻边固定后，向上拉或者往下压就改变了高，面积也随之改变。所以不能用“底×邻边”来计算平行四边形的面积。

师周长可以类推，面积却不可以。长方形、正方形、平行四边形这三者之间的关系也太奇怪了！

生我觉得上面两个问题还要结合这三者之间的关系来理解。我们知道，长方形是特殊的平行四边形，正方形是特殊的长方形，（展示图6）它们三者的关系可以用这样的图来表示。正方形是特殊的长方形，所以长方形的周长和面积公式可以直接类推到正方形;而长方形是特殊的平行四边形，所以它的周长和面积的公式不能简单地类推到平行四边形。

生我赞同他的观点。周长研究的只是四条边长度的和，可以类推;但通过刚才的研究我们知道，平行四边形的面积与高有关，长方形和正方形一组邻边的夹角是90°，邻边就是高，而一般的平行四边形夹角小于90°，高和邻边不相等，所以不能类推。

根据布鲁姆认知目标分类，“回忆、理解、应用”为低阶思维，“分析、评价、创造”为高阶思维。确定“用‘底×邻边计算平行四边形的面积是错误的”对应学生的低阶思维，而要想让学生的思维向高阶发展，就需要引导其关注平行四边形一组邻边固定后高变化引起的面积变化，关注三类平面图形的关系，从而深化对三类图形周长和面积的认知。

类比推理作为合情推理的重要形式之一，在小学阶段有着广泛的应用，但其作为合情推理的或然性不容忽视。教师应引导学生重视其或然性并不断纠正偏误，养成有根有据的理性思维和实事求是的科学态度，锤炼良好的思维品质。

参考文献：

[1] 孙保华. 重视类比推理提升思维能力[J].教育科学论坛，2018（7）.