轴对称面源羽流运动特性的PIV实验研究

王 昕 宋冰岩 张玉洁 许宇坤 王 非

(上海理工大学环境与建筑学院 上海 200093)

热源羽流是普遍存在于日常生活与工作中的一种气流形态[1]，例如火灾产生的烟气、冷却塔排放的蒸汽、工业厂房设备散热引起的热羽流、汽车尾气、城市热岛等[2-6]。根据目前的研究成果可知，热源羽流会对环境流场造成一定程度的干扰作用，例如，厂房中不同类型的局部热源会产生浮力驱动的热羽流，不仅会破坏局部空调的稳定界面[7]，还会导致油雾及粉尘的扩散不受控[8]。但由于现阶段对羽流流场研究成果有限且不充分，在目前的实际工程通风系统设计中尚未涉及热源羽流对环境流场的影响[9]。因此，有必要进一步研究不同类型的羽流扩散运动及分布特性，为实际工程的通风系统设计提供理论参考。

已有研究在分析面源浮力羽流运动时，主要采取积分法[10]和虚拟点源法[11]，二者均以点源羽流理论为基础。上述两种方法得到的公式主要区别在于各系数的取值，这些系数主要通过对羽流实测数据进行幂指数形式的归纳而来，且系数的选取会较大程度影响对羽流运动的预测准确性。

测量羽流流场分布技术主要分为两类，即逐点测量和全局测量。逐点测量技术主要包括热线风速仪(HWA)[12]、热球风速仪(HAS)及超声波风速计(UA)[13]。大多数逐点风速计均为侵入式的设备，可能会导致局部气流的扰动，特别是在羽流速度较低的区域。且流场数据通常具有较低的空间分辨率，不足以识别复杂的室内流动特征。粒子图像测速(particle image velocimetry，PIV)作为一种新型全局流场速度测量工具，使用图像相关算法确定具有更高播种密度的速度矢量，可提供更高的信噪比和更高空间分辨率[14]，故本文选用2D-PIV作为测量热源羽流流场分布的实验方法，对目前常用的两种面源羽流速度与质量流量公式中的系数进行分析讨论。

本文利用大功率2D-PIV系统对不同热源强度、尺寸的面源羽流进行竖向区域测量，将测量区域在垂直方向上划分为3个小区域，通过3个小区域的测试数据进行拼接，获得全局流场分布。以此实测数据，对面源羽流的轴心速度、扩展半径公式进行系数讨论。

1 实验测试方法与误差分析

1.1 实验系统介绍

在带有独立温度控制系统的恒温恒湿实验舱内搭建高功率的2D-PIV系统，如图1所示。该系统由分辨率为2 048×2 048像素的TSI CCD照相机和最大分辨率为Beamtech Vlite500 Nd：Yag的激光器组成。将单一圆形热源水平置于地板上，热源由铸铝加热板制成，以产生面源热羽流。圆形热源的直径在10～25 cm之间，厚度为1 cm，如图2所示。热源由变压器控制加热功率，壁温(地板、侧壁、屋顶)和空气温度由恒温室恒温系统控制在13 ℃[6]。实验过程需要确保室内流场稳定且不受干扰，因此关闭了喷嘴送风与排风风阀且堵住了回风口。室内环境场达到稳定状态需要2 h。

图1 实验系统

图2 热源示意图

将大功率2D-PIV系统用于测量恒温室内圆形单一热源引起的热羽流，激光器发射的激光在532 nm的波长下脉冲能量为500 MJ。穿过TSI变焦镜头的激光束在测量区域产生厚度为1～3 mm的光片。TSI同步器向激光器和CCD摄像机发送信号，以使激光器的脉冲时间与摄像机的曝光时间相匹配，以确保它们的同步工作。

将密度为1.083 g/cm3的甘油作为示踪颗粒，粒子平均直径为约1.5 μm。利用PIV系统测量示踪粒子流场。测量时间为150 s，采样频率为1 Hz。结果表明，粒子在恒温密闭的室内扩散的最大速度为0.003 m/s，远低于热羽流的上升速度(约0.3 m/s)，故可认为颗粒与羽流流动具有很好的跟随性[15]。

受摄像机镜头和激光器性能的限制，测量时，将流场在垂直方向上分为3个子区域，每个子区域面积为350 mm×400 mm，如图3所示。每个区域样本总数为400，分为5个周期进行测量，每个周期连续测量80张快照。采样频率为3 Hz。由于CCD摄像机的分辨率有限且雾颗粒的散射效率有限，因此单次拍摄的最大视场(FOV)被限制为约0.14 m2。PIV图像分析是通过TSI INSIGHTTM 4G软件进行的。首先，采用去除背景的方式减少原始图像的背景图面误差。然后，使用快速傅立叶变换算法提取粒子图像中的速度矢量。通过自适应相关算法对这些图像进行处理，以获得每个子区域的时间平均流场，并且可以通过图像拼接获得全局流场。这些流场数据是以矩阵形式排列的矢量点，测量结果需要通过Tecplot 360软件进行进一步分析。询问窗口的最终大小设置为64×64像素，相邻子区域的重叠率为20%，所有FOV的空间分辨率为260 μm/像素。跨帧时间主要取决于最大气流速度和拍摄区域中的询问窗口大小。在此实验中，最佳横框架时间在最大流速为0.4 m/s时为1 000 μs，在0.25 m/s时为1 500 μs。

图3 流场横截面划分的子区域

1.2 误差分析

由于整个实验是在密闭的实验舱内完成，热源在加热过程中会对舱内温度环境造成影响，且面源热羽流是假定发热面温度均匀一致的条件下分析的，因此需要对实验过程中可能会产生的误差进行分析。在实验后分别对恒温室四周墙体及屋顶、室内空气进行温度测量采集，温度数据由安捷伦数据采集仪记录。以功率为100 W、直径为0.2 m的圆形热源为例，测量2 h内各测点的温度变化情况，如图4所示。结果表明：壁面及屋顶的温升在0.05～0.2 ℃之间，室内空气温升约在0.2 ℃。因此，认为热源的散热基本不会影响实验舱环境温度跃升。图5所示为热源表面温度的变化及分布均匀性。实验开始后的前30 min热源表面迅速升温，2 h后，热源表面温度基本稳定在65 ℃，且温度分布均匀。

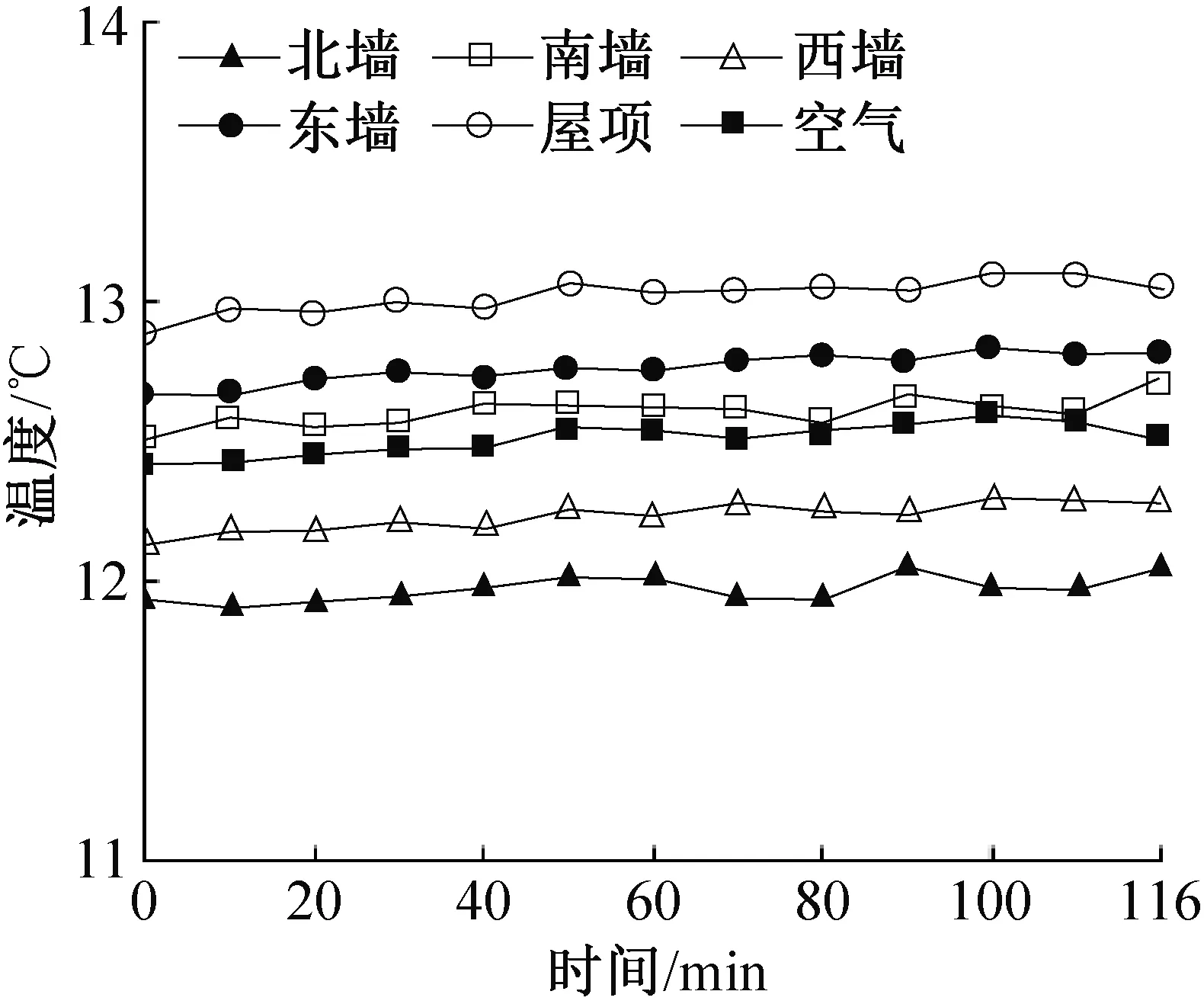
图4 恒温室各测点的温度变化

图5 热源表面温度变化及均匀性分布

文中将PIV测量误差分为系统误差和统计误差。系统误差是由多种因素引起的，例如播种浓度、粒子跟踪行为、背景噪声、图像失真、随机位移误差等。这些误差源不会独立影响系统精度。经过2D-PIV应用程序处理后，系统误差可控制在3%以内。PIV应用的统计误差主要是由随机抽样产生的。假设不相关的PIV数据的采样误差呈正态分布，则可以使用中心极限定理[16]评估标准随机采样误差。随机采样误差由式(1)、式(2)确定。

(1)

(2)

式中：S(U)为随机采样误差；Zα/2为与置信度相关的变量；N为样本数；U为局部空气速度，m/s；u′为局部空气速度的均方根。对于95%的置信度，0.4 m/s的空气速度，预估随机采样误差(250个样本)为9.3%～11.5%，绝对速度误差小于0.035 m/s。

2 实验结果

根据1.1节中介绍的测试方法，对16种不同尺寸、散热量的工况测试其羽流速度场，经过数据整理后获得完整流场数据，并根据中心坐标位置提取每个工况下流场的轴心速度，根据实验测量结果，尝试对谢比列夫通过积分建立的圆形面源羽流轴心速度式(3)[17]进行变形整合，得到不同参数下轴心速度与羽流高度的关系，定义如式(4)所式：

(3)

(4)

对式(4)中的散热量Q以及半径r进行系数修正。对于多系数的非线性曲线拟合，采用控制变量的方法确定未知系数。实验分别对半径为0.1 m且不同散热量(40、60、80、120 W)以及散热量为80 W且不同半径(0.050、0.075、0.100、0.125 m)的羽流轴心速度进行曲线拟合，分别如图6、图7所示。

图6 不同散热量时轴心速度随羽流高度的变化

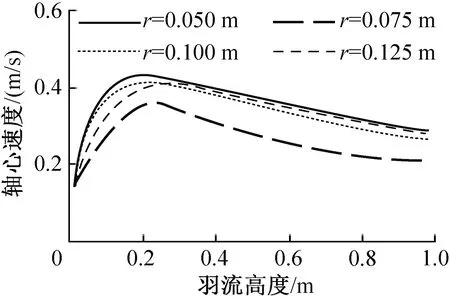
图7 不同尺寸热源中心线速度随羽流高度的变化

将图5、图6拟合系数a、b、c汇总至表1、表2中。由表1可知，热源散热量直接影响系数a的变化，而对系数b和c影响不显著。由表2可知，热源尺寸直接影响系数b、c的变化，而对系数a则影响不显著。系数a与散热量呈现出很强的线性关系，系数b、c与热源尺寸呈现出很强的线性关系。图8所示为3个系数的线性拟合结果，得到式(5)～式(7)，拟合度分别为0.999 6、0.999 2、0.997 2。

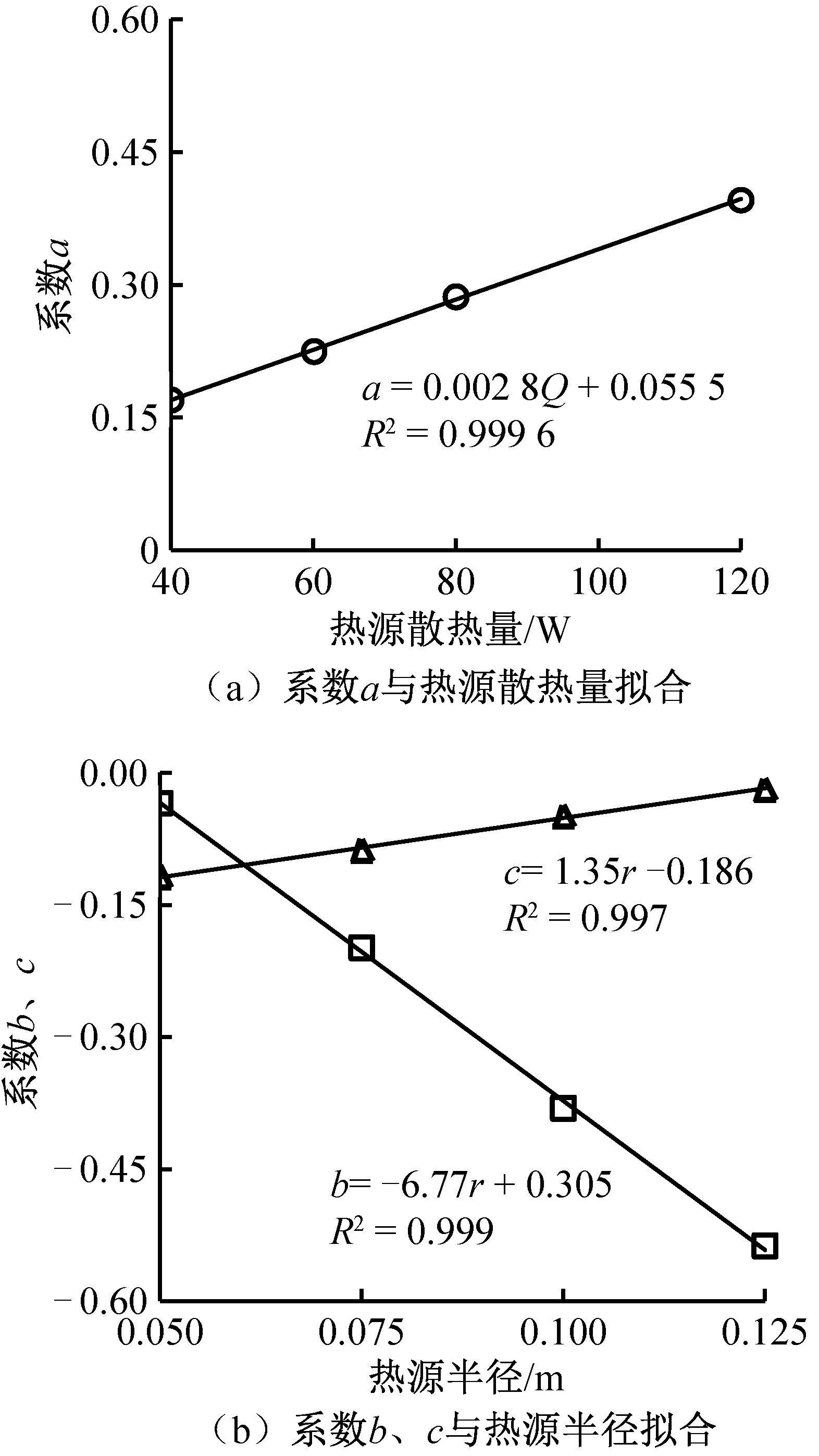
图8 轴心速度修正三系数的线性拟合

表1 不同散热量的拟合系数

表2 不同尺寸的拟合系数

a=0.002 8Q+0.055 5

(5)

b=-6.773 2r+0.304

(6)

c=1.346 4r-0.186

(7)

综合上述系数的拟合结果，轴心速度与羽流高度的关系修正如式(8)所示：

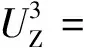
(8)

修正的公式中同一高度下影响轴心速度的因素只有热源尺寸与热源散热量，因此，为了进一步明确在相同高度下，热源尺寸与热源散热量对羽流轴心速度的影响，本文选取相同高度的实验数据进行拟合，如图9所示。

对于不同热源散热量与不同热源尺寸，选取同一高度下的实验数据，拟合后发现：热源散热量越大，相同高度下的热羽流速度越高，热源尺寸越小，相同高度下热羽流速度越高；且相比于热源半径对羽流速度的影响，散热量对羽流速度的影响较大。

3 结论

本文根据羽流运动特征，利用焓差实验室及大尺寸2D-PIV系统，对单个圆形热源4种不同尺寸(r=0.050～0.125 m)及4种不同散热量(40～120 W)共16种工况下产生的羽流流场进行测试，通过同步移动相机及激光器扩大了测量范围，测得较完整的羽流流场。将测得的数据提取轴心速度并对比分析，得到如下结论：

1)得到一个更简便且较为准确的圆形面源羽流轴心速度表达式(式(5))，并对式中的系数进行拟合修正，在热源半径为0.050～0.125 m，热源散热量为40～120 W之间能够较好的反映出热羽流轴心速度随远离热源高度的变化关系。

2)热源散热量在40～120 W之间，半径在0.050～0.125 m之间，热源尺寸的变化不影响羽流的扩展趋势，仅影响扩展半径的初始值。

3)在实验条件下，距离热源同一高度，热源散热量越大，热羽流速度越高；热源尺寸越小，热羽流速度越高；且相比于热源半径对羽流速度的影响，散热量对羽流速度的影响较大。

本文受上海市自然科学基金项目(16ZR1423200)，机械行业创新平台项目(2019SA-10-07)和山东省建设厅开发项目(K2019370)资助。(The project was supported by the Natural Science Foundation of Shanghai(No.16ZR1423200), Machinery Industry Innovation Platform Construction Project(No.2019SA-10-07), and Shandong Construction Department Research and Development Project(No.K2019370).)