筒型翅片管换热器空气侧换热模型分析与实验

黄 楚 谷 波 田 镇 沙宇雄

(1 上海交通大学制冷与低温工程研究所 上海 200240；2 上海海事大学商船学院 上海 201306)

筒型组合式空调机组是一种新型高效空调末端装置，机组的换热器采用特制的断面为圆形的筒型翅片管换热器。作为制冷设备中的核心换热部件，筒型翅片管换热器与传统翅片管换热器相比具有漏风率低、空气侧阻力小、占用空间小的明显优势[1]。

筒型换热器的技术核心是实现了过渡季节高效而简单的空气旁通：工作季节时，出口风阀关闭，空气到达风阀后向四周横向扩散并通过换热器，实现高效换热；过渡季节时，出口风阀打开，空气直接从换热器轴向通过，而不经过换热器，风阻极低，因此大幅减小了过渡季节为克服换热器阻力而浪费的功耗，起到节能的效果。

在筒型翅片管换热器的换热过程中，空气侧热阻占总热阻的主要部分，因此建立准确的空气侧换热模型不仅对筒型翅片管换热器的强化换热研究具有重要的理论意义，同时对筒型翅片管换热器的结构设计与性能分析也具有实际应用价值。

目前，针对翅片管换热器的空气侧换热研究主要集中于建立更加精确的空气侧换热的预测模型，以及研究影响换热效果的换热器结构参数，且研究对象多为传统形式的翅片管换热器。D.T.Beecher等[2]完成了最早的人字形波纹片式翅片管换热器的研究，R.L.Webb等[3-4]对Beecher的实验重新编排并提出了关联式结果，但提出的关联式未充分考虑可能产生影响的结构参数，导致关联式虽然能够对其论文中的实验数据较好拟合，但对于新的实验数据泛化能力较差。为了得到涵盖范围更广的关联式，C.C.Wang等[5-9]进行了充分变工况、变结构、变翅片形式的换热器实验，关联式结果得到业界的广泛认可，能够适用大范围的换热因子j与摩擦因子f的预测。B.Youn等[10]在总结前人实验结果的基础上，进行了不同结构正弦波纹片的实验，提出了适用于正弦波纹的实验关联式。Ma Xiaokui等[11]对多种翅片形式换热器进行了研究，得到三角波纹片与间断式翅片在湿工况下的传热与阻力实验关联式。

通过实验数据修正已有关联式来预测不同工况与不同结构的换热器性能，也是常用的方法。谷波等[12]针对正弦波纹形式的翅片管换热器的空气侧传热进行了进一步研究，对原有关联式系数进行了修正。梁斌等[13]在原公式基础上，推导出低气压条件下的换热器显热与潜热的换热公式。

对于筒型翅片管换热器，由于其特殊的风路结构，各排的风侧参数呈非线性变化，导致空气侧传热特性明显区别于传统翅片管换热器，目前针对筒型翅片管换热器的相关研究还处于起步阶段。曾炜杰等[1,14]提出一种各排间换热模型采用集总参数法，逐排参数传递的分排参数换热模型，并对比分析了筒型翅片管换热器与传统换热器的性能，彭文豪等[15]以单排换热管为单元，研究了对单排换热管进行迭代求解时出现的收敛性问题。

目前尚无圆筒结构的翅片管换热器空气侧换热模型的研究。本文针对筒型翅片管换热器与传统翅片管换热器的结构特点，对换热模型进行了理论分析，基于现有翅片管换热器数值模型中的空气侧关联式，提出一种通用于传统结构与筒型结构的翅片管换热器空气侧关联式，最后通过多组变工况、变结构的实验对式中的相关系数进行修正，得到了具有更加普适应用价值的实验关联式。

1 筒型换热器空气侧换热理论分析

1.1 现有空气侧换热关联式总结

本文总结了几种当前认可度较高的空气侧换热特性的理论预测模型，如表1所示。由于本文研究的筒型翅片管换热器对象为正弦波纹形式，因此将主要基于关联式1进行系数修正。

表1 各关联式形式及引用来源

1.2 筒型换热器中翅片间距及风速变化规律

筒型翅片管换热器原理如图2所示。筒型翅片管换热器与传统换热器的最大区别在于，各排翅片间距沿气流方向逐渐增大，导致各排的流通面积不同，从而使各排的平均风速与最大风速均不同。

图1 圆筒型空调机组与筒型翅片管换热器

图2 筒型翅片管换热器原理

筒型翅片管换热器的主要结构参数定义如图3所示。在筒型翅片管换热器中，定义中心片距Fp为靠近圆心侧的翅片端点的间距，即最小圆弧圈处的翅片间距大小；约定靠近圆心的最内圈管排序号为1，管排序号向外依次增大。最小圆弧的半径与第一排管圆弧半径相差半个沿气流方向管排距。根据几何相似性可以得到各排管翅片间距与管排序号的关系如式(1)所示。

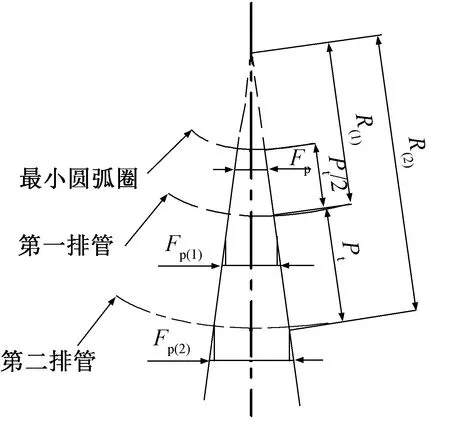
图3 筒型翅片管换热器结构

(1)

由式(1)可知，在筒型换热器中，各排翅片间距大小Fp(n)与中心片距Fp、最内圈半径R(1)、沿气流方向管排距Pt、所在管排序号n均相关。

各排的最大风速与换热器体积风量、最小流通面积Smin有关，而Smin随管排数序号增加，呈非线性变化；同时空气在热湿交换过程中的密度不断改变，导致最大风速变化规律复杂。以三角波纹换热器(结构参数：Fp=3.1 mm，Dc=12.70 mm，N=6，Pl=27.5 mm，垂直排数16排，圆弧度角316°，回路形式为半回路)为例，实验工况为：循环风量8 024 m3/h，进风干、湿球温度分别为28.53 ℃和22.98 ℃，进水温度为6.95 ℃，水质量流量为10 149.85 kg/h。

各排迎面风速和最大风速随管排位置的变化如图4所示。

图4 各排管迎面风速与最大风速

由图4可知，迎面风速随所在管排的序号改变变化相对平缓，且基本呈线性变化。这是由于迎面风速主要与迎风面积相关，而迎风面积大小与各排换热管圆弧直径成正比，因此迎风面积也近似成正比关系；而最大风速的变化更为剧烈，且不符合线性变化规律。因此，雷诺数的变化将变得更为复杂，Re对换热性能的影响也呈现新的规律。

综上所述，筒型换热器的空气侧换热与传统方形换热器具有不同特点，传统结构的空气侧关联式不适用于筒型结构，针对筒型换热器结构，开发新的实验关联式具有重要意义。应对原有公式形式进行修正，修正后的关联式应能够反映各排直径变化、翅片间距变化等因素对换热性能的影响。

2 实验设计

2.1 实验对象与工况

为了研究筒型翅片管换热器的结构参数对空气侧换热因子的影响，本文对3种具有不同内外圈直径的筒型翅片管换热器以及1种传统形式的翅片管换热器进行了共计33组变工况实验，换热器的波纹形式均为正弦波纹，实验工况测试范围如表2所示，样品参数如表3所示(所有样品的相同尺寸参数为：Dc=12.70 mm，Pt=31.75 mm，Pl=27.5 mm，N=4)。其中，传统换热器的内圈直径是指单排管的长度。

表2 实验工况范围

表3 波纹翅片管换热器结构尺寸

2.2 实验系统设计

实验对象为大型换热器，实验主要在大型焓差实验室中完成，大型换热器将会造成实验台负荷较大，因此需要水系统提供足够冷量，采用水冷式冷水机组供冷。水温由冷水机组、高温热泵机组与管路电加热设备协同控制，主要通过三通阀的开度，实现初步的水温控制；同时使用管路中加热器对水温微调，实现更加精确的控温，水系统原理如图5所示。

图5 水系统原理

环境室的部分主要包括环境间、工况间、风量测量装置等设备，环境室内分为上下两层，下层功能设备主要包括均流器、喷嘴、取风样机、风机等；上层功能设备主要包括过滤器、表冷器、热湿精准控制等。空气首先在工况间进行热湿处理，由压缩冷凝机组的冷热盘管提供冷、热量，之后风道内的电加热进行精确温控，最后电加热、电加湿设备调节湿球温度。处理后的空气满足实验要求的进风状态，由变频风机引入环境室，进入换热器进行测试。环境室原理如图6所示。

1进风取样器；2、8、13 RTD(Pt100Ω)；3取样风机(进风)；4变频风机；5换热器样品；6出水管路；7进水管路；9水系统；10压力变送器；11均流器；12出风取样器；14取样风机(出风)；15压差变送器；16喷嘴室；17辅助引风机；18旁通风阀；19表冷加热盘管；20电加热/加湿；21变频风机；22吊顶冷风机。

2.3 实验数据处理

所有实验数据通过安捷伦数据采集仪34972A获得；设备启停、工况设定及所有数据的采集计算工作，均在监控电脑上进行。

为保证测量结果的准确性，每组实验数据均在流动稳定后在等时间间隔下测量7次，取平均作为该组工况的测量结果，各参数的测试精度如表4所示。

表4 实验参数测试精度

实验数据采用对数温差的LMTD处理法，关键处理步骤如下：

1)取实验测得的空气侧换热量与水侧换热量的算术平均值，作为系统的实际换热量：

(2)

2)根据热阻计算方程，得到总换热量与水侧、空气侧传热系数的关系，由于管壁导热热阻远小于水侧与空气侧，为简化计算忽略此项：

Qm=UAΔT

(3)

(4)

ΔT=φ(ΔTm)ctf

(5)

3)采用Gnielinski关联式[16]计算水侧传热系数：

(6)

fi=[1.58ln(ReDi)-3.28]-2

(7)

4)假设空气侧传热系数初值，通过迭代直至空气侧显热的两种计算方法结果差异小于一极小值ε，则判定为收敛：

Q1=Gacp,a(Ta,out-Ta,in)

(8)

Q2=hoAoηo(To,m-To,sur)

(9)

(10)

迭代至|Q1-Q2|<ε时，结束。

5)根据迭代得到的传热系数，使用Colburn换热因子j来表征空气侧换热性能：

(11)

3 实验结果分析

3.1 换热因子与雷诺数变化趋势

筒型与传统换热器的空气侧换热因子j与空气侧最窄流通面的Re关系如图7所示，图中筒型翅片管换热器为表4中的样品2，传统换热器为样品4。实验发现两者的j均随着Re的增大而减小，且Re较低时，Re变化对j影响较大；Re较高时，Re变化对j影响逐渐减小。这与Wang C.C.等[5-9]的实验结果一致，说明筒型翅片管换热器的j随Re的变化趋势与传统换热器相同。

图7 换热因子j实验值与空气侧最窄流通面Re的关系

3.2 现有关联式的适用性分析

已有的空气侧换热因子关联式的研究均是针对传统换热器，未考虑筒型翅片管换热器各排最大风速与Re非线性变化，因此将不适用于筒型翅片管换热器。

图8所示为实验测得换热因子与表1中关联式1预测换热因子的误差对比。由图8可知，关联式1对于传统形式的换热器拟合度较好，误差均在0～10%的误差区间，平均误差为7.53%，最大误差仅为8.75%，证明了实验数据的合理性以及关联式1的可靠性。

图8 现有关联式换热因子j预测值与实验值对比

而对于筒型翅片管换热器，关联式1的预测值误差全部在30%以上，所有筒型翅片管换热器的平均误差为81.16%，最大误差达到了133.99%，且预测值均高于实验值。这是因为传统换热器的预测关联式未考虑筒型翅片管换热器各排风速变化对换热带来的影响，直接使用空气侧最窄流通面的Re代入关联式。由于圆筒换热器的风速、Re由内至外逐排递减，实际的整体平均Re会低于空气侧最窄流通面的Re，从而造成巨大的误差，因此传统换热器模型不适用于筒型翅片管换热器。

3.3 筒型换热器实验关联式开发

以表1中列举的关联式1[10]为例，该学者研究发现影响空气侧换热的主要结构参数为：雷诺数、沿气流方向管间距、垂直气流方向管间距、翅片间距、管外径、翅片形状这6个因素。筒型翅片管换热器由于其特殊结构，雷诺数与翅片间距项是存在变化的，各排风速也呈现非线性变化，难以直接代入公式。

换热器结构如图9所示。考虑筒型翅片管换热器的结构特点，各排直径逐排向外增大，翅片间距也逐渐增大，若将筒型翅片管换热器的各管排拉直，可以将筒型翅片管换热器视为一种梯形管排的换热器，有效长度沿气流方向逐排增大。传统翅片管换热器也可以看做是一种特殊的内圈直径趋于无穷大的筒型翅片管换热器，所以在拉直后，沿气流方向的有效长度和翅片间距也几乎无变化。因此，合理的筒型空气侧性能预测关联式，也适用于传统结构。

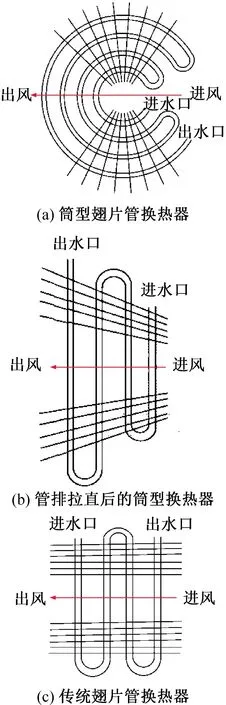
图9 换热器结构

针对正弦波纹的筒型翅片管换热器，本文在表1中关联式1的基础上，提出一种用最内圈翅片间距Fp(1)与最外圈翅片间距Fp(N)的算数平均值Fp,mid代替原关联式中翅片间距，并对Re的幂增加了表征筒型翅片管换热器拉直后的梯形倾斜程度的修正因子。

修正后得到的筒型翅片管换热器空气侧换热新关联式形式为：

(12)

(13)

式中：C1～C6为常系数；Fp,mid为最内圈与最外圈翅片间距的算数平均值，Fp,mid=(Fp(1)+Fp(N))/2；(D(N)/D(1))为最外圈与最内圈直径之比；(Pt/D(1))为排距与最内圈直径之比。

传统形式换热器可视为一种特殊的筒型翅片管换热器，其内圈直径D(1)趋近于正无穷∞，此时：

(14)

(15)

Fp,mid≈Fp

(16)

将式(14)～式(16)的化简值代回关联式式(12)、式(13)，发现修正因子约掉后，关联式与修正前的形式一致，因此也能正确对传统换热器进行预测。

3.4 关联式系数拟合结果

利用本文得到的实验数据，对3.3节中提出的筒型翅片管换热器关联式(12)、关联式(13)中的新增系数C1～C6进行拟合，得到新的关联式：

(17)

(18)

图10所示为利用实验数据重新拟合的新关联式的换热因子j的预测对比，与图8对比可知，修正后关联式的预测精度大幅提升，±20%误差区间的数据占93.75%，且误差分布均匀，平均误差为8.86%，最大误差为25.47%。

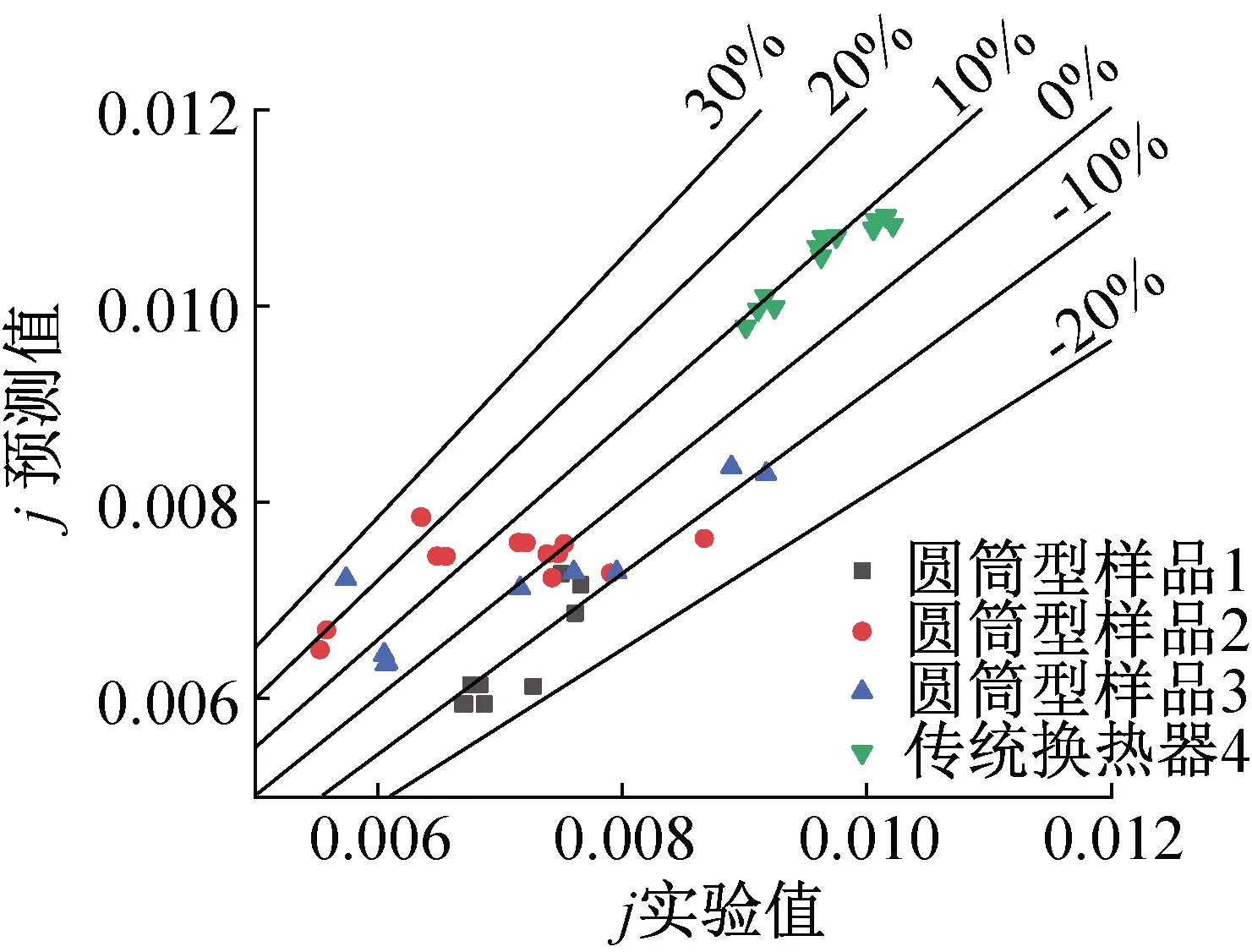
图10 新关联式换热因子j预测值与实验值对比

新关联式与原关联式预测的各样品误差对比如表5所示。针对3个圆筒型样品，新关联式的平均误差分别为13.13%、7.49%、7.20%；原关联式的平均误差分别为85.78%、83.96%、74.31%，由此可知，新关联式对筒型换热器的预测精度更高。

表5 修正后关联式的预测偏差

如1.3节中所述，该关联式也能较好地预测传统形式换热器，把传统换热器视为一种特殊的内圈直径D(1)趋于无穷大的筒型翅片管换热器，关联式将退化为修正前的形式。新关联式对传统换热器样品4的平均误差为8.80%，与原关联式平均误差7.53%相比没有明显劣势。因此，本文提出的关联式不但能更好的适用于筒型翅片管换热器，也保持了对传统翅片管换热器的预测精度。

4 结论

本文针对筒型翅片管换热器空气侧流动与风速分布的特点进行了理论分析与实验验证，基于目前预测精度相对较好且认可度较高的传统翅片管换热器的空气侧换热模型，提出了一种能反映筒型翅片管换热器结构参数特点、同时又涵盖筒型翅片管换热器与传统翅片管换热器的新通用关联式形式，并针对筒型翅片管换热器进行了多组变结构、变工况的实验分析。得到如下结论：

1)筒型翅片管换热器的空气侧换热因子j随Re的变化趋势与传统换热器相同，j随Re的增大而减小；且Re较低时，Re变化对j的影响较大；Re较高时，Re变化对j影响逐渐减小。

2)使用现有的关联式预测筒型翅片管换热器的换热因子，平均误差达到81.16%，最大误差达到133.99%，这是因为传统关联式无法反映圆筒换热器各排参数差异，因而不适用于筒型翅片管换热器。

3)本文修正后的新关联式对筒型结构的翅片管换热器的实验数据有较好预测，平均相对误差为8.86%，且误差分布均匀，大幅提高了换热模型对筒型翅片管换热器的适用性，同时也保持了关联式对传统翅片管换热器空气侧换热的预测精度。

符号说明

j——Colburn换热因子

Re——雷诺数

s——翅片间距，m

Dc——包含翅片厚度的管外径，m

Dh——水力直径，m

R——管排圆弧半径，m

D——管排圆弧直径，m

Xf——翅片波纹的投影长度，m

Pt——沿气流方向排距，m

Pl——垂直气流方向排距，m

Pd——翅片波纹的波峰到波谷高度差，m

N——沿气流方向总管排数

Sf——翅片间距，m

Le——换热器有效长度，m

U——换热器总传热系数，W/(m2·K)

A——换热器的传热面积，m2

T——温度，K

ΔT——逆流交叉形式对数温差，K

(ΔTm)ctf——换热器内冷热流体逆流布置时的对数平均温差，K

ηo——整体翅片效率

η——翅片效率

h——对流换热表面传热系数，W/(m2·K)

Pr——普朗特数

f——阻力系数

G——质量流通流量，kg/s

cp——定压比热容，J/(kg·K)

K——传热系数，W/(m·K)

Fp——最内侧翅片间距，m

n——沿气流方向第n排管序号

Fp(n)——第n排管的翅片间距，m

R(1)——第一排管的圆弧半径，m

Q——换热量，W

φ——温差修正系数

下标

a——空气侧

w——水侧

m——算术平均

i——管内

o——管外

f——翅片

in——入口

out——出口

sur——翅片表面