噪声和振动等舒适度曲线的快速确定方法

刘李娜，黄 煜，龚楚楚，李 喆，何 颖

（1.中国人民解放军海军特色医学中心，上海200433；2.上海交通大学 机械与动力工程学院 机械系统与振动国家重点实验室，上海200240）

噪声和振动是车辆、船舶和飞机等交通工具舱室内部影响人体舒适性的重要因素。现有研究大多基于客观测量和主观评价，通过分析客观物理特征和主观心理指标之间的关系，最终建立不同环境中噪声或振动的不舒适度（烦恼度）预测模型[1-10]。由于在舱室内部环境中，人们往往同时暴露于噪声和振动中，因此可以用同一指标（如不舒适度）来统一量化噪声和振动对人体舒适性的影响。

根据Stevens’power law，噪声和振动的不舒适度主观幅值ψs和ψv可以通过幂函数用两者的客观幅值φs和φv描述，即：

其中：ks、kv、ns和nv均为常数，ns和nv分别表示噪声和振动不舒适度随客观幅值的增长率[11]。令ψs=ψv，即可得到噪声和振动的等舒适度曲线。该曲线描述了噪声和振动各自对人体舒适性影响的相对重要性，对噪声振动控制中减振或降噪的优先级起指导作用。

要确定噪声和振动的等舒适度曲线，通常需要进行完整的交叉感觉主观评价实验，获取所有幅值噪声激励相对于所有幅值振动激励的不舒适度，以及所有幅值振动激励相对于所有幅值噪声激励的不舒适度，再将它们表示在横、纵坐标分别为噪声和振动客观幅值的坐标系中。以声暴露级（SEL）和振动剂量值（VDV）为例，当φs=LAE，φv=aVDV，令ψs=ψv，则得：

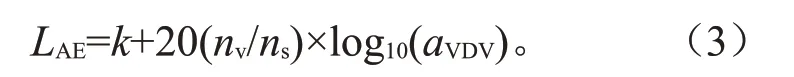
式（3）表示在对数坐标系下，噪声和振动的等舒适度曲线是一条斜率s=20(nv/ns)的直线[12]。

完整的交叉感觉实验往往需要较长的时间和工作量。根据式（3），噪声和振动的等舒适度曲线的斜率可以由nv和ns的比值得到，而增长率ns和nv可以通过噪声或振动的主观评价实验获得。那么，是否可以不进行完整的交叉感觉实验，仅通过一组噪声和振动的主观评价分别获得ns和nv，再通过式（3）确定二者的等舒适度曲线？目前为止，鲜有文献对此给出明确回答。

本文拟在之前工作的基础上[13]，通过主观评价实验，进一步研究噪声和振动等舒适度曲线的快速确定方法：即在相同的实验条件下，直接通过计算ns（即噪声不舒适度随SEL的增长率）和nv（即振动不舒适度随加速度的增长率）的比值，确定噪声和振动等舒适度曲线的斜率，最终确定噪声和振动的等舒适度曲线。

图1 噪声（A计权）和振动激励样本（Wk计权）时域和频域图

1 方法

1.1 激励

同步测量和记录汽车内部的噪声和振动。前排乘客座椅表面垂向加速度通过座垫加速度传感器（Brüel &Kjær，丹麦，型号4515B）采集。座垫与水平面的夹角约25度，座垫传感器固定于乘客坐骨结节之间的正下方。前排乘客的双耳噪声通过人工头（HEAD Acoustics，德国，型号HMS IV）采集。采集到的噪声和振动信号通过Müller-BBM PAK 噪声振动测试分析系统（Müller-BBM，德国，型号PAK MKII，版本V5.7）同步记录。

选择沥青路上车辆以40 m/h行驶时的噪声和振动信号作为原始激励样本，样本时长为4 s。噪声样本的A 计权SPL是65 dB(A)[14]。振动样本的Wk计权加速度值为0.32 m/s2[15]。在样本的起始和结束处分别加上长度为0.2 s的余弦衰减包络后，其时域和频谱如图1所示。基于激励样本的频谱调整幅值，生成10个SEL 幅值范围从64 dB(A)到91 dB(A)、间隔为3 dB的噪声激励；生成10个VDV 幅值范围从0.11 m/s1.75到1.1 m/s1.75、间隔为0.11 m/s1.75的振动激励。

1.2 受测者信息

选取12个上海交通大学的男学生作为实验的志愿受测者，其年龄中值为28岁（25岁到30岁），身高中值为172 cm（164 cm到178 cm），体重中值为67 kg（56 kg到90 kg）。所有受测者在参与实验前都正式签署了同意文件。

1.3 实验装置

实验在电磁振动台（LDS，英国，型号V8-640T LPT1220/SPA56K）的900×900 mm的垂直振动铝合金平台上进行。自制铝合金座椅通过刚性连接固定在该垂直振动台上。受测者端坐在座椅上，背部不接触座椅靠背，双脚平放于振动台上，如图2所示。

图2 实验装置图

振动台通过LMS SCADASIII 控制系统（SIEMENS，德国，型号SC310）控制。在座椅座垫下方放置一个压电式加速度传感器（厚德自动化仪表，中国无锡，型号HD-YD-216）实时监控测量垂向加速度。振动信号通过LMS Test Lab 产生，采样频率为512 Hz。

噪声激励通过Adobe Audition CS6（Adobe Systems，美国）产生和控制，经由MAYA44 USB2.0音频界面（ESI Audiotechnik，德国）输出至受测者佩戴的耳塞（Etymotic er4p）。受测者同时佩戴一副隔音耳罩（3M 1425），以减小振动台运行时背景噪声的干扰。隔音耳罩隔音效果约为20 dB，插入式耳塞的隔音效果约为25 dB。噪声激励通过人工头（HEAD HMS IV，配套软件ArtimiS SUITE）进行校准：人工头佩戴耳塞，通过回放设备调整输出值，使人工头接收到的噪声激励的声级等于实验设置值，即SEL范围为64 dB(A)到91 dB(A)，间隔3 dB。通过声级计（Brüel&Kjær Type 2250）现场测量得到，振动台运行时的背景噪声SPL约为75 dB(A)。

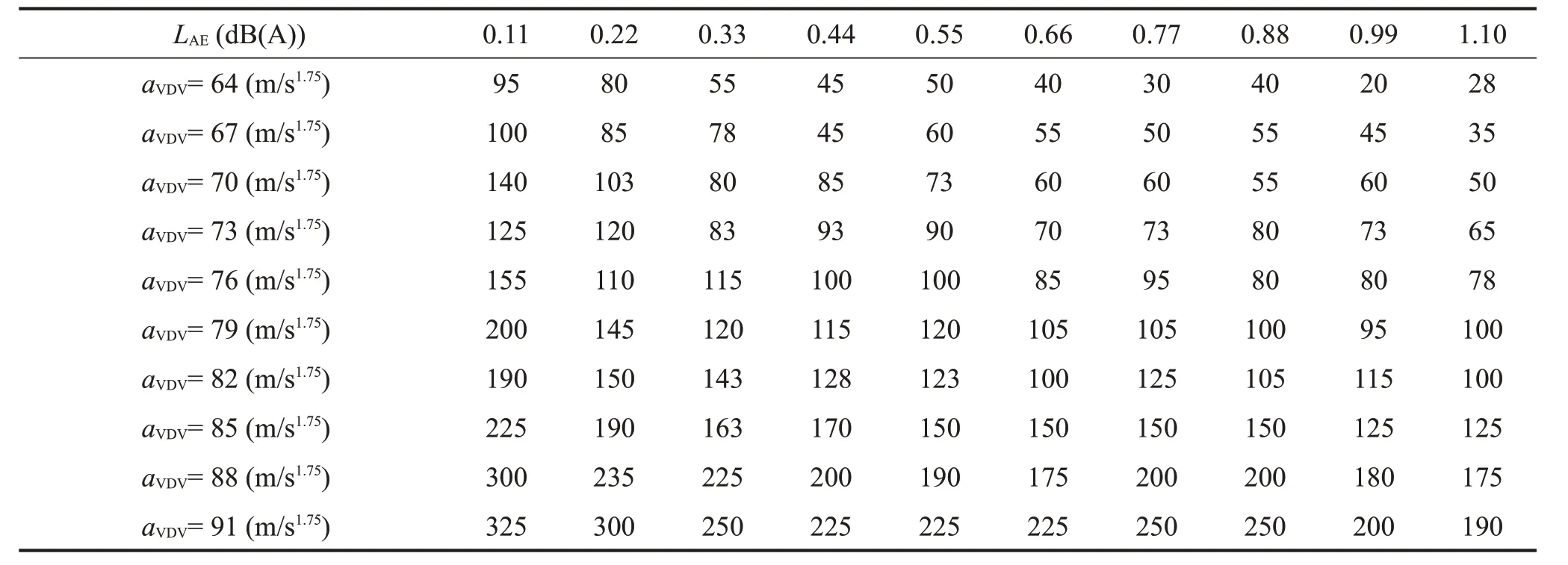
表1 受测者群体的噪声不舒适度评价中值

1.4 实验步骤

受测者运用相对幅值评价法[12]对噪声或振动产生的不舒适度进行评价。实验分成A和B两部分进行。A部分实验，每个受测者随机经历10个噪声激励跟10个不同幅度振动激励的组合，共计100 对。要求受测者在经历每一对噪声和振动的组合之后，以振动为参考激励，假设其不舒适度为100，给出噪声产生的不舒适度值。B部分实验，每个受测者随机经历10个振动激励和76 dB(A)的噪声激励的组合。要求受测者在经历每一对噪声和振动的组合之后，以76 dB(A)的噪声激励为参考，假设噪声产生的不舒适度值是100，给出振动产生的不舒适度值。一半受测者先参加A部分，再参加B部分；另一半则反之。

受测者在正式开始实验之前，首先阅读实验说明，大致了解自己需要完成的任务；然后通过判断线条长度进行幅值评价法的练习，再在振动台上随机尝试判断较小、中等或较大幅值激励的不舒适度。当受测者熟悉实验流程之后，实验正式开始。

2 结果

2.1 噪声相对于参考振动的不舒适度

受测者群体的噪声不舒适度主观评价值中值如表1所示。表中每一个参考振动激励的不舒适度值均为100。

从式（1）知，噪声不舒适度值ψs同SEL在对数坐标轴上可以表示为

其中：LAEμ20 log(φs)是A计权的等效连续SEL值，假设φs为声压[12,14]。对表1中每个参考振动激励下的因变量log10(ψs)和自变量LAE作线性回归分析，得到截距、斜率和相关系数，如表2所示。同时将ψs=100代入线性回归曲线，算出同参考振动激励具有相同的不舒适度值的SEL，见表2的LAE列。

表2 不舒适度值log10(ψs)相对于LAE的线性回归分析

根据式（3），将表2中的LAE列和aVDV列中的数据作线性回归，得到噪声和振动产生的不舒适度等效曲线，相关系数为0.958：

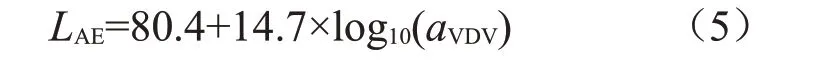
2.2 振动相对于参考噪声的不舒适度

从式（2）知，振动不舒适度值ψv同VDV 在对数坐标轴上可以表示为

式中：φs即VDV值。

受测者群体的振动不舒适度主观评价值中值如表3所示。此时不舒适度100的参考噪声的SEL为76 dB(A)。对因变量log10(ψv)和自变量log10(aVDV)作线性回归，得到截距、斜率和相关系数，列于表3第3列。

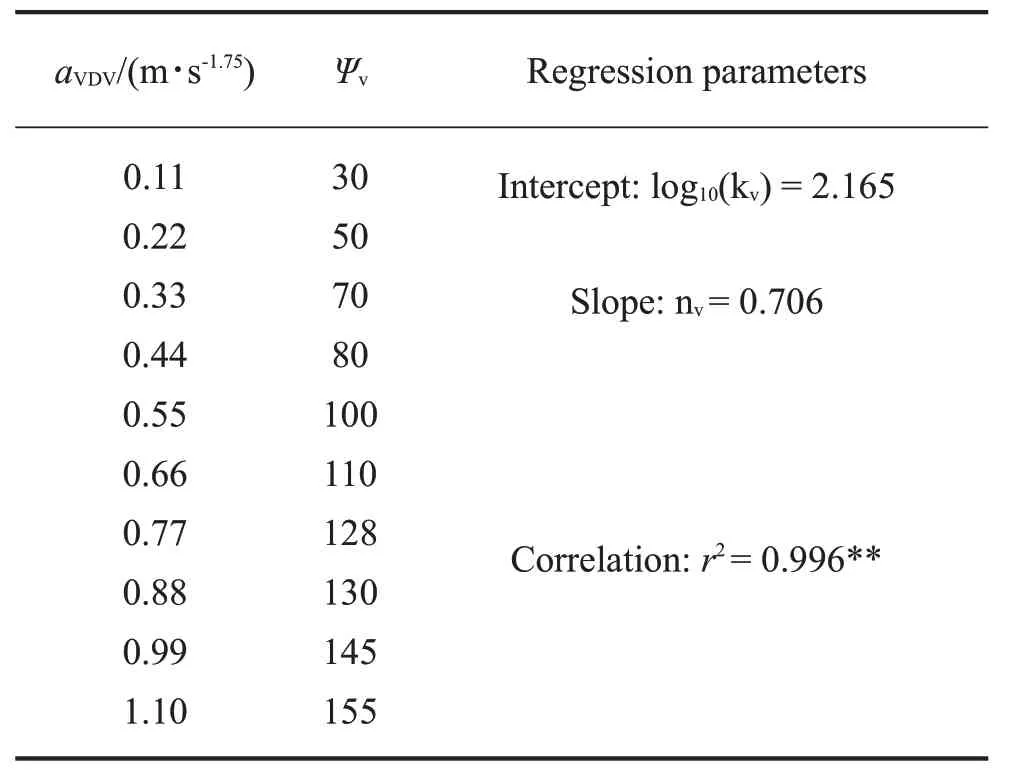
表3 受测者群体的振动不舒适度评价中值和线性回归参数

2.3 基于不完整交叉评价的等舒适度曲线

从表3中的线性回归参数（即截距log10(kv)和斜率nv）可知，VDV是0.58 m/s1.75的振动不舒适度与SEL是76 dB(A)的噪声不舒适度相等，即log10(ψv)=100。利用0.58 m/s1.75和76 dB(A)以及表2中产生相等不舒适度的LAE和aVDV，可以得到噪声和振动的等舒适度曲线。例如，从表2中选取78.6 dB(A)的噪声与0.77 m/s1.75的振动，结合表3中的76 dB(A)的噪声和0.58 m/s1.75的振动，即可通过线性方程计算获得噪声和振动之间的等舒适度曲线。

尝试将表2和表3中的不同SEL 和VDV组合，得到噪声和振动的多条等舒适度曲线，结果如表4所示。表2.4 中每一行的斜率和截距都是根据表2中对应的LAE和aVDV（同表2.2）结合表3中的0.58 m/s1.75和76 dB(A)计算得到。

表4 噪声和振动的等舒适度曲线

另一方面，根据s=20(nv/ns)，等效曲线斜率也可以通过ns和nv的比值得到。表2.2 中ns/20的值从0.019到0.036（中值是0.027），表3中nv=0.076，因此等效曲线斜率值的范围从19.6到37.2（中值是26.1）。

3 讨论

3.1 不同研究中的等舒适度曲线对比

Huang和Griffin比较了前人研究中不同的噪声和振动的等舒适度曲线，并解释了两类分歧产生的原因[12]。图3中比较了根据不同研究[12，6-20]得到的噪声和振动等舒适度曲线，包括本实验A部分（噪声相对于参考振动激励的不舒适度）。图3的坐标范围为实验中VDV的取值范围（Paulsen的曲线基于速度均方根值[20]）。等舒适度曲线的不同斜率值取决于实验中受测者关注噪声或者关注振动，即实验中是噪声主导或振动主导[12]。在本实验A部分、Hempstock 等的实验[17]、Paulsen 等的实验[20]以及Huang 和Griffin的实验A部分[12]，噪声是感觉主导量（受测者评价噪声，参考激励是振动），因此得到相近的等舒适度曲线斜率。Paulsen 和Kastka的等效曲线截距同本实验中得到的截距差别较大，原因可能是Paulsen的实验中背景噪声和噪声激励的幅值低于本实验，而振动激励的幅值跟本实验相近。本研究结果同Hempstock以及Huang 和Griffin得到的等舒适度曲线较吻合，并将曲线的有效预测范围下限从0.1 m/s1.75VDV拓展至0.05 m/s1.75VDV。

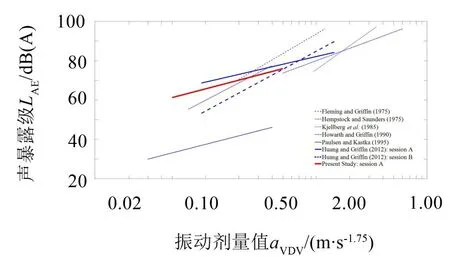
图3 不同实验中噪声和振动的等舒适度曲线

3.2 噪声和振动的相互影响

从表2可知，当参考振动激励的幅度从0.11 m/s1.75增加到1.10 m/s1.75，噪声不舒适度随客观幅值变化的斜率ns/20 从0.019 增加到0.036，跟Huang 和Griffin的斜率变化（从0.02到0.028）[12]大体一致；而学者普遍接受的由Stevens[11]建议的斜率值大约是0.33。斜率值随参考激励增大而变大的主要原因可能是噪声和振动相互之间的“掩蔽效应”，较大幅值的振动掩蔽了较小幅值的噪声产生的不舒适度，使得受测者对幅值较小的噪声倾向于给出较小的不舒适度评价值；而较大幅值的噪声受振动的影响较小。因此，同较大幅值的振动组合的噪声不舒适度随幅值的增长率ns大于同较小幅度的振动组合的噪声不舒适度增长率。故在预测噪声和振动的相对重要性时应该将二者之间的“掩蔽效应”考虑在内。

本实验的B部分（振动相对于参考噪声的不舒适度）中，振动不舒适度随客观幅值的增长率nv=0.706，同Morioka 和Griffin[21]的振动不舒适度平均增长率0.71 一致。在Morioka 和Griffin的实验里，受测者在评价2 s 振动不舒适度的过程中始终暴露在SEL为77 dB(A)的白噪声中；而在本实验的B部分，受测者在评价4 s振动不舒适度的过程中暴露在SEL为76 dB(A)的低频噪声中。在这两个实验中，受测者经历的噪声幅度相近，对振动激励的“掩蔽效应”也相近，因此得到的结果也相近。

3.3 等舒适度曲线的快速确定步骤

从表4可以看出，根据实验A部分（噪声相对于参考振动的不舒适度，见表2）的LAE和aVDV值得到的等舒适度曲线斜率，同根据实验B部分（振动相对于参考噪声的不舒适度）的0.58 m/s1.75和76 dB(A)得到等舒适度曲线斜率20nv/ns的值并不一致；甚至出现了错误值（符号*标注的值）。式（7）中斜率20.2是通过A部分和B部分幅度相近的噪声和振动值（即78.6 dB(A)和0.78 m/s1.75；76 dB(A)和0.58 m/s1.75）计算得到，同Huang 和Griffin 根据完整的交叉感觉实验提出的合理值21[12]相近。但是，不推荐使用这种方法得到斜率20(nv/ns)的值，因为仅使用两组测量数据（即实验A部分和B部分各一组SEL 和VDV）来进行线性回归可能产生较大误差，同时也无法确定数据的统计功效。

另一方面，将根据实验B部分得到的nv的值（0.706）除以根据实验A部分得到的ns/20的值（从0.019到0.036，中值为0.027），得出斜率20nv/ns值的范围为从19.6到37.2（中值为26.1）。这些值同之前根据实验得到的结果一致[12]。这说明如果获得nv和ns的实验是在相同的条件下进行，例如振动和噪声激励的特征（幅度、频率等）相同，受测者相同等等，20(nv/ns)的值可以直接通过nv和ns的比值计算。

以此可知，实际应用中可以通过如下步骤快速获得噪声和振动等不舒适度曲线：

（1）选取一个幅值的振动作为参考激励，评价不同幅值的噪声相对于该参考的不舒适度，通过线性回归获得ns；

（2）选取一个幅值的噪声作为参考激励，评价不同幅值的振动相对于该参考的不舒适度，通过线性回归获得获得nv；

（3）通过nv和ns的比值获得主观等效曲线斜率20(nv/ns)的值；

（4）通过斜率与一组噪声振动组合（如参考振动的VDV 和与参考振动不舒适度相同的噪声激励的SEL）计算出截距，这样就得到了噪声和振动的主观等效曲线。

4 结语

噪声和振动的等舒适度曲线描述了噪声和振动的相对重要性。本文通过主观评价实验，提出了两者等舒适度曲线的快速确定方法：当实验条件相同时，评价噪声相对于振动产生的不舒适度，或评价振动相对于噪声产生的不舒适度，噪声和振动的等舒适度曲线的斜率20nv/ns可以直接通过nv和ns的比值得到，从而较为快捷简便地得到噪声和振动的不舒适度等效曲线。

噪声和振动之间存在“掩蔽效应”：当受测者同时经历噪声和振动时，较大幅值的噪声会“掩蔽”较小幅值的振动，而较大幅值的振动会“掩蔽”较小幅值的噪声。