基于小波分析的混凝土箱梁桥应变监测数据的超载信息识别
2021-04-17张宪法孙晓燕顾永强
薛 刚,张宪法,孙晓燕,顾永强
(内蒙古科技大学 土木工程学院,内蒙古 包头014010)
近几十年来,健康监测技术在桥梁结构的使用、维护及加固改造方面起到十分重要的作用。小波技术在挖掘桥梁健康监测信息方面,有着独特的优势,可获得信号在不同尺度上的“信息增量”。赵华等[1]利用小波变换研究了数值仿真信号及实桥测试信号的车轴信息识别问题,结果表明,小波变换能提高桥梁动态称重系统的车轴信息识别精度。尤琼等[2]利用小波有限元对移动荷载识别问题进行了仿真研究,结果表明,与传统有限元模型相比,小波有限元模型以较少的单元在相同的识别时间内可获得相近的移动力识别精度。夏樟华等[3]建立了由健康监测系统测得的应变响应与移动荷载的线性回归方程,基于小波原理,提出了一种能有效应用于大跨度连续刚构桥的移动荷载识别方法。桥梁结构除了承受自重等恒载作用外,主要承受车辆的循环往复作用,当重载或超载车辆较为集中时,容易导致桥梁结构出现裂缝、桥面车辙甚至发生沉陷等破坏。按照国际公认的轴载换算方法,超限100%的货车作用一次对路面的破坏,相当于标准轴载作用16次产生的破坏[4],识别桥梁的车辆超重信息对在役桥梁的安全使用和及时维护都很有必要。
G210 线黄河公路大桥位于内蒙古自治区包头与鄂尔多斯市的交界处,为预应力混凝土箱梁桥,该桥是连接包头市白云鄂博与陕西等省通衢的重要组成部分。大桥全长831 m,上部结构采用一联11 孔预应力混凝土变截面连续箱梁,桥跨组合为(50 m+9×80 m+50 m)+2×5.5 m,该桥于2003年建成通车,在内蒙古经济建设中的地位举足轻重。为保障桥梁的安全使用,2010年起,桥梁运营管理部门在该桥安装健康监测与安全评估系统,采用实时监测、人工检测和定期测评相结合的方式,掌握桥梁结构的工作性能和病害损伤信息,实现对桥梁营运状态健康状况的实时监测和安全评估。本文根据小波原理,提取桥梁健康监测系统中的海量应变数据并进行预处理,对其中的异常信息进行分析及研判,从中识别出由超重车引起的应变响应信息,可丰富大跨度桥梁车辆超载的辨识手段及提高辨识效率,为制定桥梁安全运营的对策提供依据。
1 应变监测结果及分析
1.1 测点布置
G210 线黄河公路大桥健康监测系统共设置测点108个,其中应变测点60个,温度测点4个,支座截面和跨中截面静应变监测位置如图1所示。
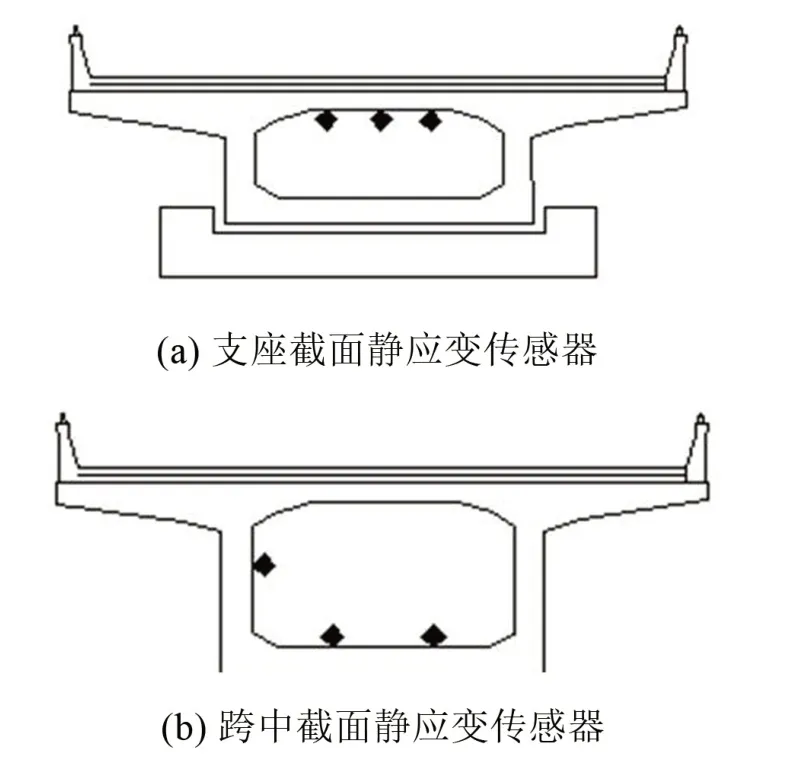
图1 健康监测系统中静应变监测位置
采用振弦式应变计监测G210 线黄河公路大桥的应变,其内置的温度传感器可同时监测环境温度,对应变予以温度补偿。为排除车辆及温度效应对桥梁结构初始应变的影响,于凌晨2:00 至4:00 间埋置振弦式应变计,该时段桥梁上的交通流量少,可最大程度降低车辆荷载对应变测量值的干扰,另外,该时段的应变埋置点没有阳光直射,箱梁内外温度相同,可最大程度降低温度效应对应变测量值的影响。
1.2 应变时程曲线特征分析
G210线黄河公路大桥纵向走位为南北向,选取由北向南第十跨跨中底板测点(后文简称为42#测点)应变作为研究对象。桥跨跨中底板的传感器对随机事件比较敏感,且受噪声影响较小。每15分钟采集一次数据,以天为单位,选取某一年的应变监测数据,将实时应变与本文2.1 节得到的初始应变作差,得到42#测点的应变时程曲线,如图2所示。
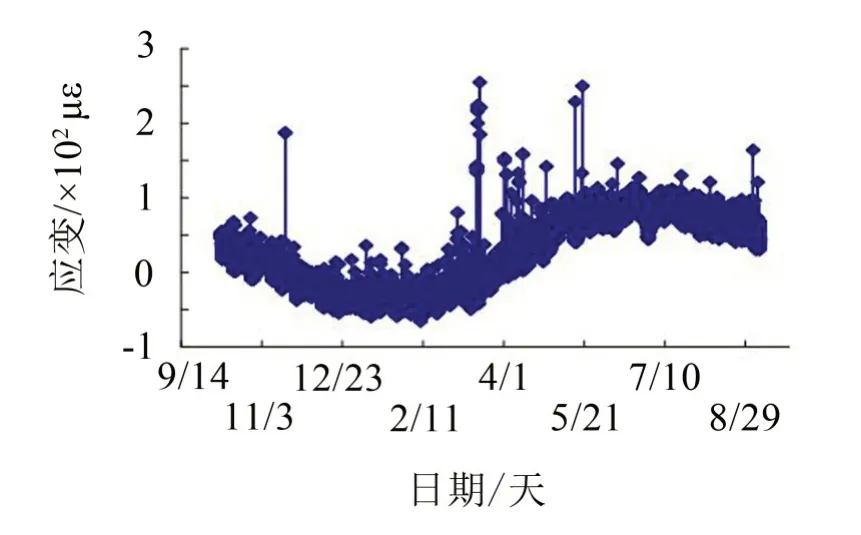
图242 #测点应变时程曲线
图2表明,42#测点的监测应变比较完整,可认为该位置的振弦式应变计的工作状态较为稳定。该测点应变的年度时程曲线呈正弦型,符合四季更迭规律,部分监测应变值有波动现象,呈现出振动强度大而出现次数少的特点。研究表明[5],大跨度桥梁应变监测数据的波动现象主要由超重车过桥、大风、突发强烈振动或地震动所引起,这些致因引发不同特征的振动。
常规载重车辆通过桥梁时,结构产生振动,应变时程曲线骤然增大后迅速减小,超重车辆通过桥梁时,产生的振动幅度为正常车辆产生振幅的数倍[6]。强风作用下桥梁结构的动态反应非常复杂,可引发风和结构物的相互作用,应变信号漂移且没有规律。地震动、人工爆破等突发的随机振动事件,引发的桥梁振动周期短且振幅大。
对G210 线黄河公路大桥的使用状况进行调查[7],在所考虑的时间段内,桥梁周围未突发剧烈振动及地震等偶然事件,也没有暴风作用,可以人为风荷载引起的效应远小于车辆荷载引起的效应。
1.3 应变监测数据的奇异值处理
传感器跳变产生的异常表现为监测数值较大且集中出现,该现象称之为奇异值簇集现象[8],如图3中某年度3月14日至16日的监测数据所示。通过分析各种异常事件的特点可对监测数据进行数据预处理。
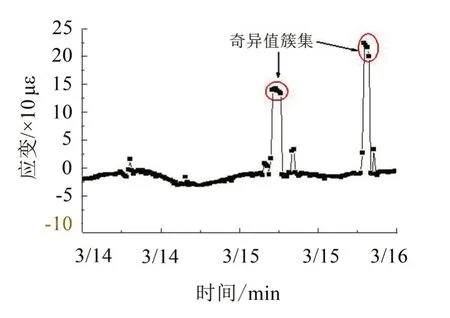
图3 监测数据的奇异值簇集
图2中部分数据变化剧烈或出现奇异值簇集现象,并非由车辆荷载引起,称为奇异值异常。通常情况下,某采样点与其相邻采样点差值绝对值大于200 με,或该采样点出现奇异值簇集现象,该采样点信号被视为奇异值异常。根据监测信号识别超重车辆信息,进而预测全年的超重车辆信息为概率问题。在所考虑的时间段内,桥梁周围无剧烈振动、地震、暴风等事件,所以,对奇异值异常数据做剔除处理,预处理后的应变监测值异常考虑为由车辆荷载所产生。
采用MATLAB软件对42#测点的监测数据进行编程预处理,预处理后的应变时程曲线见图4。
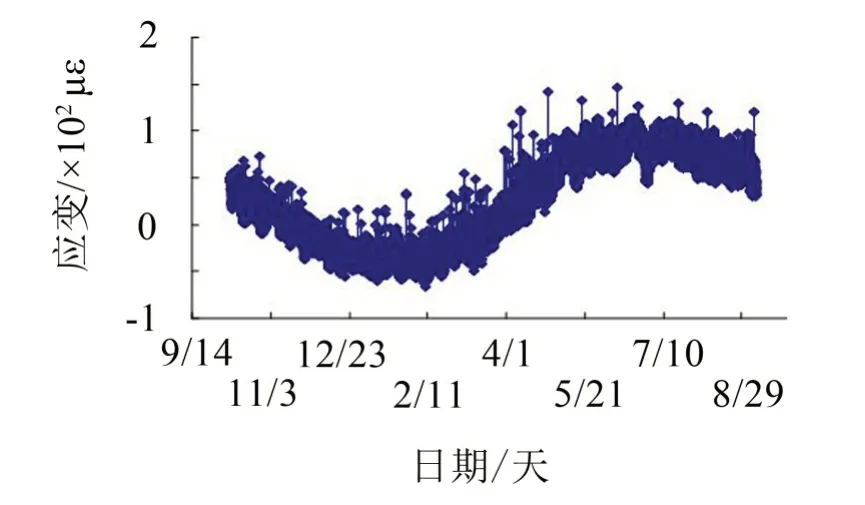
图4 42#测点预处理后的应变时程曲线
一般而言,营运阶段的大跨连续箱梁的应变主要由自重荷载、温度荷载、车辆荷载及风荷载综合作用产生的,就荷载特点而言,自重荷载、温度荷载的变化较为缓慢,而车辆荷载和风荷载作用时间短,且无规律可循,随机特征更加明显。桥梁结构某点的总应变可表示为
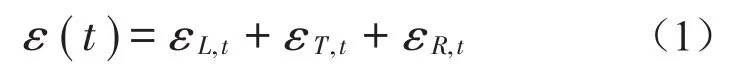
式中:εT,t+εR,t,εC为混凝土的长期收缩和徐变应变,混凝土的收缩和徐变在施工及成桥前期比较明显,大约经过5年~10年混凝土的收缩徐变达到一个极值,黄河大桥2003年建成通车,本次桥梁健康监测距离建桥通车已接近10年,混凝土收缩徐变已基本完成。εM为结构自重荷载,该值在桥梁结构总应变值ε(t)中的比重最大。
εT,t为热应变,是由温度效应而引起的应变,在桥梁受力过程分析中非常复杂,本次桥梁结构监测应变数据每15分钟采集一次,15分钟内的温度效应变化微小,不至引起应变监测值ε(t)的突变。
引起应变值εR,t的随机荷载主要包括车辆荷载、风荷载等。研究发现[9-10],风荷载对桥梁结构的作用非常复杂,考虑本桥桥址的环境和桥型,风荷载产生的桥梁结构受力与车辆荷载相比相对较小。汽车过桥时,汽车荷载会使得应变监测数据组成部分εR,t产生激烈变化,该值相对于相邻采样点表现出反常的特征,车辆荷载越大异常现象越显著,该特点可用于在应变监测数据中识别出超重车辆。
2 小波技术在信号异常诊断中的应用
2.1 小波检测信号的基本原理
由式(1)可知,总应变ε(t)是由3种不同的应变组成,3种应变具有不同的时间尺度,小波分析对于分解不同频率、尺度的数据具有明显优势[11]。利用小波变换对信号进行多尺度分析,在信号出现突变时,小波变换后的系数具有模量极大值,通过检测模量极大值点可确定异常事件发生的时间点。
对应变数据进行离散小波分解[12],如式(2)所示:
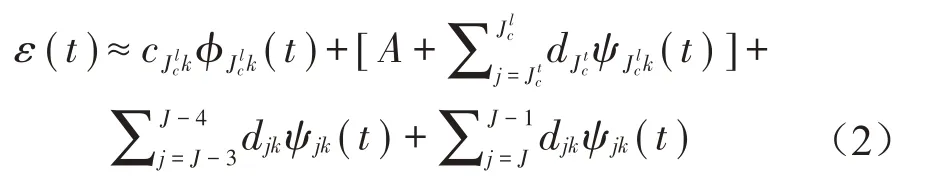
式中:cJclk为持续荷载作用下收缩徐变的尺度系数,dJct为温度引起的应变变化的小波系数。小波分解系数djk与ε(t)的组成部分(式(1)中的εR,t)变化同步。
正常情况下应变ε(t)随时间变化光滑,突变将导致ε(t)变化不连续,相应的djk比邻近的点要大的多。小波系数djk代表数据的波动程度,而波动程度的大小判定则可以通过与一个关键阈值进行比较实现,超过该关键阈值即被认为应变类数据产生突变,通过记录那些已识别的比阈值大的小波系数的位置,可将潜在的异常信号可从应变时间系列中提取出来。关键阈值按式(3)计算[13]:
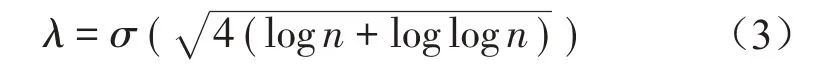
式中:σ是反映监测数据噪声水平的参数,按式(4)计算[14]:
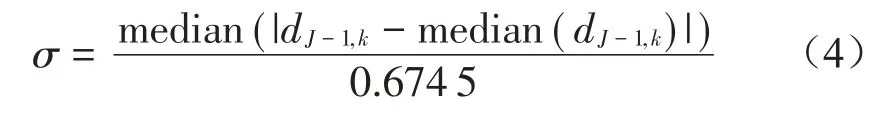
式中:J=log2(n),n为信号的长度,median(dJ-1,k)为数据序列dJ-1,k的中位数。
2.2 信号超重信息的小波诊断结果
选取第十跨跨中底板箱梁内侧底板应变数据进行分析。对预处理后的实测数据进行小波分解并获得相应小波系数,并将小波系数与关键阈值进行比较,识别超重车,具体技术路线见图5。
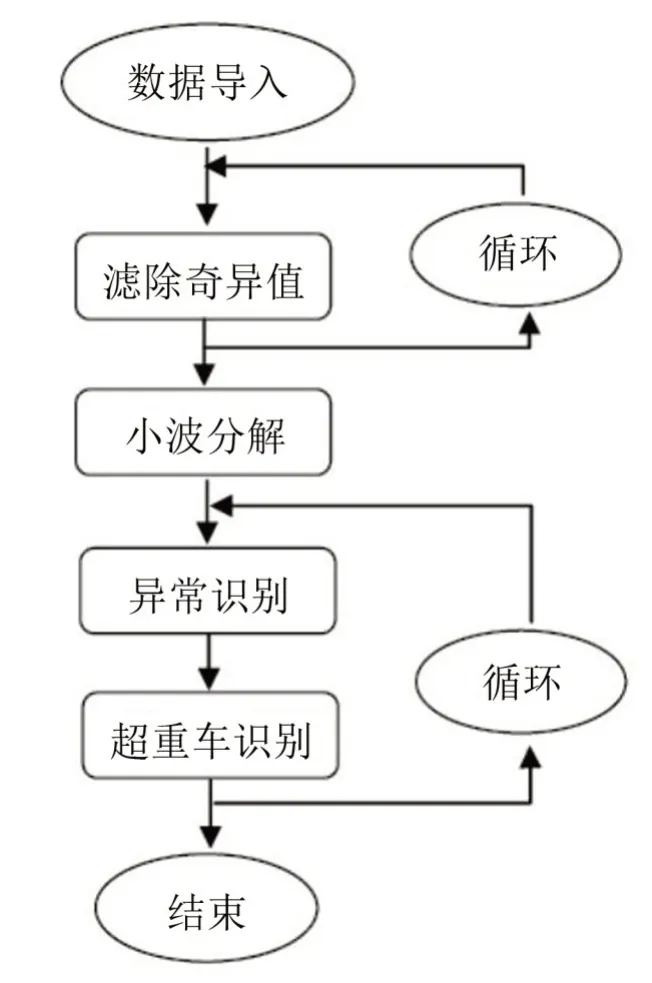
图5 超重车辆小波识别技术路线
以第42#测点某个月的数据为例进行详细说明,该时间段实测应变值经预处理后,如图6所示。
利用MATLAB的Db(4)小波程序,将42#测点经预处理后某月份的实测应变监测数据进行两层分解,得到细节系数,图7中较深颜色线代表监测信号,较浅颜色线表示小波分解第2层细节信号。
提取分解出的第2层细节信号,并根据式(3)计算得到关键阈值λ为4.28,将小波细节系数与关键阈值进行比较,记录超过关键阈值的细节系数所对应的应变信号并记录其位置。图8展示了300个应变监测信号的细节系数及识别出的奇异值点。
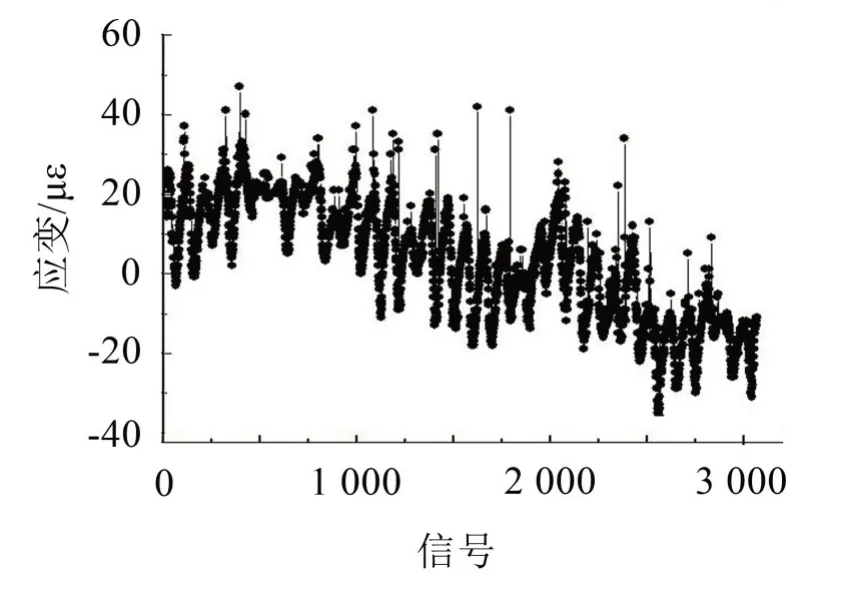
图6 42#测点经预处理后的某月份的应变监测数据
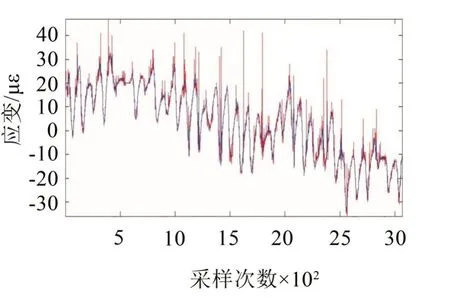
图7 42#测点某月份应变信号及其小波细节系数
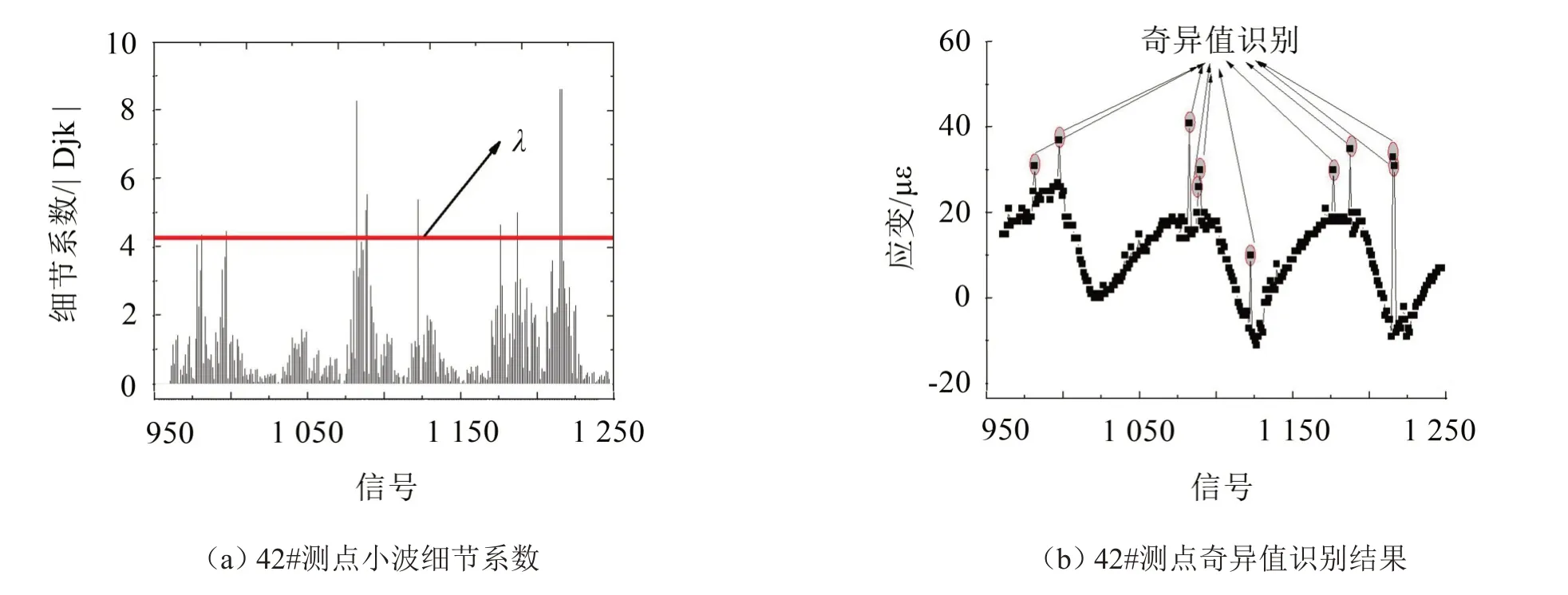
图8 42#测点某时间段应变小波细节系数及奇异值识别结果
图8中识别出的异常点跳跃方向一致,反映了识别数据的可靠性。对从42#测点所提取时间段的监测数据进行统计并识别,得到467个奇异值。
车辆荷载作为动荷载加载在桥梁结构是瞬时加载,正常车辆经过桥面时,桥梁结构会产生应变值的改变,表现为由弱变强再转弱,重型车辆过桥时引起的桥梁振动幅度通常是正常通车的数倍,即重型车辆通过桥面时跨中底板的应变值比车辆正常通行时引起的应变值大,这就为识别超重车辆提供依据。
2.3 应变阈值界定
预应力混凝土桥梁结构营运阶段受力比较复杂,不考虑温度效应时,桥梁结构主要承受预应力、自重荷载及车辆荷载的作用。为获得车辆荷载作用下桥梁结构产生的应变,建立有限元模型,并施加预应力、自重及车辆荷载,将有限元计算结果减去同时施加预应力及自重作用时产生的应变,两者差值即为车辆荷载产生的应变,42#测点在车辆荷载作用前的压应变值为-502.83 με,将其作为初始值。依据该桥设计时使用的《公路桥涵设计通用规范》(JT J021-1989),并参考现行规范,考虑3种运营工况:工况1为一辆QC-20重车(55吨)加载;工况2为两辆QC-20 主车(30吨)并排加载;工况3为符合实际车流状况的车队加载,模拟车辆正常行驶过程。3种工况车辆轴距、轮距及载重参见文献[7]。3种工况下桥梁第十跨跨中底板应变响应如图9所示。
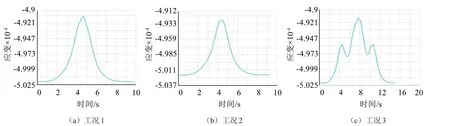
图9 3种工况下第十跨跨中底板应变响应
将3种车辆运行工况下的有限元计算结果减去应变初始值,可得到3种工况下车载在该测点的静应变分别为11.02 με、10.70 με 和9.27 με。考虑该桥车辆的冲击系数为0.116[15],取工况1 测点的静应变11.02 με 算得该测点处车辆作用的应变幅阈值,为11.02×(1+0.116)=12.29 με,超过该阈值的应变为超重车辆产生。
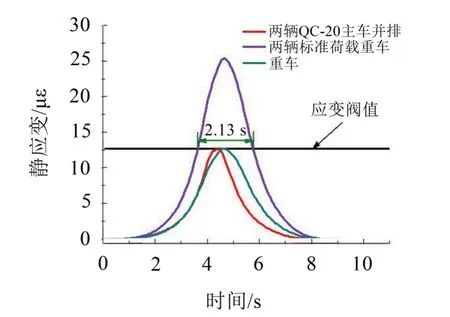
图10 不同加载情形跨中底板应变响应
车辆行驶速度为12 m/s,整个桥长831 m,走完全桥不超过68 s,而传感器的采样周期为15分钟一次,正常载重的汽车经过时被监测系统捕捉到的概率非常小,汽车越重捕捉到的概率越大。图10为不同载重情况下测点的应变响应,由此可知,一辆两倍标准荷载的超重车产生的应变值超过阈值的时间间隔是2.13 s,按照15分钟的采样间隔时间计算,超重车被捕获的概率为2.13÷(15×60)=0.237 %。
2.4 超重车辆识别及数量估计
样条插值具有收敛快的优势,同时可在非线性插值中增加节点来改进光滑度。本文采用三次样条插值原理,利用MATLAB软件编程计算出该奇异值时间点的“理论值”,将奇异值与“理论值”做差后与应变幅阈值比较,若超过该应变幅阈值,则认为这是由于超重车辆作用而产生的。
基于MATLAB识别出该时间段共存在146个应变幅超过应变阈值,超出阈值的应变幅的概率密度柱状图为图11,该概率分布符合一般活荷载的极值I型分布,可用式(5)进行函数拟合:
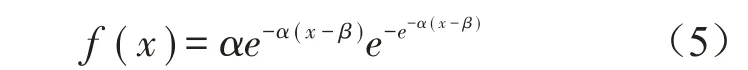
式中:α表示尺度参数,β表示位置参数。拟合结果为图11中的红颜色线,该拟合曲线较好地反映超出阈值的应变幅的概率分布,拟合效果较好。此时,α为0.234 45,β为25.635 8。
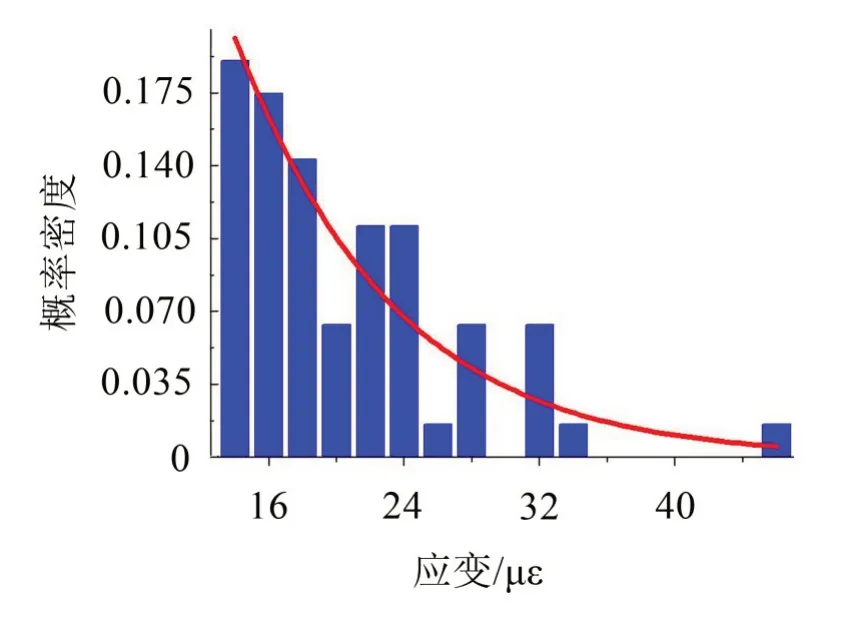
图11 超出阈值的应变幅概率及拟合曲线
图11所示的拟合曲线较好地反映了超出阈值的应变幅的概率分布规律,说明超重信息的识别结果是可靠的。根据本文图10可知,超重车信息被捕获的概率为0.237%,按照本文选取的330天的应变时程,可概率估算出该桥在本文所取年份内经过的超重车为67 510辆,日均超重车约187辆,与在G210线黄河大桥收费站同期历史记录基本相符。
3 结语
本文提取G210 线黄河大桥健康监测系统中的海量应变数据,对第十跨跨中底板42#测点的数据进行分析,利用小波原理识别出超重信息,得出以下结论:
(1)自重、收缩徐变效应以及温度效应产生的应变在监测过程中变化缓慢,不会产生应变信号的突变,预处理后的监测数据的奇异值由车辆过桥引起。
(2)利用小波原理对桥梁的应变监测数据进行两层小波分解,确定其关键阈值,将小波细节系数与关键阈值进行比较,可对超出关键阈值的应变信号进行奇异值识别,识别效果较好。
(3)依据现行规范设置不同荷载工况,得到重车驶过42#测点时的应变幅阈值为12.29 με。根据有限元分析得到超重车产生的应变值超过阈值的时间间隔是2.13 s,按照本文选取的监测时间段,从概率上估算出该年份日均超重车辆为187辆,与黄河大桥监测站同期的历史记录基本相符。
