基于K-means和SOM的水下传感器数据采集方法

洪 悦，郭承军

（1.电子科技大学电子科学技术研究院，成都611731；2.电子科技大学通信抗干扰技术国家级重点实验室，成都611731）

引 言

随着海洋资源勘探和污染物监测工作的开展，各种关于海洋水文数据的采集技术不断发展成熟。其中水下无线传感器网络（Underwater sensor networks，UWSNs）就是对海洋信息采集的重要技术之一。水下无线传感器网络可以根据具体应用不同，分为多种系统结构。例如，根据监测的空间区域不同大致可分为二维、三维和海洋立体监测网络3种。本文研究的是应用于深海环境的二维监测网络结构。在该模型中，传感器节点被锚定在海底，采集到的信息通过水下机器人（Autonomous underwater vehicle，AUV）定时收集，最终将采集到的海底信息实时地传送给地面系统［1-3］。

传感器节点数据传输方式有多种，水生通讯就是其一。相比于水下电磁波在水中的衰减比较严重，不适合非接触式信号传输而言，水声非接触式信号传输是一个很好的选择。中科院沈阳自动化研究所研制的“探索者”号无缆自治水下机器人的信息系统，实现水声通讯完成水上水下信息交换［4］。由于在近海及海面有噪声干扰，所以水声通讯更适合于深海环境。东北大学（美）Woods Hole海洋科学研究所在深海条件下，实现185.2 km（100海里）的水声通讯，数据传输速率达到1 Kb/s［5］。美国海军组建的实验性远程声纳和海洋网络计划的水声网络，通过海面的浮标将水下信息中转至陆空各种平台。由于在深海条件下，铺设电缆是比较大的工程，而非接触式通讯的通讯距离有限。在AUV技术不断成熟的条件下，使用AUV对深海条件下声传播传感器实现定时数据收集是一个比较好的选择，而在使用AUV对传感器节点进行数据采集的方法中，不得不考虑路径规划问题。2014年，Basagni等提出了一种贪婪的自适应AUV路径规划算法［6］，该算法实现了传输数据的信息量最大化。2012年，Hollinger等［7］提出了用改进的TSP算法遍历最大独立集的方法收集数据。伊君［8］提出了基于K-means的水下传感器网络AUV数据收集方法，通过K-means划分多个网络子集的方法产生最优路径。本文是在针对水下传感器节点稀疏情况下，AUV既可以遍历节点又可以根据传感器传播特点尽可能地优化路径。传感器节点在实现各种网络协议和应用系统时，存在以下一些现实约束［9］：传感器节点体积限制着电池能量；无线通信的能量消耗与通信距离的关系为E=Kdn，即距离d的增加会增加传感器节点的能耗，基于此，一般传感器节点的通信半径设置在100 m以内；最后，高存储能力和高处理能力意味着高价格。

由于通信半径的限制，本文将通信半径ρ设置为100 m。采集点设置为通信半径ρ覆盖区域内距离节点90 m的点位；AUV到达数据采集点进行数据采集。

AUV采集数据也是旅行商（Travelling salesman problem，TSP）问题。自组织映射网络（Self-organizing map，SOM）方法是解决TSP问题的方法之一。和传统的聚类方法相比，SOM网络能够映射到一个曲面或平面上，从而保持拓扑结构不变。SOM与Hopfield神经网络［10］算法比较，优势在于其避免了陷入局部最小值现象，具有更快的速度和更高的精度。

本文最主要的是解决传感器节点的数据采集点的确定问题，只有确定采集点位置，才能用TSP进行路径规划。采集点的确立一方面是因为AUV无法真正到达传感器节点，另一方面确立合适的采集点可以缩短路径长度，提高效率。本文采用K-means算法协助确立合适的采集点。

1 SOM解决路径规划算法

SOM路径规划算法的主要原理是每次找到离节点最近的神经元，该神经元被称为优胜神经元，然后以该神经元建立一个高斯分布逐渐更新其他神经元的位置，也就是更新输出神经元权值向量，通过不断的迭代，输出神经元会逐渐学习到输入数据背后的模式。在TSP问题中二维传感器坐标或者采集点坐标就是输入数据，传感器或者采集点空间位置就是网络需要学习的模式，在迭代的过程中，为了保证算法的收敛，会更新学习率等参数，最终达到神经元不断地靠近节点的目的，最终输出一条最短遍历节点回路［11-13］。

当将SOM应用于TSP时，输入层中的每个节点都表示一个传感器节点或者采集点节点，并用笛卡尔坐标（Cx，Cy）表示其位置。输出层神经元的权值与输出层神经元在同一个维度，表示神经元的位置。由于TSP的基本要求是访问所有节点并最终返回起点，因此输出层使用了一个圆形拓扑。在形成这样的拓扑结构之后，神经元在整个训练过程中竞争成为赢家，这一过程采用了由两个不同的过程组成的无监督策略。输入的第q个节点的向量表示形式为

与第j个输出节点相关联的权重的向量表示形式为

SOM算法如下：

（1）初始化输出层各个节点的权值wji∈（0，1），i=x，y，j=1，2，…，n。同时指定学习速率α(t)的值和邻域函数f(d，G)，t为迭代次数，T为总学习次数。邻域函数表示在步骤（5）中确定的获胜神经元的邻域。

（2）随机选取一个样本数据提供给输入层，并进行标准化处理。标准化处理目的在于方便步骤（4）中计算欧氏距离以确定获胜神经元。

（3）对输出层的权重进行标准化处理。这里同样是为了计算欧氏距离。

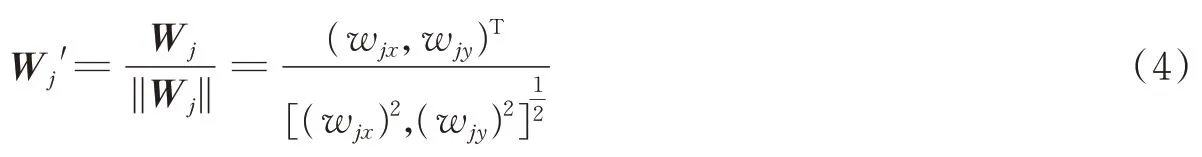
（4）计算输入样本点Cq′和所有输出层节点Wj′之间的欧氏距离。

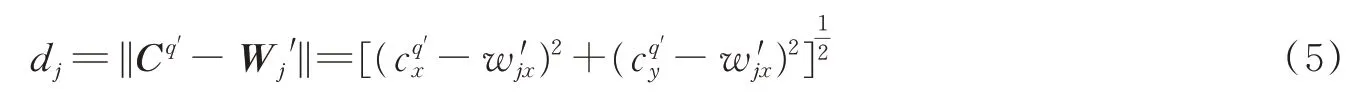
（5）从步骤（4）计算得到的欧氏距离中，找出最小的距离dc，即为获胜神经元。

（6）为了向目标节点靠近，对获胜神经元及其邻域内神经元的权值进行重新计算，而不在邻域内的神经元，则保持不变。

（7）不断重复步骤（4～6）直到到达目标迭代次数或者学习率到达阈值为止。

在SOM学习过程中，学习速率α(t)决定学习时间，若学习速率α(t)设定过大，这里指接近1，则会导致权重的更新幅度过大而产生振荡，这会造成学习的不稳定性。相反若把学习速率α(t)设定过小，这里指趋于0，则会造成权重更新幅度过小，从而使收敛时间过长。在学习过程中动态地调整学习率可以解决这一问题。学习速率公式为

式中：α0为初始设定的学习率；α(t)为t时刻的学习率，α(t)∈(0，1)；t为迭代次数；T为指定的迭代总次数。此外，邻域函数f(d，G)也可以同学习率一样设置为动态的可调整状态。动态设定邻域值，不仅可以加速学习过程，又可以保证学习的必然收敛，并且可以降低造成网络扭曲的可能性［14-19］。可以用多种形式设定该函数。本文设置邻域函数为

式中：G为时间的单调递减函数，d为邻域神经元和获胜神经元的坐标距离。

本文采用的是已经公布的TSP数据集，首先以1 200 m×1 750 m内52个传感器的节点进行实验，经过SOM的路径规划可以得到优化的路径规划图。通过SOM规划的路径长度为l1=7 874.59 m（最优值为l0=7 542 m），如图1所示。

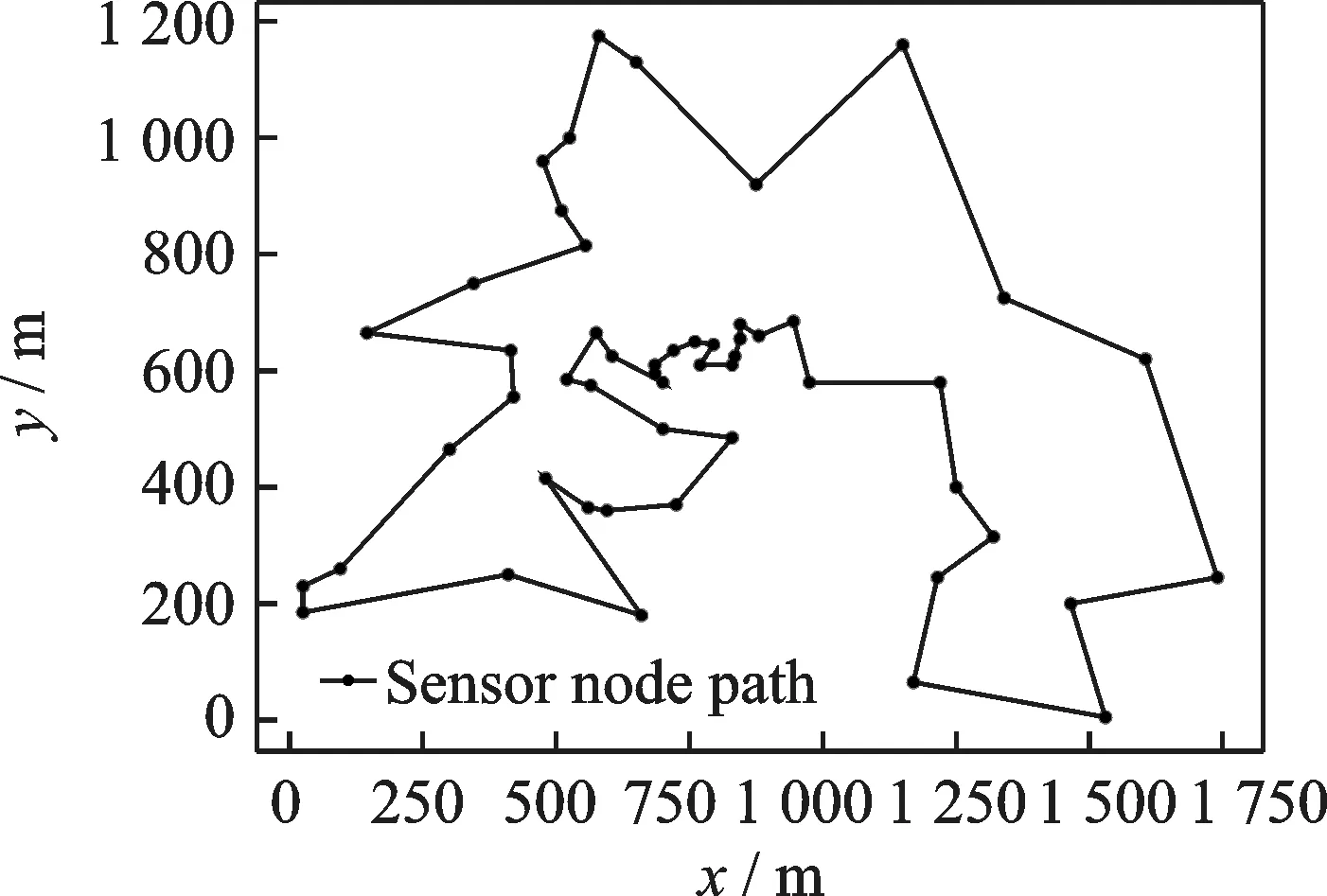
图1 传感器节点SOM路径规划图Fig.1 SOM path planning diagram of sensor node

2 K-means算法得到采集点位置

K-means算法是一种通过迭代求解的聚类分析算法［20-21］。K-means算法中的K代表类簇个数，Means代表类簇内数据对象的均值。K-means算法以欧式距离作为数据对象间相似性度量的标准，即数据对象间的距离越小，则它们的相似性越高，它们越有可能在同一个类簇。

K-means算法具体实现步骤为：先根据数据的先验知识选择一个合适的K值，然后选择K个初始的质心。由于K-means算法是启发式算法，K个初始化的质心位置选择对最后的聚类结果和运行时间都有很大影响。本文根据之前基于SOM算法对传感器节点路径规划图形的分析，拟采用4个聚类中心，即K=4。K-means算法首先对数据进行预处理，将数据按比例放置在1×1的二维坐标内

因此可将4个初始类簇中心设置为（0.75，0.75），（0.25，0.75），（0.25，0.25），（0.75，0.25）；接着根据欧式距离划分所属类簇中心，欧式距离计算公式为

然后根据所属类簇中心K的点对类簇中心的坐标进行重新计算

式中：Mk为第k个类簇中心，|Mk|为第k个类簇中心的数据个数。接着再重新划分所属类簇中心的点，并重新计算类簇中心的坐标，不断迭代，直到所属类簇中心的点不再变化为止；最后再将类簇中心和所有的点按比例还原到原来的坐标，如图2所示。

五角星表示4个类簇质心，其他包括点、三角形、正方形和叉等形状的坐标分别代表所属4个类簇中心的传感器点，且每个类簇中心都被所属传感器节点包围。将形成的4个类簇中心放进传感器节点规划的路径中，如图3所示。

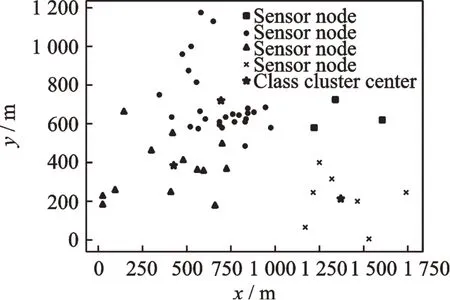
图2 K-means算法传感器节点类簇中心Fig.2 K-means algorithm sensor node class cluster center

图3 K-means算法聚类中心在规划路径中Fig.3 K-means algorithm clustering center in the planning path

从图3可以看出4个聚类中心都在规划路径的内部，右上侧的类簇中心较靠近路径边界，从图2可以分析出该类簇中心的点位只有4个，数量较少且坐标差异较大，因此不能将类簇中心理想地放置在规划路径的内部较中心的位置，但对结果影响不大。

K-means算法原理比较简单，实现也很容易，收敛速度快。虽然算法的最初需要根据经验设置K值和初始类簇中心，但是聚类效果较优，符合本文的要求。

3 算法流程

根据前文的介绍，首先根据传感器节点通过SOM对路径进行规划；然后根据规划出的路径进行图形分析，确定K-means算法初始类簇中心和K值，通过K-means算法计算出最终的类簇中心；其次根据式（16）确定采集点位置。

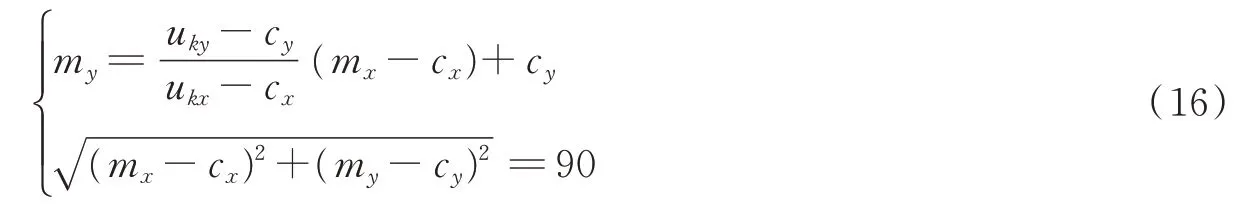
式中：Uk（ukx，uky）为第k个类簇中心，C(cx，cy)为属于第k个类簇中心的传感器节点，M(mx，my)为采集点。最后，对采集点进行路径规划，分为两次，第一次是引用传感器节点路径规划连接方式得到路径，第二次对采集点重新进行SOM路径规划得到路径。具体算法流程如下：

（1）输入n个二维传感器节点(C1，C2，…，Cn)，第q个节点坐标表示为。

（2）使用SOM对输入传感器节点进行路径规划，且得到路径连接序列，α0=0.8，神经元个数为8n。

（3）将传感器节点按比例缩放至1×1的坐标系内，对图形进行分析，确定初始类簇中心U0以及K的值。

（4）使用K-means算法进行类簇中心计算，重新得到Uk（ukx，uky），k=1，2，…，K。

（5）将传感器节点和类簇中心代入式（16）计算得到n个采集点(M1，M2，…，Mn)，将采集点坐标还原。

（6）对采集点按照步骤（1，2）得到的序列连接，得到路径规划图。

（7）对采集点按照步骤（1，2）SOM重新进行路径规划。

4 实验分析

本文的实验数据采用的是TSP数据，模拟1 200 m×1 750 m范围内52个传感器节点的环境。如图4所示是采集点根据传感器节点路径规划的路径图。从图4可以看出节点连接方式不变，总路径长度为l2=7 347.49 m，图形形状也大致不变，但是左下方区域有突兀，可重新进行路径规划。

图5将传感器节点路径规划线路和采集点路径规划线路放在一张图上进行对比。图5中虚线部分为传感器节点路径规划线路，实线部分是采集点路径规划线路，可以看出采集点路径规划图基本是在传感器节点路径规划连线的内部。

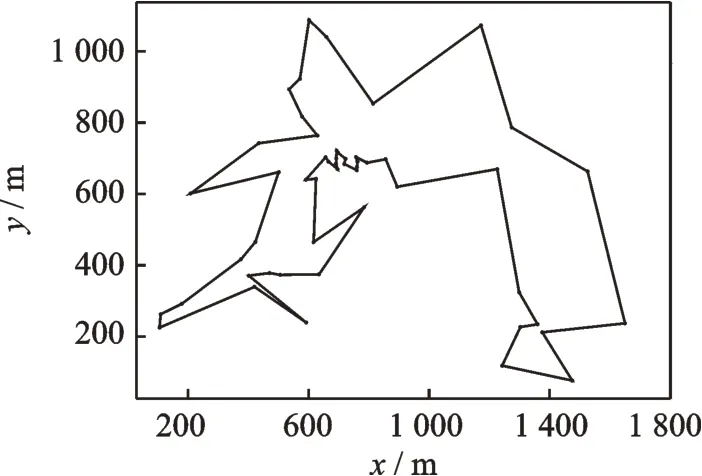
图4 采集点路径规划图Fig.4 Path planning diagram of collection point

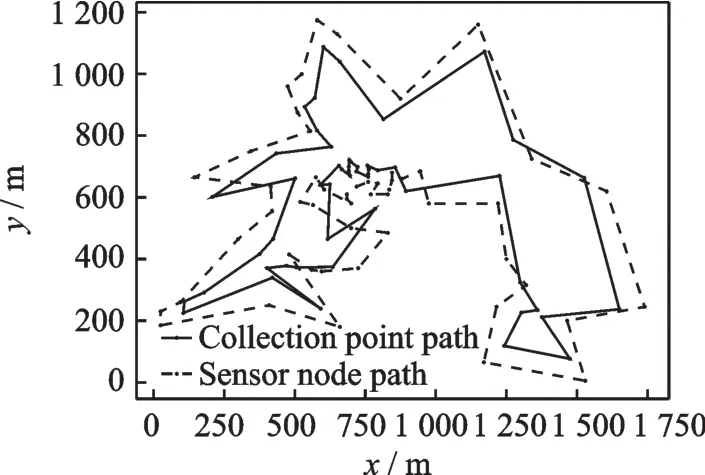
图5 采集点和传感器节点路径规划图Fig.5 Path planning diagram of collection point and sensor node

图6是重新进行路径规划后的图，l3=6 721.65 m。表1为路径长度对比结果。通过表1数据分析，传感器节点路径规划长度l1=7 874.59 m，采集点以相同的连接方式规划的路径长度为l2=7 347.49 m，优化了6.7%。根据TSP数据提供的最优解，传感器节点最优解l0=7 542 m，对采集点重新规划后优化解l3=6 721.65 m，优化了12.2%。可以看出，通过本文的算法在得到采集点的同时可以优化路径。

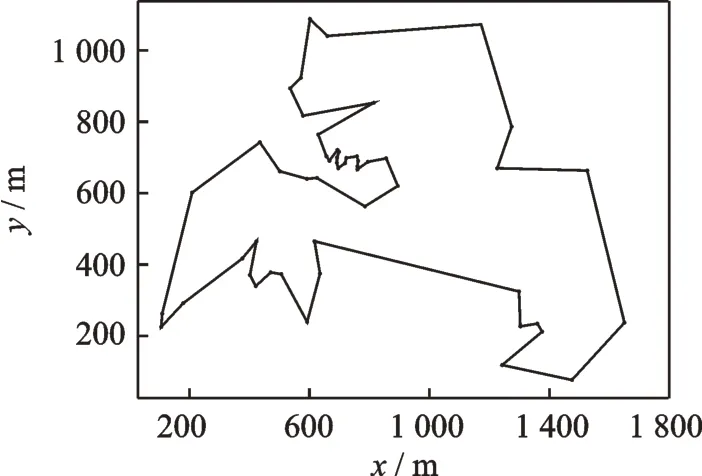
图6 采集点重新路径规划图Fig.6 Repath planning diagram of collection point

表1 路径长度对比结果Table 1 Comparison results of path length

本次实验增加了在多个不同传感器节点数量的情况下，验证该方法的实验效果。具体情况分别如图7～9所示。图7表示在2 500 m×4 000 m的范围内48个传感器节点的路径规划结果，图8表示在2 000 m×4 000 m的范围内100个传感器节点的路径规划结果，图9表示在2 000 m×4 000 m的范围内150个传感器节点的路径规划结果。根据仿真得到的具体数据如表2所示。

图7 48个采集点和传感器节点路径规划图Fig.7 Path planning diagram of 48 collection points and sensor nodes

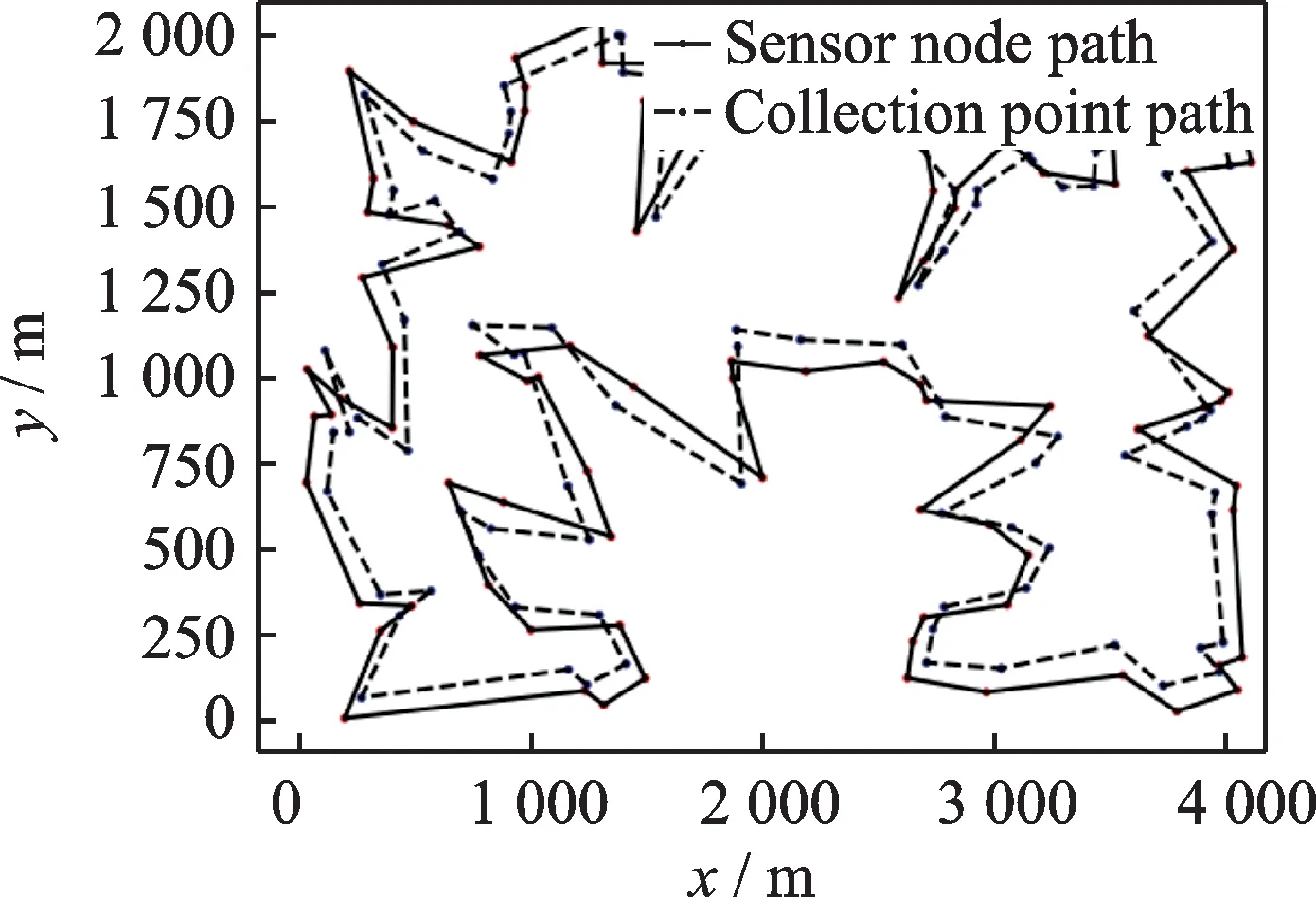
图8 100个采集点和传感器节点路径规划图Fig.8 Path planning diagram of 100 collection points and sensor nodes

图9 150个采集点和传感器节点路径规划图Fig.9 Path planning diagram of 150 collection points and sensor nodes

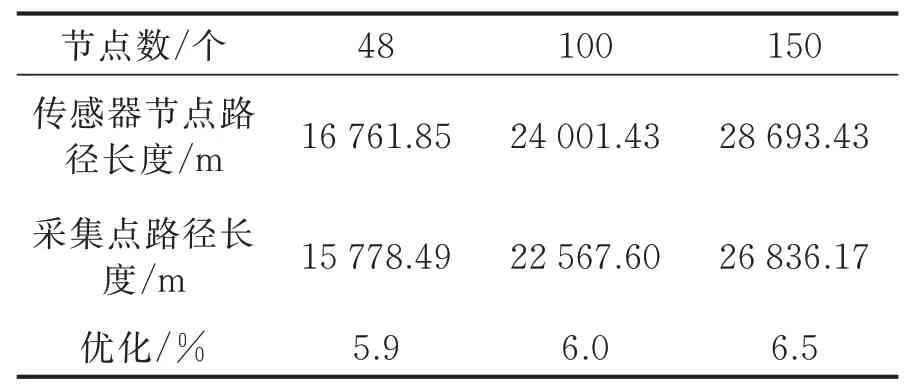
表2 不同节点的实验结果Table 2 Experimental results of different nodes

从表2数据可以看出，随着传感器节点的增加，此种方法能达到预期的效果，即不管是48个传感器节点，还是增加到100个传感器节点及以上，路径规划可以优化6%左右。

5 结束语

本文利用K-means算法和SOM路径规划算法对AUV采集水下传感器数据的路径进行规划。算法需要对传感器路径规划图进行初步分析，进而得到初始类簇中心，如果在传感器节点较庞大，所形成图形较复杂情况下，会增加难度。本文考虑的是距离传感器节点长度90 m的情况，实际可以根据传感器参数以及电源能耗更改。总的来说，本文适用于AUV遍历稀疏布置的水下传感器节点收集数据。在深海条件下，由于地质结构没有那么复杂，所以可以用二维平面的模型来进行路径规划，若是在地质结构更为复杂的新浅水区或者陆地，需要进行三维规划。同时，在有障碍物的情况下，也需要加入避障处理。在传感器节点稀疏的情况下，遍历每个节点是一个方便的选择，若在密集情况下，增加网络子集也不失为一个好的选择。