线性权互补问题的新全牛顿步可行内点算法

迟晓妮,张睿婕,刘三阳

(1.桂林电子科技大学数学与计算科学学院,广西 桂林541004;2.桂林电子科技大学广西密码学与信息安全重点实验室,广西 桂林541004;3.桂林电子科技大学广西自动检测技术与仪器重点实验室,广西 桂林541004;4.西安电子科技大学数学与统计学院,陕西 西安710071)

1.引言

作为互补问题[1]的推广,权互补问题[2]在科学和工程等领域有着广泛的应用.Potra[2]证明了Fisher市场均衡问题可以建模为非线性互补问题[3],也可以建模为权互补问题,但后者在某些情况下能得到更高效的数值解方法[4].全牛顿步内点算法[5]是求解线性规划的热门算法.2003年,Darvay[6]基于连续可微函数提出求解线性规划的新全内点算法,并给出了该算法的迭代复杂度.随后,Darvay[7]等人又提出求解线性规划的新全牛顿步内点算法,并分析了算法的多项式迭代复杂度.由于权向量非零,权互补问题的理论[8]和算法研究相比于互补问题更为复杂,因此关于权互补问题的算法尚不多见.Potra[9]设计了一种预估-校正内点算法[10]用于求解充分权互补问题.

本文将文[11]中P∗(κ)线性互补问题全牛顿步可行内点算法的连续可微函数推广到权互补问题,对中心路径进行等价变换得到新搜索方向,给出求解Rn上线性权互补问题的可行内点算法.该算法采用全牛顿步,避免进行线搜索求解步长,节省了计算时间和内存.分析了算法的可行性,并证明其迭代复杂度与目前线性优化最好的多项式时间复杂度相同.数值算例结果表明算法的有效性.

2.算法

考虑Rn上的线性权互补问题(LWCP)[1]：寻找向量对(x,y,s)∈Rn×Rm×Rn使得

其中A ∈Rm×n,b ∈Rm,c ∈Rn,ω ∈Rn++.定义LWCP(2.1)的严格可行域为}

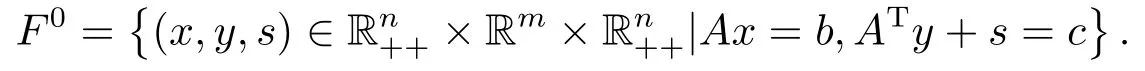
令初始点(x0,y0,s0)∈F0,ω(t)=tx0s0+(1−t)ω,其中t ∈[0,1] 且t0=1.考虑(2.1)的扰动问题

这里e=(1,··· ,1)T.假定A为行满秩矩阵,即R(A)=m.若内点条件(IPC)[5]成立,即(x,y,s)∈F0,则对任意参数t ∈(0,t0],方程组(2,2)有唯一解(x(t),y(t),s(t)).集合{(x(t),y(t),s(t))|t>0}称为LWCP(2.1)的中心路径.当t →0时ω(t)→ω,得LWCP(2.1)的最优解.

考虑线性优化问题内点算法中的连续可微函数[6]φ:R+→R+,并假设其反函数φ−1存在.用等价变换替换LWCP的扰动问题(2.2)中第三式,则新牛顿搜索方向(∆x,∆y,∆s)应满足方程组

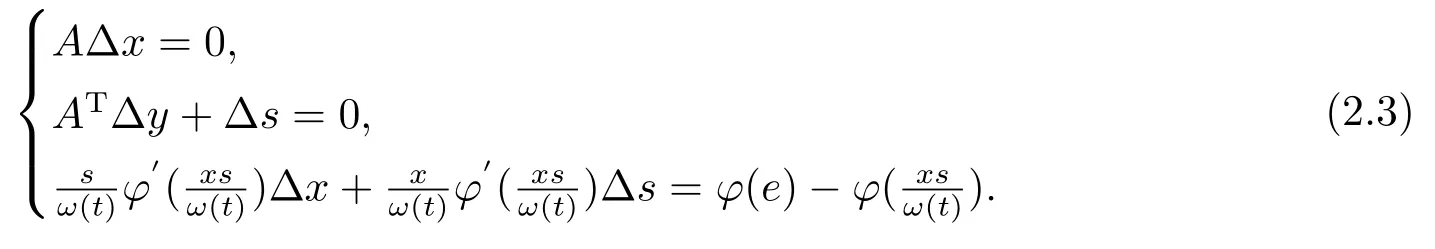
定义

由(2.4)式可知,方程组(2.3)可化为

其中:=AV −1X,V:=diag(υ),X:=diag(x),W(t)=diag(ω(t)).

将P∗(κ)线性互补问题的全牛顿步可行内点算法中的函数[11]推广到LWCP(2.1),则方程组(2.5)可化为

定义邻近测度

令

引理2.1[5]若u与v正交,则

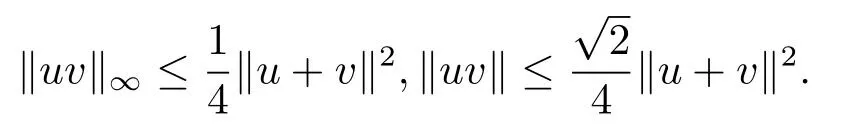
由方程组(2.6)知dTx ds=0.因此由(2.8)式得

由引理2.1和(2.7)式可知

引理2.2对任意υ ∈Rn,有

选取适当参数θ及任意初始点x0>0,s0>0,y0= 0,令ω(t0)=x0s0,其中t0= 1.显然δ(x0,s0,ω(t0))=0.求解方程组(2.6)并结合(2.4)式得牛顿搜索方向(∆x,∆s,∆y),其中t+=(1−θ)t,θ ∈(0,1).令新迭代点

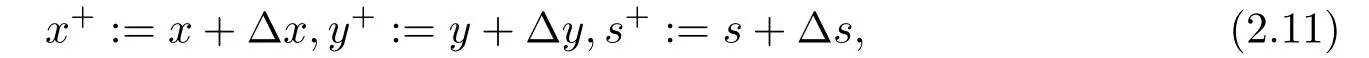
满足内点条件并且δ(x+,s+;ω(t+))<βt+.当∥xs −ω∥≤ε时,算法终止.下面给出本文算法的具体步骤.

算法2.1求解LWCP的新全牛顿步可行内点算法

步1 选择参数t0= 1,ε >0,β ∈(0,1),初始点(x0,y0,s0)∈F0,y0= 0且ω(t0)=x0s0.置k:=0.

步2 当∥xs −ω∥≤ε,算法终止;否则转步3.

步3 求解方程组(2.6)并结合(2.4)式得搜索方向(∆x,∆s,∆y),令

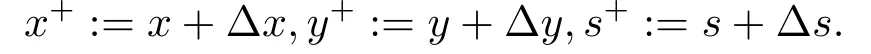
步4 由下面的(4.1)式求得θ ∈(0,1),令

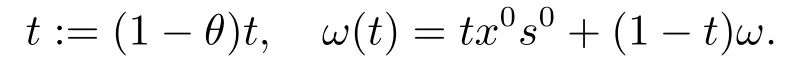
置k:=k+1.转步2.

3.算法分析

引理3.1若δ(υ)<1,则(x+,y+,s+)∈F0.

证令α ∈[0,1],记

由(2.4),(2.8)式和方程组(2.6)得

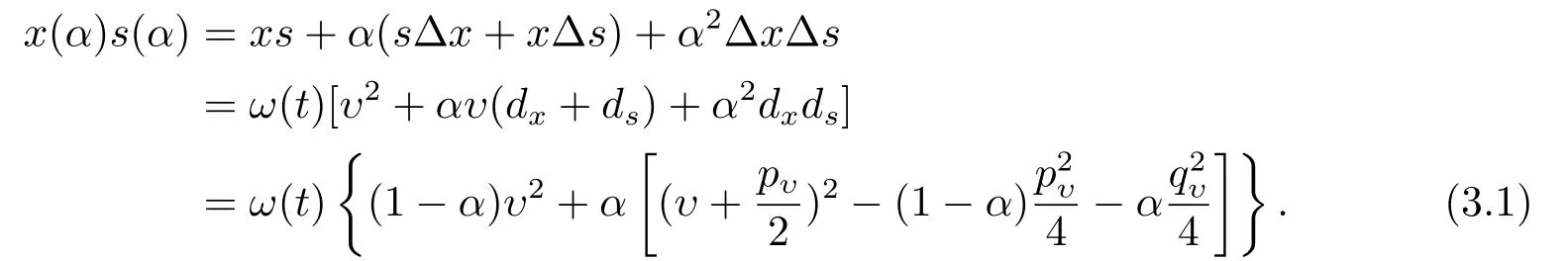
因为ω(t)>0,(1−α)υ2≥0,所以由(3.1)式知,若

则x(α)s(α)>0.由(2.7)和(2.9)式,及δ(υ)<1可知

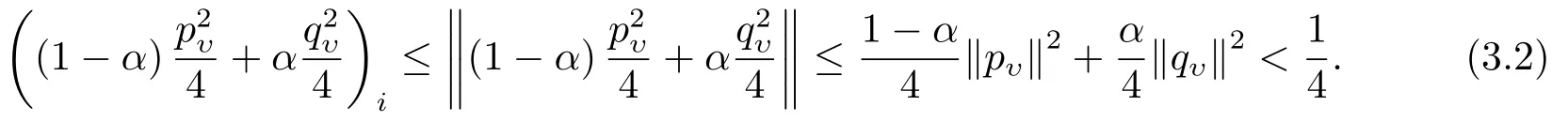
又由(2.7)式和引理2.2得

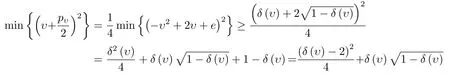
当δ(υ)<1时,由(3.3)式得

因此若δ(υ)<1时,则由(3.1),(3.2)和(3.4)式可得x(α)s(α)>0.

由于x(0)=x>0,s(0)=s>0且x(α),s(α)与α呈线性关系,所以对α ∈[0,1]有x(α),s(α)>0,相应地,x(1),s(1)>0.证毕.

引理3.2令,则

证由(3.1)式和引理2.2得

令f(η)=η2+η −η3.由f′(η)=2η+1−3η2=−(3η+1)(η−1)知,f(η)在(0,1)为单调递增函数.故由f(η)≤f(1)=1,η ∈(0,1)可得

因此,由(2.10),(3.5)和(3.6)式,得

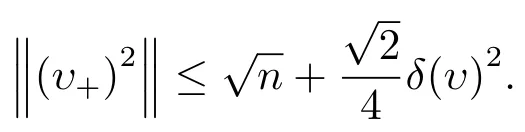
引理3.3令若δ(υ)<1,则

证由(2.6),(2.8)和(3.1)式得

因为δ(υ)<1,所以由引理2.2可得

由(2.7),(2.8),(2.9),(3.7)和(3.8)式知,当δ(υ)<1时有

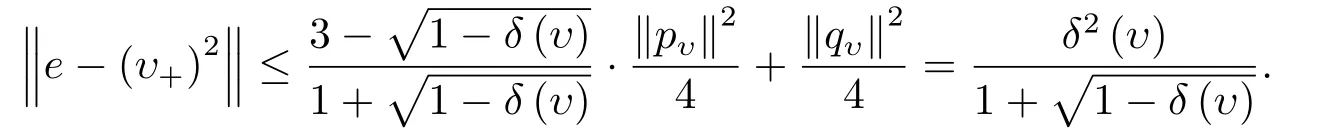
引理3.4令,则

证因为ω(t+)=ω(t)+θt(ω −x0s0),所以

故由引理3.3得

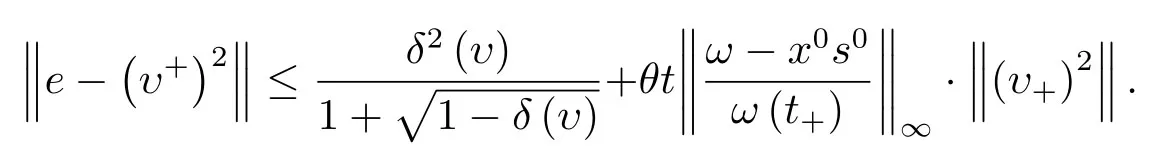
引理3.5令则

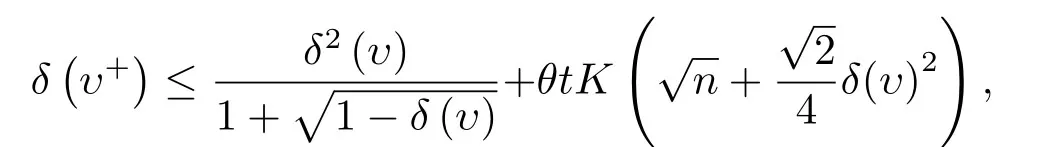
证由引理3.2和引理3.4得

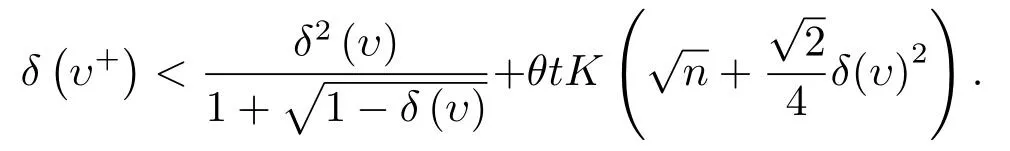
引理3.6给定常数β ∈(0,1),令若δ(υ)≤βt,则δ(υ+)<βt+.

证由引理3.5得

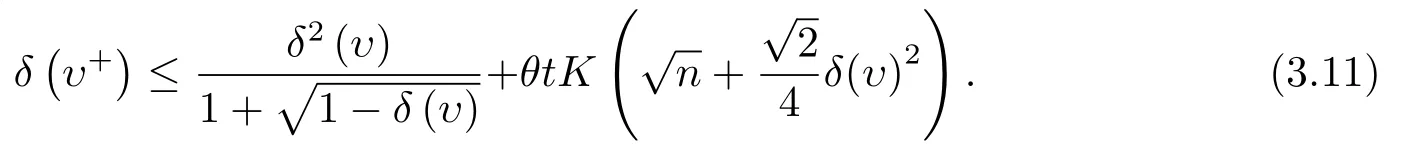
因为(3.11)式右端函数关于δ(υ)单调增加,所以若δ(υ)≤βt,则

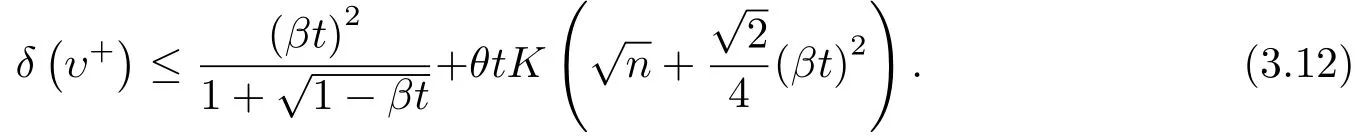
不妨设

其中t+=(1−θ)t,θ ∈(0,1)化简(3.13)式得

即

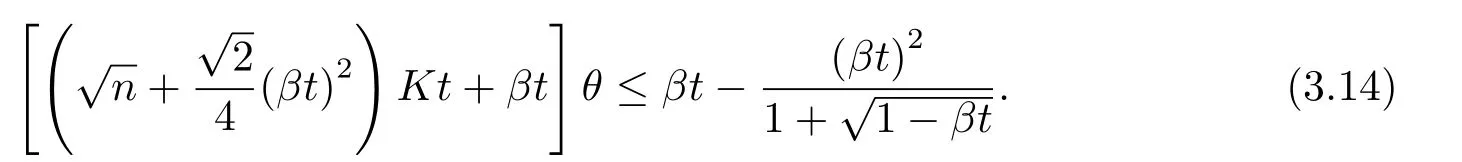
因为β ∈(0,1),所以故由式(3.14)得

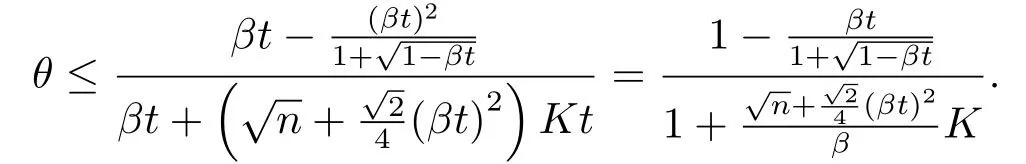
4.复杂度分析

选取参数β ∈(0,1),t ∈[0,1],令

因为t0= 1,则ω(t0)=x0s0,故δ(υ0)= 0<βt0.又t+= (1−θ)t,由引理3.1和引理3.6可知下一迭代点(x+,y+,s+)严格可行且δ(υ+)<βt+.

引理4.1设参数θ,K按(4.1)式选取.若δ(υ)≤βt,则

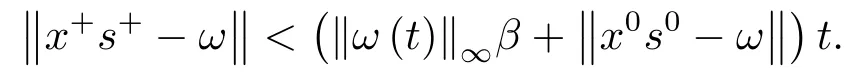
证由引理3.3得

因为β ∈(0,1),t ∈[0,1]所以若δ(υ)≤βt,则

引理4.2设参数θ,K按(4.1)式选取.若LWCP(2.1)存在最优解,则算法2.1至多经过

次迭代得到LWCP(2.1)的ε-近似解.

证因为∥ω(t)∥∞≤max{max(x0s0),max(ω)},所以由引理4.1可得

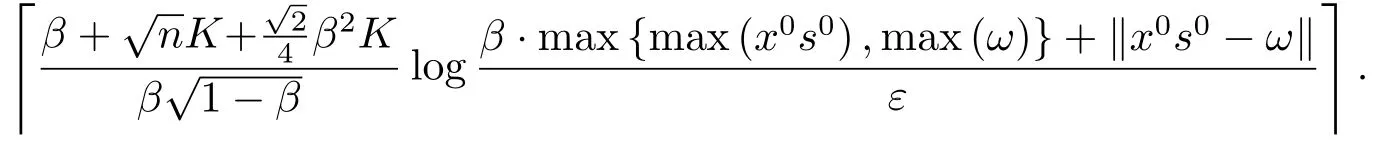
5.数值算例

为检验算法2.1的有效性,在Intel(R)Core i5 CPU2.3GHz 8.0内存,IOS操作系统的计算机上运用MATLABR 2016b编程进行数值实验.

在算法2.1中令参数t0= 1,ε= 10−5.随机生成5个不同规模的LWCP,且每种规模产生10个问题,分别取β= 0.7,β= 0.8和β= 0.9进行求解.随机生成行满秩矩阵A ∈Rm×n.选取任意起始点(x0,y0,s0)∈F0,权向量ω >0,按照(4.1)式选择参数θ,K.算法的终止准则为∥xs −ω∥≤ε,记Gap=∥xs −ω∥.如表5.1,5.2所示,在算法2.1求解相同规模的LWCP时K值上界与迭代次数和运行时间呈正相关关系.在K值上界确定的情况下,m和n对运行时间和迭代次数也有较大影响;从数值试验结果可知,在t从1减少到0的过程中,θ单调递增,且β的取值越趋向1,算法2.1求解同一LWCP所需的迭代次数就越少.表中数据均为求解不同规模的LWCP10次结果的平均值.

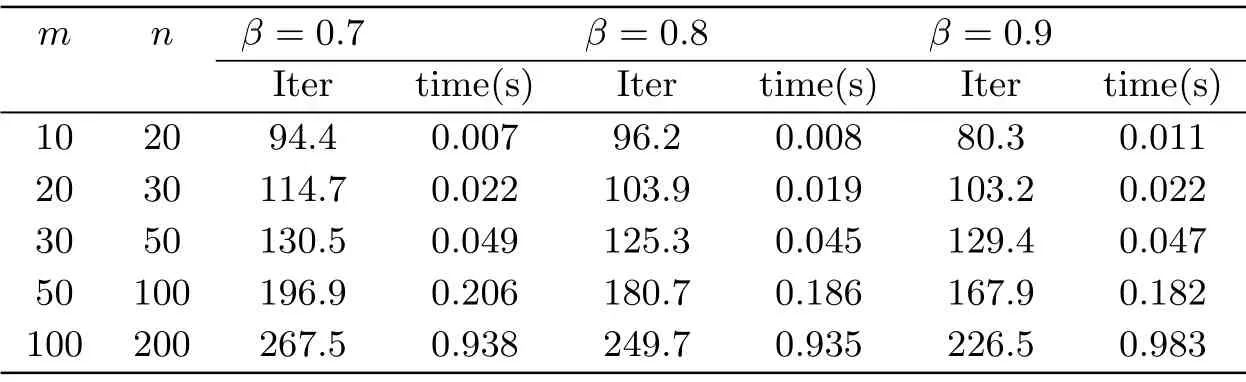
表5.1 K ≤2时求解不同规模和β值的LWCP的数值结果

表5.2 K ≤0.5时求解不同规模和β值的LWCP的数值结果

例5.1考虑R6上的LWCP(2.1),其中

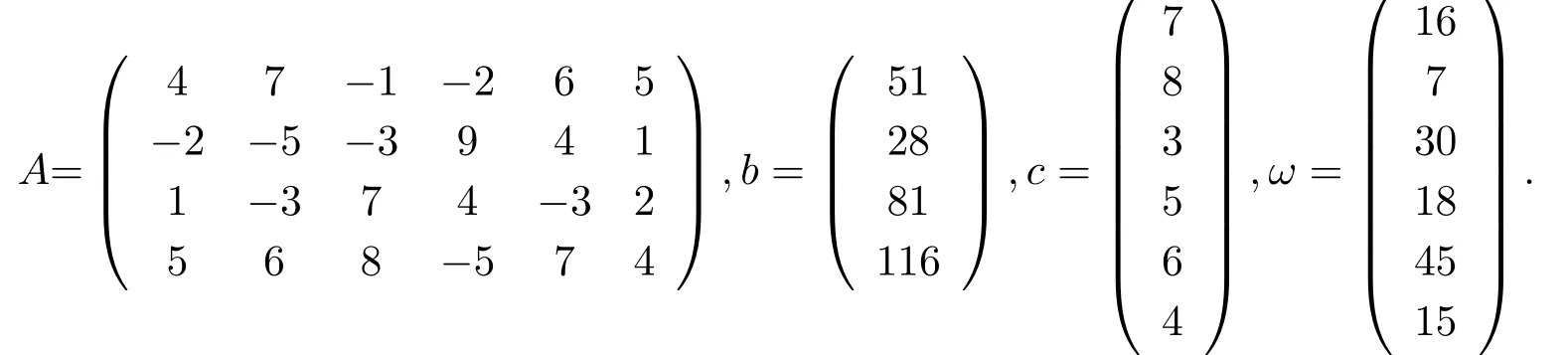
取初始点x0= (2,1,11,5,7,3)T,y0= (0,0,0,0)T,s0= (7,8,3,5,6,4)T,t0= 1,β=0.9.用算法2.1求解例5.1,得到最优解x∗= (2.100,0.738,10.986,4.836,7.105,3.092)T,y∗=−(0.141,0.109,0.035,0.026)T,s∗=(7.618,9.486,2.731,3.722,6.334,4.851)T.图5.1 可知,随着t的减小,Gap逐渐减小并趋于0,且每步迭代邻近测度都小于βt.

图5.1 迭代过程中邻近测度及Gap的值