非强制混合向量变分不等式解的存在性研究
2021-04-16许可范江华
许可,范江华
(广西师范大学数学与统计学院,广西 桂林541006)
1.引言
变分不等式及其应用是非线性分析中的重要部分,在力学,博弈论,经济,最优化理论和非线性规划等领域都有广泛应用.向量变分不等式是变分不等式的重要分支,向量变分不等式最早由Giannessi在文[1]中对有限维欧氏空间引入,大量学者对向量变分不等式进行深入研究并将其推广至无限维空间,参见文[2]及其参考文献.Lee和Bu[3]讨论了具有非紧多面体约束集和正半定矩阵的仿射向量变分不等式的解集的有界性和连通性.
人们对无界集上变分不等式问题加上强制性条件,使得解集非空有界.对于非强制变分不等式问题,例外簇方法是研究无界集上变分不等式问题解的存在性的有效方法.Smith[4]在Rn中首先利用例外序列研究非线性互补问题解的存在性;ZHAO[5]应用例外簇研究变分不等式问题;韩继业等人[6]给出变分不等式问题新的例外簇,得到解的存在性的一些新结果;王敏等[7]对Banach空间中变分不等式的例外簇,严格可行性及解的存在性三者之间的关系进行了研究.ZHONG等[8]提出了凸优化问题例外族,得到了自反Banach空间中凸优化问题的一些存在性结果,并应用于约束优化问题和凸二次规划问题.HUANG等[9]利用例外簇方法研究张量互补问题解的存在性,WANG等[10]利用例外簇方法研究张量变分不等式问题解的存在性.
本文以下设X为自反Banach空间,K为X的非空闭凸子集,设T:X →L(X,Rm),H:K →Rm为向量值映射,我们考虑如下形式的混合向量变分不等式MVVI(T;H;K):找到¯x ∈K使得
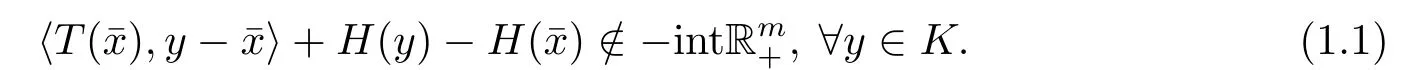
当m=1时,MVVI(T;H;K)为混合变分不等式.
对任一ξ ∈Rm+{0},定义ξH:K →R,使得ξH(x)=ξ(H(x)),我们考虑如下混合标量变分不等式:找到¯x ∈K使得
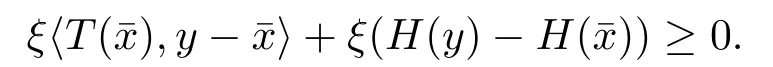
混合向量变分不等式是一类较为广泛的数学模型,包含了变分不等式问题,优化问题及向量变分不等式问题,尚未有文献给出向量变分不等式问题的例外簇.另一方面,最近文[11]给出混合变分不等式解集为非空紧致集的充分条件.
本文利用例外簇方法研究非强制混合向量变分不等式的弱有效解的存在性;首先证明若混合向量变分不等式问题不存在例外簇,则混合向量变分不等式问题的弱有效解集为非空集合;利用向量值映射的渐近映射给出自反Banach空间中非强制混合向量变分不等式的弱有效解集不存在例外簇的充分条件,从而得到混合向量变分不等式问题的弱有效解的存在性结果;我们研究了当算子为余正仿射算子时,给出混合仿射向量变分不等式不存在例外簇的充分条件,得到混合仿射向量变分不等式弱有效解的存在性,还给出了混合向量变分不等式的弱有效解集为非空紧致集的充分条件.将文[11]中有限维空间中标量混合变分不等式解的存在性结果推广到自反Banach空间中混合向量变分不等式.
2.预备知识
本节给出本文需要的基本定义和结论.
设X为自反Banach空间,X∗为X的对偶空间.K为X中非空闭凸子集,K的内部,边界和闭包分别用intK,∂K和来表示.我们用∥·∥表示X中的范数.”→”,”⇀”分别表示强收敛和弱收敛.
我们用coneK:=∪t≥0tK为K生成的锥.给定锥P ⊂X,称紧凸集B0为P的一个紧致基,若0/∈B0,且P= coneB0.一个有紧致基的锥被称为具有良好基,显然有限维空间中闭凸点锥具有良好基.给定ε>0,定义Pε=cone(B0+B(0,ε)),显然Pε是锥,且P ⊆Pε.
定义K的退化锥
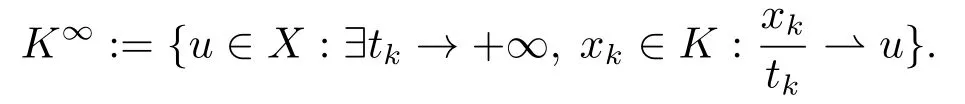
当K是闭凸集时,有
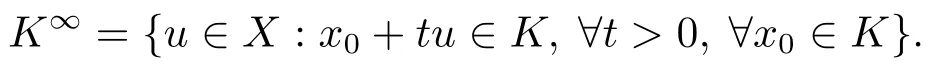
并且K∞也是凸集.
定义K的障碍锥
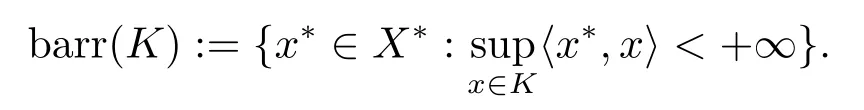
定义2.1函数f:K →R称为凸函数,若满足对任意的x,y ∈K,t ∈[0,1],有
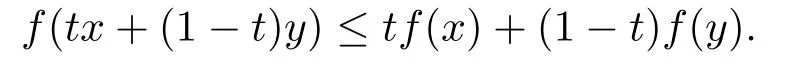
定义2.2F:K →Y称为Rm+-凸向量值映射,若对任意的x,y ∈K,t ∈[0,1],有
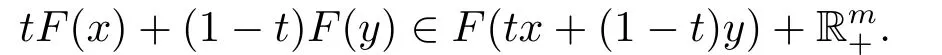
定义2.3设X为Banach空间,D(T)⊂X,算子T:X →L(X,Rm),
1)称T在x0∈D(T)处强连续,若
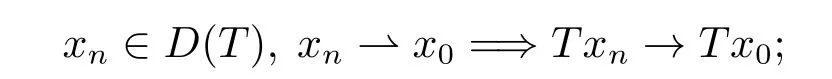
2)称T为1 次正齐次,若对任一x ∈D(T),任一λ>0,有T(λx)=λT(x).
定义2.4设F:K →Rm为非空向量值映射,则称F:
(i)在点x0是Rm+-上半连续,如果对Rm中零点的任意开邻域V,存在x0在X中的开邻域U,对任意的x ∈U,有F(x)∈F(x0)+V −Rm+;
(ii)在点x0是Rm+-下半连续,如果对Rm中零点的任意开邻域V,存在x0在X中的开邻域U,对任意的x ∈U,有F(x)∈F(x0)+V+Rm+.
设F:X →Rm为向量值映射,F=(f1,...,fm),由Rm+-凸映射与Rm+-下半连续映射的定义可知
1)若F:X →Rm为Rm+-凸映射,则对任一i ∈{1,...,m},fi:X →R为凸函数;
2)若F:X →Rm为Rm+-下半连续映射,则对任一i ∈{1,...,m},fi:X →R为下半连续函数.
定义2.5给定矩阵A ∈Rn×n,我们称
1)A是正定矩阵,若对于所有x ∈Rn,当xθ时,有(Ax,x)>0;
2)A是半正定矩阵,若对于所有x ∈Rn有(Ax,x)≥0;
3)A是K-余正矩阵,若对于所有x ∈K有(Ax,x)≥0;
4)A是K-余正+矩阵,若对于所有x ∈K有(Ax,x)≥0.当(Ax,x)= 0意味着Ax= 0,x ∈K.
显然,正定矩阵都是半正定的,半正定矩阵在Rn的非空子集K上都是K-余正矩阵.反之则通常不成立.
定义2.6设h:Rn →R ∪{+∞}是真函数,h∞:Rn →¯R:=R ∪{±∞}称为h的渐近函数,若
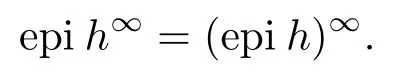
并且有如下等式:
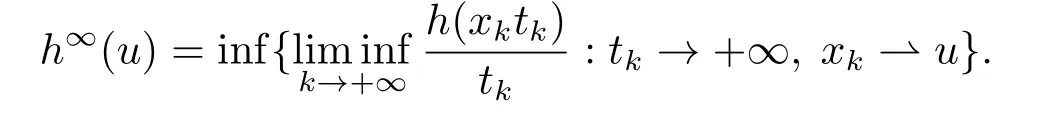
当h是真凸下半连续函数时:
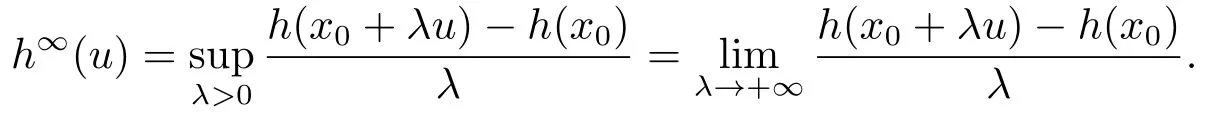
文[12]定义向量值映射的渐近映射如下.
定义2.7[12]设F:X →Rm为向量值映射,称F∞:X →Rm为F的渐近映射,若
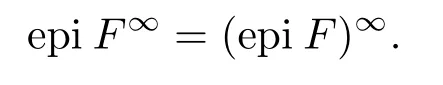
定义2.8任意给定称序列{xr}r>0为混合向量变分不等式问题MVVI(T;H;K)相对于的例外簇,若
1)xr ∈K,且
2)对任一y ∈Kr,有
引理2.1[13]设K是X的非空闭凸子集,若int(barr(K))∅,则不存在满足∥xn∥→∞的序列{xn}⊂K,使得
我们容易证明如下引理.
引理2.2设C为线性赋范空间Y中的闭凸点锥且intC∅,则
1)C+Y (−intC)⊂Y (−intC);
2)intC+C=intC;
3)C ⊂Y (−intC).
下面引理说明若K为有界闭凸集,则MVVI(T;H;K)的弱有效解集S(T;H;K)为非空集合.
引理2.3设K为自反Banach空间X的非空有界闭凸子集.设T:X →L(X,Rm)是强连续映射,H:X →Rm是真Rm+-凸,Rm+-下半连续映射.则MVVI(T;H;K)的弱有效解集S(T;H;K)为非空集合.
证任取ξ ∈Rm+{0},考虑如下标量平衡问题:找到x0∈K使得
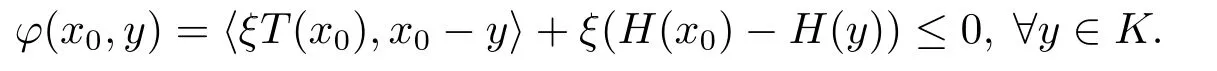
下证上述标量平衡问题在K上有解.
设τω为X上的弱拓扑,因为K为X中有界闭凸集,故K为(X,τω)中紧凸集.显然对任意的x ∈K,φ(x,y)关于y是凹的,对任意的y ∈K,φ(x,y)关于x是下半连续的.由Ky Fan极大极小不等式定理知,存在x0∈K使得
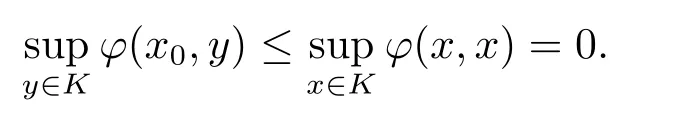
即有
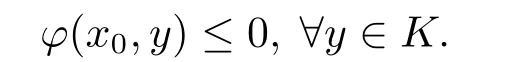
显然x0为MVVI(T;H;K)的弱有效解,从而S(T;H;K)为非空集合.
引理2.4[14]设X为自反Banach空间,设对于任一i ∈{1,...,m},fi:X →R为下半连续凸函数,则
下面引理给出向量值映射的渐近映射的性质.
引理2.5设F:X →Rm为Rm+-凸,Rm+-下半连续映射,F= (f1,...,fm).则对任一ξ ∈Rm+{0},任一d ∈dom(F∞),有(ξF)∞=ξF∞.
证因任一i ∈{1,...,m},fi:X →R为下半连续凸函数,任一ξ ∈Rm+{0},因ξi ≥0,由引理2.4,有故有(ξF)∞=ξF∞.
3.混合向量变分不等式解的存在性
本节首先在定理3.1中证明混合向量变分不等式的弱有效解集为空集则存在例外簇.推论3.1说明若不存在例外簇,则混合向量变分不等式问题的弱有效解集为非空集合.在定理3.2中,我们利用Rm+-凸映射的渐近映射,给出条件使得混合向量变分不等式不存在例外簇,证明了混合向量变分不等式问题的弱有效解集为非空有界集.我们将文[11]的部分结果推广到自反Banach空间中混合向量变分不等式情形.
定理3.1设K为自反Banach空间X的非空闭凸子集,∈K.设T:X →L(X,Rm),设H:X →Rm是真Rm+-凸,Rm+-下半连续映射.若混合向量变分不等式问题MVVI(T;H;K)无解,则存在序列{xr}r>0为混合向量变分不等式问题MVVI(T;H;K)相对于的例外簇.
证由引理2.3知,存在xr ∈Kr,使得xr为问题MVVI(T;H;Kr)的解,即
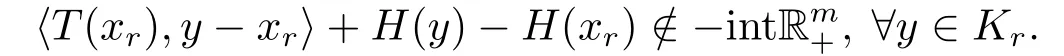
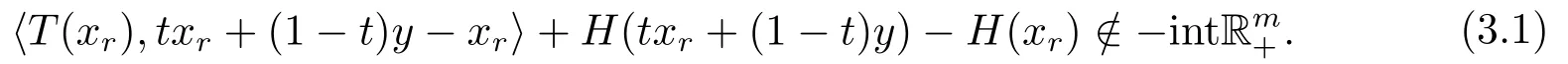
因H为Rm+-凸映射,tH(xr)+(1−t)H(y)∈H(txr+(1−t)y)+Rm+,故
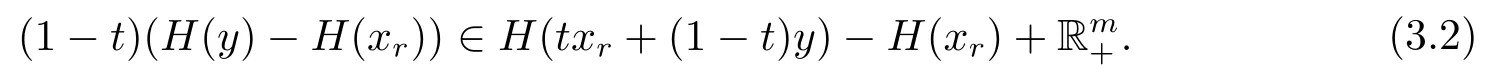
将(3.2)代入(3.1)得
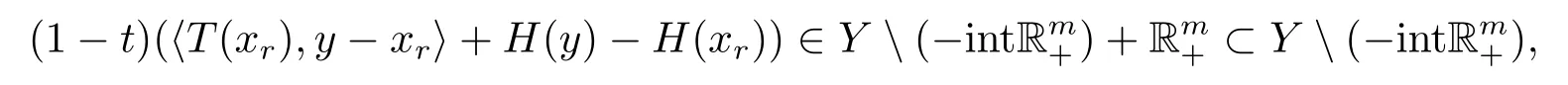
故有
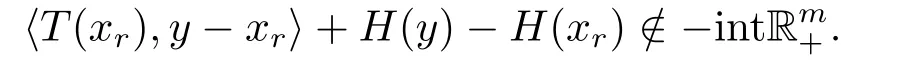
从而xr为问题MVVI(T;H;K)的解,与定理3.1条件混合向量变分不等式问题MVVI(T;H;K)无解矛盾.故∥r −∥=r,从而{xr}r>0为混合向量变分不等式问题MVVI(T;H;K)相对于的例外簇.
下面推论3.1说明不存在例外簇,则混合向量变分不等式问题的弱有效解集为非空集.推论3.1为定理3.1的逆否命题.
推论3.1设K为自反Banach空间X的非空闭凸子集,∈K.设T:X →L(X,Rm),设H:X →Rm是真Rm+-凸,Rm+-下半连续映射.若混合向量变分不等式问题MVVI(T;H;K)不存在相对于的例外簇,则问题MVVI(T;H;K)的弱有效解集S(T;H;K)为非空集.
定理3.2设K为自反Banach空间X的非空闭凸子集且int(barrK)∅,设T:X →L(X,Rm)为1 次正齐次的强连续映射,且对任意的x ∈K,满足⟨Tx,x⟩ ∈Rm+.设H:X →Rm是真Rm+-凸,Rm+-下半连续映射,且存在x0∈K使得
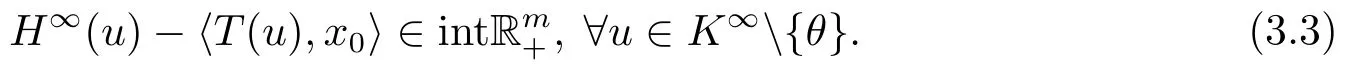
则S(T;H;K)为非空有界闭集.
证首先证明S(T;H;K)为非空集.假设S(T;H;K)=∅.
对任意y ∈K,存在r0>0,满足r0>∥y∥,有
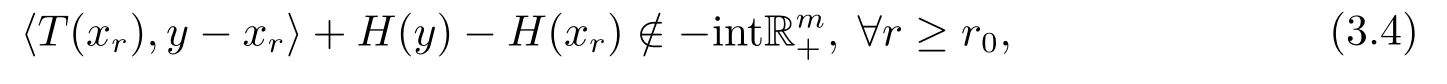
即
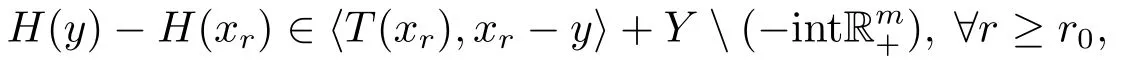
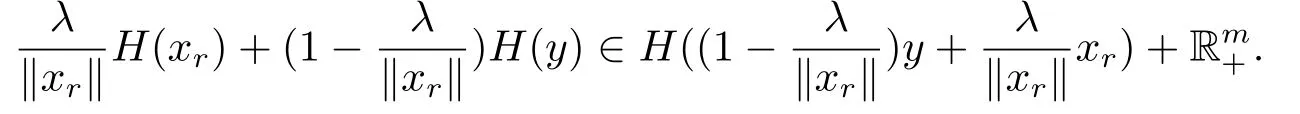
从而有
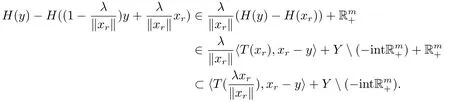
因对任意x ∈K满足得
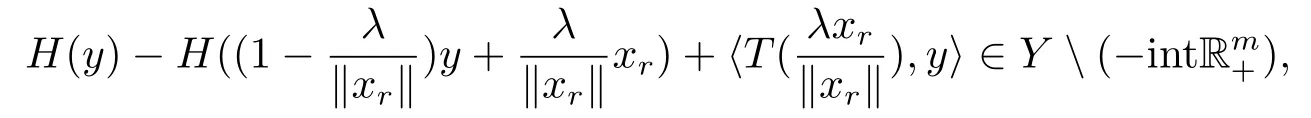
则存在ξ ∈Rm+{0},使得
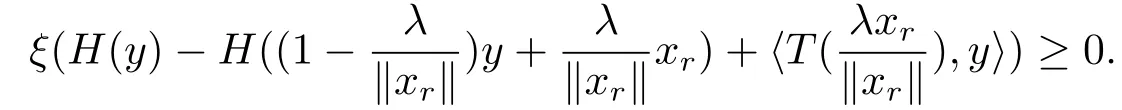
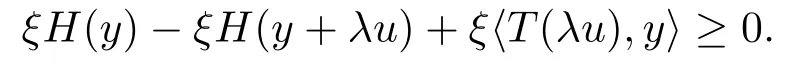
因ξH为真凸下半连续函数,由真凸下半连续函数的渐近函数定义可知,存在.故即由引理2.5知,(ξH)∞=ξH∞,从而故有
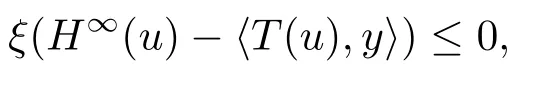
因此
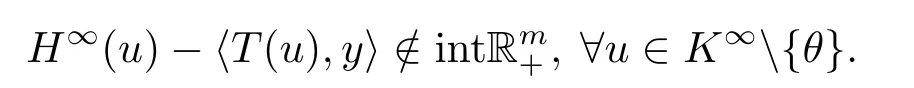
与定理3.2条件矛盾.从而S(T;H;K)∅.
下面用反证法证明S(T;H;K)为有界集.假设存在{xn}∈S(T;H;K),使得∥xn∥=+∞.
因为supn∈N∥xn∥= +∞,知重复上述证明过程可得到矛盾.故S(T;H;K)为有界集.
下面证明S(T;H;K)为闭集.任取{xn}⊂S(T;H;K),且xn →x0.因{xn}⊂S(T;H;K),故有
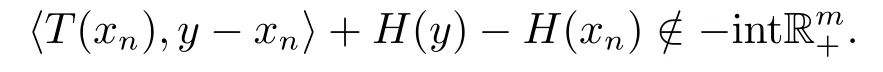
故存在ξ ∈Rm+{0},使得
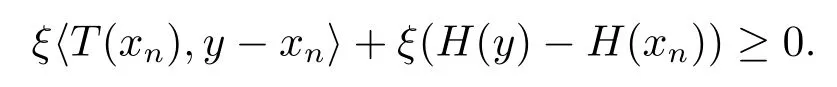
上式两侧取下极限,得
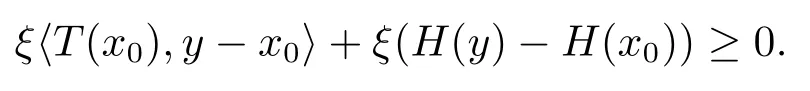
从而有
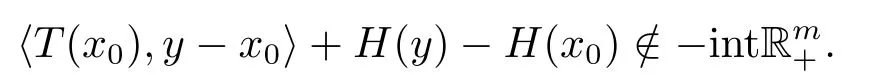
所以x0∈S(T;H;K),因此S(T;H;K)为闭集.
注3.1当X为有限维欧氏空间,m= 1时,文[11]得到了混合变分不等式解集为非空紧致集的充分条件.定理3.2将文[11]部分结果推广到自反Banach空间中混合向量变分不等式.
4.混合仿射向量变分不等式弱有效解的存在性
本节研究如下混合仿射向量变分不等式MAVVI(A;H;K),找到x0∈K使得
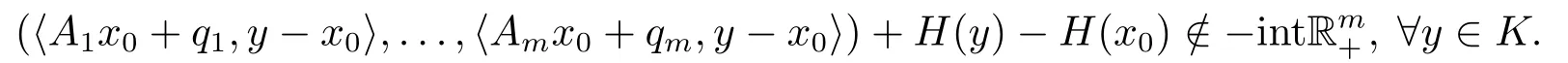
其中Ai ∈Rn×n,Ai ∈Rn×n为K-余正矩阵,qi ∈Rn,i= 1,...,m;H:Rn →Rm为Rm+-凸,Rm+-下半连续映射,H= (h1,...,hm).因此对每个i ∈{1,...,m},hi为真凸下半连续函数.称x0为MAVVI(A;H;K)的弱有效解,记S(A;H;K)为MAVVI(A;H;K)的弱有效解集.
在定理4.1中,我们将定理3.2的结果应用到混合仿射向量变分不等式,得到混合仿射向量变分不等式的弱有效解集为非空紧致集的充分条件.在定理4.2中,我们给出混合仿射向量变分不等式不存在例外簇的充分条件.
定理4.1设K为Rn中的非空闭凸子集,设H:Rn →Rm为Rm+-凸,Rm+-下半连续映射,对任一i ∈{1,...,m},Ai ∈Rn×n为K-余正矩阵,qi ∈Rn,若存在x0∈K使得
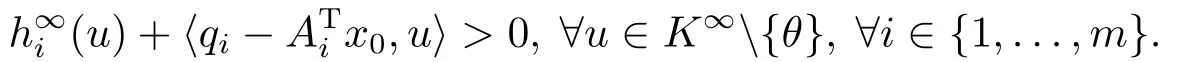
则MAVVI(A;H;K)的弱有效解集S(A;H;K)为非空紧致集.
证因H:Rn →Rm为Rm+-凸,Rm+-下半连续映射,故对任一i ∈{1,...,m},hi为真凸下半连续函数.定义G:Rn →Rm,使得G(x)=H(x)+qx,即gi(x)=hi(x)+qix.令T(x)=(A1x,...,Amx),根据G的定义,有
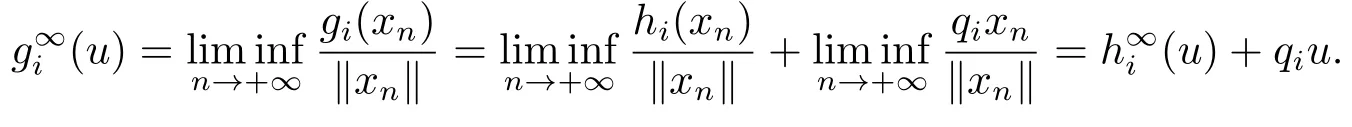
由已知条件知
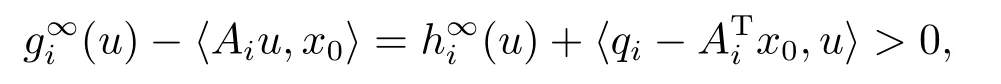
因此
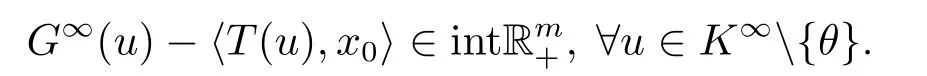
由定理3.2知,对任意y ∈K,存在x0∈K使得
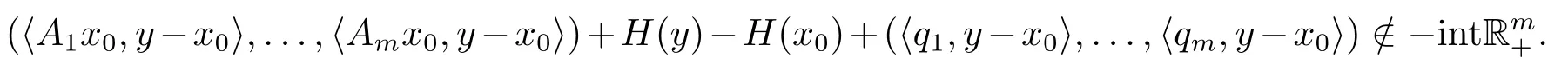
故S(A;H;K)为非空有界闭集,又因Rm为有限维空间,故S(A;H;K)为非空紧致集.
若K为闭凸集,则K∞是闭凸锥.若K∞具有良好基,给定ε>0,我们定义K∞ε=∪t≥0t(K∞+εB(0,1)).
定理4.2设K为Rn中的非空闭凸子集,K∞具有良好基.对任一i ∈{1,...,m},设Ai ∈Rn×n是K∞ε-余正+矩阵.设H是Rm+-凸,Rm+-下半连续映射,且有
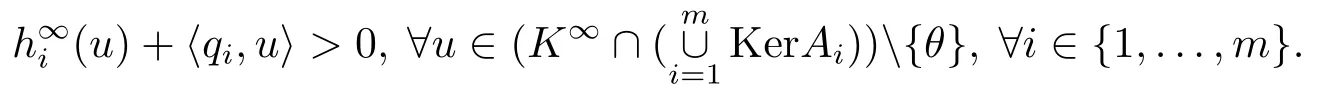
则MAVVI(A;H;K)的弱有效解集S(A;H;K)为非空紧致集.
证首先证明S(A;H;K)为非空集.假设S(A;H;K)=∅.
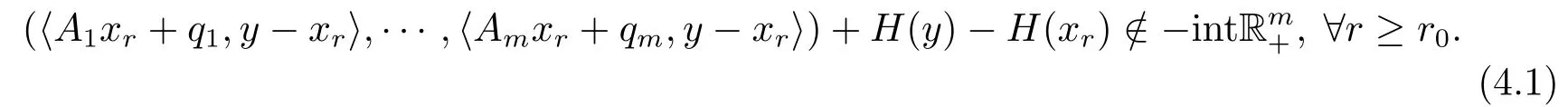
由(4.1)知,存在i0∈{1,...,m},存在{xr}r>0的子序列,不失一般性,仍记为{xr}r>0,使得
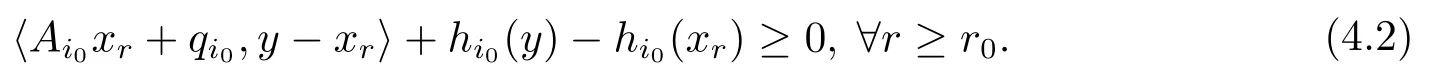
两侧除以∥xr∥2,得
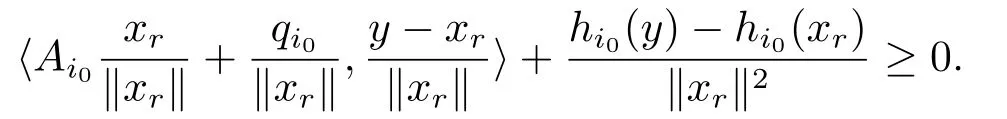
两边取下极限,且因hi0为凸函数,有从而有
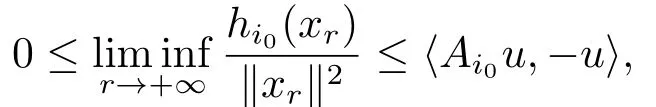
在(4.2)式中除以∥xr∥,得
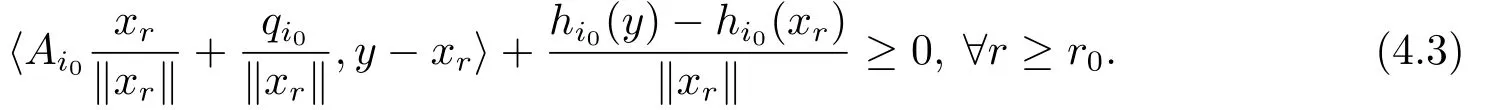
因为Ai0是K∞ε-余正+矩阵,故当r充分大时,有从而
(4.3)式可写为
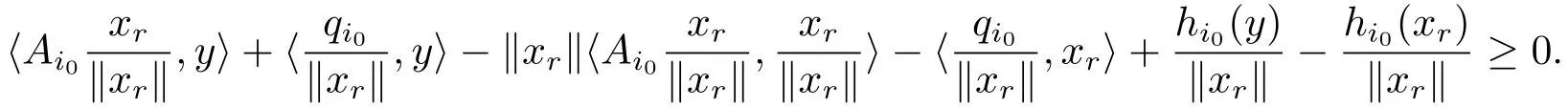
故有
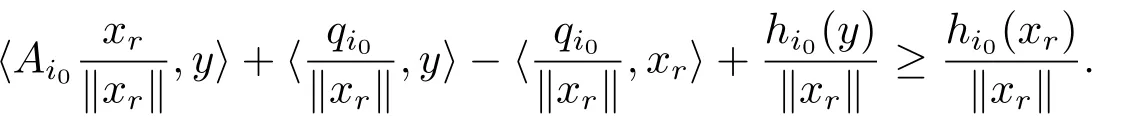
令r →∞,上式两边取下极限,则有又因为u ∈KerAi0,故
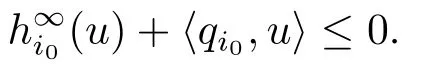
与已知条件矛盾,故S(A;H;K)为非空集.
利用定理3.2的证明方法,可得S(A;H;K)为非空有界闭集,故为Rn中非空紧致集.
例4.1设X= R2,Y= R2.H= (h1,h2),其中则H为R2+-凸,R2+-下半连续映射,A1,A2是K-余正矩阵,且K∞={(x1,x2)∈R2+:且K∞有紧凸基{(x1,x2)∈R2+:故K∞具有良好基.T(x)= (A1x,A2x),对任一x ∈K,对任意u ∈K∞{θ},有h∞1(u)=h∞2(u)=+∞.满足定理3.2,定理4.1,定理4.2的条件.
