基于组LASSO的重组近亲杂交合作小鼠基因位点定位研究
2021-04-16熊思灿胡桂开阮周生
熊思灿,胡桂开,阮周生
(东华理工大学理学院,江西 南昌330013)
1.引言
杂交合作(Collaborative Cross,CC)小鼠计划于2004年正式提出[1],它由具有不同性状的八个基本(founder)小鼠品系近亲杂交约20代形成.理论上,CC小鼠的基因型应该是纯合的(homozygous).实际中,当CC小鼠基因型中的纯合子比例达到98%及其以上时,便停止繁殖[2].此外,理论上,CC小鼠的每个位点具有等可能,即1/8的概率继承8个祖先中的任何一个.实际上,每个祖先的贡献可能不同[3].
重组近亲杂交(recombinant inbred intercrosses,RIX)实验是ZOU等于2005年为了克服重组近亲(recombinant inbred,RI)品系的不足之处,如样本量小等,而提出的.[4]基于RIX实验所得品系的数量性状位点定位(quantitative trait loci,QTL)功效会得到提高.当RIX实验的杂交小鼠选择为CC品系时,将会得到CC-RIX品系.CC-RIX品系具有很多CC品系以及RIX品系不具有的优点,它是一个可重复(reproducible)产生的杂合子(heterozygous)多亲群体,其基因变异与人类是相似的.[5]基于CC-RIX品系,已有部分研究,如GONG和ZOU[6]考虑了系数随时间变化而变化的时变非参数数量性状位点定位方法,Giusti-Rodríguez等[7]考虑了抑制精神病药物的副作用的遗传基础问题,Graham等[5]考虑了细胞免疫表型的遗传位点定位问题[5],LIU等[8]考虑了带亲源效应(parent-of-origin,PoO)和主基因效应的联合建模问题,并采用了分块Gibbs算法对模型进行求解.分块Gibbs算法属于贝叶斯(Bayesian)算法的一种,具有如整块更新,可减少收敛时间等优点.但当位点个数较大时,其计算量依然很大.
惩罚函数法作为高维数据处理的又一方法,往往具有运算速度快,收敛时间短等特点.如LASSO (least absolute shrinkage and selection operator)[9],SCAD (smoothly clipped absolute deviation)[10],adaptive LASSO[11],以及组LASSO(Group LASSO)[12]等.考虑到CCRIX的每个位点的基因型可能来自于八个祖先,若其中的某个或者某些祖先对应的效应非零,则表明该位点为数量性状位点.因此,基于CC-RIX品系的数量性状位点定位问题,本质上是一个组变量选择(group variable selection)问题.本文在文[8]模型的基础上,忽略亲源效应,考虑仅有主基因效应的数量性状位点定位模型,以及组LASSO惩罚函数求解算法.注意到本问题中的非光滑性(non-smoothness)以及不可分割性(non-separable),以及设计矩阵不满足部分正交性(partial orthogonal property),导致一些流行算法,如坐标下降(coordinate descent)算法不能直接使用.因此,本文采用了迭代加权最小二乘法(Iteratively Re-weighted Least-Squares,IRLS)进行模型求解,为基于CC-RIX品系的复杂性状位点定位提供参考.
2.模型建立
假设共有L个CC父系,将他们按照RIX实验的繁殖办法,可得n(≤L(L −1)/2)个CCRIX样本.对每个样本,假定其总的位点个数为p,且记其相应的表型(phenotype,即因变量)为yi,(i=1,··· ,n).在LIU等[8]所建立的混合线性模型(linear mixed model,LMM)基础上,忽略亲源效应后,可得如下仅含主基因效应的定位模型:
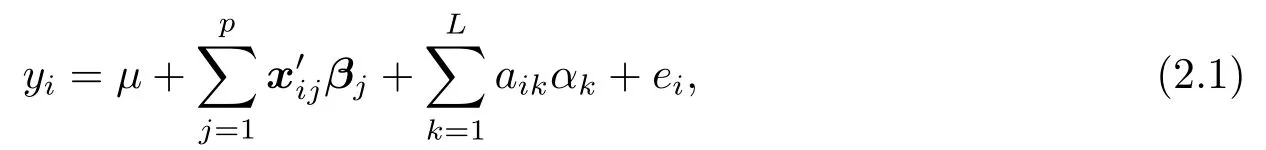
其中,µ,βj= (βj1,··· ,βj8)′以及αk分别表示总均值,主基因效应(即八个祖先的等位效应,founder allelic effect),以及随机多基因效应(random polygenic effect).xij=(xij1,··· ,xij8)T,当第i个CC-RIX样本,即CC-RIXi(i=1,2,··· ,n)在第j(j=1,2,··· ,p)个位点继承了第k(k=1,2,··· ,8)个祖先的0个,1个或者2个基因时,相应的xijk取0,1或者2.当第i个CC-RIX样本,即CC-RIXi(i= 1,2,··· ,n)由0个,1个或者2个父系CCk(k= 1,2,··· ,L)杂交形成时,相应的aik取0,1或者2.显然有,因为每个CC-RIX样本有且仅有2个父系.为方便描述,记矩阵A= (aik)n×L.按照文[8]中的假定,对随机效应项αk(k=1,2,··· ,L),我们依然假定αk ∼N(0,σ2a).其中,σ2a为多基因效应方差.同时,对随机误差项ei(i= 1,2,··· ,n),我们依然假定其独立同分布于正态分布,即ei ∼N(0,σ2e).其中,σ2e为随机误差方差.
令y= (y1,··· ,yn)T,µ=µ(1,··· ,1)T,x= (x1,··· ,xp),xj= (x1j,··· ,xnj)T,β=α=(α1,··· ,αL)T,以及e=(e1,··· ,en)T,则模型(2.1)可改写为

模型(2.2)在文[8]中的研究中,被用作比较模型.正如作者所述,当不存在亲缘效应时,该模型的表现是与含亲源效应的模型表现是相似的.因此,在只为探测主基因效应时,模型(2.2)不失为一个理想模型.接下来,本文重点从组LASSO惩罚函数法的角度来求解模型(2.2).
3.组LASSO方法
由随机多基因效应α ∼NL(0,σ2aIL),可得其概率密度函数为
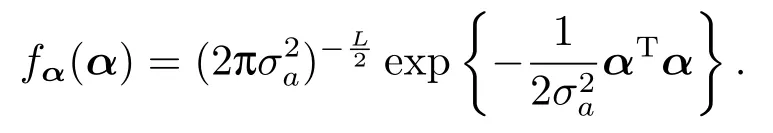
因此,给定α的条件下,y的条件分布为
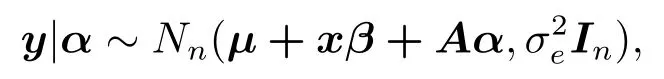
其相应的条件概率密度函数为
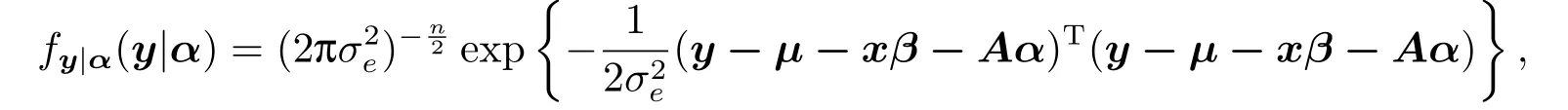
从而,伪数据(pseudo-data){(y,x,A,α)}的全似然函数为
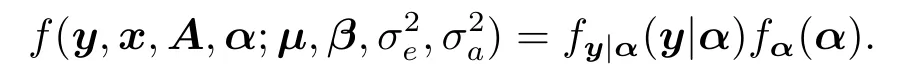
对随机效应项α1,··· ,αL进行积分,可得观测数据的似然函数为
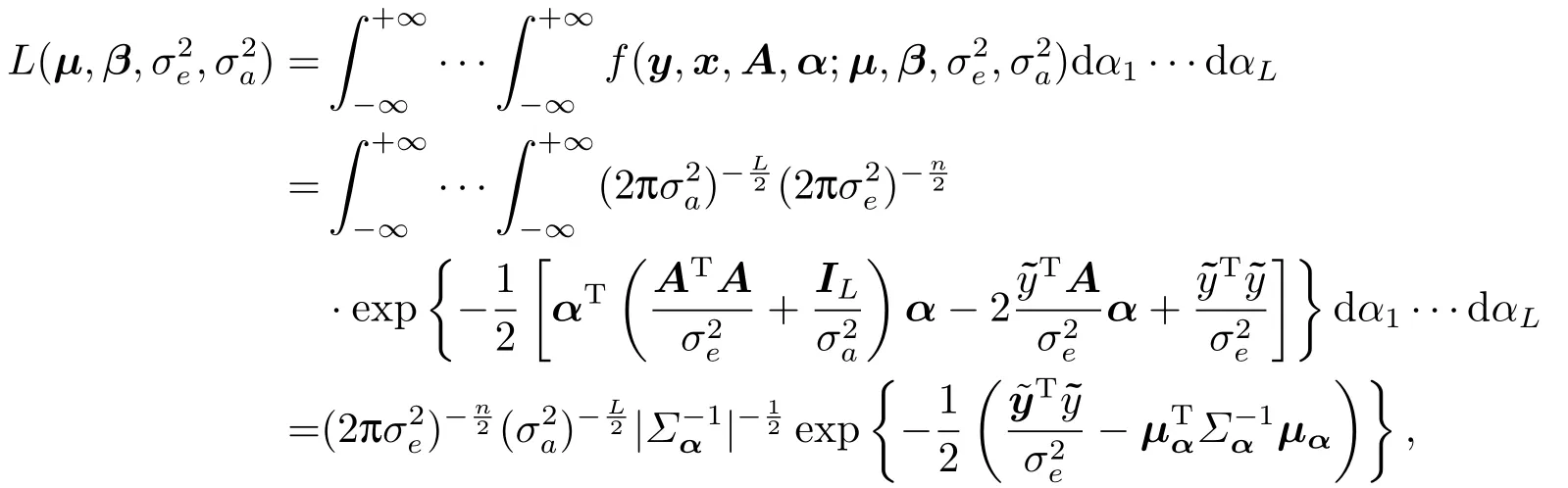
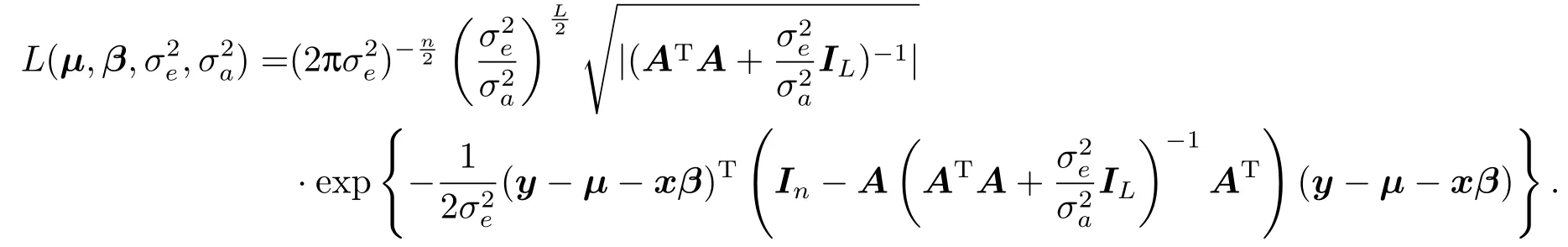
注意到
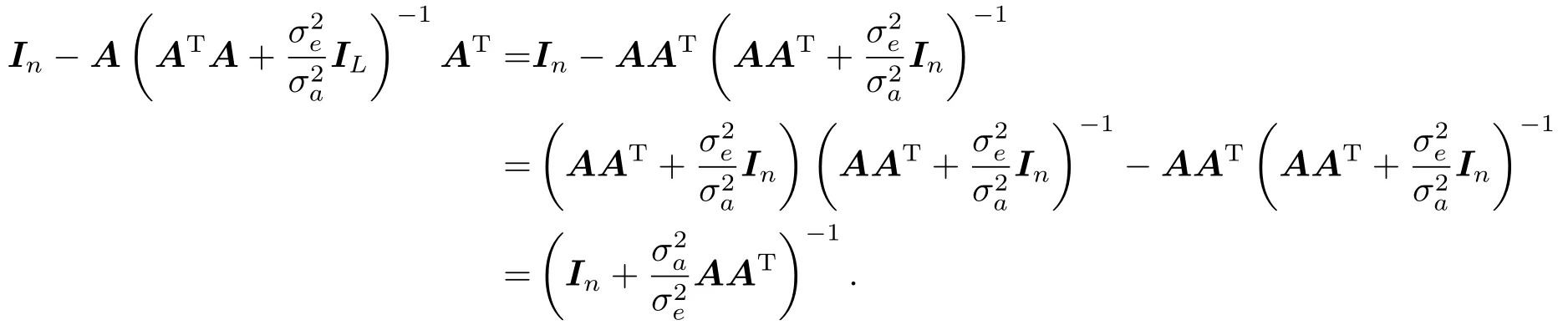
从而,似然函数可改写为

一般而言,因位点个数p远大于样本量n,即p ≫n,经典的极大似然估计法,以及限制极大似然估计法(restricted maximum likelihood approach)[13]将不再适用.注意到,尽管位点个数较大,但是真正起作用的却较少.因此,本文假定主基因效应,即β=(βT1,··· ,βTp)T满足稀疏性条件,也即大量的βj(j= 1,··· ,p)是为零的.考虑到βj= (βj1,··· ,βj8)T是一个8×1维向量,如果其中的部分分量不为零,则其对应的位点对表型存在显著性影响.因此,对CC-RIX 品系的数量性状位点定位问题本质上是组变量选择问题.为此,我们采用负对数似然函数,外加组LASSO惩罚函数的方法来获取主基因效应的稀疏解.求解的目标函数为:
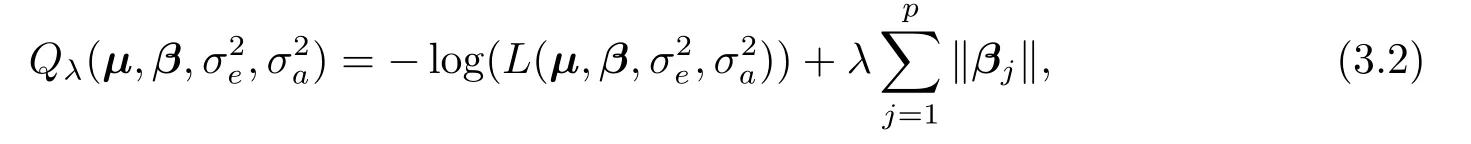
这里,λ为非负的正则化参数,∥βj∥= (βTj βj)1/2(j= 1,··· ,p)为βj的l2- 模.此处,我们采用l2-模表示主基因效应的分量要么全部为零,要么不全为零,以此实现组变量选择[12].当某个位点的主基因效应的所有分量全部为零时,相应的位点不是数量性状位点.否则,相应的位点为数量性状位点.参数的最优解可表示为如下最小化问题:
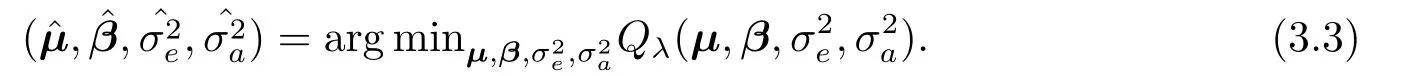
尽管最小化问题(3.3)对所有参数是一个非凸(non-convex)最优化问题,难于求解.不过,当固定µ,σ2e以及σ2a时,该问题为一个易于求解的凸最优化问题.注意到我们的主要目的是进行数量性状位点定位,其效应值的估计则变为次级目标.因此,我们将对轮廓对数似然函数(profile log-likelihood function),并采用迭代加权最小二乘法进行求解.
4.迭代加权最小二乘法
为了进行数量性状位点定位,我们对似然函数(3.1)取对数,并去掉其中的常数项,得到如下的以负轮廓对数似然函数表示的目标函数:
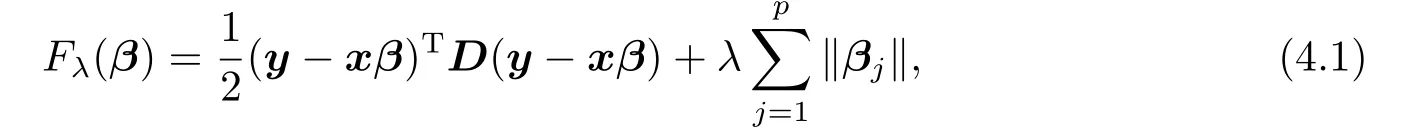
这里,且为了简化计算,我们将γ以及σ2e当成两个固定常数,这可以事先指定.这种等价替代(proxy)思想已被FAN等[14]研究过.他们指出,在一定的条件下,求解此等价替代问题依然能获得正确的模型选择结果,但可能会导致额外的估计偏差.本文,我们首先最小化(4.1)进行数量性状位点定位,然后采用限制极大似然估计法得到其他参数的估计值.为此,记γ以及σ2e的估计值为以及,矩阵D的相应估计值为.不失一般性,假定µ≡0.否则,我们可以用=(1n,x)和=(µ,βT)T分别替换x和β.
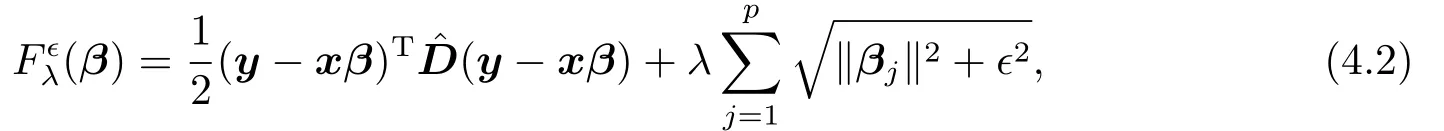
这里,ϵ>0为光滑化参数.之所以进行光滑化处理,其主要目的是可将等式(4.2)中的第二部分再次转换成β的二次型形式,从而便于构造迭代加权最小二乘法.
本文所研究的问题中,基因型矩阵x由0,1和2组成,容易导致矩阵xTx奇异.因此,标准的最优化方法,如牛顿−拉斐逊算法(Newton-Raphson algorithm)将不再适合.为此,本文提出一种迭代加权最小二乘法来求解问题(4.2)的最小值.
迭代加权最小二乘法是一种用于求解特定优化问题,如压缩感知(sparse recovery)[15],稳健回归(robust regression)等的常用方法.该方法是一个逐渐迭代的过程,其每一步更新都会求解一个加权最优化问题.假定在第k步迭代中,β的迭代值是β(k),其第k+1步的迭代值由下式给出:
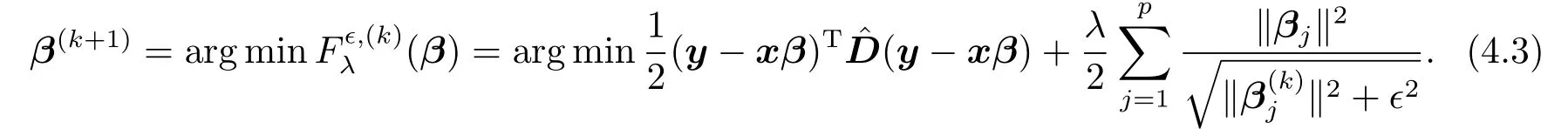
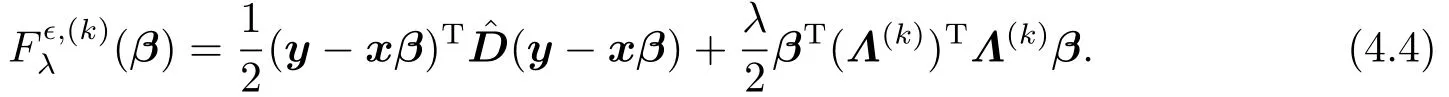
最小化(β)的必要条件是(β)对β的偏导数为零,即
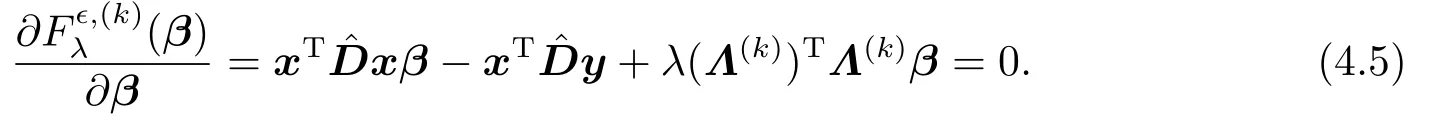
从而可得β(k+1)的显示表达,即
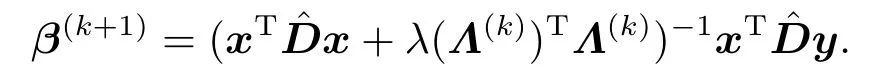
综合上述分析,当给定调节参数λ后,迭代加权最小二乘法的更新过程如下:
算法1(IRLS 算法)
步1 初始化参数:ϵ= 10−6,γ= 1,β(0)= (0,··· ,0)T,以及k= 0.计算
步2 按前述公式计算Λ(k);
步3 令k=k+1,计算
步4 重复步2和步3直到∥β(k)−β(k+1)∥<δ(=10−6)时,停止迭代.
上述迭代加权最小二乘法,除了第三步每次都需要基于新的Λ(k)值,计算一个8p×8p矩阵的逆矩阵之外,其余步骤的计算都能快速高效地完成.第三步中矩阵逆矩阵的计算可以使用乔里斯基分解(Cholesky decomposition)[16]来进行快速计算.因此,当迭代加权最小二乘法收敛时,记β的最优值为β(∗).而迭代加权最小二乘法的收敛性,将在接下来的一节中进行讨论.
5.迭代加权最小二乘法的收敛性
定理5.1假设{β(k)}∞k=1是由迭代加权最小二乘法产生的β的估计序列,则该序列的极限存在,且该极限值使得目标函数Fϵλ(β)达最小.
证众所周知,最小化Fϵλ(β)的迭代加权最小二乘法,等价于最小化如下辅助(auxiliary)函数[15]:
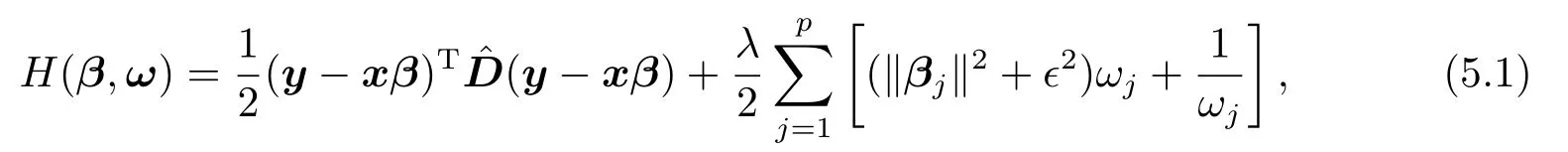
这里,ω=(ω1,··· ,ωp)T.在第k步迭代中,ω的值ω(k)由下式给出
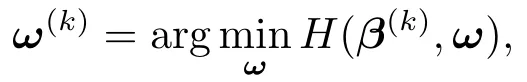
其中,β(k)为第k次迭代中β的估计值.易得,ω(k)的第j个分量
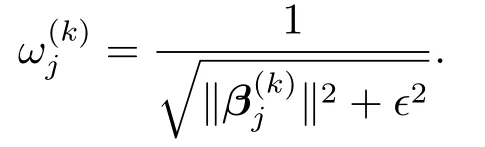
进而,再由式(4.3)可得第k+1步β的估计值为
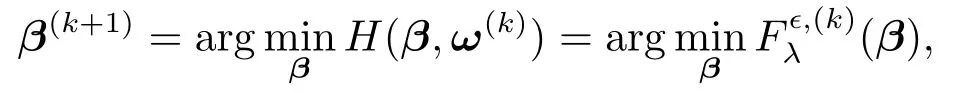
即最小化H(β,ω(k))和最小化等价,从而
注意到,如下不等式
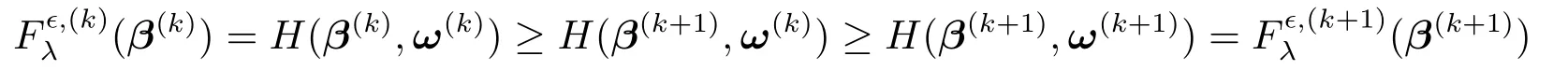
对任意的k ≥0成立,故迭代加权最小二乘法产生的序列是一个使得函数值单调不
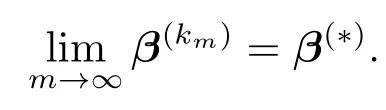
再由如下事实,

事实上,β(km+1)满足必要条件(4.5),即

从而,多次使用式(5.3)可得
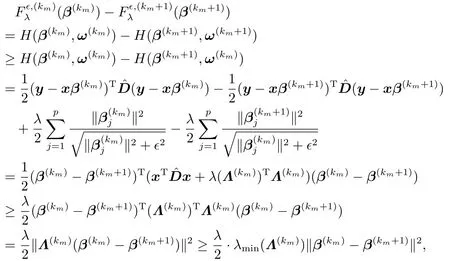
这里,λmin(Λ(km))是对角正定矩阵Λ(km)的最小特征值.将上述不等式两边分别关于m ≥1求和,再注意到从而有
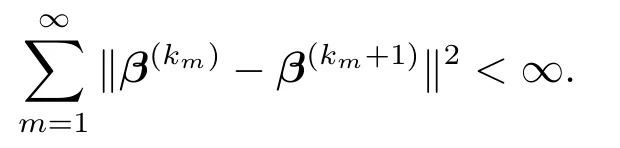
这将导出式(5.2).
对式(5.3)的两边分别关于m取极限,可得
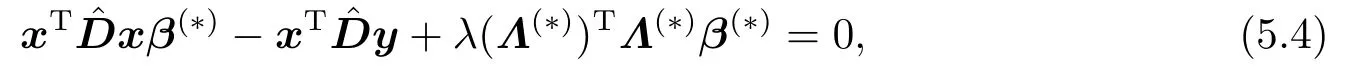
这里,是一个8p ×8p对角矩阵,且是一个8×8对角矩阵.注意到,由式(4.1)所定义的目标函数Fλϵ(β)是一个光滑的严格凸函数,其唯一的最小值点满足如下必要条件
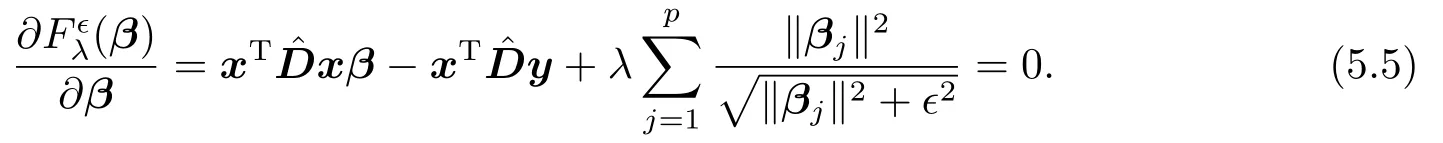
对比(5.4)和(5.5)可知,迭代加权最小二乘法所得的序列极限β(∗)是最小化问题(4.1)的最优解.证毕!
6.调节参数的选取
调节参数λ的选取对算法的表现十分重要,其常用的选择方法有交叉验证(cross-validation),AIC (Akaike information criterion)[17]和BIC (Bayesian information criterion)[18]等等.本文,我们采用BIC准则来选取调节参数λ.
给定调节参数λ,记迭代加权最小二乘法收敛所得β的最优估计为
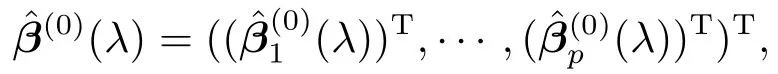
众所周知,回归模型可能存在将非零系数估计为零,或者将零系数估计为非零的可能.为此,我们需要选定一个合适的容许误差,记为tols.若对某个1≤k ≤8,有(λ)(1≤j ≤p)≥tols,其相应的位点j将被纳入活动集(active set)Â(0)(λ)中.否则,该位点将被纳入非活动集(non-active set)((λ))C中,并将其对应的效应值压缩为零.
为了选取最优调节参数λ,我们需要针对其不同的可能取值,采用迭代加权最小二乘法.实际运算中,我们将log(λmax)至log(λmin)等分得到从大到小排列的N个取值,并记为λ=(λ1,··· ,λN),然后按照下述步骤确定最优调节参数.
步1 令i=0,tols=0.001.记此时迭代加权最小二乘法所得的β的最优估计为(λ).
步2 令i=i+1,λ=λi.取(λ)为β的初始估计,通过迭代加权最小二乘法可得β的第i步估计(λ).分别记此时的活动集和非活动集为(λ)和((λ))C,可按下式计算得BIC的值.
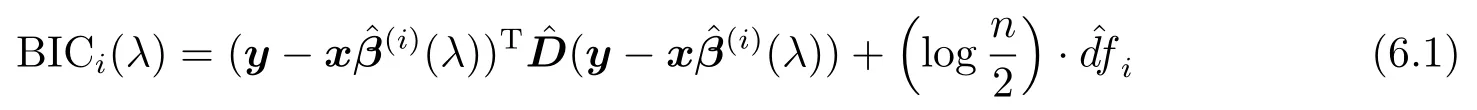
步3 当i ≤N时,返回步2.否则,转向步4.
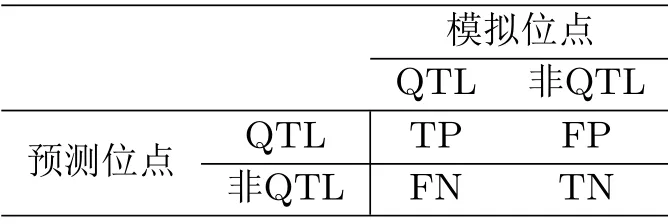
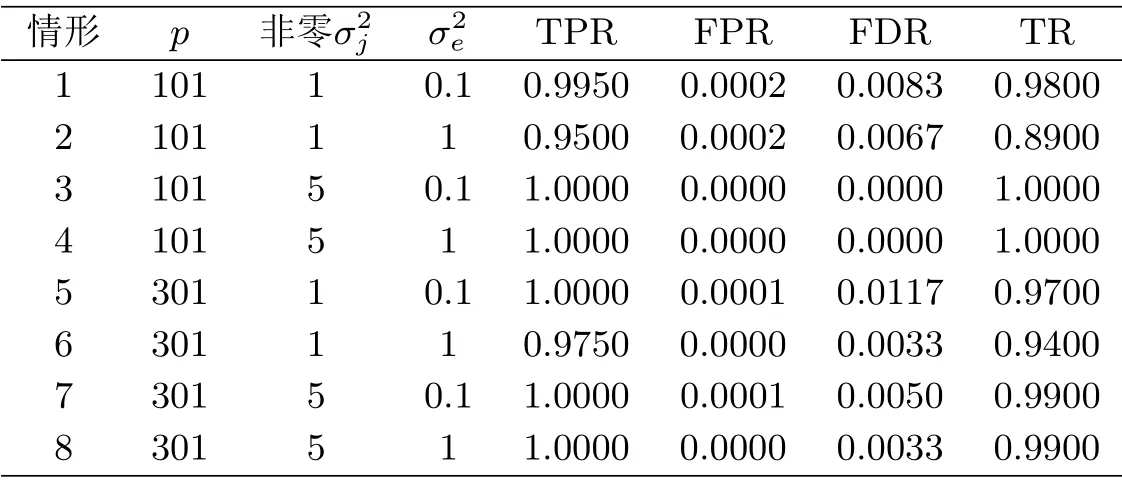
步4 使得由式(6.1)计算所得的BIC值最小的对应λ,不妨记为λs,即为最优的调节参数.与之对应的活动集={i1,··· ,iS},1≤i1<··· 为了评价本文所提方法的优劣,我们进行了模拟计算.这里,我们假定CC-RI父系共有L= 100个.按照ZOU等[4]所提的循环(loop)实验设计,将所有的L个CC-RI排成环形,然后每个CC-RI均与接下来的J= 3的CC-RI品系杂交,从而可产生n= 300个CC-RIX样本.进一步,假定有p=101和p=301个位点等间距分布在染色体上,其中有2个等间隔分布的数量性状位点.数量性状位点所对应的主基因效应方差σ2j为1或者5,而非数量性状位点所对应的主基因效应方差为0.主基因效应βj由8维正态分布N(0,σ2jI8)产生.多基因效应方差σ2a设置为0.1,而残差方差σ2e设置为0.1或者1.从而,交叉组合可得8种不同的参数组合设置. 对每一种参数组合,随机产生100个模拟数据集.其中,每个CC-RI品系的单个位点基因均有1/8的概率继承8个祖先中的任何一个,按照RIX循环实验设计,即可得到基因型矩阵xj,以及亲缘信息矩阵A. 对每一种参数组合下的每一个数据集,均采用迭代加权最小二乘法进行数量性状位点定位.为了衡量定位效果,我们将其处理成一个二分类的预测问题.如果某个位点为模拟设置的QTL位点,则该位点标记为P(positive,阳性),否则标记为N(negative,阴性).如果一个QTL位点预测为模拟设置的QTL位点,则称为真阳性(true positive,TP),否则称为假阳性(false positive,FP).如果一个预测非QTL位点,为模型设置的非QTL位点,称之为真阴性(true negative,TN),否则称之为假阴性(false negative,FN).从而可得表(7.1)所示的混淆矩阵. 表7.1 混淆矩阵 基于混淆矩阵,定义真阳性率(True Positive Rate,TPR),假阳性率(False Positive Rate,FPR),假发现率(False Discovery Rate,FDR)如下. 同时,对每一种参数组合下的每一个数据集,若预测的QTL恰好与模拟设置的QTL完全相同,称之为“真实”(truth).综合100次模拟,即100个数据集所得的总的“真实”频率称之为真实率(Truth Rate,TR).显然,TPR以及TP越大越好,而FPR以及FDR越小越好.表(7.2)展示了不同模拟设置下,100次模拟所得的TPR,FPR以及FDR的平均值,以及真实率(TR)情况. 表7.2 不同模拟设置下的模型平均表现 从表(7.2)中,不难发现,无论哪种模拟设置下,本文所提模型和方法的表现都非常不错.例如,当p= 101时,真阳性率都超过0.95,而对应的假阳性率和假发现率却十分接近于0.此外,真实率TR也十分接近于1.这充分表明本文所提模型和方法在进行数量性状位点定位中的有效性.若固定其他参数不变,当非零数量性状位点对应的主基因效应方差增大时,模型的表现会越来越好.因为,此时信号强度增强,模型更容易识别真实的QTL位点.若固定其他参数,当模型的残差方差增大时,模型的表现会有所下滑.如情形1和情形2,当σ2e由0.1增大到1时,相应的TPR从0.995减少到0.95.因为此时噪声比例有所加大,从而模型表现整体变差.这一现象与我们的预期是一致的.整体而言,本文所提模型和方法在数量性状位点识别方面具有较高的真阳性率,以及较低的假阳性率,是一种比较好的定位方法. 本文在文[8]的模型的基础上,忽略亲源效应,考虑了一个仅含主基因效应的数量性状位点定位问题.考虑到研究背景,即CC-RIX品系的数据特点,我们采用了组LASSO方法对模型进行转换,并设计了迭代加权最小二乘法求解模型,克服了设计矩阵容易奇异等计算难题.从模拟所得结果来看,本文所提模型和方法,在CC-RIX品系的基因位点定位中具有较好的表现,能准确识别出真实的数量性状位点,并且具有较高的真阳性率以及较低的假阳性率.同时,相比贝叶斯方法而言,本文所提模型和方法还具有计算量小,计算速度快等特点.当位点个数较多时,能体现出其计算上的显著优势.7.模拟计算
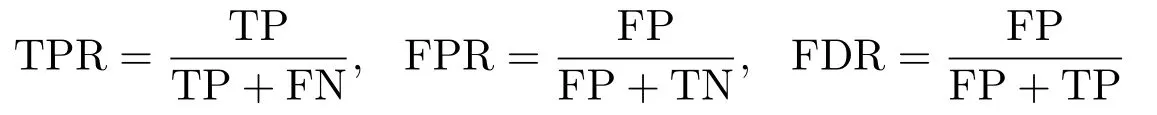
8.结论
