全海深着陆车着底冲击特性与集中应力结构改进

郭 威 孙洪鸣,2 徐高飞 李广伟 周 悦 王敏健,

1.中国科学院深海科学与工程研究所, 三亚, 5720002.中国科学院大学, 北京, 1000493. 上海海洋大学工程学院, 上海, 201306

0 引言

全海深着陆车是为满足深渊海底大范围移动考察、定点位精细作业和强负载作业等需求，将履带式移动底盘与传统水下机器人相结合的一种新型水下机器人[1]。近年来，美国、日本和德国均加紧开展对深海着陆型机器人的研制工作[2]。美国研发的Benthic Rover深海着陆机器人[3]，其潜浮组件仅配有一级压载铁，无法控制其着底时的姿态与速度；德国TRAMPER深海着陆机器人经绞车吊放至海底[4]，对母船依赖较大且操作复杂；德国Wally和VIATOR以及日本的ABISMO均通过光电复合缆与基站进行信息能源交互[5-7]，其复合缆也限制了自身科考范围。本研究中全海深着陆车采用独立自由下潜方式，且配有两级压载铁控制其着底冲击状态，具有潜浮性能好、操作便捷和作业范围广等优点，但由于海底的复杂性和着陆车的自由下潜方式，需对着底姿态及冲击特性进行深入研究。

对着陆冲击响应的研究在航空航天领域较为普遍。FLUGGE等[8]早在1954年就分析了飞机起落架着陆冲击载荷响应，为飞机相关结构的优化设计提供了参考。在飞船返回舱着陆冲击分析方面，马春生等[9]对返回舱着陆速度及姿态进行了讨论，王宇翔等[10]对比分析了飞船返回舱着水和着陆两种情况的响应特性。WU等[11]通过对比太空着陆器自由和低速时的动力学模型，提出基于主机推力的稳定着陆方式，以提高其着陆过程的安全性。洪煌杰等[12]建立了装备-气囊有限元模型，对空投装备着陆时初速度、侧倾角和俯仰角与气囊最大压力的关系进行了研究。在海洋装备领域，胡勇等[13]分别对载人潜水器冲击岩石和软沉积物海底进行了安全性分析，并提出了安全坐底建议。胡永利等[14]针对重载作业型遥控潜水器水下升降装置进行了着底碰撞仿真，对比了5种着底工况的仿真结果，分析了着底速度对碰撞结构动力响应的影响。对于深海着陆型机器人，文献[15-17]都聚焦于海底泥土受力模型和爬行运动性能研究，而对着底过程的运动和冲击响应研究较少。为把握着底冲击过程的一般规律，对可控速度与姿态的着陆车进行着底特性分析并改进显得尤为重要。

本文针对正在研制的全海深着陆车原理样机，阐述其下潜着底组件的工作原理，分析着陆车着底过程运动规律，对其不同速度与角度的着底冲击进行数值模拟，进而对关键部件进行改进设计，以确保着陆车平稳着底，提高设备安全性。

1 下潜与着底过程

全海深着陆车下潜着底过程受底盘前部一级压载、后部二级压载以及重心和浮心连成的轴线位置的应急推进器控制。在目标作业海域，着陆车经母船吊放装置布放至海面，脱离母船后在两级压载铁的作用下以无动力的方式开始下潜，在距海底一定高度时抛弃一级压载铁，同时其姿态调整为水平并降低速度完成着底。着陆车自由下潜过程如图1所示。

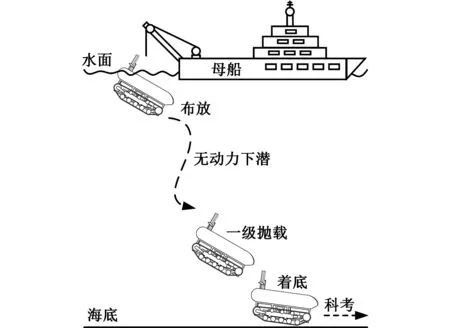
图1 着陆车自由下潜过程Fig.1 The free diving process of state of landing vehicle

图2所示为着陆车一级抛载前状态，其重心CG与浮心CB垂向轴线相距l，稳心高度h；图3所示为着陆车一级抛载后状态，其重心CG与浮心CB位于同一垂向轴线；结束海底科考任务后抛弃二级压载铁，着陆车艉部翘起并实现离底上浮。在着底和离底过程中，推进器将作为应急装置，为着陆车提供着底和助力上浮的保障。

图2 着陆车一级抛载前状态Fig.2 State of landing vehicle before first ballast unloading

图3 着陆车一级抛载后状态Fig.3 State of landing vehicle after first ballast unloading

采用文献[1]的优化设计结果：一级压载铁距中轴线距离xa为0.38 m，质量ma为53 kg；二级压载铁距中轴线距离xb为0.58 m，质量mb为50 kg；着陆车其他主要技术参数如表1所示。

2 着底模型分析

在着陆车结构设计中，对整体结构和安装布局作了对称设计，且留有安装空间，可完成整体对

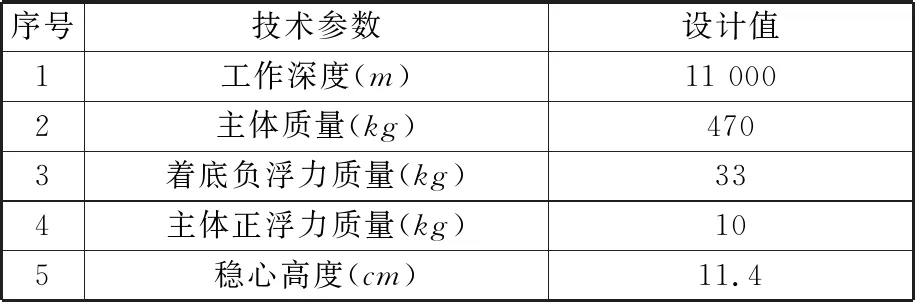
表1 主要技术参数Tab.1 Main technical parameters

称微调，因此其着底过程为相对大地坐标系EXYZ在EXZ平面的直线运动和相对运动坐标系exyz绕y轴的旋转运动。着陆车着底过程平衡状态主要包括一级抛载前的初平衡和一级抛载后的再平衡，着底过程受力分析如图4所示，在EXZ平面内着陆车受竖直方向的负浮力F、相反于运动方向的阻力D、垂直于运动方向的升力L及绕y轴的纵倾力矩My共同作用下完成稳定下潜着底。

图4 着底过程受力分析Fig.4 Stress analysis during landing

着陆车着底过程中的两种平衡状态应满足以下函数关系：

L1,2sinα1,2+F1,2sinθ1,2-D1,2cosα1,2=0

(1)

L1,2cosα1,2+D1,2sinα1,2-F1,2cosθ1,2=0

(2)

(m+ma+mb)g(hsinθ1,2-lcosθ1,2)=My1,2

(3)

F1,2=(ma0+mb0+m0)g

(4)

l=xama/(m+ma+mb)

(5)

ma0=ma-ρhma/ρs

(6)

mb0=mb-ρhmb/ρs

(7)

式中，L1,2、D1,2、My1,2分别为着陆平衡状态的升力、阻力和纵倾力矩；α为攻角；θ为纵倾角；m为主体质量；m0为主体正浮力质量；ma0为一级压载铁负浮力质量；mb0为二级压载铁负浮力质量；ρh为所处深度海水密度，ρs为压载铁密度,ρs=7800 kg/m3；同一物理量的下标1和2分别表示初平衡状态和再平衡状态。

由文献[18]的水动力分析法可知，着陆车平衡状态阻力D1,2、升力L1,2和纵倾力矩My1,2的方程分别为

(8)

(9)

(10)

式中，V为着陆过程潜航速度；KD0、KD、KL0、KL、KM0、KM为着陆车模型参数，根据文献[1]，KD0=405.8，KD=402.4，KL0=598.2，KL=-130.8，KM0=267.5，KM=-40.9。

基于着陆车着底过程平衡状态分析，将式(4)～式(10)代入式(1)～式(3)整理得到:

[(m+ma+mb)ρshcosα1,2-maxaρssinα1,2]AD- [(m+ma+mb)ρshsinα1,2+maxaρscosα1,2]AL-

[(ma+mb)(ρs-ρh)-ρsm0](KM0+KMα1,2)=0

(11)

(12)

(13)

AD=KD0+KDα1,2AL=KL0+KLα1,2

由式(11)～式(13)可获得着陆车初平衡状态和再平衡状态时纵倾角θ、航迹角β及潜航速度V的大小。

为分析着陆车初平衡和再平衡状态所处不同深度时，其水密度变化对状态参数值的影响，将讨论下潜至8000 m和11 000 m各状态参数变化量的大小。由文献[19]蛟龙号5000 m海试所获数据经光顺处理后可知海水密度ρh随深度H的线性变化关系，并可将其关系近似为ρh=0.005H+1025，计算得不同深度平衡状态纵倾角θ1,2、航迹角β1,2及航速V1,2大小及变化量，如表2所示。

由表2可知，在距海底一定范围内，不同深度的海水密度对平衡状态参数大小的影响可忽略不计，因此本文着陆车初平衡和再平衡状态各参数取为11 000 m海水密度计算所得数值。

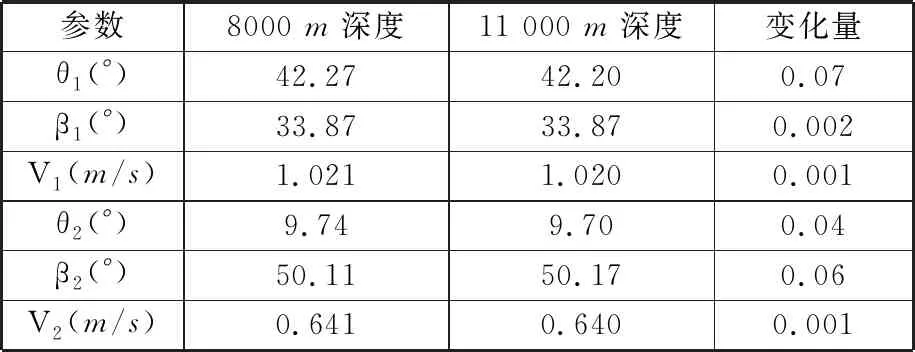
表2 不同下潜深度平衡状态参数Tab.2 Parameters of balanced state for differentdepths of diving

3 冲击特性分析

由以上分析可知，着陆车理想着底过程包括：初平衡状态、调整状态和再平衡状态三个阶段，且在距海底一定高度时抛弃一级压载铁开始着底。但鉴于海试过程着底时机的不确定性，将初平衡状态作为拟着底状态1，再平衡状态作为拟着底状态6，利用插值法将两边界状态参数处理成6个拟着底状态，并分别对其进行冲击响应分析，各拟着底状态参数如表3所示。

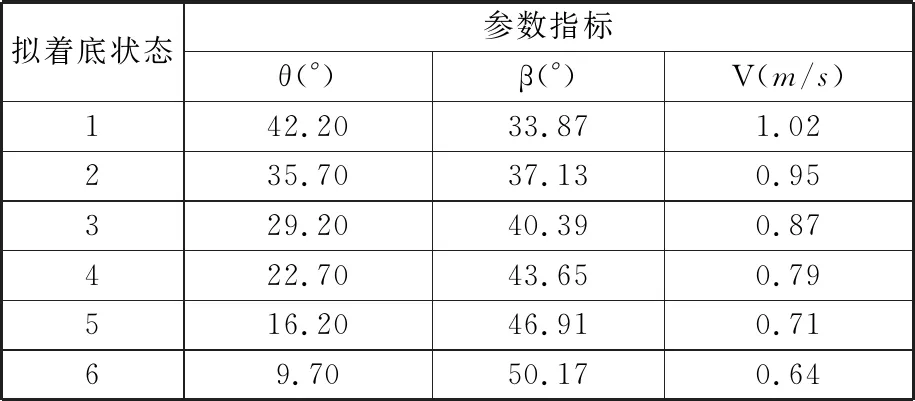
表3 拟着底状态参数Tab.3 Parameters of imitated landing state

3.1 碰撞理论

着底冲击是一个动态、复杂的碰撞过程，系统除了具有结构和材料的非线性以外，还有接触界面的非线性，通常采用显式积分算法对着陆车着底冲击的瞬态动力学过程进行数值模拟分析[20]。

在总体坐标系下，着陆车碰撞方程表示为

Ma+Cv+Kd=Fex

式中,M为结构质量矩阵；C为结构的阻尼矩阵；K为结构的刚度矩阵；a为加速度向量；v为速度向量；d为位移向量；Fex为包括碰撞力在内的外力向量。

内部力向量

Fin=Cv+Kd

(15)

惯性力向量

Fre=Fex-Fin

(16)

碰撞方程可写为

Ma=Fre

(17)

若碰撞结构采用集中质量，即质量矩阵M为对角矩阵，则各自由度方程将相互独立为

(18)

采用中心差分的显式格式对式(18)进行时间积分可得速度vi，再积分可得位移di。在总体坐标系下，碰撞运动方程可表示为

vn+1/2=vn-1/2+an(Δtn+1/2+Δtn-1/2)/2

(19)

dn+1=dn+vn+1/2·Δtn+1/2

(20)

Δtn+1/2=(Δtn+Δtn+1)/2

整个时域范围内，由式(19)、式(20)可求得各离散时间点处的速度和位移，显式积分法不需要矩阵分解或求逆，也不存在收敛性问题，因此可利用显式有限元法对着陆车冲击模型进行数值模拟分析。

3.2 有限元建模

建立合理有限元模型是数值模拟的前提。考虑到着陆车自身结构非线性和着底环境多变性，在建模过程中对冲击模型进行适当简化：①忽略着陆车内部部件结构特征，重点分析主框架冲击响应特性；②忽略着底点海底地面多变性，选择以普通平板地面为冲击目标。

首先利用SolidWorks软件建立着陆车着底模型，简化并删去与着底冲击无关的特征，着陆车着底简化模型如图5所示，包括浮力材、主框架、履带和海底，然后利用Workbench LS-DYNA进行数值求解。

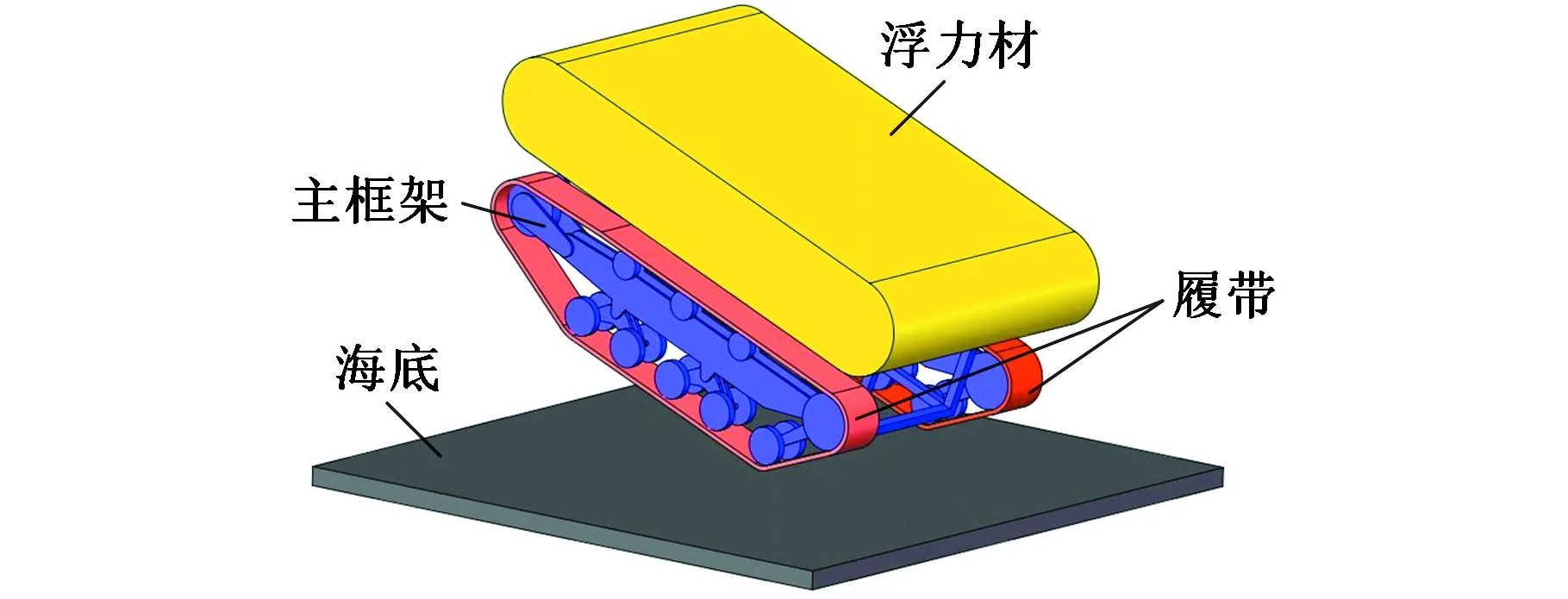
图5 着陆车着底简化模型Fig.5 Simplified model of lading vehicle

为保证计算结果精度，缩短数值求解时间，对碰撞区域结构的网格进行加密，履带和主框架网格单元尺寸大小分别为0.01 m和0.015 m，其他两部分网格单元尺寸皆为0.04 m。着陆车有限元模型如图6所示，其整体网格节点数为82 654，单元数为136 205，网格正交质量为0.76，扭曲度为0.25，总体网格质量评价为优[20]。

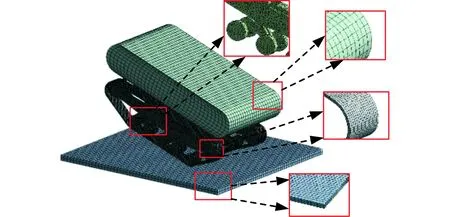
图6 着陆车有限元模型Fig.6 Finite element model of landing vehicle

由于建模过程中对实际结构进行简化，且着陆车水下负浮力质量与空气质量相差较多，为保证着陆车实际重心位置和水中负浮力质量保持不变，其浮力材、主框架和履带各材料密度应以质量反算所得等效密度表示，其材料主要参数如表4所示。

表4 材料主要参数Tab.4 Main parameters of materials

3.3 冲击响应

为描述着底冲击过程的能量转化，把握着陆车应力分布规律，分析车体结构可靠性，以便进行改进设计，考虑着底点存在岩石地面和泥质地面等情况，本节仅分析冲击破坏性大的岩石地面。首先将岩石地面等效为刚性本构模型，并添加刚性约束；其次赋予各结构如表4所示的材料属性，然后对分析模型施加重力场效应以模拟着底环境，同时将着陆车内部各结构间设置为固连接触，履带与海底间为摩擦接触，其摩擦因数为0.2；最后冲击时间和分析步分别设置为0.03 s和40个等空间分布点。

着底冲击能量转化过程任选纵倾角θ为22.7°、航迹角β为43.64°以及潜航速度V为0.79 m/s(拟着陆状态4)作为状态指标，其冲击能量E随时间t的变化关系如图7所示，冲击等效应力分布见图8。

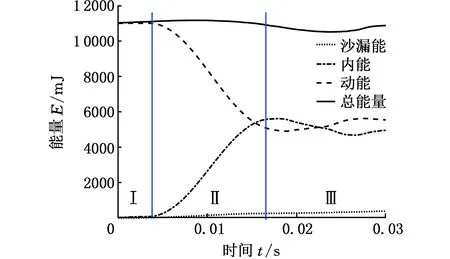
图7 冲击能量-时间关系曲线Fig.7 Relationship between impacting energy and time

图8 碰撞过程应力云图Fig.8 Stress distribution during the impacting

着底冲击过程中，能量随冲击时间以不同形式存在，主要包括动能、内能和沙漏能。如图7所示，区域Ⅰ为着底潜航阶段，其总能量以动能形式存在；区域Ⅱ为着底冲击阶段，着陆车艏部接触海底，其动能从0.004 s开始迅速转化为内能和沙漏能；区域Ⅲ为着底调整阶段，各能量在0.017 s之后趋于稳定，其能量的微弱波动，表征着陆车艉部姿态调整的能量转换。整个过程中，三种主要能量转换无异常波动，且符合能量守恒定律，同时沙漏能所占总能量的比例不超过5%，符合工程实际经验[21]，计算结果不失真。

由于着陆车着底姿态主要受两级压载控制，可设计着底冲击过程基本为正纵倾角的姿态，保证张紧轮位置为初始接地点，其冲击产生的能量经履带直接传递到张紧轮及其支架上，并向着陆车艉部扩散，因此离张紧轮越远，传递到的应力就越小。由图8可见，在能量传递过程中，由于冲击姿态和张紧轮位置，在张紧轮支架处产生了应力集中，且张紧轮支架与履带轮架间的刚性连接结构易产生冲击破坏，需对此敏感部位进行改进设计并分析其效果。

4 改进与分析

由着陆车着底冲击特性分析可见，着底冲击应力集中在张紧轮支架处，且当张紧轮支架与履带轮支架为刚性连接时易产生破坏，这势必严重危害整个着陆车的安全性，故对此部分结构进行改进设计，并结合海底岩石地面和泥质地面等情况分别对其改进前后冲击应力进行数值模拟分析。

4.1 改进设计

将张紧轮支架处的刚性连结改进为以轴承为中间体的铰接，并安装弹簧阻尼器以消除应力集中，且低速轻载的深海着陆车主要承重部件为支重轮，张紧轮改进不会引起较大的波动，图9为张紧轮结构改进前后的示意图。

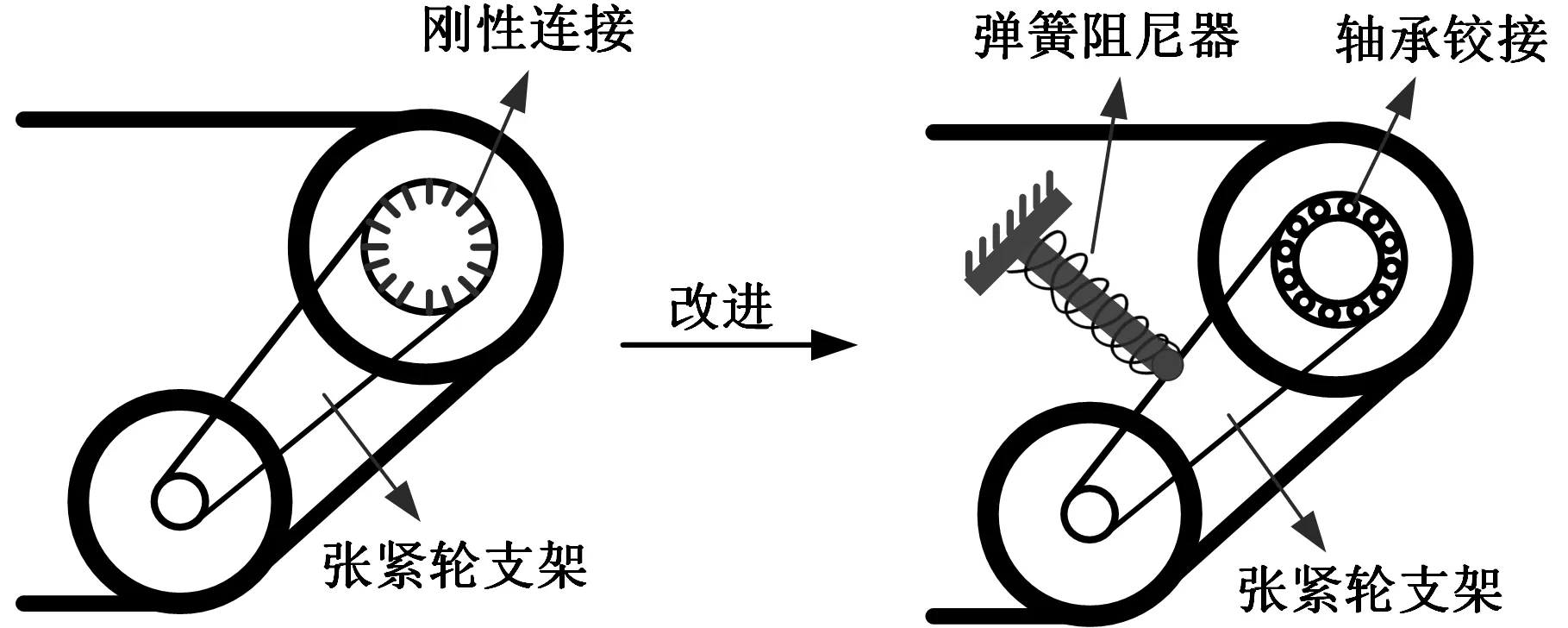
图9 张紧轮改进结构Fig.9 Improved structure of tension wheel

将张紧轮支架与履带轮架之间的固连接触改为摩擦接触，并设摩擦因数为0.2，选取5种刚度系数K分别为80，120，160，200，240 N/mm的弹簧阻尼器，阻尼系数均设置为10 N·s/mm，以研究不同刚度的弹簧阻尼器对着底冲击响应的影响。

4.2 数值模拟分析

岩石地面着底最易对着陆车造成破坏，首先分析刚性本构的硬质地面冲击响应。为分析张紧轮支架改进前后着底冲击变化，研究弹簧阻尼器刚度系数对其的影响规律，实验将针对6种拟着底状态，分别对改进前的刚性连接与改进后5种刚度弹簧阻尼器的铰接共6种冲击结构进行数值模拟[21]。着陆车冲击岩石地面接触点处等效应力-时间关系如图10所示。

由图10所示张紧轮支架改进前后冲击响应与不同刚度弹簧阻尼结构的等效应力-时间关系曲线可得：①改进前的着陆车最大等效应力出现在拟着底状态3，其峰值约为95 MPa；②在冲击岩石地面时，改进后张紧轮支架具有明显缓冲作用，其最大等效应力约为改进前的13%；③弹簧阻尼器刚度系数对冲击应力无明显影响，可结合工程需求选择合适刚度。

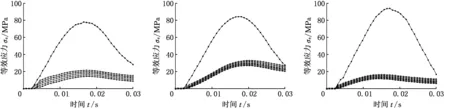
(a)拟着底状态1 (b)拟着底状态2 (c)拟着底状态3

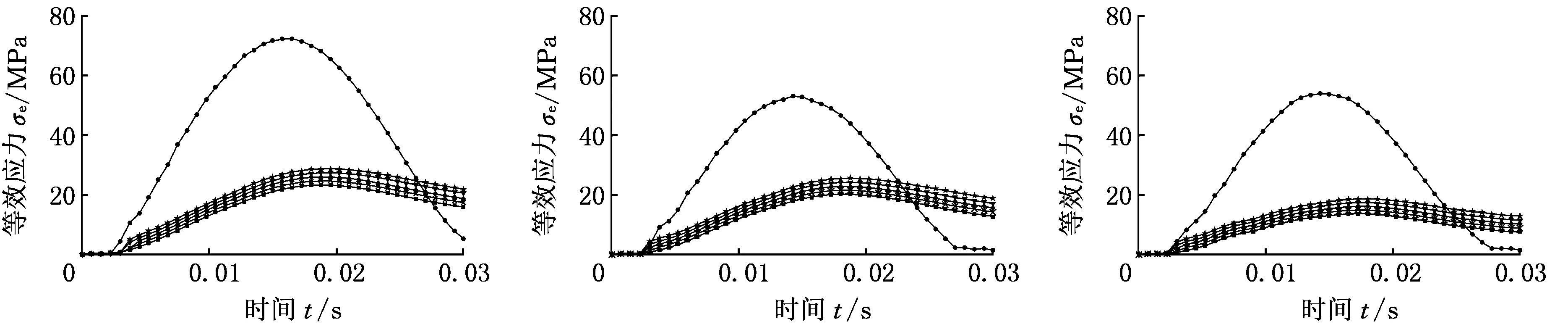
(d)拟着底状态4 (e)拟着底状态5 (f)拟着底状态6 图10 冲击岩石地面等效应力-时间关系曲线Fig.10 Relationship between equivalent stress and time during colliding rock ground

因海底大部区域为泥质地面，为充分掌握各着底状态冲击特性，设计冲击泥质地面仿真实验，并对泥质地面的材料本构模型进行近似处理。根据文献[22]的研究，将泥质海床近似处理为弹塑性模型，且取泥质海底等效参数如表5所示。

结合泥质地面弹塑性本构模型参数，针对6种拟着底状态，分别对其改进前的刚性连接和改进后5种刚度弹簧阻尼器的铰接等6种冲击结构进行数值模拟。着陆车冲击泥质地面接触点处等效应力-时间关系如图11所示。

表5 泥质海底参数Tab.5 Parameters of muddy ground

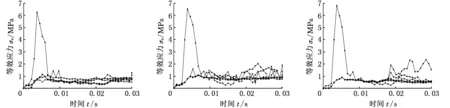
(a)拟着底状态1 (b)拟着底状态2 (c)拟着底状态3

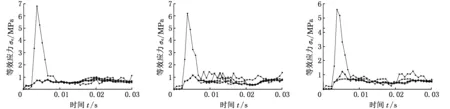
(d)拟着底状态4 (e)拟着底状态5 (f)拟着底状态6

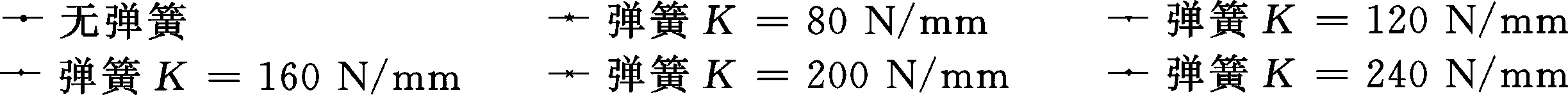
图11 冲击泥质地面等效应力-时间关系曲线Fig.11 Relationship between equivalent stress and time during colliding muddy ground

由图11所示张紧轮支架改进前后冲击响应与不同刚度弹簧阻尼结构的等效应力-时间曲线可得：①在冲击泥质地面时，改进后张紧轮支架具有明显缓冲作用，其最大等效应力约为改进前的30%，且刚度系数对冲击应力无明显影响；②在张紧轮支架改进前，着陆车冲击泥质地面的应力峰值明显减小，约为岩石地面的7%；

③在张紧轮支架改进后，着陆车冲击泥质地面的应力峰值明显减小，约为岩石地面的5%。

5 结论

(1)着陆车着底过程包括一级抛载前的初平衡和一级抛载后的再平衡两个边界状态，且其平衡状态参数受着底过程深度变化的影响可以忽略。

(2)着底冲击过程中，着陆车张紧轮支架处产生了应力集中现象，它与履带轮架的刚性连接结构易发生冲击破坏，应对其结构进行改进设计。

(3)张紧轮支架改进前和改进后，其冲击泥质地面最大等效应力远远小于冲击岩石地面的最大等效应力。且张紧轮支架改进后着陆车最大等效应力大大减小，有效地消除了应力集中现象，提高了车体着底过程的安全性。

本文的研究方法为解决复杂动力冲击过程提供参考，其结果也为其他同类潜水器的研制提供理论依据。研究中忽略了深海复杂环境对着底过程着陆车应力集中点的影响，后续研究需建立深海复杂海流干扰下更为精确的着陆速度和姿态的运动模型，增加弹簧阻尼装置后的稳定性将通过多体动力学软件对不同底盘参数和底质地面进行仿真分析，以获取着陆车质心的滑转率、侧移量和稳定性等方面的影响关系，进一步完善着着陆车的总体优化设计。