基于脉冲漏磁暂态特征的缺陷量化评估方法

许 鹏 方 舟 王 平 耿 明 许 勇

1. 南京航空航天大学自动化学院，南京，211106 2. 工业和信息化部高速载运设施的无损检测和监控技术重点实验室，南京，211106 3. 中铁第四勘察设计院集团有限公司，武汉，430063

0 引言

我国铁路高速、高载和行车密度大，轨道安全问题日益突出。为了保障铁路运行的安全，需对钢轨缺陷进行长期、及时、高效的检测与评估，而无损检测技术具有非破坏性、包容性和动态性等特点，对钢轨缺陷的检测与评估有着至关重要的作用。目前，无损检测技术已经从无损探伤(NDI)阶段发展到无损检测(NDT)阶段，并逐步向无损评估(NDE)阶段进行过渡，人们不仅希望能够准确地对钢轨缺陷进行识别，而且希望能对裂纹参数进行定量评估, 从而对钢轨的运行状态进行有效监测, 对损伤钢轨进行相应的维护。 目前常见的钢轨无损检测方法有超声检测、涡流检测、磁粉检测和漏磁检测等。超声检测是利用超声波对金属构件内部缺陷进行检查的一种无损检测方法,其穿透能力较强，能够清晰有效地识别钢轨的缺陷细节[1]，并对缺陷的纵向长度、倾角、深度等参数进行评估[2]，但存在需要耦合剂、直观性差以及对近表面缺陷不敏感等缺点。涡流检测[3]是一种基于法拉第电磁感应定律的电磁检测方法，具有不需要耦合剂、检测速度快的优点，但是只适用于金属导体浅表面缺陷的检测。磁粉检测以磁粉做显示介质对缺陷进行观察，其检测结果直观，检测成本较低，但需要磁悬液，目前磁粉已逐渐被磁敏传感器所取代。相比于磁粉检测，漏磁检测精度高、速度快，操作简便且无需耦合剂，在铁轨、管道、钢材等的缺陷检测中得到了广泛的应用。高运来等[4]、ANTIPOV等[5]通过漏磁检测对钢轨缺陷进行了量化评估。

脉冲漏磁(pulsed magnetic flux leakage，PMFL)检测结合了涡流检测和漏磁检测技术的优点，采用脉冲信号作为激励信号。经过傅里叶变换，脉冲信号可以分解为基波和一系列谐波信号之和，其中,低频成分适用于检测深层缺陷而高频成分适用于检测表面和近表面缺陷，因此脉冲漏磁检测可以获得丰富的缺陷信息[6]。目前，对缺陷的定量评估大多是对表面开口缺陷的宽度、深度和角度等参数进行评估[7]，很少有针对埋藏缺陷的评估方法，尤其是对埋藏深度(内部缺陷上表面到试件上表面的距离)和缺陷深度同时量化评估的研究更是接近空白，然而在实际的铁路运营中，钢轨缺陷包括滚动接触疲劳裂纹、内部缺陷、压溃、侧磨、剥离等多种类型[8-9]，其中轨头核伤会导致钢轨发生突然脆断，是最危险的钢轨疲劳缺陷之一[10]。核伤起源于轨头内部由于制造缺陷产生的细小裂纹，在列车运行荷载的反复作用下，这些细小裂纹先是成核，然后向轨头四周逐渐扩大形成疲劳裂纹。对轨道表面和近表面伤损同时进行检测和定量评估，对铁路的安全运行有着重要意义。

徐中行等[11]、许鹏等[12]发现，由于存在涡流效应，激励电压和磁芯磁导率较小时，脉冲漏磁检测信号存在过冲现象，并根据有过冲时的检测信号对缺陷参数进行了定量评估。唐莺等[13]也发现了类似的过冲现象。然而，为了得到较大的检测信号，往往向激励线圈施加较大的激励信号，此时漏磁信号不会出现上述过冲现象[7,14-18]，因此，有必要寻找无过冲信号的新的特征量来对缺陷参数进行量化评估。一些学者研究发现，部分没有过冲的漏磁信号在上升沿会出现上升速率减缓的波动现象[11,14-15,17]。本文基于脉冲漏磁检测中漏磁信号没有过冲的情况，同时对缺陷的深度和埋藏深度进行评估:使用ANSYS Maxwell软件对脉冲漏磁检测模型进行有限元建模与仿真，并根据仿真结果分析波动产生的原因;从脉冲漏磁信号的一阶导数信号中提取两个暂态特征量，并建立特征值与缺陷参数之间的函数关系，进而据此对表面和近表面缺陷进行定量评估;最后，用其他轨道缺陷样本对该评估方法的准确性和可行性进行验证。

1 脉冲漏磁检测原理

脉冲漏磁检测原理如图1所示，探头主要由激励线圈、磁芯、被测样本和磁敏传感器组成。在检测时，向激励线圈施加脉冲激励，从而磁化被测样本。当样本没有缺陷时，由于样本的磁导率远远大于空气的磁导率，因此磁力线几乎全部从样本内部通过,当样本表面存在缺陷时，缺陷处的磁导率减小、磁阻增大，导致磁场在缺陷附近发生畸变，部分磁力线从材料表面泄漏形成漏磁场。使用适当的磁敏传感器便可检测到漏磁场，并可将其转化为电压信号输出。

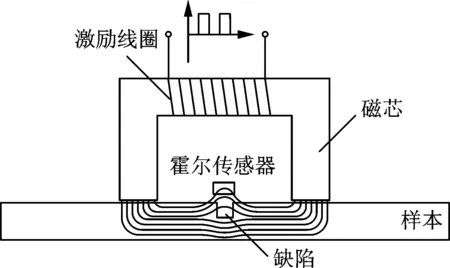
图1 脉冲漏磁检测原理Fig.1 Principle of PMFL detection

据法拉第电磁感应定律，磁通量的变化将产生感应电动势和感应电流，因此当块状导体置于交变磁场或在固定磁场中运动时，导体内将产生闭合的感应电流，即为涡流现象。涡流具有趋肤效应，涡流密度衰减到其表面值的1/e时的透入深度称为趋肤深度，其表达式为

(1)

式中，f为激励频率;μ为磁导率;σ为电导率。

由式(1)可知，趋肤深度随激励频率的增大而减小，因此适当减小激励频率能够提高检测深度，而高频信号更适合于对近表面缺陷的检测。由于脉冲激励包含一系列频率分量，因此它可以在检测远表面缺陷的同时对近表面缺陷保持较高的敏感性。

2 脉冲漏磁检测有限元建模与仿真

2.1 有限元模型

使用ANSYS Maxwell软件建立脉冲漏磁检测的二维瞬态仿真模型如图2所示。该模型由缺陷钢轨、磁芯和励磁线圈组成。钢轨导电率为4×106S/m，铁心材质为铁氧体，相对磁导率为400，导电率为0.01 S/m，绕组采用20 V方波激励，方波周期为1 s，占空比为50%。如图3所示，传感器位于缺陷中心线右侧1 mm，提离为1 mm，检测Y方向的磁场。

图2 脉冲漏磁检测仿真模型Fig.2 PMFL detection simulation model

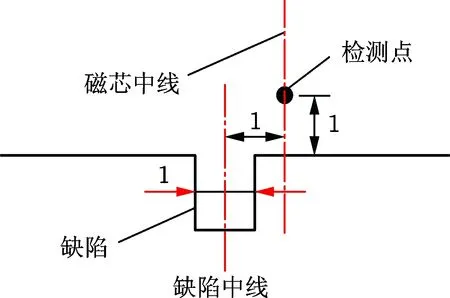
图3 检测位置示意图Fig.3 Detection point diagram

2.2 涡流效应对检测信号的影响

为了分析波动现象产生的原因，对相同的漏磁检测模型进行两次仿真，其中一次考虑涡流效应的影响，结果如图4a所示。可以看出，在约10～40 ms的时间段，实线的上升速度减缓并出现波动，而虚线则未出现该现象。为了放大波动现象，绘制了漏磁信号的一阶导数曲线，如图4b所示。出现波动现象曲线的导数有两个极大值点和一个极小值点，而没有波动的曲线只有一个极大值点，没有极小值点。由此可以说明，是涡流效应引起了曲线的波动现象。

(a)脉冲漏磁信号

(b)脉冲漏磁信号的一阶导数信号图4 是否考虑涡流效应的信号比较Fig.4 Comparison of signals considering eddy current effect or not

当向激励线圈施加激励电压时，电压瞬间增大，此时样本中的磁通量也由零开始快速增大。根据法拉第电磁感应定律，此时样本中会产生涡流而阻碍原磁场的增大，因此涡流效应引起的磁场在内部与原磁场的方向相反。如图5所示，假设施加激励后样本内磁力线方向向右，则由涡流效应产生一个向左的磁场(图中虚线)。由于磁力线是闭合的，虽然在样本内部由涡流效应产生的磁场的方向与原漏磁场方向相反，但是在缺陷正上方两磁场的方向相同，两者进行叠加导致漏磁信号增强，因此会出现过冲和波动现象。当电压稳定后，磁通量不再发生改变，涡流效应逐渐消失，因此后来过冲和波动现象消失，磁感应强度最终趋于稳定。

图5 涡流效应对磁路的影响Fig.5 Effect of eddy current on magnetic circuit

2.3 激励电压和磁芯磁导率对检测信号的影响

(a)脉冲漏磁信号

(b)脉冲漏磁信号的一阶导数信号图6 不同激励电压下的漏磁信号及其导数Fig.6 Magnetic flux leakage signal and its derivative in different excitation voltage

(a)脉冲漏磁信号

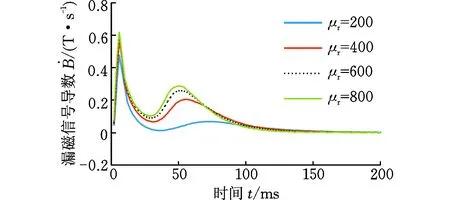
(b)脉冲漏磁信号的一阶导数信号图7 不同磁芯相对磁导率下的漏磁信号及其导数Fig.7 Magnetic flux leakage signal and its derivative in different magnetic core relative permeability

脉冲漏磁检测信号不仅受到涡流效应的影响，还与激励电压以及激励线圈磁芯的磁导率有关。图6和图7所示分别为在不同激励电压(U)和磁芯相对磁导率(μr)下的检测信号及其导数。当激励电压和磁芯磁导率都较小时，原漏磁场较小，涡流效应产生的影响比较明显，因此会产生过冲现象。而当激励电压和磁芯磁导率逐渐增大时，原漏磁场也逐渐增大，涡流效应的影响相对减小，此时过冲现象逐渐消失转变为波动现象。当激励电压和磁芯磁导率足够大时，上升阶段的波动也将变得不明显，凭目测很难观察到。在以往的检测过程中,为了使漏磁信号较大，所加激励也较大，涡流效应的影响不够明显，因此没有发现上述现象。但是这些信号的导数都有两个极大值点和一个极小值点，证明了波动现象的确存在。

2.4 缺陷深度和埋藏深度对漏磁信号的影响

为了对不同缺陷深度和埋藏深度的轨道核伤进行评估，分析了缺陷深度d和埋藏深度b对脉冲漏磁信号的影响。缺陷深度d=6 mm，埋藏深度b变化时的脉冲漏磁信号如图8所示。埋藏深度b=1 mm，深度d为2，3，…，8 mm时的缺陷信号及其导数如图9所示。由图8可知，上表面和近表面缺陷的漏磁信号出现波动现象，而埋藏深度为4 mm及以上的缺陷漏磁信号没有出现波动现象。这是由于涡流具有趋肤效应，波动现象只能发生在表面及近表面的缺陷中。从图9可以看出，深度越小，波动现象越明显。

(a)脉冲漏磁信号

(b)脉冲漏磁信号的一阶导数信号图8 不同埋藏深度缺陷的漏磁信号Fig.8 Signals for defects of different burial depth

(a)脉冲漏磁信号

(b)脉冲漏磁信号的一阶导数信号图9 不同深度缺陷的漏磁信号Fig.9 Signals for defects of different depth

3 基于导数信号的缺陷量化评估方法

3.1 特征提取与缺陷评估

由于缺陷埋藏深度过大时漏磁信号不会出现波动现象，因此可以首先确定波动现象的出现范围。仿真分析深度为2，3，…，8 mm，从上表面以1 mm步长向下移动至下表面的一系列缺陷，如图10所示。可以看出，区域Ⅰ内缺陷的漏磁信号存在波动现象，区域Ⅲ内缺陷的漏磁信号没有出现波动现象。区域Ⅱ中的缺陷由于仿真步长的限制，无法确定是否存在波动现象。受样本厚度的限制，所有缺陷只可能出现在这三个区域内。

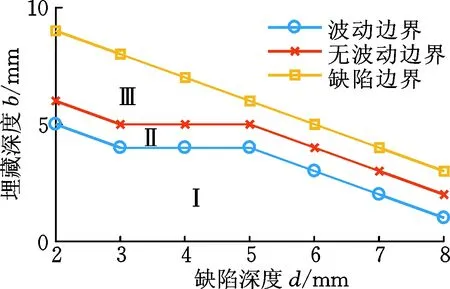
图10 波动现象出现的范围Fig.10 Range of fluctuations

(a)脉冲漏磁信号

(b)脉冲漏磁信号的一阶导数信号图11 极大值时间 t1和极小值时间 t2示意图Fig.11 Diagram of maximum time t1 and minimum time t2

在实际的轨道检测中，需要及时检出轨头核伤并对伤损尺寸、位置进行评估，从而对伤损钢轨进行检修维护，避免裂纹进一步扩展造成严重后果，因此本文研究了波动现象与缺陷深度及埋藏深度间的关系，以此对缺陷进行量化评估。以图11为例，当漏磁信号出现波动现象时，从信号导数中提取两个特征值：第一个极大值的出现时间t1和极小值的出现时间t2，各缺陷的t1和t2如图12所示。从图12中可见，在一定误差范围内，t1与埋藏深度近似成线性关系，与缺陷深度无关；t2与缺陷深度近似成线性关系，与埋藏深度无关。基于此线性关系，即可利用极值时间t1、t2对缺陷深度及埋藏深度进行量化评估，如图13、图14所示。分别用一次函数对b-t1及d-t2进行拟合，拟合函数为

b= 0.2t1-0.04

(2)

d=- 0.2t2+10.1

(3)

(a)缺陷深度 d、埋藏深度 b、极大值时间 t1三维图

(b)缺陷深度 d、埋藏深度 b、极小值时间 t2三维图图12 缺陷参数与极值时间 t1、 t2的关系图Fig.12 Relationship between defect parameters and extremum time t1, t2

图13 埋藏深度 b和极大值时间 t1的拟合曲线Fig.13 Fitting curve of burial depth b and maximum time t1

图14 缺陷深度 d和极小值时间 t2的拟合曲线Fig.14 Fitting curve of defect depth d and minimum time t2

拟合值与真实值的误差如图15所示。分别计算每个缺陷拟合值与真实值的相对误差，其中埋藏深度拟合值与真实值的最大相对误差为10%，缺陷深度拟合值与真实值的最大相对误差为16%。由此可以得到区域Ⅰ内轨道缺陷的量化评估方法：首先，采用脉冲漏磁方法对轨道进行检测；其次，求取检测信号的一阶导数信号，并提取导数信号的两个特征值(第一个极大值时间t1和极小值时间t2)；最后，分别将t1和t2代入式(2)、式(3)，即可同时评估缺陷的深度和埋藏深度。

(a)埋藏深度的拟合误差

(b)缺陷深度的拟合误差图15 埋藏深度和缺陷深度的拟合误差Fig.15 Fitting error of burial depth and defects depth

3.2 方法的可行性分析

图16 用于验证的缺陷参数Fig.16 Parameters of defects for verification

(a)埋藏深度

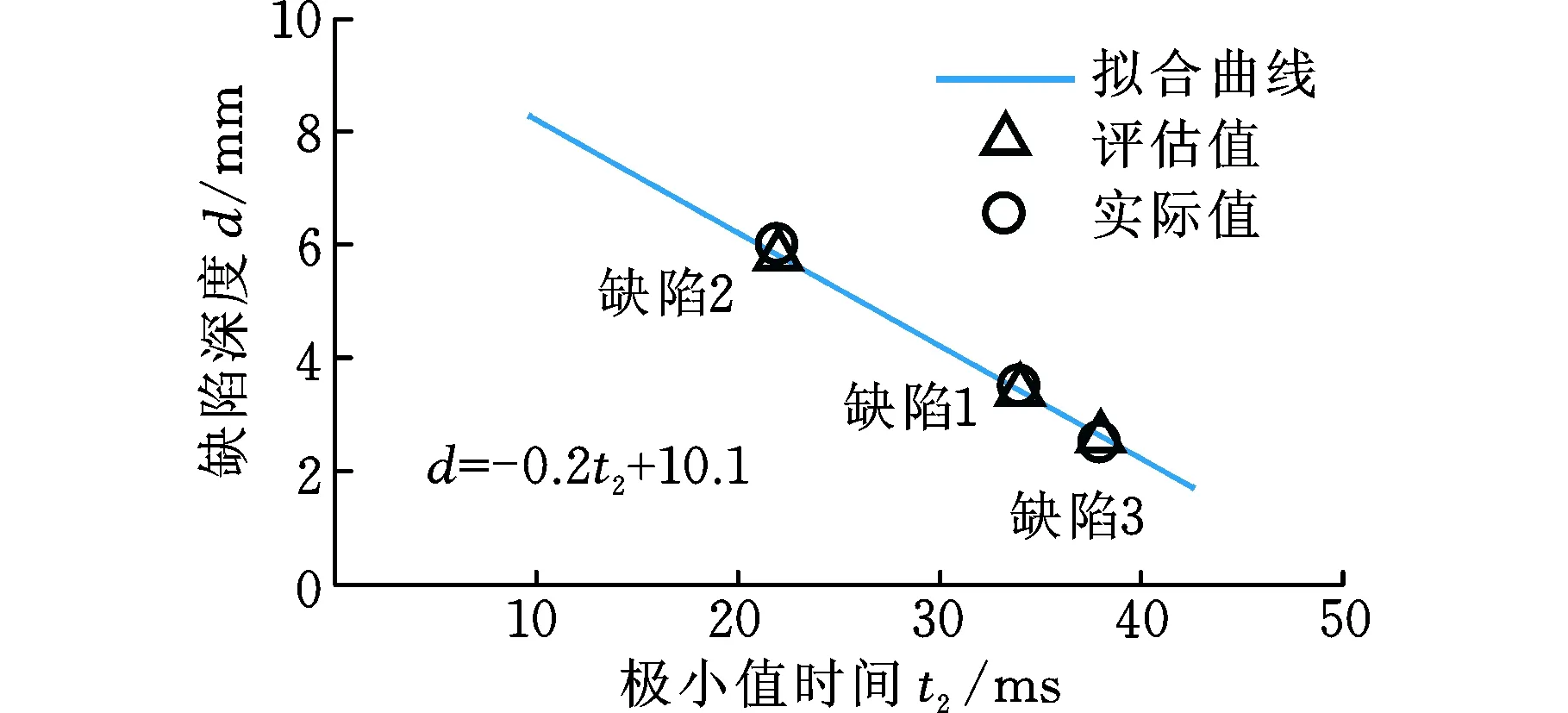
(b)缺陷深度图17 缺陷参数评估值与实际值Fig.17 Evaluation and actual data of defects

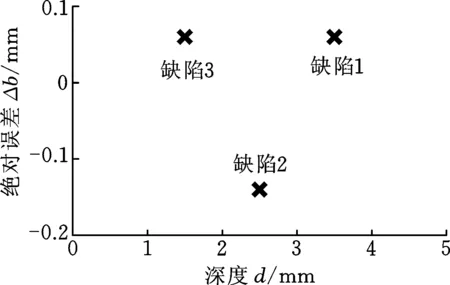
(a)埋藏深度b的误差

(b)缺陷深度d的误差图18 缺陷评估的误差Fig.18 Error of defect quantitative evaluation

为了验证上述方法的可行性，选取了三个新的已知参数的轨道缺陷样本进行评估，如图16所示。分别提取这三个缺陷脉冲漏磁信号导数的极值时间t1、t2，并将其代入式(2)、式(3)，得到对埋藏深度及缺陷深度的评估结果、量化评估值与实际值的误差如图17、图18所示。结果表明，对于该三个样本，本文所述评估方法得到的误差均在0.2 mm以内，满足钢轨缺陷的量化评估要求。

4 结论

本文针对钢轨核伤的无损检测与量化评估问题，提出了一种同时对表面和近表面缺陷的缺陷深度及埋藏深度进行量化评估的方法。研究表明该方法适用于激励信号或磁芯磁导率较大时出现波动现象的脉冲漏磁信号。通过对脉冲漏磁信号的一阶导数信号的分析，从中提取了两个特征值：极大值时间t1和极小值时间t2。分析了特征值与缺陷参数之间的函数关系，并研究了缺陷深度和埋藏深度的量化评估方法。最后，使用三个轨道缺陷的检测信号进行验证，缺陷参数的估计误差均在0.2 mm以内，表明此评估方法是可行的。在之后的工作中，将研究动态检测时基于脉冲漏磁信号特征的缺陷参数评估方法，并从检测信号中提取更多用于评估缺陷参数的特征值。