基于自适应自相关谱峭度图的滚动轴承故障诊断方法

郑近德 王兴龙 潘海洋 童靳于 刘庆运

1.安徽工业大学机械工程学院，马鞍山，2430322.安徽理工大学矿山智能装备与技术安徽省重点实验室，淮南，232001

0 引言

滚动轴承是机械设备中最容易发生故障的零部件。由于滚动轴承在旋转机械中应用广泛，且是关键零件，因此，开展对滚动轴承故障诊断的研究具有重要意义。

故障轴承在运行过程中通常会产生冲击，从而得到一系列非线性、非平稳的振动信号[1]，该振动信号包含着丰富的故障信息，对该信号进行分析和处理，能够达到诊断故障的目的。包络解调分析是最常用的故障诊断方法[2]，其难点是寻找最优解调频带。针对此问题，DWYER[3]提出了谱峭度方法，寻找最大峭度值所对应的频带，并对该频带内信号进行分析得到瞬态成分[4-5]。ANTONI[6-7]提出了快速谱峭度法，分别通过滤波器组结构[6]和短时傅里叶变换[7]计算谱峭度。LEI等[8]提出改进的谱峭度方法，克服了强噪声对快速谱峭度方法的影响，改进谱峭度法利用小波包变换从含噪信号中准确检测到瞬态成分，但是此方法在处理具有强非高斯噪声的振动信号时容易失效。为此，BARSZCZ等[9]提出了Protrugram方法，该方法克服了强非高斯噪声对峭度值的影响，但在此方法中，带宽系数的设置需依据人为经验。针对此问题，WANG等[10]提出了增强的Kurtogram方法，其滤波信号包络谱的峭度可用来显示是否存在故障。上述方法在获取最优解调频带方面取得了较好的成果，但是当故障频率在频谱中不明显或噪声干扰较大时，这些方法会受到限制，从而影响识别解调频带的准确性。

针对上述问题，MOSHREFZADEH等[11]提出了自相关谱峭度图(Autogram)方法，该方法以最大重叠离散小波包变换(maximal overlap discrete wavelet packet transform，MODWPT)为基础，采用二叉树结构对频谱进行分割，从而得到一系列解调频带[12]。Autogram方法通过限制原始信号中的非周期脉冲及噪声来检测周期性脉冲，能够有效抑制非周期分量对实际故障频率的影响，提高检测最佳频带的准确率。然而，Autogram方法在频带分割方面采用二叉树结构，导致计算最佳解调频带时误差相对较大。基于此，本文提出了一种自适应Autogram方法，即利用顺序统计滤波(order statistic filtering，OSF)对信号傅里叶谱进行包络[13-14]，克服了某一频率范围内极大值过于集中的缺点，同时，采用平滑处理，消除了经OSF包络后产生的“平顶”数据。通过寻找包络平滑谱的极大值点，选取距相邻极大值中间位置最近的极小值点作为分割边界，采用经验小波变换(empirical wavelet transform，EWT)对边界内信号进行重构[15-17]，克服原始EWT分割方法的不足[18-19]，同时实现了频谱的自适应分割。

1 自适应自相关谱峭度图

Autogram方法是一种基于无偏自相关检测最佳解调频带的新方法，它能够有效检测到淹没在随机噪声中的解调频带及故障特征频率。该方法以MODWPT为基础进行频带划分[20]，如图1所示，各层带宽固定。通过求取各个频带区域的峭度值，并将值填入到图1中相对应的位置，得到基于Autogram的峭度图。

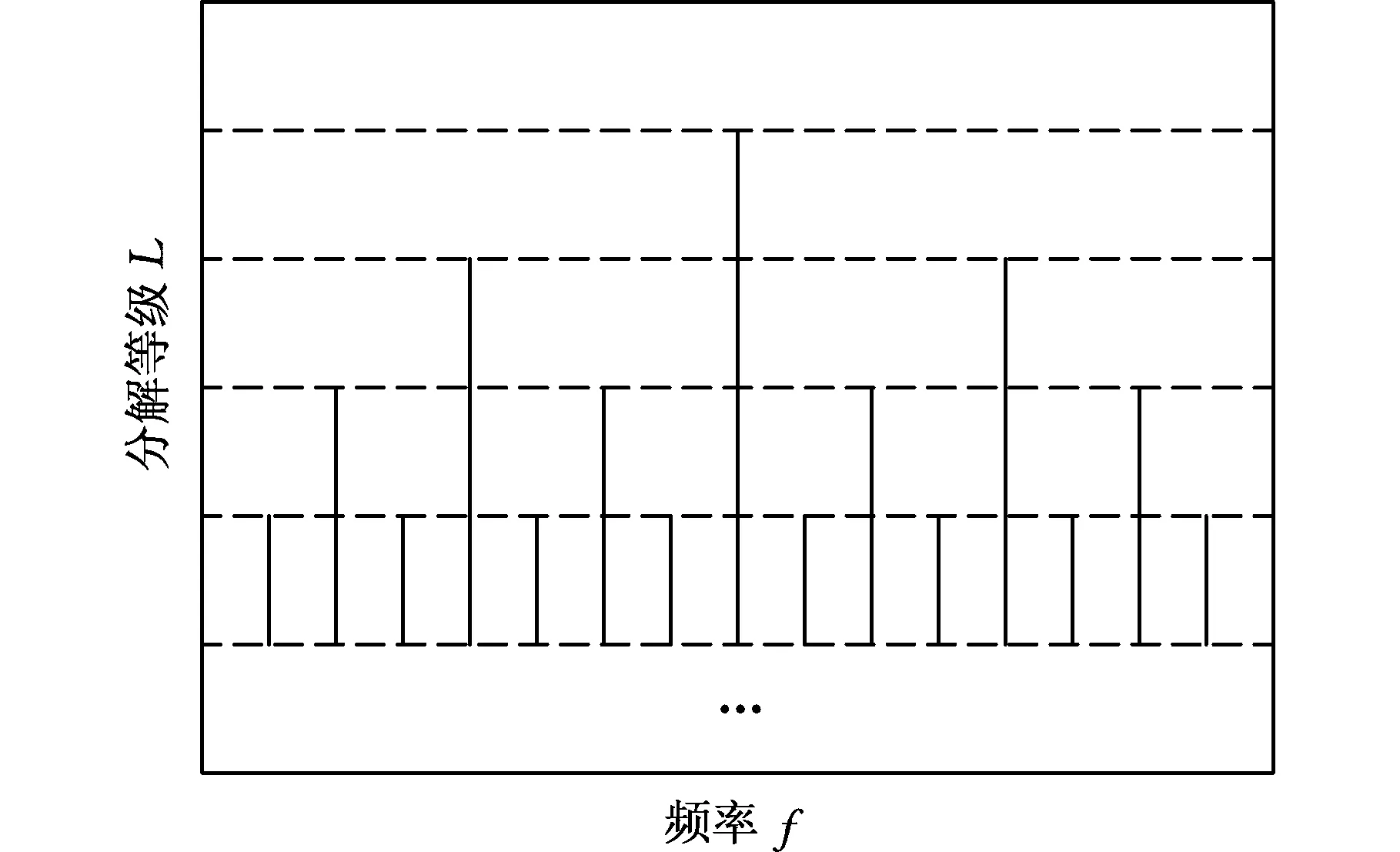
图1 二叉树划分频带Fig.1 Frequency band is divided by binary tree

由于该方法在分割频带时边界位置已经固定，故在划分过程中不能根据信号本身特征自适应确定分割位置。本文采用EWT自适应划分频带，然而EWT中不同的傅里叶谱分割方式对分解结果具有很大的影响。对于含较多干扰成分的信号，传统分割方法得到的结果往往是分割的频带过于集中，影响对其他频率范围内信号的分析，为此，本文以改进的EWT划分频谱。

1.1 基于OSF的改进经验小波变换和频带分割

在划分频带时，可根据原始信号傅里叶谱的具体特征寻找划分边界，以保证冲击明显的分量被包含到所选频带中，避免将最大冲击处直接当作边界的情况出现。具体分割过程如下：①对信号进行傅里叶变换得到其傅里叶谱；②采用OSF对傅里叶谱进行包络，得到包络谱；③采用平滑处理对包络谱进行优化，去除一阶不可微点，避免其对分割结果的影响，从而得到平滑包络谱；④设置分割个数K，寻找平滑包络谱的极大值点与极小值点位置，取所有极大值点的前K个极大值，然后将边界定位到离两相邻极大值中间位置最近的极小值处，此边界即为平滑包络谱的分割位置；⑤将边界进行归一化；⑥选择Meyer小波作为基函数，使用EWT对边界内信号进行重构，完成EWT分解。

OSF包络法本质上是一个具有鲁棒性的非线性滤波器，包括最大值滤波器、中值滤波器和最小值滤波器。与耗时的插值包络不同，OSF耗时较短且能有效去除脉冲噪声。该方法包含一个可变的滑动窗口，通过过滤窗口内的数据，完成对数据的包络。本文以最大值滤波器来估计上包络。

在滤波过程中，首先确定窗口的宽度，然后取窗口内数据的最大值，即

U(n)=max(Wn)

(1)

式中，U(n)为OSF滤波后结果；Wn为第n个窗口内所有数据。

取数组D={2,3,4,5,6,4,8,3,2,1,7}，默认窗口宽度为3。为防止数据长度减小，使用镜像延拓方法，即以原始数据左起第一个数据与右起第一个数据为基点，扩展长度为1，进行镜像延拓。此时数组A变为{3,2,3,4,5,6,4,8,3,2,1,7,1}。根据窗口宽度及式(1)，取{3,2,3}中最大值3，移动窗口，取{2,3,4}中最大值4，{3,4,5}中最大值5，依次类推，得到新的数组{3,4,5,6,6,8,8,8,3,7,7}。具体滤波过程如图2所示。

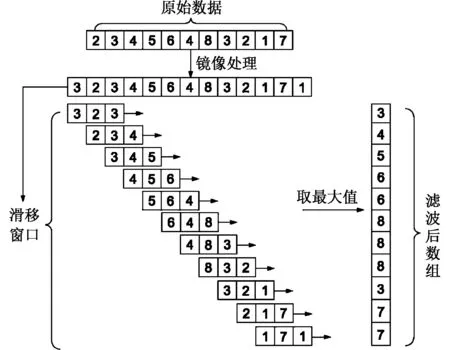
图2 OSF滤波过程Fig.2 Filtering process through OSF

经OSF处理后，包络图中将出现一些“平顶”数据，即为一阶不可微点。为了对此过程进行详细说明，以实测轴承数据包络处理为例，所得结果如图3所示，为了方便观察，选取其中一些“平顶”数据进行标注。

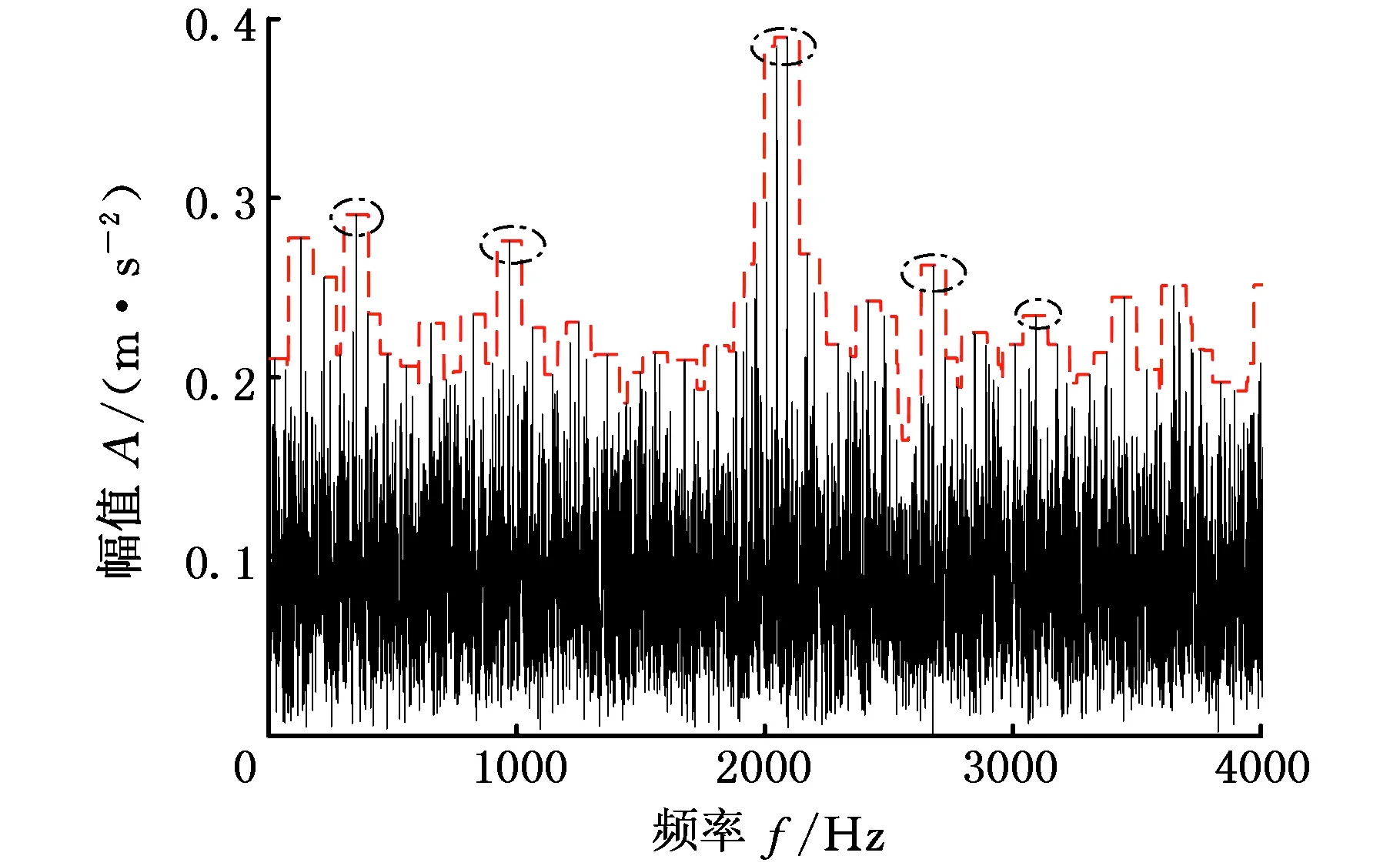
图3 OSF包络处理Fig.3 Envelope processing through OSF

采用平滑处理进一步优化包络数组。本文选取移动平均法进行平滑处理。移动平均法通过将每个数据点替换为跨度内定义的相邻数据点的平均值来平滑数据。此过程等效于低通滤波，即

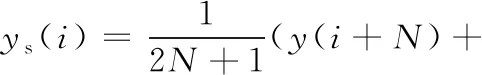
(2)

式中，ys(i)为第i个点的平滑值；N为ys(i)两侧的相邻数据点的数量；2N+1为跨度。

使用移动平均法时需要遵循以下规则：①跨度必须为奇数；②需要平滑的数据点必须在跨度的中心；③对于无法容纳任一侧指定数量相邻的数据点，跨度需要进行调整；④当无法定义跨度时，端点不平滑。

为了进一步说明移动平均法，取跨度值为5进行平滑处理。根据以上规则，前4个元素为

ys(1)=y(1)ys(2)=(y(1)+y(2)+y(3))/3ys(3)=(y(1)+y(2)+y(3)+y(4)+y(5))/5ys(4)=(y(2)+y(3)+y(4)+y(5)+y(6))/5

另外需要注意的是，ys(i)是指排序后的数据顺序，而不一定是原始数据顺序。采用该方法对图3包络数组进行处理，结果如图4所示。由图4可看出，平滑处理有效地去除了一阶不可微点，克服了经OSF包络后无法进一步分割的缺点。

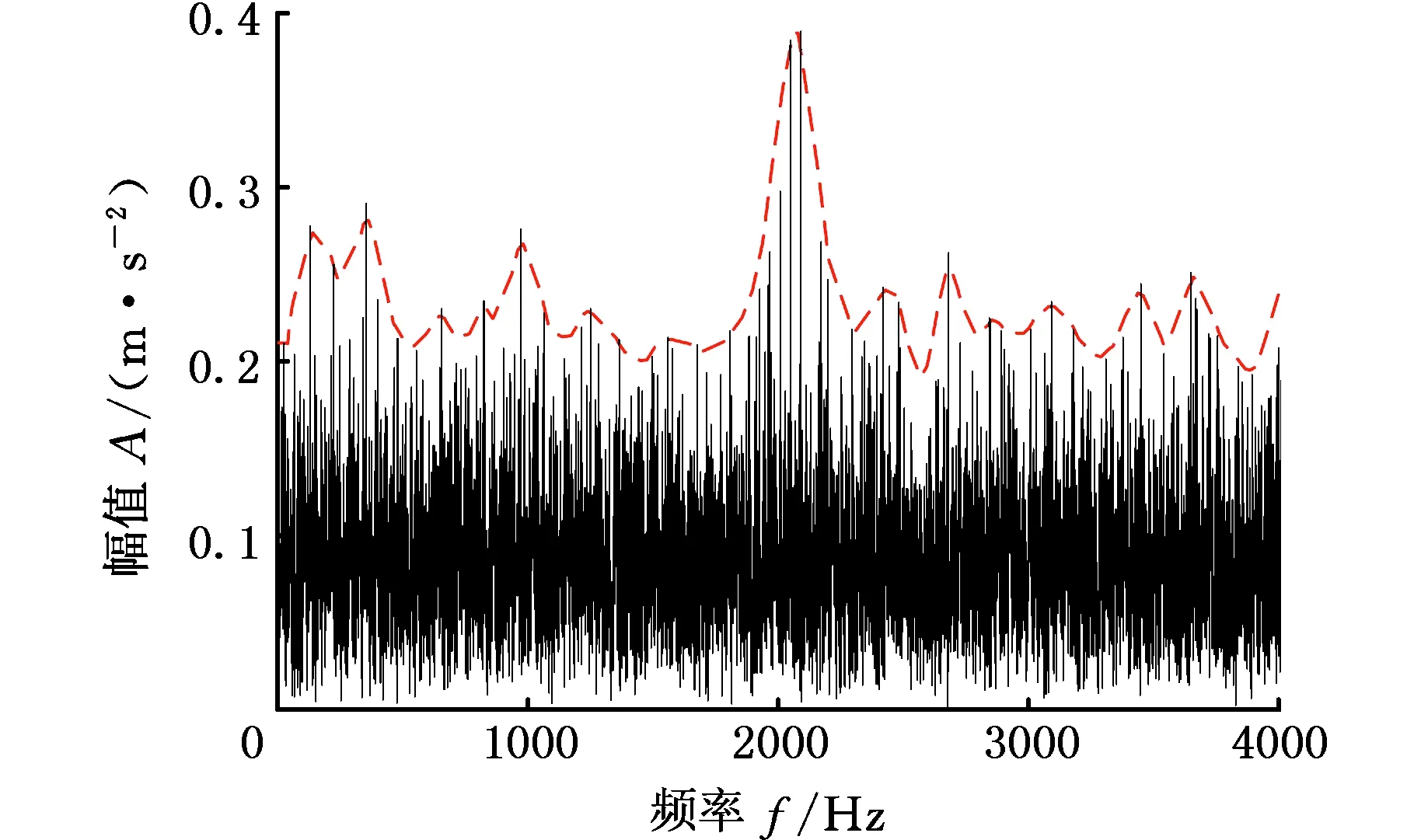
图4 移动平均平滑处理Fig.4 Moving average smoothing

1.2 计算所产生信号的无偏自相关

根据轴承振动信号二阶循环平稳性的自协方差的周期性[21]计算分解信号的无偏自相关，公式如下：

Rxx(ti,τ)=E(x(ti-τ/2)x(ti+τ/2))

(3)

Rxx(ti,τ)=Rxx(ti+T,τ)

(4)

式中，E(·)表示期望值；τ为延迟因子；x为1.1节分解得到的信号。

无偏自相关基于信号平方包络进行计算，即

(5)

τ=q/fs

(6)

式中，X为分解信号的平方包络；M为信号总长度，q=0,1,…，M-1；fs为采样频率。

通过无偏自相关去除信号中不相关的分量(如噪声与无关脉冲)，可提高解调频带内信号的信噪比。经过无偏自相关处理后，噪声在很大程度上会被消除，输出结果更精确。

由式(5)、式(6)可知，随着τ的增大，用于计算无偏自相关的数据样本将减少，导致最终结果的估计方差不足，因此选取无偏自相关结果的前部分进行峭度计算。

1.3 检测最佳解调频带

准确地检测到最佳解调频带是轴承故障诊断的关键步骤。首先计算1.2节中所有包络信号无偏自相关的峭度值，然后寻找最大峭度值对应分量所处的频带，即为最优解调频带。峭度可用来统计数据集峰值，能够检测相关信号的异常脉冲。传统的峭度被定义为

(7)

式中，μx为信号x的均值。

为了量化频带内脉冲信号的脉冲，对传统的峭度方程进行修改，即

(8)

选取所得最大峭度对应的频带，对频带内信号进行进一步分析，绘制其平方包络谱，识别故障特征频率，从而完成对故障的诊断。

2 仿真信号分析

采用周期性冲击仿真信号验证本文方法的有效性，计算公式为

(9)

其中，阻尼系数g=0.03，共振频率fn=12 500 Hz，采样频率为20 kHz。a(t)为周期性冲击信号的基本函数，通过添加信噪比为-12 dB的高斯白噪声，构成特征频率f1为0.1 kHz的仿真信号，其时域波形如图5所示(其中红线为冲击信号)，图6为其傅里叶谱。

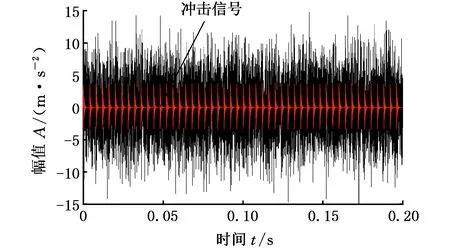
图5 仿真信号时域图Fig.5 Time domain diagram of the simulated signal

图6 仿真信号傅里叶谱Fig.6 Fourier spectrum of simulated signal

首先，采用所提方法对仿真信号进行分析。所得峭度图见图7，图中颜色代表峭度值大小。当分解个数为5时，最大峭度值所处频带的中心频率为4114.5 Hz，带宽为737 Hz。对该频带内信号进行分析，得到其平方包络谱，见图8。由图8可知，所选频带内滤波信号的故障特征频率f1及其倍频2f1及3f1清晰可见，其周围无其他分量干扰，实现了故障的准确诊断，进一步说明了本文方法在检测最佳解调频带方面的可行性。

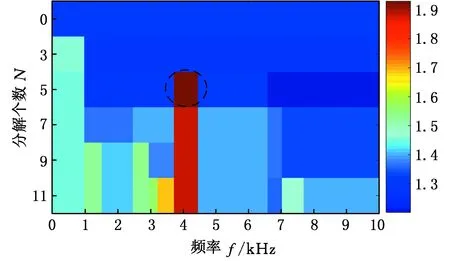
图7 基于自适应Autogram所得仿真信号的峭度图Fig.7 Kurtosis diagram of the simulated signal based on adaptive Autogram

图8 平方包络谱(自适应Autogram)Fig.8 Square envelope spectrum(adaptive Autogram)

为了对比，首先采用基于滤波器组结构的快速谱峭度法对仿真信号进行分析，所得峭度图见图9。由图9可知，最大峭度值对应解调频带的中心频率为7265.625 Hz，带宽为156.25 Hz。计算该频带内信号的平方包络谱，结果如图10所示，相比于自适应Autogram法所得结果，其特征频率被完全淹没，采用该方法无法得到所需故障特征频率，说明该方法无法有效检测到最佳解调频带，导致故障特征频率不明显。

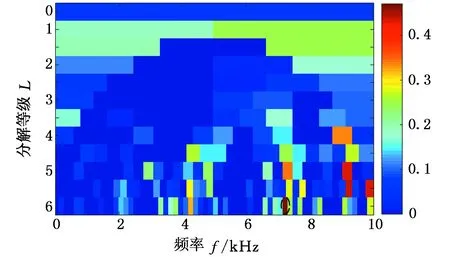
图9 基于快速谱峭度(滤波器组结构) 的仿真信号峭度图Fig.9 Kurtosis diagram of a simulated signal based on fast kurtogram(filter bank structure)

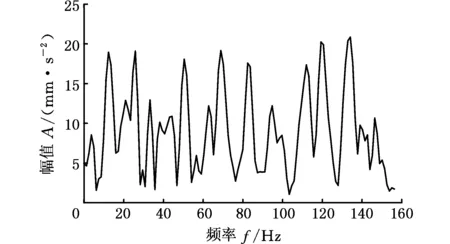
图10 平方包络谱(滤波器组结构)Fig.10 Square envelope spectrum(filter bank structure)

为了对比，采用基于短时傅里叶变换的快速谱峭度计算方法对仿真信号进行分析，所得峭度图见图11。由图11可知，该方法所得最佳解调频带的中心频率为9375 Hz，带宽为39 Hz，位于分解等级的第8级。对该频带内的信号进行分析，得到平方包络谱如图12所示。如同滤波器组结构法处理后得到的结果，其故障特征频率仍然被淹没，说明此方法所得频带并非最佳解调频带。

图11 基于快速谱峭度(短时傅里叶变换) 所得仿真信号的峭度图 Fig.11 Kurtosis diagram of a simulated signal based on fast kurtogram(short time Fourier transform)

图12 平方包络谱(短时傅里叶变换)Fig.12 Square envelope spectrum (short time Fourier transform)

最后，采用原Autogram方法对仿真信号进行分析，得到峭度图见图13。由图13可知，所得频带的中心频率为4687.5 Hz，带宽为625 Hz。对该频带内信号进行分析，得到其平方包络谱如图14所示。由图14可知，相比于快速谱峭度法，其一倍频f1与二倍频2f1较为明显。相比于本文所提方法，其故障特征频率不够明显，周围其他干扰分量较多，尤其在其三倍频3f1处，故障特征频率完全被淹没。以上对比结果说明了所提方法的优越性。

图13 基于原Autogram所得仿真信号的峭度图Fig.13 Kurtosis diagram of a simulated signal based on original Autogram

图14 平方包络谱(原Autogram)Fig.14 Square envelope spectrum(original Autogram)

3 实验分析

为了进一步验证所提诊断方法的可行性与实用性，本节将对实际故障滚动轴承进行诊断分析。实验数据来自安徽工业大学自制滚动轴承模拟故障试验台，如图15所示。实验轴承型号为6206-2RS1 SKF，滚子个数为9，内径30 mm，外径62 mm。使用线切割技术对轴承进行切割。选取滚动轴承内圈切割深度0.4 mm的故障进行实验，如图16所示。实验过程中，设置载荷为5 kN，实际转速为300 r/min，采样频率为8192 Hz，采样时间为20 s。经计算，轴承故障频率fi=27.15 Hz。

图15 滚动轴承模拟故障试验台Fig.15 Simulated fault test bench for rolling bearings

图16 滚动轴承内圈故障Fig.16 Inner ring failure of rolling bearing

首先，采用本文方法对图17所示的实测信号进行分析。实测信号傅里叶谱如图18所示，所得峭度图见图19。由图19可知，当分解个数为13时，检测到最大峭度值对应频带的中心频率为2796.5 Hz，带宽为2599 Hz。为了验证所得频带的准确性，对该频带内信号进一步分析，得到其平方包络谱，如图20所示。由图20可看出，无关分量对特征频率干扰程度低，其故障频率清晰可见，此结果有效验证了自适应Autogram方法的可行性。

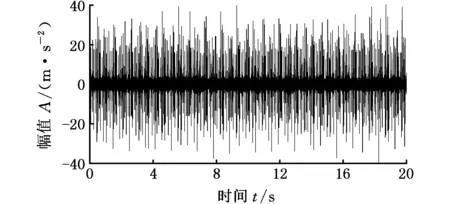
图17 实测信号时域波形图Fig.17 Time domain waveform of measured signal

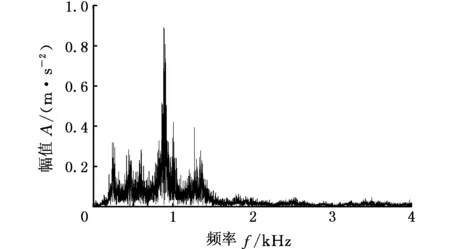
图18 实测信号傅里叶谱Fig.18 Fourier spectrum of measured signal

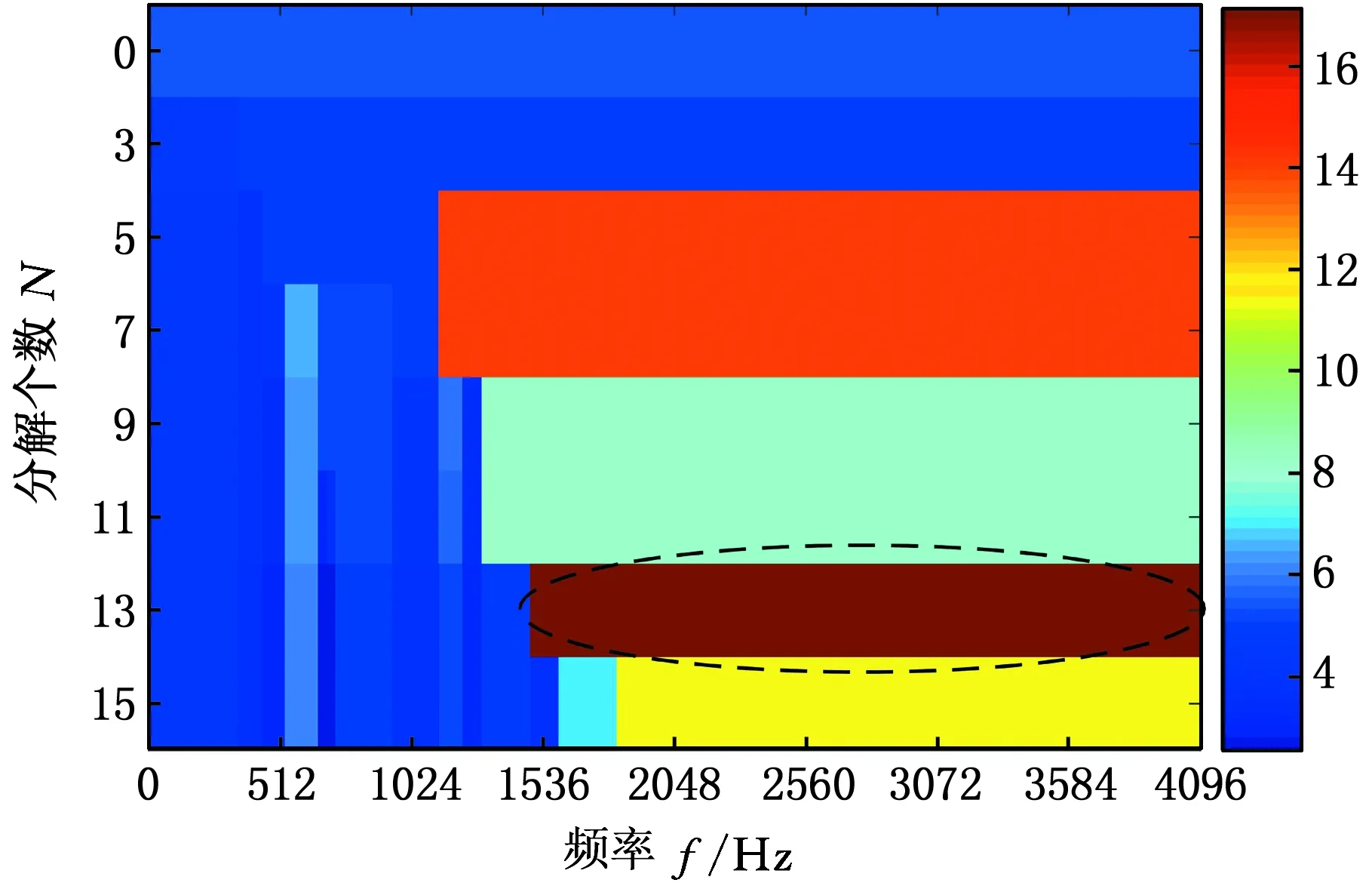
图19 基于自适应Autogram所得实测信号的峭度图Fig.19 Kurtosis diagram of a measured signal based on adaptive Autogram

图20 实测信号滤波后平方包络谱(自适应Autogram)Fig.20 Square envelope spectrum of the filtered measured signal(adaptive Autogram)

为了对比，利用基于滤波器组结构的快速谱峭度法对实测信号进行分析。所得峭度图见图21，检测到最大峭度值对应解调频带的中心频率为2218.6667 Hz，带宽为341.3333 Hz。对该频带内信号进一步分析，得到其平方包络谱，如图22所示。由图22可看出，相比于自适应Autogram法，在二倍频2fi处，周围干扰成分较多，而三倍频完全混淆在无关分量中，故障特征频率不够明显。说明本文方法在检测最佳解调频带效果上强于基于滤波器组结构的快速谱峭度法。

继续采用基于短时傅里叶变换的快速谱峭度法对实测信号进行分析。图23为所得实测信号的频带分布图，可知，最大峭度对应频带的中心频率为3328 Hz，位于分解等级的第4.5级。进一步分析此频带内信号，得到其平方包络谱，如图24所示。由图24可知，一倍频fi处故障特征较为明显，但其他倍频被周围分量淹没，无法进行准确诊断。与所提方法进行比较，其二倍频、三倍频处特征频率不明显，其他分量干扰较大。进一步说明了该方法所选频带并非最优解调频带。

图21 基于快速谱峭度(滤波器组结构) 所得实测信号的峭度图Fig.21 Kurtosis diagram of a measured signal based on fast kurtogram(filter bank structure)

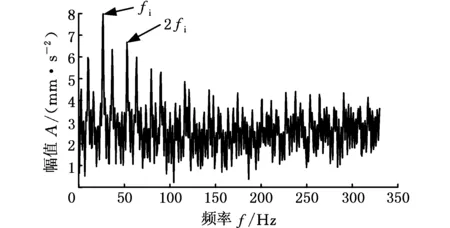
图22 实测信号滤波后平方包络谱(滤波器组结构)Fig.22 Square envelope spectrum of the filtered measured signal(filter bank structure)

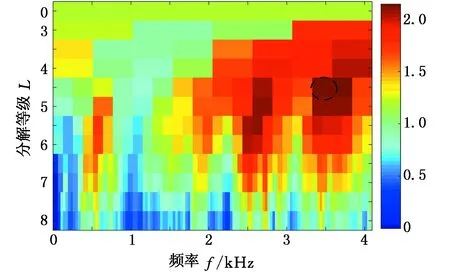
图23 基于快速谱峭度(短时傅里叶变换) 所得实测信号的峭度图Fig.23 Kurtosis diagram of a measured signal based on fast kurtogram(short time Fourier transform)

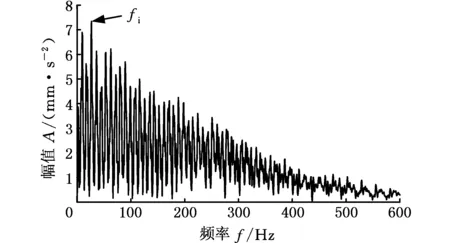
图24 实测信号滤波后平方包络谱(短时傅里叶变换)Fig.24 Square envelope spectrum of the filtered measured signal(short time Fourier transform)

最后，采用原Autogram对实测数据进行分析，图25为所得峭度图。由图25可知，最大峭度对应解调频带的中心频率为2560 Hz，带宽为1024 Hz。对此频带内信号进行分析，得到图26所示的平方包络谱。由图26所知，一倍频fi处故障特征明显。与自适应Autogram法对比，其二倍频、三倍频特征频率不够明显，周围干扰分量较多，因此，该方法所得频带并非最佳解调频带。综上对比，进一步验证了所提自适应Autogram方法的优越性。

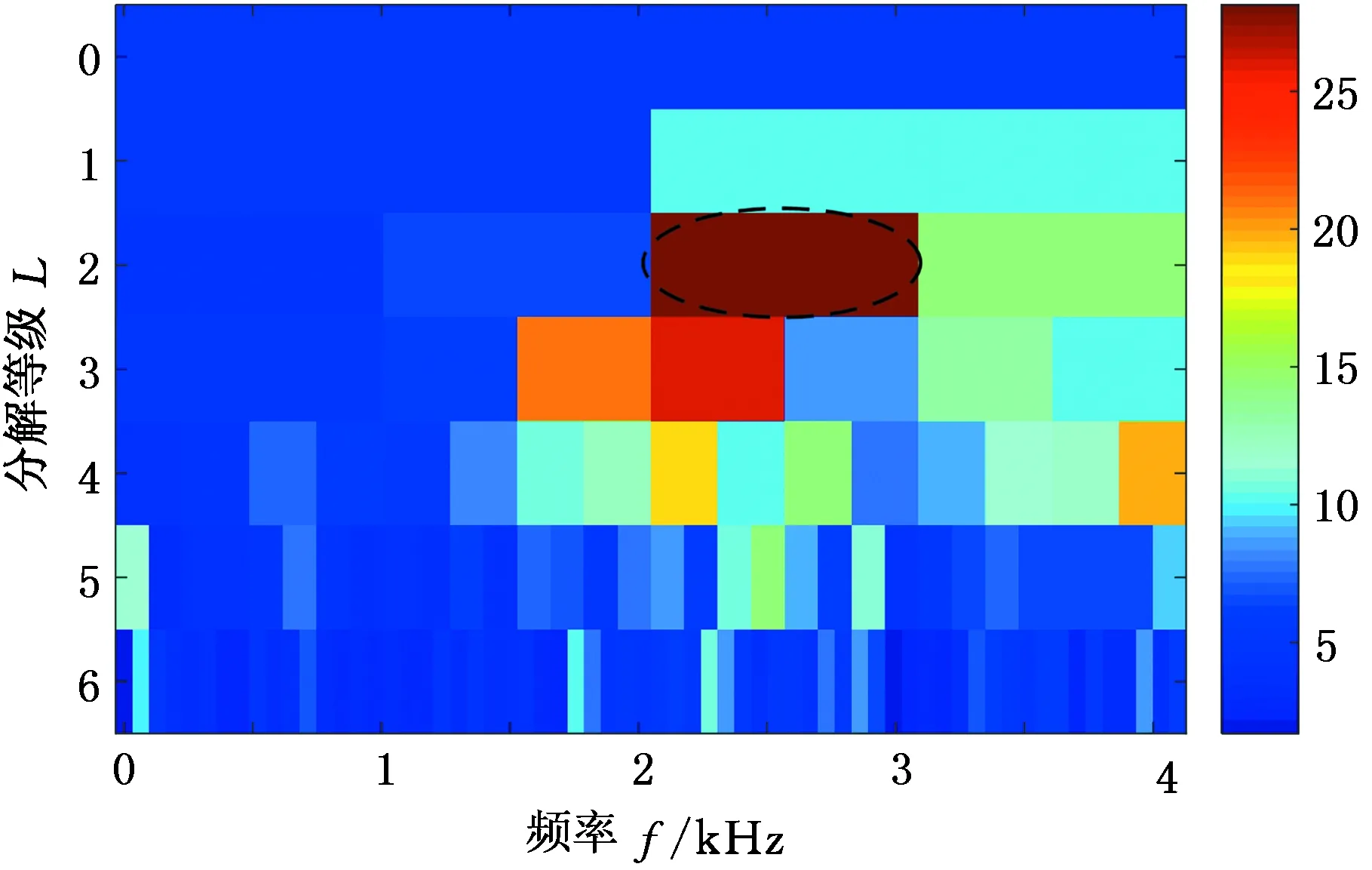
图25 基于原Autogram所得实测信号的峭度图Fig.25 Kurtosis diagram of a simulated signal based on original Autogram

图26 实测信号滤波后平方包络谱(原Autogram)Fig.26 Square envelope spectrum of the filtered measured signal(origial Autogram)

4 结论

针对自相关谱峭度图(Autogram)无法根据信号本身特点自适应划分频带的缺点，提出了一种自适应Autogram方法。新方法在划分频带时，对原始信号的傅里叶包络平滑谱进行划分，通过更改分解个数以得到不同的分割边界，采用经验小波变换重构边界内分量，从而完成频带的自适应分割。通过仿真信号与实测数据分析，并与现有快速谱峭度及Autogram进行对比，得到如下结论：

(1)与快速谱峭度法相比，所提方法能够根据信号本身特点自适应划分频带，最大峭度值对应频带内信号的平方包络谱中，故障特征明显，其频带检测效果强于快速谱峭度。

(2)与原Autogram相比，克服了最大重叠离散小波包变换以二叉树结构划分频带的缺点，同时频带内信号故障特征明显，故障检测效果明显提高。

综上所述，所提方法能够根据原始信号傅里叶谱的特点自适应划分频带，同时故障特征更加明显。但本文仍存在不足之处，如在顺序统计滤波处理过程中，其窗口宽度需事先设定，该问题仍需要进一步研究。