浅谈函数切线的五重境界

山东 王怀兴

与函数切线有关的知识在近几年的高考试题中频繁出现，以2020年与函数切线有关的真题为例，浅谈函数切线的五重境界.

第一重境界：与函数图象上在某点的切线相关

例1.(2020·全国卷Ⅰ理·6)函数f(x)=x4-2x3的图像在点(1，f(1))处的切线方程为

( )

A.y=-2x-1 B.y=-2x+1

C.y=2x-3 D.y=2x+1

【答案】B

【解析】因为f(x)=x4-2x3，所以f′(x)=4x3-6x2，所以f(1)=-1，f′(1)=-2，

因此，所求切线的方程为y+1=-2(x-1)，即y=-2x+1，故选B.

(Ⅰ)当a=1时，求曲线y=f(x)在x=0处的切线方程；

(Ⅱ)若函数f(x)在区间[0,π]上是增函数，求实数a的取值范围.

(Ⅱ)f′(x)=a-x-sinx，因为f(x)在区间[0,π]上是增函数，所以f′(x)≥0在区间[0,π]上恒成立，令a-x-sinx≥0，即a≥x+sinx，令g(x)=x+sinx，则g′(x)=1+cosx≥0，所以g(x)在区间[0,π]上单调递增，所以g(x)max=g(π)=π，故实数a的取值范围是[π,+∞).

解决与函数图象上在某点的切线相关的问题，是教材中最先呈现的，一般明确给出切点.解决此种境界的问题时要注意切点既在曲线上又在切线上，利用函数在切点的导数，求得切线斜率，再利用直线的点斜式方程，求得切线方程.

第二重境界：与函数图象上过某点的切线相关

例2.已知函数f(x)=x3-ax2.当a>3时，求证：过点P(1,f(1))恰有2条直线与曲线y=f(x)相切.

【证明】设过点P(1,f(1))的曲线y=f(x)的切线切点为(x0,y0)，f′(x)=3x2-2ax，f(1)=1-a，

令g(x)=2x3-(a+3)x2+2ax+1-a，则g′(x)=6x2-2(a+3)x+2a=(x-1)(6x-2a)，

x(-∞,1)11,a3 a3a3,+∞ g'(x)+0-0+g(x)↗极大值↘极小值↗

所以过点P(1,f(1))恰有2条直线与曲线y=f(x)相切.

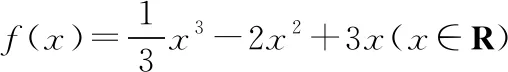
(Ⅰ)求曲线C上任意一点处切线的斜率的取值范围；

(Ⅱ)若曲线C上存在两点处的切线互相垂直，求其中一条切线与曲线C的切点横坐标的取值范围；

(Ⅲ)试问：是否存在一条直线与曲线C同时切于两个不同点？若存在，求出符合条件的所有直线方程；若不存在，说明理由.

【解析】(Ⅰ)f′(x)=x2-4x+3，则f′(x)=(x-2)2-1≥-1，即曲线C上任意一点处切线的斜率的取值范围是[-1,+∞).

(Ⅲ)设存在过点A(x1,y1)的切线与曲线C同时切于两点，另一切点为B(x2,y2)，x1≠x2，

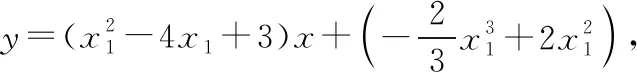
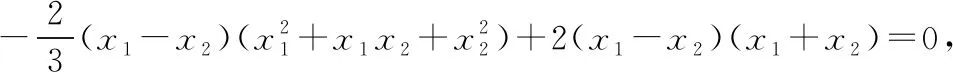
但当x2=2时，由x1+x2=4得x1=2，这与x1≠x2矛盾.所以不存在一条直线与曲线C同时切于两点.

解决与函数图象上过某点的切线相关的问题时，一定要注意此点是切线的切点，也有可能是函数的某条切线经过此点，然后再用第一重境界的方法解决此类问题.务必要考虑全面，切记不要漏解.

第三重境界：与过函数图象外一点的切线相关

例3.过点A(2，1)作曲线f(x)=x3-3x的切线最多有

( )

A.3条 B.2条

C.1条 D.0条

【答案】A

变式3：已知函数f(x)=x3-3x.

(Ⅰ)求函数f(x)的极值；

(Ⅱ)过点P(1,n)，n≠-2，作曲线y=f(x)的切线，问：实数n满足什么样的取值范围，过点P(1,n)可以作出三条切线？

【解析】(Ⅰ)因为f′(x)=3(x2-1)，所以在x=±1处取得极值，极大值f(-1)=2，极小值f(1)=-2.

由g′(x0)=0，得x0=0或x0=1.所以g(x0)在(-∞,0)，(1,+∞)上单调递增，在(0，1)上单调递减.

所以函数g(x0)的极值点为x0=0，x0=1.

故所求的实数n的取值范围是-3

解决与过函数图象外一点的切线相关的问题，一定要明确此点肯定不是切线的切点，所以要先设出此切线在函数某处的切点，再利用函数在切点的导数求得切线斜率.同时，此切线斜率也可以用给出的定点和设出的切点两点坐标表示，然后再利用斜率相等，切点在曲线上解决此种境界的问题.

第四重境界：与过两函数图象交点的切线相关

例4.设函数y=x2-2x+2的图象为C1，函数y=-x2+ax+b的图象为C2，已知C1，C2上存在过C1与C2的一个交点的两切线互相垂直，求a+b的值.

【解析】对于C1：y=x2-2x+2，有y′=2x-2，对于C2：y=-x2+ax+b，有y′=-2x+a，

设C1与C2的一个交点为(x0，y0)，由题意知过交点(x0，y0)的两条切线互相垂直.

变式4：(2018·江苏卷·19)记f′(x),g′(x)分别为函数f(x),g(x)的导函数.若存在x0∈R，满足f(x0)=g(x0)且f′(x0)=g′(x0)，则称x0为函数f(x)与g(x)的一个“S点”.

(Ⅰ)证明：函数f(x)=x与g(x)=x2+2x-2不存在“S点”；

(Ⅱ)若函数f(x)=ax2-1与g(x)=lnx存在“S点”，求实数a的值；

【解析】(Ⅰ)函数f(x)=x，g(x)=x2+2x-2，则f′(x)=1，g′(x)=2x+2.

因此，f(x)与g(x)不存在“S点”.

设x0为f(x)与g(x)的“S点”，由f(x0)=g(x0)且f′(x0)=g′(x0)，得

(Ⅲ)对任意a>0，设h(x)=x3-3x2-ax+a.

因为h(0)=a>0，h(1)=1-3-a+a=-2<0，且h(x)的图象是不间断的，

由f(x)=g(x)且f′(x)=g′(x)，得

此时，x0满足方程组(**)，即x0是函数f(x)与g(x)在区间(0,1)内的一个“S点”.

因此，对任意a>0，存在b>0，使函数f(x)与g(x)在区间(0,+∞)上存在“S点”.

解决与过两函数图象交点的切线相关的问题，一定要注意交点同时在两条曲线上，交点坐标同时满足两个函数的解析式，再对交点分别采用前三个境界涉及的方法，解决此类问题.

第五重境界：与一条直线同时与两函数图象相切相关

( )

【答案】D

(Ⅰ)讨论f(x)的单调性，并证明f(x)有且仅有两个零点；

(Ⅱ)设x0是f(x)的一个零点，证明曲线y=lnx在点A(x0，lnx0)处的切线也是曲线y=ex的切线.

综上，f(x)有且仅有两个零点.

所以曲线y=lnx在点A(x0,lnx0)处的切线也是曲线y=ex的切线.

解决一条直线同时与两函数图象相切相关的问题，一定要注意两个切点分别在两个函数图象上，同时这两个切点又同在这一条直线上，从而得到切点的导数同时等于切线的斜率，并且切点分别在两条曲线上，采用前四个境界涉及的方法，解决此类问题.