数学应用题的常见类型及其解法

山东 秦 振

数学应用题是指用数学的思想方法将一个表面上非数学问题或非完全的数学问题转化为完全数学形式化的问题.应用题的内容十分广泛，解题方法灵活，难度较大、能力要求较高.解应用题需要在陌生的情景中理解、分析所给的问题，并能通过题目中提供的信息，利用化归与转化的数学思想方法将实际问题转化为相应的数学问题，然后选择适当的数学方法解决问题.

解决应用题的思路方法：一是要认真仔细地分析问题，弄清题意，理清问题中的已知条件以及要求解的结论，分清题目中的已知量和未知量及它们之间的关系；二是用数学语言表达实际问题中的相关信息，将实际问题转化为我们熟悉的数学问题——即数学建模；三是将得到的数学模型转化为“常规”的数学问题，然后根据问题的特点选择适当的数学思想方法和解题技巧解决问题，得到相应的结果；四是对得到的结果进行检验，做出解释或预测，给出答案.

下面结合例题介绍应用题的常见类型及其解法.

一、函数的应用

函数知识内容丰富，在现实生活中应用广泛，诸如我们经常遇到的成本最低、利润最高、产出最大、用料最省、效益最大等应用问题，通常可以先转化为函数问题，再利用函数的性质解决.

【例1】如果你有一笔资金用于投资，现在有三种方案供你选择，这三种方案的回报如下：

方案一：每天回报40元；

方案二：第一天回报10元，以后每天比前一天多回报10元；

方案三：第一天回报0.4元，以后每天的回报比前一天翻一番.

请问，你会选择哪种投资方案？

【分析】先根据题意建立三种投资方案对应的函数模型，再比较它们的增长情况，为选择投资方案提供依据.

解:设第x天所得回报是y元，根据题意，可得

方案一:可以用函数f1(x)=40(x∈R+)进行描述；

方案二:可以用函数f2(x)=10x(x∈R+)进行描述；

方案三:可以用函数f3(x)=0.4×2x-1(x∈R+)进行描述.

在同一坐标系分别作出这三个函数图象，如图所示.

由图象可知，每天所得回报，在1～4天，方案一最多，在第5～8天，方案二最多，第9天开始，方案三最多.

天累计回报方案1234567891011一4080120160200240280320360400440二103060100150210280360450550660三0.41.22.8612.425.250.8102204.4409.2818.8

再看累计回报数，如上表所示，投资7天以下(不含7天)，应选择第一种投资方案；投资7天，选择第一、二种方案均可；投资8～10天，应选择第二种方案；投资11天(含11天)以上，则应选择第三种投资方案.

【评注】通过建立相应的目标函数，确定变量的限制条件，利用函数图象、函数变量表以及函数性质，是解决函数型应用问题的基本方法.

二、不等式(组)的应用

数学知识之间的转化基本上就是等量转化和不等关系转化，因此在求某些量的范围或最值时，一般要建立不等式模型.

【例2】建筑学规定，民用住宅的窗户面积必须小于地板面积，但按采光标准，窗户面积与地板面积的比不应小于10%，并且这个比越大，住宅的采光条件越好.问同时增加相等的窗户面积和地板面积，住宅的采光条件是变好了，还是变坏了？请说明理由.

【分析】要确定住宅的采光条件是变好了，还是变坏了，就是要比较原来窗户面积和地板面积的比值与窗户面积和地板面积增加以后的比值谁大、谁小.若是原来的面积比值大，则采光条件变坏了；如果是增加了面积以后的窗户面积和地板面积的比值大，则采光条件变好了.

【评注】本题告诉我们，采光条件的好坏由窗户面积与地板面积比值的大小来衡量，并且是这个比值越大，采光条件越好，但是要注意建筑学的规定：这个比值应小于1.

三、数列的应用

我们熟悉的增长率、存款利息、分期付款、期货贸易、人口增长等实际问题通常可以转化为数列问题，利用数列的有关性质解决.

【例3】学习数学可以使我们更聪明，思维更加缜密.在美国广为流传的一道数学题是：老板给你两种加工资的方案：一是每年增加薪水1 000元；二是每半年增加300元，请选一种.一般不擅长数学的，很容易选择前者.因为一年加1 000元总比两个半年共加600元要多.其实，由于加工资是累计的，时间越长，第二种方案往往更有利.例如在第二年的年末，根据第一种方案可以加得1 000+2 000=3 000(元)，而第二种方案第一年加得300+600=900(元)，第二年加得900+1 200=2 100(元).但是到了第三年，第一方案加得1 000+2 000+3 000=6 000(元)，第二方案加得300+600+900+1 200+1 500+1 800=6 300(元)，比方案一多了300元.第四年、第五年会更多，因此，你若能在该公司工作三年以上，则应该选择第二方案.

根据以上资料，解答下列问题：

(1)如果在该公司工作10年，选择第二方案比第一方案多加薪多少元？

(2)若第二方案改成每半年增加a元，问a为何值时，选择第二方案总是比第一方案多加薪？

【分析】(1)分别计算出两种加薪方案的加薪数额，然后比较.(2)根据题目提供的信息，分别写出第n年末两种方案的加薪数，再根据题意转化为不等式问题解决.

解：(1)在第10年末，由第一方案，得1 000+2 000+3 000+…+10 000=55 000(元).由第二方案，得(300+300×2)+(300×3+300×4)+…+(300×19+300×20)=63 000(元).因为63 000-55 000=8 000(元)，所以在该公司工作10年，选择第二方案比第一方案多加薪8 000元.

【评注】实际问题转化为不等式问题后，往往要结合函数的性质及不等式的性质解决.

四、导数的应用

导数是高中数学的重要内容之一，是解决最优、最大、最小和比较大小等应用问题的有力工具.应用导数解决实际问题的方法是首先建立函数模型，写出函数关系y=f(x)；求出函数的导数f′(x)，解方程f′(x)=0，求出极值点；比较函数在区间端点的函数值的大小，然后确定其最值，给出答案.

【例4】某市环保局调查了该市水泥厂的污染情况.调查发现，水泥厂的烟囱向周围地区散落烟尘造成环境污染.已知A，B两座水泥厂烟囱相距20 km，其中B烟囱喷出的烟尘是A烟囱的8倍.经环境监测表明：落在地面某处的烟尘浓度与该处到烟囱距离的平方成反比，而与烟囱喷出的烟尘量成正比(比例系数均为k).若C是A，B连线上的点，设AC=xkm，C点的烟尘浓度记为y.

(1)写出y与x的函数表达式；

(2)是否存在这样的点C，使该点的烟尘浓度最低？若存在，求出A，C两地的距离；若不存在，请说明理由.

【分析】(1)由AC=x，可得BC=20-x.根据“落在地面某处的烟尘浓度与该处到烟囱距离的平方成反比，而与烟囱喷出的烟尘量成正比(比例系数均为k).”可得函数表达式.(2)利用导数法讨论函数的最小值.

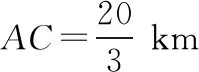
【评注】应用导数法解决实际问题，首先要根据题意确定自变量的取值范围，注意极大值与最大值的关系，还要验证函数在区间端点所对应的函数值的大小.

五、三角函数的应用

有些涉及几何图形、角度、航海、测量等方面的问题，可以转化为三角函数问题，利用三角函数的性质解决.

【例5】某监控室的工作人员，主要是根据仪表的数据变化加以操作控制的，若仪表高m米，底边距地面n米，如图所示，工作人员坐在椅子上眼睛距地面的高度为1.2米(n>1.2)，问工作人员坐在什么位置看得最清楚？

【分析】工作人员观察仪表看得最清楚的位置，就是使∠BAC达到最大时点A的位置.由于∠BAC是锐角，因此要使它最大，可以转化为该角的正切最大，即tan∠BAC最大.

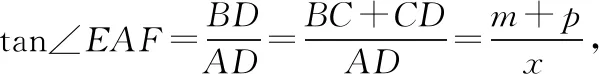
【评注】三角函数在测距、测角等方面的应用比较广泛，也是最常见的问题.在解决此类应用问题时，应熟悉视角、方位角、仰角、俯角等概念，并能熟练应用三角函数的性质解决有关问题.另外，可以研究在家看电视时，坐在什么位置看得最清楚.

六、线性规划的应用

在生活实践中，经常遇到给定人力、物力、财力资源，让我们应用这些资源，获得最大效益；或者给定一项任务，完成任务的人力、物力、财力最小.这些实际问题往往需要应用线性规划解决.

【例6】某营养师要为某个儿童预定午餐和晚餐.已知一个单位的午餐含12个单位的碳水化合物，6个单位的蛋白质和6个单位的维生素C；一个单位的晚餐含8个单位的碳水化合物，6个单位的蛋白质和10个单位的维生素C.另外，该儿童这两餐需要的营养中至少含64个单位的碳水化合物，42个单位的蛋白质和54个单位的维生素C.如果一个单位的午餐、晚餐的费用分别是2.5元和4元，那么要满足上述的营养要求，并且花费最少，应当为该儿童分别预定多少个单位的午餐和晚餐？

【分析】根据题意设出相关变量建立线性约束条件、目标函数，利用线性规划的有关知识，作出可行域，找出最优解，再还原为实际问题.

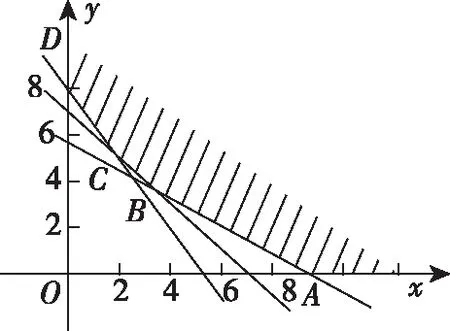
【评注】线性规划的最优解往往取在边界直线的交点处，另外，解决这类问题的易错点是在列约束条件时漏掉x>0，y>0，且它们都是正整数.

七、解析几何的应用

这类问题通常涉及桥梁、隧道、反光灯、通风塔、人造卫星运行轨迹等实际问题.解决这类问题的方法是首先弄清题意，建立合理的坐标系，将等量关系转化为相应的方程(组)，研究曲线方程得到结论.

【例7】为了在神舟六号飞船返回舱顺利到达地球后及时将航天员安全救出，地面指挥中心在返回舱预计到达区域安排三个救援中心(记为A，B，C)，A在B的正东方向，相距6千米，C在B的北偏西30°方向，相距4千米，P为航天员着陆点，某一时刻，A接收到P的求救信号，由于B，C两地比A距P远，因此4秒后，B，C两个救援中心才同时接收到这一信号.已知该信号的传播速度为1千米/秒.

(1)求在A处发现P的方位角；

(2)若信号从P点的正上空Q点处发出，则A，B收到信号时间差变大还是变小？说明理由.

【分析】根据题意，利用“某一时刻，A接收到P的求救信号，由于B，C两地比A距P远，因此4秒后，B，C两个救援中心才同时接收到这一信号”转化为方程，构建解析几何模型解决.

解：(1)因为|PC|=|PB|，所以P点在线段BC的垂直平分线上，又因为|PB|-|PA|=4，所以P点在以A，B为焦点的双曲线的右支上.以线段AB中点为原点，AB所在直线为x轴建立直角坐标系，如图所示，

(2)如图所示，

【评注】由于B，C两地比A地接收到的信号慢4秒，即|PB|-|PA|=4，满足双曲线的定义，据此建立双曲线模型，使实际问题转化为解析几何问题.这类问题在建立数学模型时，要分清物体的运动形式和曲线的形状符合哪一种圆锥曲线的定义或图形，再根据题意转化为相应的曲线方程.

八、立体几何的应用

在工作、生活中经常遇到空中观测、地球的经纬度等实际背景下几何体的截面积、表面积和体积的计算，以及空间位置关系的确定等问题，这些实际问题一般都能利用立体几何模型解决.

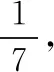
【评注】在解决几何体问题中，所给“数据”一般要转化到一个三角形中，因此特征三角形的构建是解题的重点，而构建特征三角形一般从几何体的高及斜高入手，如本题中的△ABC.另外，本题在求出体积后，因为所求的“降雨的降水量”要用到水的体积的不变性，因此根据题意把台体转化为柱体，进而求出降水量.

九、概率统计的应用

这类问题的背景可以是当前的社会热点问题，也可以是某些“常规”问题，其特点是需要用概率与统计的基础知识和基本方法解决.解决此类问题的方法是分析问题的要求，弄清题意，建立相应的统计与概率模型，然后选择适当的方法和性质解决.

【例9】工作人员需要进入核电站完成某项具有高辐射危险的任务，每次只派一个人进去，且每个人只派一次，工作时间不超过10分钟.如果前一个人10分钟内不能完成任务则撤出，再派下一个人.现在一共只有甲、乙、丙三个人可派，他们各自能完成任务的概率分别为p1，p2，p3，假设p1，p2，p3互不相等，且假定各人能完成任务的事件相互独立.

(1)如果按甲最先、乙次之、丙最后的顺序派人，求任务能被完成的概率.若改变三个人被派出的先后顺序，任务能被完成的概率是否发生变化？

(2)若按某指定顺序派人，这三个人各自能完成任务的概率依次为q1，q2，q3，其中q1，q2，q3是p1，p2，p3的一个排列，求所需派出人员数目X的分布列和均值(数学期望)E(X).

(3)假定1>p1>p2>p3，试分析以怎样的先后顺序派出人员，可使所需派出的人员数目的均值(数学期望)最小.

【分析】(1)直接计算比较复杂，可以考虑问题的“反面”；(2)根据题意列出随机变量X的分布列，再利用公式计算E(X)；(3)根据“经验”，优先派出完成任务概率大的人，可减少所需派出的人员数目的均值；然后证明.

解：(1)无论以怎样的顺序派出人员，任务不能完成的概率都是(1-p1)(1-p2)(1-p3)，所以任务能完成的概率与三个人被派出的先后顺序无关，并等于1-(1-p1)(1-p2)(1-p3)=p1+p2+p3-p1p2-p2p3-p3p1+p1p2p3.

(2)当依次派出的三个人各自完成任务的概率分别为q1，q2，q3时，随机变量X的分布列为

X123Pq1(1-q1)q2(1-q1)(1-q2)

所需派出的人员数目的均值(数学期望)是E(X)=q1+2(1-q1)q2+3(1-q1)(1-q2)=3-2q1-q2+q1q2.

(3)由(2)的结论可知，按甲最先、乙次之、丙最后的顺序派人时，E(X)=3-2p1-p2+p1p2.根据经验，优先派出完成任务概率大的人，可减少所需派出的人员数目的均值.下面证明：对于p1,p2,p3的任意排列q1,q2,q3，都有3-2q1-q2+q1q2≥3-2p1-p2+p1p2.

因为(3-2q1-q2+q1q2)-(3-2p1-p2+p1p2)=2(p1-q1)+(p2-q2)-p1p2+q1q2=2(p1-q1)+(p2-q2)-(p1-q1)p2-q1(p2-q2)=(2-p2)(p1-q1)+(1-q1)(p2-q2)≥(1-q1)[(p1+p2)-(q1+q2)]≥0，所以不等式成立.

因此当(q1,q2,q3)=(p1,p2,p3)时，E(X)得到最小，即完成任务概率大的人优先派出，可减小所需派出人员数目的均值.

【评注】此题考查了相互独立事件的概率计算，离散型随机变量及其分布列，均值等基本知识，同时考查了在现实生活中处理问题的能力以及抽象归纳能力、合情推理与演绎推理能力，还考查了数学化归与转化思想和分类讨论思想.