等腰三角形中的易错点分类

文 李青

在初中数学中，三角形一直是重要的学习内容，等腰三角形更是重中之重。等腰三角形的许多问题需要用分类讨论的方法去解决，同学们往往会在解题过程中，由于审题不清、知识点掌握不牢或考虑不全面等原因造成“错解”。为避免同学们再次出现此类问题，下面老师对于常出现的一些易错点进行分析，希望对同学们有所帮助。

一、等腰三角形上的高

例1在等腰三角形ABC中，AD⊥BC，交直线BC于点D，若求△ABC的顶角的度数。

【分析】解决此类问题应关注两点：①没有明确是腰上的高还是底边上的高，应分类讨论；②对于等腰三角形腰上的高，还应按形内和形外分类。此题中我们应该把BC分为腰和底两种情况来讨论：当BC为底边时，其高AD始终在三角形的内部；但当BC为腰时，应按高在三角形内和三角形外两种情况来讨论。

解：（1）当BC为底时，如图1。

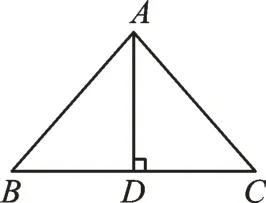
图1

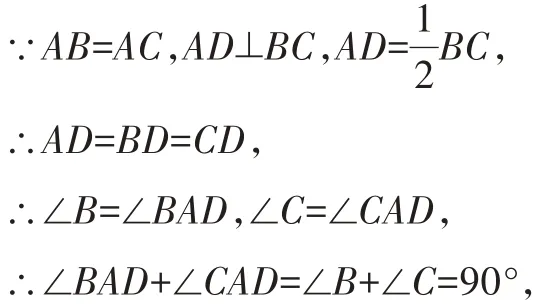
∴顶角∠BAC=90°。

（2）当BC为腰时。

①如图2，AD在△ABC内部时，

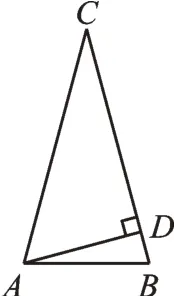
图2

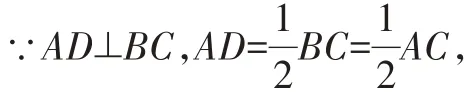
∴顶角∠C=30°；

②如图3，AD在△ABC外部时，

图3

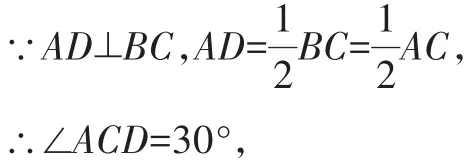
∴顶角∠ACB=180°-30°=150°。

所以△ABC的顶角的度数为30°或90°或150°。

二、等腰三角形腰上的垂直平分线

例2在△ABC中，AB=AC，AB边上的垂直平分线与AC所在的直线相交所得的锐角为50°，则底角∠B=。

【分析】求解本题时，由于不确定△ABC的形状，于是需要分∠A为锐角和钝角两种情况进行分析。画出图形，利用数形结合的方法，易求出底角∠B的度数为70°或20°。

【正确答案】70°或20°。

三、等腰三角形腰上的中线

例3等腰三角形一腰上的中线把等腰三角形的周长分成15和6两部分，求这个等腰三角形的腰长及底边长。

【分析】等腰三角形的中线把三角形的周长分成了15和6两个部分，它们的差值是由于腰和底的长不同而产生的，但不能确定腰和底谁长谁短，所以要分情况讨论。解决这类问题时，一般用设未知数的方法会比较简单，但一定要注意检验其结果是否符合三角形的三边关系。

解：设腰长为x，底边长为y。

（1）若腰比底长，由题意，

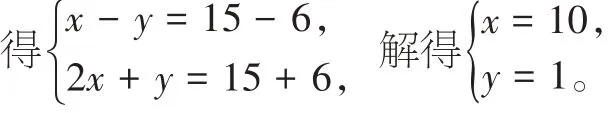
（2）若底比腰长，由题意，

而4+4＜13，故舍去，所以这个三角形的腰长为10，底边长为1。

小试牛刀

1.在等腰三角形ABC中，∠A的外角为100°，那么∠B=。

2.在等腰三角形ABC中，∠A=30°，AB=8，则AB边上的高CD的长为 。

3.在平面直角坐标系中，点A的坐标为（3，4），连接OA，在x轴上找一点B，使得△OAB是等腰三角形，则点B的坐标为 。