从头算价键理论的研究进展

吴 玮，郑培锟

(厦门大学化学化工学院，固体表面物理化学国家重点实验室，福建省理论与计算化学重点实验室，福建 厦门 361005)

建立在量子力学基础上的现代化学键理论可以分为两类：一类是基于离域分子轨道的分子轨道理论，另一类是基于定域原子轨道的价键理论.这两类方法几乎同时发展于20世纪20年代，在发展的早期30年间，价键理论由于其电子两两配对形成化学键的概念与经典的化学键思想吻合，在化学键本质研究中扮演着主要角色.Pauling应用他自己发展的共振论，通过共价-离子叠加、共振、杂化等概念，成功地解释了当时几乎所有分子的化学键性质[1-2].Wheland应用共振论讨论了有机化学的诸多化学反应[3].然而自20世纪50年代以来，从头算水平的分子轨道理论迅速占据了化学键理论研究的主导地位，经过70多年的发展取得了巨大成功，分子轨道理论几乎成为量子化学波函数方法的代名词.基于正交分子轨道的量子化学计算方法非常丰富，包括了基于单参考的波函数方法和多参考波函数方法.这些计算方法已经可以满足不同计算精度和不同分子体系复杂性的要求.此外，基于Kohn-Sham轨道的KS-DFT(Kohn-Sham density functional theory)方法由于其计算代价的经济性和可接受的计算精度的优点而广受欢迎，特别是在生物化学和材料科学等学科领域[4-5].相比之下，由于采用原子轨道作为单电子函数，以及复杂的体系多电子波函数表达形式，价键理论方法的计算量非常巨大，价键理论的从头算应用研究几乎不现实.庆幸的是，随着计算机科学技术的发展，高性能科学计算能力不断提高，价键理论从头算已经成为可能.自20世纪70年代以来，从头算价键理论方法的发展开始引起人们的兴趣，采用价键结构作为组态函数的多电子理论方法陆续被提出，基于价键理论的量子化学计算应用逐渐丰富.本文对过去40年来从头算价键理论的研究进展进行简要的回顾，侧重于计算方法和算法的发展，特别是厦门大学化学键理论研究团队(下文称本团队)的研究工作.

1 价键理论中的多电子波函数

价键理论的发展可追溯到1916年Lewis[6]发表的著名论文，在论文中Lewis提出了电子配对的概念.随着量子力学的诞生，Heitler和London[7]在1927年首次将量子理论应用于氢分子.随后Slater[8-9]以行列式的形式描述价键函数，并推广到多电子分子体系.与此同时，Pauling[1-2]发展了多原子分子量子理论，建立了Lewis的化学键理论与量子力学间的联系，并提出了一系列重要的化学键概念，包括价键结构共振、轨道杂化等.由于Heitler、London、Slater和Pauling在早期对价键理论发展的贡献，价键理论中的多电子波函数通常称为HLSP(Heitler-London-Slater-Pauling)函数.

由于价键理论选用定域形式的原子轨道作为分子体系的单电子函数，采用对应于经典价键结构的波函数作为多电子波函数的态函数，计算结果与经典化学键理论建立联系，可以直接为化学家提供直观的化学图像解释.然而，由于不同原子之间原子轨道的非正交性，从头算水平下的价键理论方法的数学形式相当复杂.在从头算分子轨道理论中，最简单的计算方法是Hartree-Fock方法[8,10-11]，其波函数表示为一个Slater行列式.然而，即使在价键理论计算中只采用一个价键结构，其Slater行列式的个数是2m，其中m为价键结构中的共价键个数，即价键理论方法属于多行列式的波函数方法.因此，相比于单参考的分子轨道理论计算方法，入门级的价键理论计算代价非常高.鉴于此，虽然价键理论在早期的发展非常成功，但在追求复杂分子体系精确计算的今天，仍无法直接应用于开展电子结构理论从头算研究.

除了HLSP函数的行列式展开数目随分子的成键数呈指数增长而导致的计算困难，即所谓2m困难外，价键理论计算的第二困难是由于不同原子间的轨道不正交导致的一个轨道积分包括N！项的基函数积分，即所谓的“N！困难”.

显而易见，克服第一困难的直接方法是回避HLSP函数，采用其他简单的多电子函数形式.Goddard在20世纪70年代发展了广义价键(generalized valence bond, GVB)方法[12-17].通过轨道的强正交条件，并选用极少的组态函数简化计算.随后，他们进一步简化体系波函数，只考虑一个组态函数，称为GVB-PP(generalized valence bond-perfect paring)方法.GVB-PP方法采用离域的原子轨道，即虽然轨道保持原子轨道的形式主要定域在特定的原子上，但其他原子的基函数仍然有微小的贡献.这类轨道称为重叠加强轨道(overlap-enhanced orbital,OEO).由于轨道的离域，GVB-PP方法将离子结构的贡献隐性地包括在体系的多电子波函数内.进而通过将GVB-PP波函数表示为双占据自然轨道的Slater行列式，GVB-PP方法巧妙地克服了由非正交轨道引起的“N！困难”.

Gerratt、Raimondi和Cooper发展了自旋耦合价键(spin-coupled valence bond, SCVB)方法[18-24].该方法采用HLSP函数作为波函数，与GVB方法相似，价键轨道选用OEO形式，但是解除了轨道的强正交条件；选用一个电子轨道组态，但包括所有的电子自旋耦合方式，即考虑了所有的共价键结构.和GVB方法相似，由于选用OEO轨道形式，SCVB波函数隐性地包括了离子结构的贡献.SCVB方法的后续发展包括多组态的SCVB方法和微扰理论的应用[25-26].

因为选用OEO轨道，GVB和SCVB方法的波函数无需包括离子结构的HLSP函数，所以可以有相当紧凑的多电子波函数形式.然而这种波函数的选用偏离了早期价键理论的初衷，特别是共振论，因为共价-离子共振是共振论中一个最重要的概念.人们通常将采用OEO形式的方法称为现代价键理论，以区别于早期的价键理论方法.为了在从头算水平上忠实地描述早期的价键理论，必须采用严格定域的原子轨道，将价键轨道展开为以特定原子(或碎片)为中心的基函数的线性组合，这类轨道称为杂化原子轨道(hybrid atomic orbital, HAO).基于HAO的价键理论从头算方法通常称从头算经典价键(abinitioclassical valence bond)理论.需要指出的是，现代价键方法和经典价键方法各有特点，在具体计算应用中，必须根据不同的研究动机选用不同的研究方法[27-29].

由Mo等[30-35]发展的块定域波函数(block-localized wavefunction,BLW)是一种极简的价键理论方法.BLW方法根据研究目的将分子分为不同的块，轨道定域于特定的块上，同一块上的轨道相互正交，而不同块之间的轨道不正交.BLW方法的多电子波函数采用一个Slater行列式，回避了HLSP函数的多行列式困难；同时利用轨道的定域性使得BLW函数对应于特定的价键结构.相比于采用HLSP函数的价键方法，BLW方法的计算代价很低，可以应用于大分子体系，目前已广泛应用于分子的电子转移等问题的研究[34,36-38].

Gallup等[39]提出基于对称群投影算符的表函数作为体系多电子波函数.一个表函数表示为若干个行列式的线性组合，且对应于经典价键结构.由于构造表函数所需的行列式个数远小于HLSP函数所需的数目，表函数方法的计算量小于基于HLSP函数的价键计算方法.遗憾的是，虽然表函数一一对应于HLSP函数，但是不等同于HLSP函数，其计算结果无法严格描述经典价键理论.

简要地说，价键理论方法中的多电子波函数分为两类：一类是忠实于描述经典价键理论的HLSP函数，另一类是为了回避HLSP函数的复杂性选用的其他简单函数形式.在下文中，主要讨论基于HLSP函数的价键理论计算方法.

2 价键理论计算方法

由于从头算价键理论方法数学形式的复杂性，其发展非常缓慢，相关计算应用也无法和分子轨道理论方法相比.然而，作为量子化学的波函数方法，采用与分子轨道理论中相似的处理策略，价键理论同样拥有对应的计算方法.在这一节中简要地介绍目前已有的价键理论从头算方法，包括价键自洽场(valence bond self-consistent field,VBSCF)、呼吸轨道价键(breathing orbital valence bond,BOVB)、价键组态相互作用(valence bond configuration interaction,VBCI)、价键二阶微扰理论(valence bond second-order perturbation theory,VBPT2)、密度泛函价键(density functional valence bond,DFVB)，以及溶液环境下的价键理论计算方法.图1所示为目前可用于实际化学问题研究的价键计算方法.

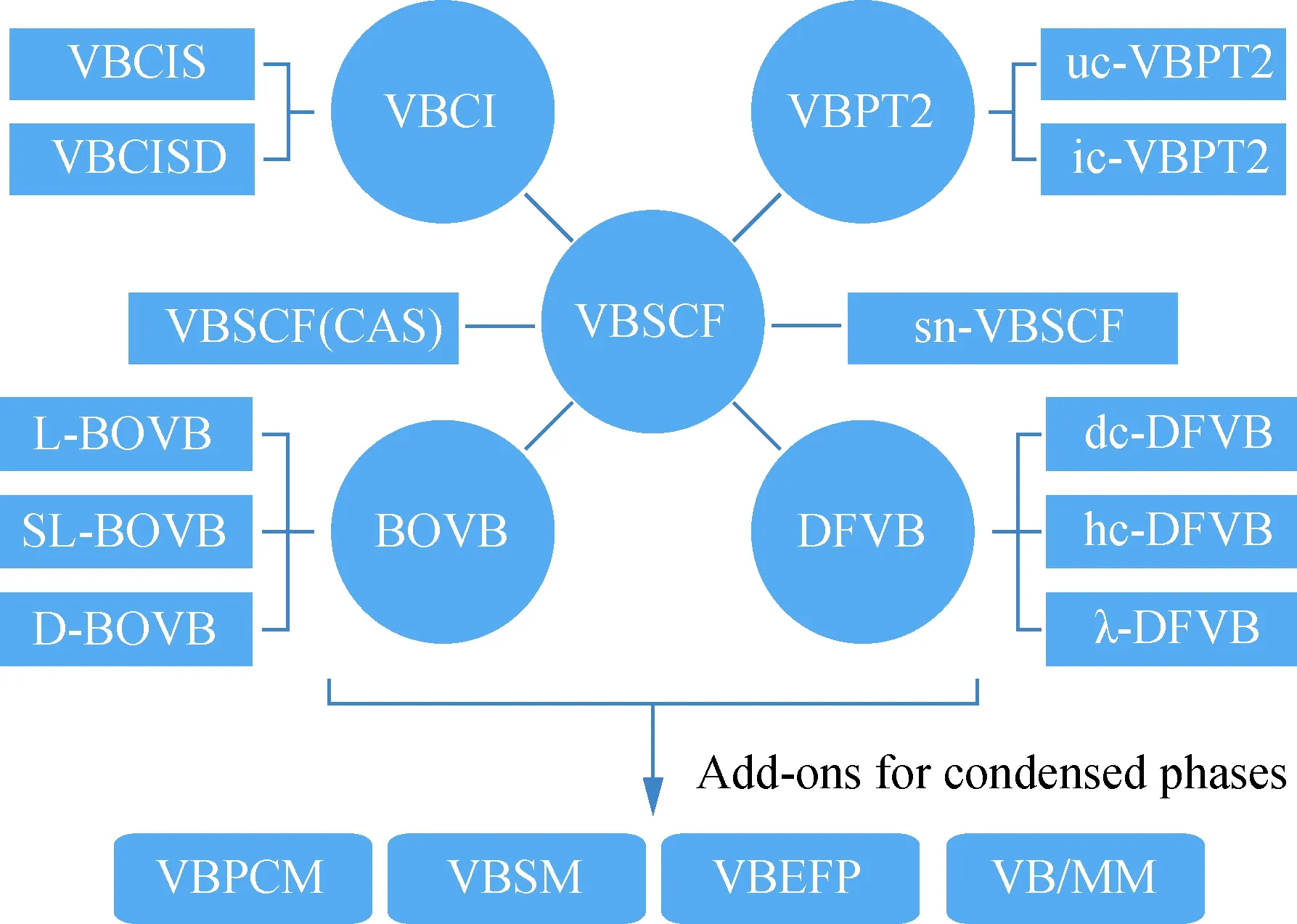
VBSCF(CAS).完全活性空间价键自洽场；VBPCM.价键极化 连续模型；VBSM.价键溶剂化模型；VBEFP.价键有效碎片势； VB/MM.价键理论/分子力学；L.localized;D.delocalized; SL.split;uc.uncontracted;ic.internally contracted; sn.seniority number;dc.dynamic corrected; hc.Hamiltonian-corrected.图1 可用的经典价键方法Fig.1 Available classical valence bond methods

2.1 VBSCF方法

在20世纪70年代由van Lenthe和Balint-Kurti[40-41]发展的VBSCF方法被视为是首个从头算经典价键方法.在VBSCF方法中，体系多电子波函数轨道采用基于HAO的HLSP函数，一个HLSP函数对应于一个经典价键结构，轨道系数和结构系数同时优化以获取最低的体系总能量.VBSCF方法的数学形式与分子轨道理论的多组态自洽场(multi-configuration self-consistent field,MCSCF)方法相似，区别在于前者采用由非正交原子轨道构造的HLSP函数，而后者采用基于正交分子轨道的组态函数(configuration state function,CSF).当体系多电子波函数选取所有线性独立的HLSP函数且价键轨道为OEO时，VBSCF波函数完全等价于分子轨道理论的完全活性空间自洽场(complete active space self-consistent field,CASSCF)波函数[42].

2.2 BOVB方法

与CASSCF方法相似，VBSCF方法缺少对电子动态相关效应的描述.20世纪90年代，Hiberty等[43-45]发展了BOVB方法.该方法选用了与VBSCF方法相同的HLSP函数构造体系多电子波函数，但是与VBSCF不同的是，每个HLSP函数都有各自的优化价键轨道.例如对于氟分子，共价结构的成键轨道与离子结构中阴离子的双占据轨道不完全相同，即在这两个轨道的基函数展开中，相同基函数的展开系数可以不完全相同.由于BOVB方法中轨道的优化考虑了各价键结构中轨道的极化，具有更高的优化自由度，BOVB的体系能量包括部分动态相关，特别是与化学键直接相关的动态相关能.BOVB方法包括不同计算级别，如L-BOVB、D-BOVB和SL-BOVB等[45].BOVB方法在不增加多电子波函数形式复杂性的前提下，极大程度地提高了VBSCF方法的计算精度.由于在VBSCF计算中的同一个轨道在BOVB中的不同结构可以有不同的优化系数，这个自由度常导致BOVB计算中的收敛困难，在实际计算中应小心处理.

2.3 VBCI方法

在分子轨道理论中，通过引入激发组态的后自洽场方法可以有效地描述电子动态相关，最重要的后自洽场技术包括组态相互作用、微扰方法和耦合簇方法.本团队将组态相互作用方法应用于价键理论，提出了VBCI方法[46-47].在VBCI方法中，为了涵盖电子动态相关，引入激发HLSP函数.激发HLSP函数由VBSCF的HLSP函数(称基础HLSP函数)产生，其中基础HLSP函数的价键轨道(称为占据轨道)被价键空轨道替代.虽然在VBSCF计算中，引入价键空轨道用于轨道优化，但是VBSCF能量不受空轨道定义的影响，然而不同定义的价键空轨道将得到不同的后价键自洽场(post-VBSCF)波函数，最后决定post-VBSCF的计算结果.为此需要定义价键空轨道，在VBCI方法中空轨道通过轨道投影算符对角化得到.为了获得严格对应于经典价键结构的激发HLSP函数，与价键占据轨道一样，价键空轨道是严格定域在原子上的，定域在同一原子上的空轨道和占据轨道相互正交，而属于不同原子的轨道不正交.不同于分子轨道理论的组态相互作用方法，VBCI波函数仅包括同一原子内的占据轨道到空轨道的激发.一旦构造完成激发HLSP函数及其Hamiltonian矩阵计算，通过求解久期方程就可以得到VBCI能量.目前VBCI方法包括单重电子激发的VBCIS方法和同时单双重电子激发的VBCISD方法.测试结果表明，VBCIS方法的精度与BOVB方法一致，而VBCISD方法与单双重激发偶合簇(coupled-cluster singles and doubles,CCSD)方法相当.

2.4 VBPT2方法

量子化学中的微扰理论是一种经济有效的描述动态相关的计算手段.本团队将微扰理论应用于价键理论计算，提出了VBPT2方法[48-49].在VBPT2方法中，VBSCF波函数作为零级参考函数，将一级校正波函数表示为单双重激发HLSP函数的线性组合，应用Rayleigh-Schrödinger微扰理论，计算得到VBPT2的体系能量和相应波函数.与VBCI方法不同，为了追求计算效率，VBPT2方法中空轨道是全离域的，与所有占据价键轨道正交.因此，VBPT2中的激发HLSP函数不严格对应于经典价键结构.

目前存在两个不同版本的VBPT2方法，早先的版本是通过对基础HLSP函数的激发定义体系的一级校正波函数.近年来，本团队发展了价键理论的约化密度矩阵方法[49-52]，应用内收缩技术，将约化密度算法作用于体系VBSCF波函数获取一级校正波函数.基于内收缩的VBPT2方法具有更高的计算效率，计算精度与前者一致.如同VBSCF与CASSCF之间的关系，当计算包括所有线性独立的价键结构且选取OEO轨道时，VBPT2与完全活性空间二阶微扰理论(complete active space second-order perturbation theory,CASPT2)[53]完全等价.在实际计算中，选用紧凑的VBSCF波函数所获得的VBPT2计算结果具有与CASPT2一致的计算精度.

2.5 DFVB方法

KS-DFT是当前最成功的量子电子结构理论计算方法之一.相比于Hartree-Fock方法，KS-DFT方法以相同的计算量实现了对体系电子动态相关的描述[4-5].然而，由于采用单行列式形式，KS-DFT仍然无法正确地描述体系的静态相关.显然，将KS-DFT与VBSCF方法结合有望同时获得对体系静态和动态相关的合理描述.本团队先后提出了VBDFT(s)[54-57]、VB-DFT[58]和DFVB[59-61]等方法，其中VBDFT(s)是Hückel型半经验价键方法，经验参数由DFT计算获得.VB-DFT方法通过芯价分离，DFT用于体系芯部分的计算，而成键价电子采用价键理论方法处理.DFVB方法通过VBSCF计算获得体系波函数和包括静态相关的体系总能量，采用KS-DFT计算体系动态相关能，目前包括不同的处理方案：dc-DFVB[59]、hc-DFVB[60]和λ-DFVB[61].测试计算表明，最新发展的λ-DFVB方法的计算精度与CASPT2方法相当.

2.6 溶液环境下的价键理论计算方法

作为量子化学的波函数方法，价键理论方法提供了以HLSP函数为态函数的多电子波函数.与分子轨道理论方法相似，结合溶剂模型理论方法，价键理论可以实现在溶液环境下的量子化学计算.本团队结合极化连续模型(polarizable continuum model,PCM)提出了VBPCM方法[62]，结合基于广义波恩近似的溶剂化模型(solvation model,SM)发展了VBSM方法[63]，结合有效碎片势(effective fragment potential,EFP)发展了VBEFP方法[64]，其中VBPCM和VBSM属于隐性溶剂模型方法，而VBEFP方法是显性溶剂模型方法.在组合量子力学和分子力学框架下，本团队发展了VB/MM方法[65].价键理论不仅与分子轨道理论方法一样，可以处理体系基态的溶剂化效应，同时可以描述溶剂对各个经典价键结构的影响.

3 价键理论方法中的矩阵元计算

在从头算价键理论方法中，体系波函数表示为HLSP函数的线性组合.为了计算体系总能量和各类性质，需要计算HLSP函数之间的Hamiltonian和重叠矩阵元.在VBSCF和BOVB方法中，价键轨道的优化需要矩阵元的梯度和Hessian矩阵.此外，post-VBSCF方法的计算涉及基础HLSP函数与激发HLSP函数间矩阵元的计算.

如上文所述，从头算价键理论的两大困难包括：基于HLSP函数的价键理论天然属于多参考波函数方法；采用原子轨道导致轨道的不正交性.前者类似于CASSCF方法，计算标度远高于基于单参考的分子轨道波函数方法；而更为严重的是，轨道的不正交性导致行列式矩阵元的计算不能应用Condon-Slater规则,产生所谓的“N！困难”.为了克服直接展开方法的“N！困难”，传统的计算方法于20世纪50年代由Löwdin提出[66]，随后方法得到不同程度的改进[50-51,67-70].

20世纪80年代,人们试图在量子化学的多电子酉群方法(unitary group approach,UGA)和对称群方法(symmetric group approach,SGA)框架内解决“N！困难”，McWeeny[67]和张乾二等[68-69,71]同时提出了基于对称群表示理论的无自旋价键理论方法，应用标准投影算符构造体系多电子波函数，克服传统方法的2m行列式困难.进而本团队在20世纪90年代提出了对不变式行列式(paired-permanent-determinant,PPD)方法[69,72].在该方法中，对于一个给定的方阵，PPD的定义类似于行列式，包括与行列式完全相同的N！项矩阵元乘积，它们的区别在于每一项的系数，其中PPD的展开系数由对称群的不可约表示矩阵元决定.一个HLSP函数表示为一个PPD函数，其计算通过类似于行列式的拉普拉斯展开进行.虽然PPD方法的数学形式紧凑，但是在实际计算中拉普拉斯展开并不是一个有效的算法.

如果说从头算价键理论中的矩阵元计算相当耗时，那么能量梯度和Hessian的计算更加困难.传统的方法是应用广义Brillouin定理[73]，将梯度表示为价键结构与激发价键结构之间的矩阵元计算.本团队提出了基于广义Fock矩阵的能量对轨道系数的梯度计算解析方法[70]，将行列式间的矩阵元的梯度计算标度降到m4，其中m为基函数个数；同时该方法无需将基函数积分变换为轨道积分，大幅度减低了计算标度.

为了进一步降低计算标度，近10年来，本团队发展了价键理论的约化密度矩阵方法，通过采用张量分析语言，引进轨道重叠积分作为度规张量，将价键计算中需要计算的各类矩阵元表示为约化密度矩阵与轨道积分的张量收缩[49-52].利用共变与逆变轨道重叠积分的正交性质，行列式间矩阵元的计算可以应用Condon-Slater规则，极大地简化各类矩阵元的计算，降低计算标度.通过引进单占据轨道数的概念，采用一级单占据轨道数截断近似的VBSCF方法能计算多达22活性电子/22活性轨道的分子体系[74-77].这是当前国际上已被报道的价键计算活性空间的最大极限.

4 从头算价键理论计算软件

相比于分子轨道理论方法，由于理论方法的数学复杂性，价键理论从头算软件的开发难度相对较大，实际计算应用对计算资源要求相当高，应用范围相对较小.目前，国际上从头算价键理论软件非常稀少，特别是基于HLSP函数的价键理论计算软件.

TURTLE[78-79]是由van Lenthe等开发的价键计算程序包，该程序可以实现VBSCF、BOVB、BLW等方法的计算，并实现了基于价键波函数的分子几何构型优化.TURTLE程序已经嵌入GAMESS-UK软件，并且能够进行并行计算.

VB2000[80]是由李加波等开发的从头算价键程序包，该程序采用群代数算法，并且结合群函数理论，可以用于研究较大体系.该程序包已被GAMESS-US软件支持.

XMVB[81-82]程序是本团队开发的非正交轨道从头算价键程序.目前XMVB已经实现了本文介绍的所有价键计算方法.根据研究目的，用户可以非常灵活地定义价键轨道形式，如HAO、BDO、OEO等，并灵活确定用于计算的价键结构.此外，图形化工具XMVB-GUI为用户提供了方便友好的图形界面进行价键计算以及可视化计算结果.最新的XMVB 3.0版本能够处理高达22个电子/22轨道的活性空间，可以处理基函数数目大于1 000的分子体系.

以上3个计算软件可以采用HLSP函数构造多电子波函数，且价键轨道可以选用HAO形式，通常被认为是经典价键理论从头算软件.此外，下列计算软件也同样被认为是价键理论计算软件，但由于不是采用严格定域的HAO形式，或者体系多电子波函数不是采用HLSP函数形式，通常不被接受为经典价键理论软件.

Goddard等发展的GVB方法被誉为现代价键理论方法，其计算效率高，程序实现相对容易，目前国际上主要的大型通用量子化学软件如Gaussian和GAMESS等，都可以实现GVB方法计算.

Gerratt、Raimondi和Cooper发展了SCVB方法并实现程序化.目前，SCVB方法及其后续发展的方法如SCGVB[83]和CASVB[84]等,可以应用Molpro软件实现计算.

由Gallup开发的CRUNCH(Computational Resource for Understanding Chemistry)软件是基于表函数的价键计算软件[85]，它可以实现某些分子轨道理论方法的计算.

5 总结与展望

随着过去40年来取得的巨大进步，从头算价键理论的时代已经到来.从头算价键理论方法的优势包括两个方面：一方面，价键理论能够提供一种从头算水平上的量子化学计算工具，从概念性的角度来准确地研究化学键的本质.相比于分子轨道理论方法，由于采用了电子配对概念来构造体系的多电子波函数，价键理论在研究分子成键特征、化学反应过程等方面具有天然的优越性.另一方面，作为基于分子轨道的多参考波函数方法的补充，价键理论已经能够进行高级别的电子结构计算.在透热态的计算上，价键理论相比于分子轨道理论具有其独特的优势，这对于反应动力学的研究至关重要.相信随着价键理论计算速度和计算精度的不断提高，价键理论方法将越来越受到理论和实验化学家的重视，从而使其能够得到更加广泛的应用和发展.