基于DTW改进灰色关联算法的飞机着陆安全操作研究

齐凯 陈文瑛

【摘 要】飞行员在最后进近着陆阶段准确执行一系列操作，是飞机安全着陆的重要保证。首先，将最后飞行阶段分为200ft-50ft、50ft至接地两个阶段，研究了9项飞行状态参数的灰色接近关联度。其次，设计了一种DTW改进灰色接近关联算法，降低因飞行数据抽样造成的算法误差。研究表明，保持横侧和下降率的稳定是安全着陆的重要前提。俯仰角、空速归一化值、地速、油门杆位移、驾驶杆位移、脚蹬偏移量等参数在50ft-0ft阶段越接近于标准序列，着陆载荷越逼近1.3 g左右的理想着陆状态，飞机着陆安全性越高。

【关键词】飞行数据 ；重着陆 ；灰色关联分析；动态时间弯曲算法

中图分类号：V323 文献标识码：A 文章编号：1674-1722（2021）01-0079-04

★项目名称：民航安全能力建设项目“基于日常运行数据的不稳定进近研究及实时个性化应用”

飞机进近着陆阶段由于近地面气流紊乱，速度、高度变化范围大，操作程序复杂，已成为飞行事故和不安全事件的多发阶段。典型的不安全事件包括不稳定进近、重着陆、长着陆等[1]。对影响飞机着陆安全的相关飞行参数和飞行员操纵进行分析，对保障飞机着陆安全具有重要的意义。

飞行数据不仅可用于事后的飞行事故调查，还可以作为飞行操纵品质监控的重要参考。飞行数据往往存在记录噪声和偏差不确定性。灰色系统理论常用于处理部分信息已知的不确定性系统。通过对观测数据进行分析，可以找到因素间的数学关系并挖掘因素自身的变化规律。灰色系统理论是主要研究概率统计和模糊数学方法难以解决的贫信息、小样本的不确定性问题，依据信息覆盖原则，通过序列算子作用探索系统动力学规律[2]。尽管航空技术取得巨大进展，仍然无法消除复杂气象环境、驾驶员错误操纵等不确定性对飞行安全的严重威胁。因此，采用灰色关联度计算分析外部扰动或驾驶员操纵对飞行状态的影响，深入研究飞行参数间的关联性，能够为控制飞机着陆风险提供参考。

本文运用灰色关联分析方法，对飞机进近着陆过程中的若干飞行参数的影响因素进行分析，考虑飞行数据的时间序列特征，分析得到影响飞机着陆安全的关键影响参数。在此基础上，通过融合灰色系统理论和动态时间弯曲算法，降低飞行数据的采样帧率不同造成的计算偏差，从而进一步提高计算精度。

一、基于灰色接近关联度的影响参数分析

在飞机进近着陆阶段，飞机记录的各类参数偏差与进近程序、扰动风、飞行员操纵习惯等密切相关，具有显著的不确定性，即数据灰度较大，整体的飞行数据可以看作一个灰色系统。本文首先选用灰色接近关联方法进行典型进近着陆航段分析，以验证模型与方法的有效性；然后使用该方法找出在时间序列上对接地载荷影响较大的关键阶段参数。每个参数被分成200ft-50ft、50ft-0ft两个阶段后，分别分析两阶段参数间的关联序。由于灰色关联分析要求数据长度一致，在本节的分析中，须通过对高帧率的数据进行抽样，形成所有数据的统一长度。

（一）灰色接近关联分析

（二）灰色接近关联分析试验

根据实际航段的飞行数据，计算它们与标准模型的灰色接近关联序列并进行对比。本文先后选择地速、下降率、俯仰角、滚转角、接地空速与参考速度的差值、驾驶杆位移、油门杆位移、驾驶盘位移、脚蹬位移共9项飞行状态参数，对其在200ft-50ft、50ft-0ft这两个阶段的灰色接近关联度分别进行计算。本文将3360个航段均根据其重量建立相应的标准着陆模型，计算各阶段参数与标准着陆模型的关联度值。如下图1所示，左侧坐标轴表示各着陆载荷区间的航段数量N，右侧坐标轴表示关联度值e大小，两条折线分别表示两个阶段的关联度曲线，折线上的点为该区间所有航段的e的均值。由圖1可知，80%以上的航段集中分布在1.05g-1.35g区间内。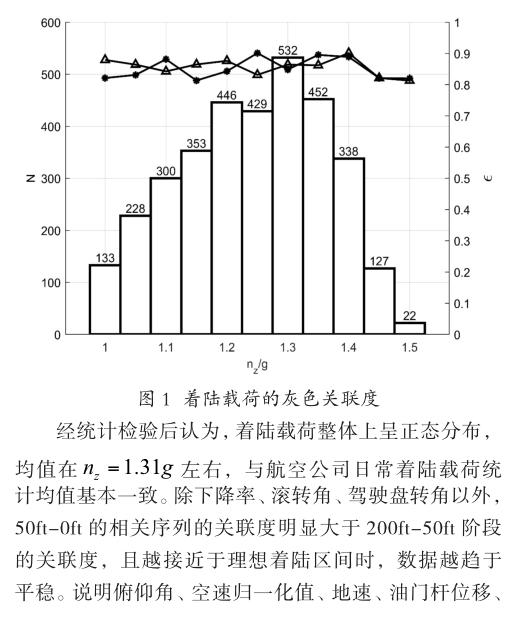

另一方面，针对下降率、滚转角、驾驶盘转角这3个参数，200ft-50ft的相关度和50ft-0ft的相关度差别不大。从进近着陆飞行过程来看，在跑道入口高度50 ft前必须保持稳定的下降率。因此，这一分析结果与飞行操纵是相符的。着陆前保持飞机横侧稳定性也是基本的飞行训练要求，若在50ft高度前不能保证横侧稳定性，则创造跑道入口条件更加困难。从本文选取的飞行航段样本来看，没有出现横侧不稳定的现象。

二、基于动态时间弯曲修正的灰色接近关联度分析

（一）动态时间弯曲DTW算法

针对时间序列数据，有多种距离度量方法。其中应用最广泛的是欧式距离算法和动态时间弯曲（Dynamic Time Warping， DTW）算法。前者是一种利用两组时间序列之间的欧式距离来度量他们的相似性。但是一般的时间序列中，需要比较相似性的两段时间序列可能并不相等。例如，在比较同一航班的两次飞行数据时，两次航班的飞行时间并不一致。其次，不同的时间序列可能仅仅存在时间轴上的平移。在这些情况下，使用传统的欧氏距离无法有效度量两个时间序列之间的相似性。相反，DTW方法引入序列对齐的思想，允许两个时间序列在不同时间戳处的数据进行比较。采用DTW方法，使序列中的点不再是一一对应关系，而是表现为一对一、一对多和多对一共存的多种映射，则可以扭曲时间轴使得序列之间总体的距离最小化。

当两组序列不等长时，基于DTW算法实现不同长度的时间序列之间相似程度的比较。传统DTW算法引入动态规划算法，导致时间复杂度高，计算成本较大。为解决计算成本问题，在DTW算法的路径寻找过程中引入A*算法，以加快算法的运行速度。A*算法是一种静态网络中求解最短路径的有效方法[5]。可将距离矩阵D作为寻路图，， i jd数值作为代价加入到代价函数的计量中，从而寻得由1，1d到， n md的最短距离，返回的路径距离即本算法计算得到的两序列间的相似程度。

（三） DTW改进灰色关联算法分析试验

最后进近着陆过程中，数据记录的俯仰角q与驾驶杆位移c d、滚转角f与驾驶盘转角Wd有密切联系。但记录的飞机姿态角频率为4 Hz，驾驶杆、盘的记录频率为8 Hz。且在截取数据进行分析的时候，同样的数据截获条件下，截获的数据长短可能有区别。以下首先进行灰色关联算法、DTW改进算法的性能比较。图2为选取的某一典型航段的4个参数记录时间序列。

针对上述4组飞行数据进行灰色关联分析，计算结果为：俯仰姿态角q和驾驶杆位c d的绝对关联度0.8954；俯仰姿态角q和驾驶盘位Wd的绝对关联度0.5372；驾驶杆位c d和横滚姿态角f的绝对关联度0.9007；横滚姿态角f和驾驶盘位Wd的绝对关联度0.5003。

通过DTW改进算法分析，进一步降低了由于统一序列长度而带来的算法误差，使得这种解耦性表现出更强的趋势。

以下仍选取归一化空速、地速、下降率、俯仰角、滚转角、驾驶杆、盘、脚蹬、油门杆位移，选取200ft-50ft和50ft-0ft两个阶段，分别将其与标准着陆航班的对应数据进行模型建立，分析其与标准序列在DTW改进算法下的相似程度，结果如圖3表示。

可以看出，经DTW改进算法的计算结果显示出与灰色关联算法类似的结论，且下降率、驾驶盘转角、滚转角在两个飞行阶段表示出更强的一致性。因此，飞行员须在最后进近阶段始终保持这3个参数的稳定性。就其他参数而言，进入跑道入口后的操作对垂直载荷具有更强的影响。

通过研究实际飞机进近与着陆阶段数据发现，在飞行过程中，如果飞机在200ft-50ft通过不断调整，最后50 ft按标准下滑，飞机也可以安全着陆，但如果最后50 ft对下降率和滚转角的保持、驾驶盘操作不得当，则重着陆发生的概率就会大大增加。

三、结语

本文首先研究了9项飞行状态参数在200ft-50ft、50 ft至接地的灰色接近关联度，得出的结论是俯仰角、空速归一化值、地速、油门杆位移、驾驶杆位移、脚蹬偏移量等参数在50ft-0ft阶段越接近于标准序列，着陆载荷越逼近1.3 g左右的理想着陆状态。着陆前保持横侧和下降率的稳定是安全着陆的重要前提。在此基础上，设计了基于动态时间弯曲修正的灰色接近关联算法，降低了因飞行数据抽样造成的算法误差，进一步强化了相关结论。上述结论与飞行操作实践完全符合。

参考文献：

[1]王冉， 高振兴. 基于飞行数据的民机着陆安全影响因素研究[J]. 交通信息与安全， 2019， 37（04）： 27-34.

[2]刘思峰， 杨英杰， 吴利丰等. 灰色系统理论及其应用.第8版[M]. 北京： 科学出版社， 2017.

[3]刘思峰， 蔡华， 杨英杰等. 灰色关联分析模型研究进展[J]. 系统工程理论与实践， 2013， 33（8）：2041-2046.

[4]韦增欣，陆莎. 非线性优化算法[M]. 北京：科学出版社，2015.

[5]Jiawei Han， MIcheline Kamber， Jian Pei. Data Mining， Concepts and Techniques[M]. New York： Wiley，2012.