Theoretical and Experimental Investigation of Driver Noncooperative-Game Steering Control Behavior

Xiaoxiang Na and David Cole

Abstract—This paper investigates two noncooperative-game strategies which may be used to represent a human driver’s steering control behavior in response to vehicle automated steering intervention. The first strategy, namely the Nash strategy is derived based on the assumption that a Nash equilibrium is reached in a noncooperative game of vehicle path-following control involving a driver and a vehicle automated steering controller. The second one, namely the Stackelberg strategy is derived based on the assumption that a Stackelberg equilibrium is reached in a similar context. A simulation study is performed to study the differences between the two proposed noncooperativegame strategies. An experiment using a fixed-base driving simulator is carried out to measure six test drivers’ steering behavior in response to vehicle automated steering intervention.The Nash strategy is then fitted to measured driver steering wheel angles following a model identification procedure. Control weight parameters involved in the Nash strategy are identified. It is found that the proposed Nash strategy with the identified control weights is capable of representing the trend of measured driver steering behavior and vehicle lateral responses. It is also found that the proposed Nash strategy is superior to the classic driver steering control strategy which has widely been used for modeling driver steering control over the past. A discussion on improving automated steering control using the gained knowledge of driver noncooperative-game steering control behavior was made.

I. INTRODUCTION

THE introduction of automated driving systems to modern vehicles brought marked improvement to driving safety.Meanwhile, this raised interesting questions of the influence of vehicle automation on drivers’ control behavior. Assessment of the performance of automated driving systems currently relies heavily on experimental approaches using test drivers. The drivers’ subjective feelings on the performance of automated driving systems are interpreted into engineering terms to advise design changes. A consequence is that the development of automated driving systems is time-consuming and expensive.Besides, new development in technology may expand vehicle performance envelope into a region where previous knowledge of the mapping from test driver’s subjective feelings to vehicle design changes becomes inapplicable [1]. Towards this end,mathematical models capable of representing human drivers’control behavior in response to the intervention of automated driving systems in are in demand. Such models are believed useful in supporting the development of automated driving systems in low-cost computer-aided design phases. However,an absence of thorough theoretical understanding of what control strategy a human driver may adopt to interact with automated driving systems is presently limiting the application of mathematical driver models in technology development.

Elsewhere in engineering, economics, and neuroscience,game theory has been widely used to model situations in which two or more individuals make decisions that influence one another’s welfare [2]. As a descendant of game theory,dynamic game theory specializes itself in dealing with circumstances where players make decisions repeatedly over time [3]. Dynamic games can be classified into noncooperative games and cooperative games, according to their mode of play [4]. In a noncooperative game, each player focuses on pursuing his/her individual interest while in a cooperative game, players arrive at a binding agreement of interest [5].The strategy that a game player adopts has predominant influence on his/her welfare. A strategy of a player is essentially a mapping of the states of the game to the player’s action [6]. The strategies of all players constitute a strategy set. An equilibrium is such a strategy set that every player has the belief that his/her strategy has reached an optimum in terms of maximizing his/her welfare. In other words, no player is willing to change his/her strategy unilaterally [7].Nash and Stackelberg are two typical equilibria observed in noncooperative games. A Nash equilibrium may emerge when each player chooses to develop his/her strategy by taking the others’ behavior into account, and all players take actions simultaneously. A Stackelberg equilibrium may emerge in games of the leader-follower form, where the leader player derives strategy by considering all the followers’ strategies while all the followers stick to their own optimal responses[8].

In a dynamic game, players may have different knowledge about the states of the game. The term “information pattern”was proposed by Başar and Olsder [3] to describe a player’s knowledge of the states of a game. Players who have openloop information pattern are defined to know only the initial states of a game. In contrast, players who have closed-loop information pattern can get access to intermediate states of a game. More detailed classification of the closed-loop information pattern, e.g., in terms of players’ measurability and memorization of game states are explained in [3].

A linear quadratic (LQ) game is a special case of a dynamic game. In a LQ game, the dynamic evolution of the game system is describable by a linear differential equation, and the players’ cost functions are describable by affine-quadratic terms [4]. Since a LQ game is analytically tractable and numerically solvable, it has been extensively used for modelling and solving dynamic game problems. Of particular note here is the work done by Braun et al. [9] who constructed a LQ game model to predict human players’ hand movements in a two-person rope- pulling game. High degree of agreement was achieved between model-predicted and experimentmeasured human players’ arm movements. This implies that human sensorimotor interaction may be modeled and represented in a dynamic game context.

The interaction between a human driver and an automated vehicle may also be understood from a dynamic game point of view: the driver and the automated driving controller are game players that make decisions and take actions in a repeated way, and their decisions are continuously influence by each other’s actions. Inspired by the work done by Braun et al. [9]and enlightened by the dynamic-game nature of driverautomation interaction, the authors of the present paper proposed a set of dynamic-game schemes in [10], aiming at modeling and representing human drivers’ steering interaction with an active front steering (AFS) system [11] in a pathfollowing scenario, where the AFS system is capable of making decision and applying steering control independently of the human driver. One scheme was derived by assuming that a Pareto equilibrium is reached when the driver and the AFS controller are playing a cooperative game in vehicle steering control. Such a scheme was investigated via simulation analysis in a recent publication by the authors [12].Another two schemes were derived based on the assumption that the driver interacts with the AFS in a noncooperative game context. Specifically, one involves driver adopting a steering control strategy that has a Nash equilibrium property while the other involves a Stackelberg equilibrium. It was not covered in [10] how the driver noncooperative-game steering control strategies can be validated via experiments.

The assumption that human drivers adopt noncooperativegame strategies to interact with vehicle automation was implied in some research on vehicle dynamics control.Tamaddoni et al. [13] reported a vehicle yaw stability control algorithm based on the assumption that the driver’s steering control and the vehicle controller’s yaw moment control can reach a Nash equilibrium. Dextreit and Kolmanovsky [14]reported a controller for energy management in hybrid vehicles based on the assumption that the driver’s speed control and the controller’s speed control can reach a Stackelberg equilibrium. Flad et. al [15] developed a steering torque assistance controller that seeks to reach a Nash equilibrium with the driver’s steering torque. Most recently, Ji et al. [16], [17] developed a noncooperative-game framework for designing driver-automation shared control, where the vehicle automation in [16] was implemented via an automated angle-overlay steering system, and later in [17] a torqueoverlay system. In all these studies, the effectiveness of the proposed vehicle controllers was tested via simulation and/or experiments. However, so far it has been an open question whether drivers in reality interact with vehicle automation by using some degree of noncooperative-game control strategy.

The present paper attempts to field the question through investigating whether human drivers may interact with an AFS system by adopting noncooperative-game steering control strategies. To achieve this goal, an extension to the authors’ previous work [10] from theoretic perspective is first carried out. This involves conducting a numerical study to explore the difference between a driver’s noncooperative Nash and his/her noncooperative Stackelberg steering control strategies. Another extension to [10] from experimental perspective is then carried out. This involves fitting the formula of driver noncooperative Nash strategy to realistic driver steering control behavior measured using a fix-base driving simulator. On this basis, a discussion on the improvement of vehicle automated steering according to the observed driver steering behavior is made.

The contribution of the paper may be summarized as follows. First, the significant difference in driver steering behavior between adopting Nash and Stackelberg strategies are revealed. Second, the validity of the proposed Nash steering strategy for representing human drivers’ realistic steering interaction with vehicle automated steering control is demonstrated. Third, detailed design improvement to existing automated steering control is suggested based on the gained knowledge of driver steering behavior in response to automated steering control. It is noteworthy that besides game theory, reinforcement learning is a powerful approach to dealing with noncooperative and distributed decision-making problems, especially when only partial information is available to some of the decision-making entities, e.g., [18][19]. A key reason that the game-theoretic approach is adopted in the present work is that it allows for a synthesis of linear quadratic representation of a mechanistic driver model and that of a dynamic game system. In such a circumstance,the mechanism of a human driver’s steering control can be explicitly described using model parameters, including driver prediction horizon, control horizon, control weights on target path tracking error, game-system convex iteration steps etc.On determining the values of these model parameters,quantitation of an individual driver’s driving skill and style can be conducted, such as the work reported in [20] and [21].In view of this, it is expected that penetrating insight into the underlying mechanism of driver-automation interaction may be achieved by using a game-theoretic driver modeling approach. On this basis, optimization and customization of present or future automated driving interface, e.g., shared control [22], and parallel driving [23] becomes a possibility.

The remainder of the paper is organized as follows. Section II delineates the theoretic schemes for studying noncooperative steering interaction between a human driver and a vehicle AFS controller. Section III formulates the derivation of a driver’s noncooperative Nash and Stackelberg steering strategies. A simulation study is carried out to explore their differences. Section IV describes an experiment for measuring human driver’s steering behavior in response to AFS control in a path-following scenario. Section V presents the outcomes of fitting the driver Nash steering control strategy to the measured data and illustrates the superiority of the Nash strategy over a classic steering strategy in representing driver steering behavior Section VI suggests possible design improvement of vehicle automated steering control by using the gained knowledge of human drivers’ noncooperative-game steering control behavior. Section VII draws conclusions and suggests future work.

II. DRIVER-AFS NONCOOPERATIVE GAME THEORETIC STEERING CONTROL SCHEMES

The two driver-AFS noncooperative game theoretic steering control schemes to be investigated are illustrated respectively in Figs. 1 and 2. The scheme shown in Fig. 1 is the driver-AFS Nash steering control scheme, in which the driver adopts a steering control strategy having the Nash equilibrium property. The one shown in Fig. 2 is the driver-AFS Stackelberg steering control scheme, in which the driver adopts a steering control strategy having the Stackelberg equilibrium property.

Fig. 1. Driver-AFS Nash steering control scheme.

Fig. 2. Driver-AFS Stackelberg steering control scheme.

A. Driver-AFS Nash Steering Control Scheme

In the driver-AFS Nash steering control scheme shown in Fig. 1, the AFS controller determines its steering angleδ2(k)at time step k using vehicle state x(k), AFS target path R2(k),and driver steering angle δ1(k). The AFS control law is obtained by minimizing cost function J2(k, x, R2, δ1, δ2) at time step k. Such a cost function concerns penalizing the difference between vehicle state x and AFS target R2(k). Both driver steering angle δ1and AFS angle δ2are involved because vehicle state x is subject to both of them. As a result,the AFS control law can be conceptually expressed as

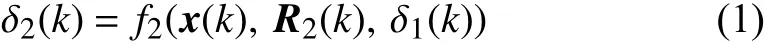
where f2( ) denotes the rule that maps x(k) , R2(k) and δ1(k) to the AFS steering angle δ2(k). The vehicle state x(k) is a vector composed of vehicle dynamic responses such as lateral velocity v(k) , lateral displacement y(k) and yaw rate ω(k).They can be measured using low-cost sensors or estimated using practical methods, e.g., those reviewed in [24]. The AFS target path R2(k) can be determined independently of the driver’s intention by using various onboard sensing hardware and software. The driver steering angle δ1(k) can be measured using low-cost sensors that have been equipped in most modern vehicles. In (1), δ1(k) is taken into account by the AFS system so that the AFS can compensate for undesirable driver steering behavior, which is possibly due to human error. The idea of compensating driver action in vehicle control was reported in several studies, e.g., by Anderson et al.[25] and Li et al. [26].

B. Driver-AFS Stackelberg Steering Control Scheme

III. DERIVATION OF DRIVER NASH AND STACKELBERG STEERING CONTROL STRATEGIES

In this section, derivation of a driver’s Nash and Stackelberg steering control strategies is presented. A simulation study is then carried out to explore their differences.

A. Vehicle Dynamics Model

The dynamics of a vehicle is represented using the linear time-invariant “bicycle” model, as described in [10]

B. AFS Control Law

The noncooperative model predictive control (MPC)approach is used to derive the analytical expressions of the AFS control law in this subsection. It will be used to derive the driver’s Nash and Stackelberg steering control strategies later.

Noncooperative MPC was proposed by Rawlings and Mayne [30] as a combination of noncooperative game theory and distributed MPC method. The distributed MPC method was developed first as a solution to industrial process control of large-scale systems. The core idea of distributed MPC involves decomposing a large-scale system into smaller subsystems, and deploying local controllers to control the subsystems. Hence, the communication between the local controllers has a major impact on the control performance.The noncooperative MPC approach is characterized by designing the communication between local controllers based on noncooperative game theory: each local controller views the others’ control actions as known disturbances and tries to compensate for their effects.

Rawlings and Mayne [30] explained that the communication can be alternatively designed based on cooperative game theory, leading to the cooperative MPC approach. The communication can also be removed to simplify the control problem, leading to the decentralized MPC approach.However, neither of them will be touched in this paper.

Continuing to follow Rawlings and Mayne [30], three steps are followed to derive the AFS control law through using the noncooperative MPC approach. First, the AFS controller’s prediction equation is established by iterating vehicle dynamics equation (4) for N2steps ahead. N2thus denotes the AFS controller’s prediction horizon. In other words, future vehicle dynamic responses are predicted based on vehicle model (4). During the process, both the AFS and the driver steering angles are kept unchanged over the prediction horizon N2. As a result, the AFS controller’s prediction equation can be obtained

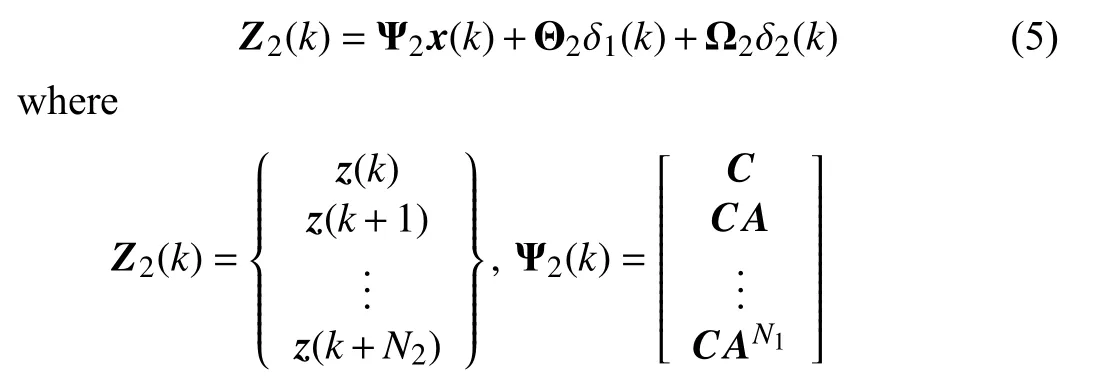
C. Driver Nash Steering Control Strategy

In this subsection, the driver Nash steering control strategy is derived using the noncooperative MPC approach [30].

D. Driver Stackelberg Steering Control Strategy

In the Stackelberg case, the driver is assumed to develop his or her prediction equation in a different way from the Nash case. Specifically, the driver substitutes the AFS control law(7) into his or her prediction equation (12) employed in the Nash case to generate a more sophisticated prediction equation (16)

It can be seen that (18) is a steering strategy minimizing driver cost function (13) subject to prediction equation (16).As (16) implies the driver’s consideration of AFS control law in his/her prediction, (18) is thereby a strategy that bears the Stackelberg equilibrium property in a leader-follower game[8], where the AFS acts as the follower who sticks to its control law (7) while the driver acts as the leader who keeps in mind what control law the AFS sticks to. Equation (18) can be then written as

E. Simulation Study

TABLE I DRIVER MODEL PARAMETERS USED FOR SIMULATION STUDY

Prior to the numerical simulation, stability of the closedloop driver-AFS Nash scheme (Fig. 1) and that of the Stackelberg scheme (Fig. 2) were analyzed using the procedure suggested by Rawlings and Mayne [30]. Under the Nash scheme, AFS control law (7) and driver Nash strategy(15) were injected into vehicle model (4) to generate the following closed-loop system:

Following the analysis made above, Cases A, B and C were simulated. Fig. 3(a) illustrates the results from Case A. The left subplot shows the driver’s straight-line target path (square marker), the AFS controller’s lane-change target path (cross marker), and the resultant vehicle lateral displacement (dashed line for driver Nash strategy; dotted line for driver Stackelberg strategy). The right subplot shows driver and AFS steering angles (dashed line for Nash; dotted for Stackelberg). In Case A, driver Nash strategy (15) results in larger steering angles than driver Stackelberg strategy (19). Meanwhile, the adoption of Nash strategy allows the driver to follow his or her straight-line target path more closely than that of Stackelberg strategy.

Fig. 3(b) shows the results from Case B, where the values of driver control weights are doubled from Case A. This allows the vehicle to follow the driver’s straight-line target path more closely compared to that shown in Case A. However, there is no significant change in driver and AFS angles from Case A.

Fig. 3(c) shows the results from Case C. The driver control weights are kept the same as those used in Case A, while the driver prediction horizon is reduced to 150 steps. In this case,the driver’s path-following performance declines significantly compared to that in Case A. It also can be seen that under the Stackelberg scheme, driver and AFS steering angles decrease significantly compared to that shown in Case A.

IV. DRIVING SIMULATOR EXPERIMENT

In this section, the experiment using a driving simulator for measuring human drivers’ steering behavior in response to AFS control law (7) is described.

A. Driving Simulator and Test Drivers

A fixed-base driving simulator developed in the Department of Engineering at the University of Cambridge using MATLAB Real-Time Workshop was used. A driver can apply control to the simulator vehicle model via steering wheel, accelerator pedal and brake pedal. A variety of studies on driver behavior has been conducted using this driving simulator, e.g., [36]. Six test drivers with an average driving experience of 4.8 years were employed. They were marked respectively as Test Drivers 1 to 6. Their details are provided in Table II.

B. AFS Lane Change Maneuver for Driver Steering Behavior Measurement

Fig. 3. Simulation results of vehicle lateral displacement and driver and AFS steering angles. Subplots (a), (b) and (c) respectively show results obtained under Cases A, B and C (as per Table I). Dashed: driver adopting Nash steering control strategy; dotted: driver adopting Stackelberg steering control strategy.

TABLE II TEST SUBJECT DETAILS

TABLE III AFS LANE CHANGE TARGET PATH PROFILES USED FOR EXPERIMENT (m)

In the experiment, an AFS system adopting control law (7)was programmed into the driving simulator. The simulator was set to run the linear time-invariant “bicycle” vehicle model (4) with a sample time Ts= 0.01 s at a constant longitudinal speed U = 20 m/s. The vehicle parameters used for the experiment are the same as those used for the numerical simulation in Section III. The AFS was then set to perform lane change maneuvers automatically at some point in the experiment. The lane change maneuvers mimic the collision avoidance actions that an AFS system may take following detecting an obstacle in front of the vehicle. Each test driver will be asked to apply steering action to keep the vehicle moving straight ahead. As a result, conflict over steering control will occur between driver and AFS.

1) AFS Target Paths

Six AFS lane change target paths of different profiles were used for the experiment, as shown in Table III. Three of them involve leftward lane change and the others involve rightward lane change. The dimensions were designed carefully to ensure that these lane change maneuvers could represent realistic crash avoidance path while maintain the vehicle model (4) to operate in a regime that would give linear behavior of a real vehicle.

2) AFS Controller Parameters

C. Experiment Track and Results

Following the trail for determining AFS control weights, the experiment was started. The six test drivers described in Table II were invited to drive the simulator vehicle and interact with the programmed AFS controller that carried out automatic lane change follow control law (7) to track its six target paths shown in Table III. Specifically, each test driver was asked to try his or her best to apply steering control to keep the vehicle travelling straight. As a result, conflict over steering control occurred between driver and AFS. Such conflict is likely to happen when there is an error in the AFS system, or when drivers thinks their target paths are morally more acceptable[35]. Test drivers’ steering angles in response to AFS control were measured by the driving simulator. It should be noted that in the experiment, test drivers were not informed the existence of AFS control but simply reminded that there might be some disturbance to their driving. They were neither given by the driving simulator any additional stimulus that may excite them to change their driving behavior. Once the AFS starts a lane change, the driver would only feel a change in steering wheel torque feedback, as what they would experience exactly in driving a real vehicle on road, due to the development of tire lateral force. In other words, test drivers were not intentionally guided to reach any equilibrium status.Instead, they were left by themselves to develop their own control in response to AFS intervention. Such a design bears the same nature as that employed by Braun et al. [9], who found that their human test subjects’ sensorimotor interaction in a rope-pulling game can be reproduced using the Nash equilibrium solution of a dynamic noncooperative game.

It can be imagined that if the AFS automatic lane change maneuvers were frequently imposed to a test driver over a short period, the driver may memorize the characteristics of the AFS control. As such memorization may change a driver’s steering behavior, it should be avoided. Therefore, several disturbance events were designed to impair a test driver’s memorization of the AFS automatic lane change control. The disturbance events are implemented by applying to the simulator vehicle 1) a step angle overlaid at its front wheels,2) an impulse angle at its front wheels, 3) a step lateral force at its center of gravity, and 4) an impulse lateral force at its center for gravity. These events were parameterized to excite vehicle lateral responses in different strength. The disturbance events and the AFS lane change maneuvers were triggered one by one in a random order along a straight experiment track, as shown in Fig. 4.

In the experiment, all the six test drivers’ steering angles and the vehicle’s lateral displacement were measured. Figs. 5 and 6 illustrate the measurements obtained under AFS lane change Path 4, as per Table III. The right subplot in Fig. 5 shows the steering angles applied by test Drivers 2 (solid), 3(dashed), 5 (dotted) and 6 (dash-dot), and corresponding AFS angles. The left subplot in Fig. 5 shows the profile of AFS lane change Path 4 (cross marker), that of driver straight-line target path (square marker), and the vehicle lateral displacements resulting from the interaction between test drivers and the AFS controller. Fig. 6 shows the results from Drivers 1 (solid) and 4 (dotted) in the same pattern. It can be seen that Drivers 2, 3, 5 and 6 (shown in Fig. 5) were inclined to apply larger steering angles to suppress AFS automatic lane change control, compared to Drivers 1 and 4 (show in Fig. 6).As a result, they did better at bringing the vehicle back to the driver’s straight-line target paths, compared to Drivers 1 and 4. In contrast, Drivers 1 and 4 tended to expand less steering effort to oppose AFS control, which caused the vehicle to continuously deviate from the driver’s straight-line target path. The difference in driver steering behavior between what was captured in Figs. 5 and 6 was not peculiar under AFS lane change Path 4, but universal among all the six AFS lane change paths. More details on test drivers’ steering angles were provided in [37]. With some prior knowledge of the driver model identification results (to be presented in Section V), the classification of the six test drivers’ steering behavior into two categories (according to Figs. 5 and 6) was found to agree with the distribution of the driver model identification errors. More details and discussions will be provided in Section V.

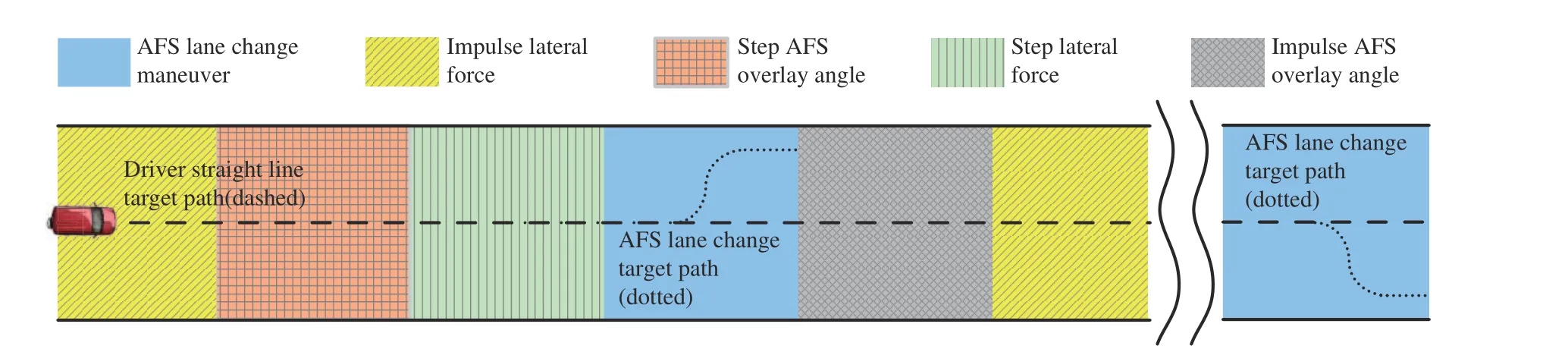
Fig. 4. Scheme of experiment track including AFS lane change maneuvers and disturbance events.

Fig. 5. Experiment results of vehicle lateral displacement and driver and AFS steering angles for test Drivers 2, 3, 5 and 6 along AFS lane change Path 4.Solid: test Driver 2, dashed: test Driver 3, dotted: test Driver 5, dash-dot: test Driver 6.

Fig. 6. Experiment results of vehicle lateral displacement and driver and AFS steering angles for test Drivers 1 and 4 along AFS lane change Path 4. Solid:test Driver 1, dotted: test Driver 4.

It should be noted that the AFS system is a time-critical system. In real vehicle applications, the real-time performance of the AFS system was guaranteed through both software and hardware optimization, such as that described in [11]. For the experiment concerned in this paper, the AFS system was programmed into the driving simulator, and its real-time performance was guaranteed by using MATLAB Real-Time Workshop. No violation of real-time execution was reported by the driving simulator throughout the experiment. This suggests that the AFS system used in this research maintained real-time performance successfully. This in turn allows test drivers to have sufficiently realistic feeling of driving in terms of interacting with the AFS system. It is also noted that all the six test drivers’ steering behavior were measured in a condition that the vehicle and AFS parameters were fixed. The authors acknowledged that a human driver’s steering behavior may change when these parameters change. However, since the authors’ aim is to investigate whether the proposed driver noncooperative-game steering control strategies is valid for representing measured driver steering behavior, the authors decided to fix vehicle and AFS parameters so as to minimize the complexity of the problem. Robustness of the proposed driver model to varying vehicle and AFS parameters is a topic of significance and will be examined in detail in future work.

V. DRIVER MODEL IDENTIFICATION

To investigate the validity of the proposed noncooperativegame steering control strategies for representing real driver steering behavior, a model identification task was carried out.This involves looking for a set of driver model parameters that allows a closest fit of the driver noncooperative steering control strategies to measured driver steering behavior.

In this section only the driver Nash steering control strategy is fitted to measured driver steering behavior while the driver Stackelberg strategy is not. This is because it would be more practical to assume that a driver is able to somehow recognize the AFS controller’s steering action, as required in the Nash strategy, rather than that the driver knows the AFS control law, as required in the Stackelberg strategy. However, one shall bear in mind that once a driver is imparted the AFS control law, by means of repeated training, it may become more acceptable to assume that a driver can adopt the Stackelberg strategy.

A. Identification Procedure

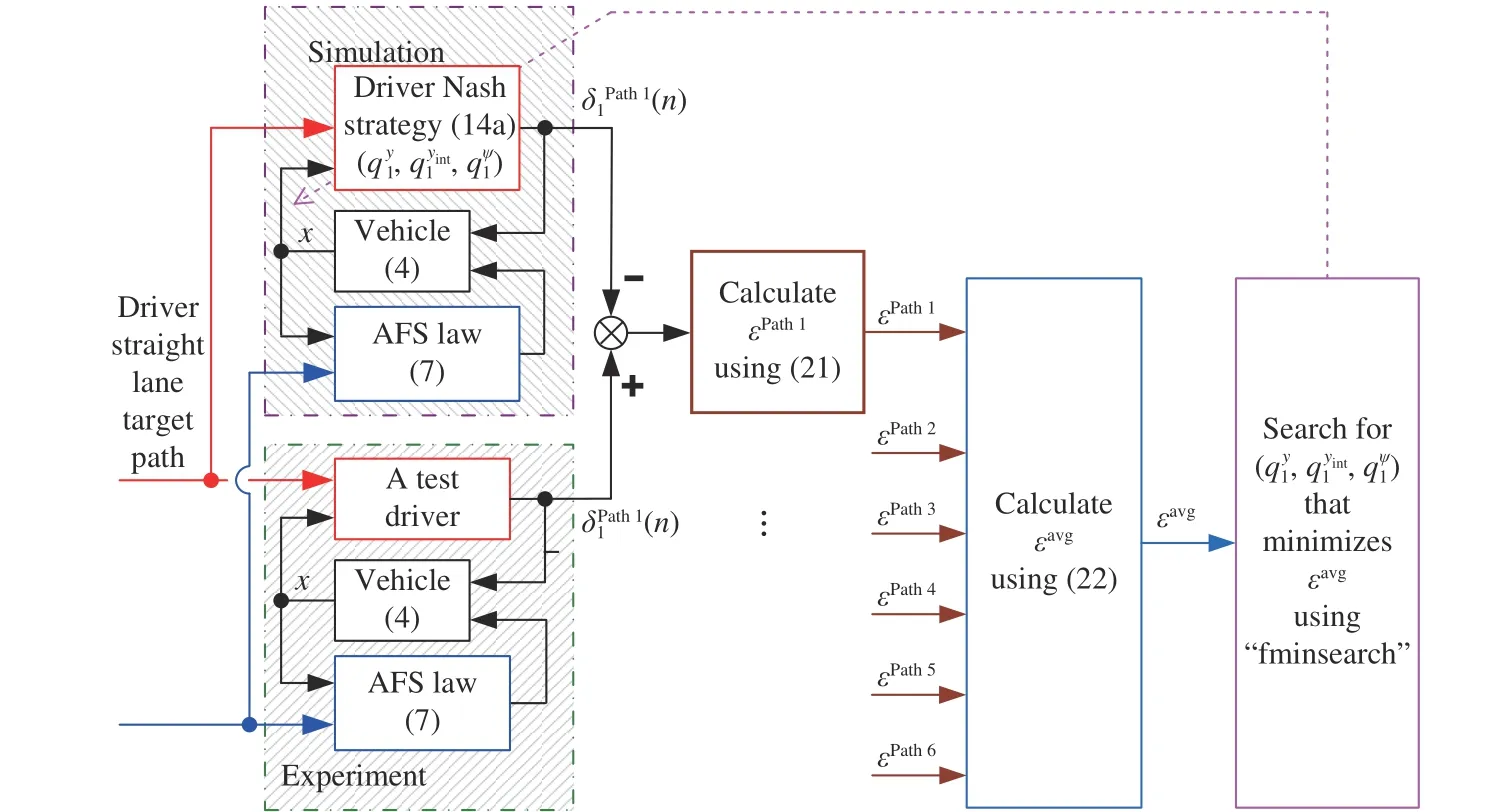
Fig. 7. Block diagram of identification procedure.

B. Identification Outcomes

Fig. 8. Test Driver 4’s simulation results from Nash strategy with identified weight set (, , ) (denoted using suffix “Sim”), and experiment results(denoted using suffix “Exp”) along AFS lane change Path 5.

Fig. 9. Test Driver 2’s simulation results from Nash strategy with identified weight set ?, , ) (denoted using suffix “Sim”), and experiment results(denoted using suffix “Exp”) along AFS lane change Path 5.

Based on all the six test drivers’ identification outcomes, a conclusive remark is made: the driver Nash steering control strategy (14a) is capable of representing the trend of each of all the six test drivers’ measured steering angles and that of the corresponding vehicle lateral response. However, (14a) is less capable of capturing the oscillation existing in the test drivers’ measured steering behavior.

C. Comparative Study between Driver Nash and Classic Steering Control Strategies

The subsection above shows the outcomes of fitting driver Nash steering control strategy (14a) to measured data. In order to better understand the superiority of (14a) in representing human drivers’ steering behavior, a comparator to (14a) was introduced. This comparator was named the driver’s classic steering control strategy. The term “classic” is used because the strategy was proposed first by MacAdam in 1981 [28], and was extensively validated in a number of separate studies,where the vehicle was controlled by a driver, without the presence of an automated system able to steer the vehicle independently of the driver.

Following the introduction of the driver classic strategy, an alternative driver-AFS steering control scheme which involves the driver adopting this classic strategy to interact with the AFS was established, as shown in Fig. 10. Such a scheme can be viewed as a modification to the driver-AFS Nash scheme(Fig. 1) by removing the driver’s accounting for the impact of the AFS control. Consequently, the driver’s prediction equation in the classic scheme can be written by reducing from (12) to

Fig. 10. Driver-AFS classic steering control scheme.

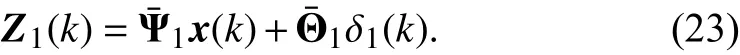
Fig. 11. Test Driver 4’s simulation results from “classic” strategy with identified weight set (qˆy1, qˆy1int, qˆψ1) (denoted using suffix “Sim”), and experiment results (denoted using suffix “Exp”) along AFS lane change Path 5. This figure is presented as a comparator to Fig. 8.

Fig. 12. Test Driver 2’s simulation results from “classic” strategy with identified weight set (qˆy1, qˆy1int, qˆψ1) (denoted using suffix “Sim”) and experiment results (denoted using suffix “Exp”) along AFS lane change Path 5. This figure is presented as a comparator to Fig. 9.

The driver classic steering strategy can be thereby expressed as other words, both strategies are able to represent the trend of measured driver steering behavior. But this is not the case for Test Driver 2. Driver 2’s simulated steering angles given by the classic strategy (Fig. 12) fails to capture the trend of his experimental measurement. This led to a continuing offset of 0.3 m between simulated and measured vehicle lateral displacement, as shown in Fig. 12. Such an offset did not appear when the Nash strategy was used (Fig. 9). This implies that the Nash strategy (14a) is superior to the classic strategy(22) in representing Test Driver 2’s steering behavior.

The observations made above are reflected in Fig. 13 which shows all six test driver’s identification errors εavgobtained from the Nash strategy (14a) (circle marker) and the classic strategy (24) (triangle marker). It can be seen that Driver 4’s εavgfrom the Nash strategy (14a) is very close to that from the classic strategy (24). Hence the two steering control strategies gave nearly identical simulated results in Driver 4’s case. In contrast, Driver 2’s εavgfrom the Nash strategy (14a) is much smaller than that from the classic strategy (24). Therefore, the Nash strategy is superior to the classic strategy in Driver 2’s case. It can be concluded from Fig. 13 that for Test Drivers 2,3, 5 and 6, the Nash strategy (14a) is superior to the classic one (24) in representing their measured steering behavior.However, for Test Drivers 1 and 4, the two strategies are of similar effect for representing measured driver steering behavior. This coincides with the note made early in Section III that Drivers 2, 3, 5 and 6 did better at bringing the vehicle back to the driver’s straight-line target paths, compared to Drivers 1 and 4.

VI. DISCUSSION

Fig. 13. Identification errors of all six test drivers.

Regarding the development of automated driving technology, human drivers’ reaction to the intervention of automation must always be considered. For liability and safety reasons, drivers are expected to retain their control of the vehicle [39]. This means that drivers should be offered the chance to override the automated driving technology. In view of this, the test drivers’ continuous increase of steering angles shown in Figs. 5 and 6 is not at all desirable. Specifically, if the AFS controller for some reason decides to keep on conducting lane change, the driver will have to keep on increasing steering angles to override the AFS. When the steering wheel reaches its limit position, the driver will have no more chance to override AFS. To this end, some improvement shall be made to the AFS control weights so as to avoid the driver’s continuous increase of steering angle.

Fig.14.Performance ofAFS path-followingcontrol when driver’ssteeringcontrolisin absence. Solid: AFScontrol with original weight set: qy2=0.6×10−3,qy2int=1.5×10−8and qψ2 =0;dotted:AFS controlwith improvedweightset:qy2=1.2×10−3andqy2int=qψ2 =0.

Fig. 15. Test Driver 4’s simulation results from Nash strategy (denoted using suffix “Sim”) and experiment results (denoted using suffix “Exp”) along AFS lane change Path 5, with improved AFS control weight set q y2=1.2×10−3 and q y2int=qψ2 =0 being in use.

Fig. 16. Test Driver 2’s simulation results from Nash strategy (denoted using suffix “Sim”) and experiment results (denoted using suffix “Exp”) along AFS lane change Path 5, with improved AFS control weight set q y2=1.2×10−3 and q y2int=qψ2 =0 being in use.

VII. CONCLUSION

This paper concerned theoretical modeling and experimental validation of noncooperative-game-theoretic driver steering control strategies. Two strategies, namely the Nash strategy and the Stackelberg strategy were derived based on the equilibrium solutions of a noncooperative game, where a human driver and an active front steering (AFS) controller hold different target paths and they compete for vehicle pathfollowing control. The driver Nash steering control strategy was fitted to measured human driver steering behavior, and the driver control weights involved in the Nash strategy were identified using a system identification procedure. The conclusions below were reached:

1) The Nash and Stackelberg Steering Control Strategies Represent Different Driver Steering Behaviors: The Nash strategy suggests that the driver determines his or her own steering angle by taking the AFS angle into account while the Stackelberg strategy suggests that the driver goes one step further by taking the AFS control law into account.

2) The Nash Strategy in Theory Results in More Aggressive Driver Steering Control: The steering angles given by the Nash strategy was found larger than those given by the Stackelberg strategy in a simulation study.

3) The Nash Strategy is Capable of Representing Measured Driver Steering Angles and Vehicle Lateral Responses:

Following adopting the driver control weights identified from measured human driver behavior, the Nash strategy was found capable of representing the trend of measured driver steering angles and vehicle lateral displacement for all the six test drivers used in the experiment.

4) The Nash Strategy is Superior to the Classic Strategy in Representing Human Driver Steering Interaction With AFS:

Compared to the driver Nash steering control strategy, the driver classic strategy was found less capable of capturing the trend of some test drivers’ measured steering behavior and resultant vehicle lateral responses. This suggests that the driver classic strategy in some case may be less suitable for modeling human drivers’ steering behavior in response to vehicle automation intervention; the Nash strategy could be a more suitable choice.

In the next step, neuromuscular dynamics of drivers’ arms will be modeled and incorporated into the driver Nash steering strategy for analysis. It is expected that the inclusion of driver arm neuromuscular dynamics can help the driver model capture the oscillation found in measured human driver steering angles.