A Multi-Layered Gravitational Search Algorithm for Function Optimization and Real-World Problems

Yirui Wang, Shangce Gao, Senior Member, IEEE, Mengchu Zhou, Fellow, IEEE, and Yang Yu

Abstract—A gravitational search algorithm (GSA) uses gravitational force among individuals to evolve population.Though GSA is an effective population-based algorithm, it exhibits low search performance and premature convergence. To ameliorate these issues, this work proposes a multi-layered GSA called MLGSA. Inspired by the two-layered structure of GSA,four layers consisting of population, iteration-best, personal-best and global-best layers are constructed. Hierarchical interactions among four layers are dynamically implemented in different search stages to greatly improve both exploration and exploitation abilities of population. Performance comparison between MLGSA and nine existing GSA variants on twenty-nine CEC2017 test functions with low, medium and high dimensions demonstrates that MLGSA is the most competitive one. It is also compared with four particle swarm optimization variants to verify its excellent performance. Moreover, the analysis of hierarchical interactions is discussed to illustrate the influence of a complete hierarchy on its performance. The relationship between its population diversity and fitness diversity is analyzed to clarify its search performance. Its computational complexity is given to show its efficiency. Finally, it is applied to twenty-two CEC2011 real-world optimization problems to show its practicality.

I. INTRODUCTION

NOWADAYS, there are various machine learning algorithms such as genetic algorithm (GA), particle swarm optimization (PSO), ant colony optimization (ACO)and differential evolution (DE) for solving diverse optimization problems, e.g., function optimization [1], [2],multi-objective optimization [3]-[6], dynamic optimization[7], [8], design optimization [9], [10], and combinatorial optimization [11], [12]. Also, for engineering problems such as milling manufacturing problems [13]-[15], optimization of vehicle components [16]-[18], mechanical problems [19], and wind engineering [20], optimization algorithms have shown their successful performance and potential. One of the most crucial investigations is to enhance their performance.Population-based algorithms continually evolve their populations to derive better results on optimization problems.Their population structures can influence the interactions among individuals to form complex networks [21]-[23].Adjusting population structures can be a kind of method to improve the performance of algorithms. Studies have proved that heterogeneous population structures can help individuals effectively evolve and reinforce their properties [24]-[26].

In optimization algorithms, the organization among individuals is formed via a population structure. A simple and common structure is panmictic [24]. In it, each individual interacts with other ones via random selection. Thus, frequent interactions among individuals implement quick information flow in the population. However, its population diversity cannot be maintained such that a premature convergence usually occurs. To address this issue, neighborhood structures are proposed to slowly propagate the information among individuals [26], [27]. They are designed to alleviate stagnation according to their fitness and spatial topologies.Generally, they are divided into two primary classes, i.e.,cellular and distributed ones [25], [28]. In a cellular structure,all the individuals are arranged in a grid and each individual only communicates with others in its neighborhood. These neighborhoods may be partially overlapped. This mechanism leads to a slow information flow from each individual to its neighborhood, and decreases the risk of premature convergence [26]. In [28], cellular GAs are introduced to show the smooth diffusion of solutions. In [29], [30], cellular PSOs improve their search ability in various dynamic environments. In [31], different neighborhood shapes and grid shapes of the cellular structure are investigated for a quantuminspired PSO. In [32], four different DEs use the cellular structure to enhance their performance. In [33], the direction of information flow the cellular structure provides is applied to the mutation operation of DE. In a distributed structure, the whole population is divided into several subpopulations.Individuals in each subpopulation independently evolve while the information among subpopulations is propagated by a migration strategy. Formally, each subpopulation searches its own specific region and a migration strategy shares effective information among different subpopulations. During the migration, one or more individuals in one subpopulation move into the other subpopulations via a migration strategy. The migration among subpopulations occurs in a given time. Since the distributed structure constructs several subpopulations,their exploration ranges are improved. Meanwhile, the migration among them further consolidates their population diversity. By this means, individual’s search ability can be reinforced. In [34]-[36], various multi-swarm PSOs are proposed for continuous and dynamic optimization. In [37], an invasion-based migration strategy is added into a distributed DE where the communication among individuals only occurs in real-connected subpopulations. In [38], two migration strategies containing target individual-based migration and representative individual-based migration are used to improve a distributed DE. More distributed DEs or other algorithms can be referred in the literature [26].

As a specific distributed structure, the hierarchy integrates several either cellular structures or distributed ones by a hierarchical framework, which can effectively share information among different structures [39]. It often possesses several distinctive layers where individuals accomplish more efficient evolution and diverse cooperation among them. The interactions among layers combine their heterogeneity and homogeneity in different structures. According to its characteristics, a hierarchical structure has been applied to various algorithms such as PSO [40], DE [24] and GA [41].Besides these neighborhood structures, other structures with such attributes as small world [42] and scale-freeness [24], [43]have been introduced. The theoretical analyses of population structures conclude that a specific topology influences the interactions among individuals and finally decides the performance of algorithms [44]-[46].

Gravitational search algorithm (GSA) inspired by the concept of gravity is a promising algorithm for optimization problems [47]. It uses the gravitational force to attract individuals. Since individuals have different masses and positions, the gravitational force can generate the accelerations and velocities on them. At present, a number of improved operators have been proposed to improve its performance. A disruption operator is introduced to influence the gravitational force of an individual with the highest mass on other ones [48]. A mutation operator enhances its population diversity by adjusting the velocities of individuals[49]. Chaotic operators implement a chaotic local search for it[50]. Crossover ones improve its local search ability [51]. An escape one makes individuals far away from their group return to the group according to their escape velocities [52]. A niching selection one is introduced into GSA where individuals are generated by a nearest neighbor scheme [53].Other operators such as black hole and kepler inspired from astronomy show their effectiveness on improving GSA [54],[55]. These operators effectively enhance its search performance. Besides operators, various GSA variants have been designed to address different optimization problems. An opposition-based GSA which combines current and opposite positions to explore solutions is proposed to resolve a power system problem [56]. For binary-valued problems, a binary GSA which only considers values 0 and 1 in each dimension is designed [57]. A discrete GSA considering a search space as a triangular hypercube and adopting a triple-value encoding scheme is used to solve a graph planarization problem [58].For a multi-objective optimization problem, a non-dominated sorting GSA using a non-dominated sorting algorithm and an external archive to move individuals and providing several elite solutions is introduced [49]. In addition, inspired by quantum theory, a quantum-based GSA enhances its population diversity and performance [59]. Furthermore, GSA has been successfully applied to numerous engineering problems such as power systems [60], pattern recognition[61], control [62], mechanical manufacture [63], industry fields [64] and structural optimization [65], [66], and exhibits its huge optimization potential in solving different kinds of problems.

Although GSA can solve various problems, its search ability is limited when it encounters complex problems with various local optima. In GSA, the K best individuals as a Kbestmodel play a crucial role in attracting all ones. They guide the worse individuals to move towards them. However, this model also brings about several disadvantages. Firstly, the computational time of GSA is high because the number of the K best individuals changes slowly [67]. This Kbestmodel needs to compute numerous information among individuals. Secondly,this Kbestmodel cannot maintain the diversity of the K best individuals [68], [69]. In other words, it is difficult for them to escape from local optima owing to no other mechanisms.Thirdly, in the late search process, the number of the K best individuals is few such that GSA has the low exploitation ability and slow convergence [70], [71]. To improve thisKbestmodel, the values of Kbesthave been calculated by chaotic systems [72], fuzzy systems [73] and mathematical functions[74]-[77] instead of its linear decrease. As mentioned above, a suitable population structure is beneficial for strengthening the interactions among individuals such that its performance is improved. PSO has been used to combine with GSA [78].Both combination is co-evolutionary and heterogeneous. A global best individual is introduced to provide an extra force for all ones. Afterwards, this method is further improved via adaptive coefficients [79]. It enhances the exploitation ability and alleviates the premature convergence. A hierarchical structure shows the effective control for the K best individuals[71]. Besides an original Kbestmodel, neighborhood structures are used to revise its components. A locally informed kneighborhood structure enables each individual to interact with its k neighbors according to a wheel topology [67]. This method decreases the computational complexity and prevents the stagnation. In [70], a dynamic neighborhood structure randomly divides an entire population into several nonoverlapping local neighborhoods. In each local neighborhood,individuals interact with each other.

To fully utilize the information generated by the interactions among individuals, this work proposes a multi-layered GSA called MLGSA to enhance its search performance by constructing a hierarchical population structure. It has four layers, i.e., population, iteration-best, personal-best and global-best ones. Three kinds of hierarchical interactions among four layers effectively guide the search of individuals and enhance their exploration and exploitation abilities. To evaluate its performance, its parameter sensitivity is firstly analyzed to determine the best setting. Then, nine GSA variants and four PSO variants are used to compare with it on twenty-nine CEC2017 test functions. Experimental results verify that the hierarchical structure and interactions enhance its performance, showing that it is the most competitive GSA variant. In addition, the effectiveness of its complete hierarchy is demonstrated via the hierarchical interaction analysis. Its population diversity is analyzed to show its influence on fitness diversity. Its computational complexity is analyzed to illustrate its efficiency. Finally, its practicality is demonstrated on twenty-two CEC2011 real-world optimization problems.

The novelty of this paper is that we reinforce the hierarchy of GSA according to its original two-layered structure to boost its search ability. Hierarchical interactions among four layers effectively guide the population. To be specific, the personalbest layer directs the iteration-best layer that guides the population layer, and the global-best layer leads the population layer. Meanwhile, sigmoid and reverse sigmoid functions are innovatively used in hierarchical interactions to enhance the exploration and exploitation ability of population.These two functions divide a search process into three stages,i.e., exploration, transition and exploitation stages. Thus, the hierarchical interactions among four layers dynamically change in different stages. More precisely, there are two kinds of hierarchical interactions among population, iteration-best and personal-best layers in an exploration stage. Three kinds of hierarchical interactions among four layers are completely implemented in a transition stage. In an exploitation stage,only the interaction between the global-best layer and population layer is executed. Based on this novel mechanism,a number of best individuals of GSA are effectively guided by the personal-best layer in an exploration stage and the population quickly converges by the global-best layer in an exploitation stage. Finally, the algorithm’s performance is significantly reinforced by its hierarchical structure and interactions.

The motivation of this paper is to construct the population structure to improve the performance of GSA. As a population-based algorithm, GSA uses the interactions among individuals to evolve. However, its interactive mechanism is simple such that individual’s search abilities are limited. To address it, the interactions among individuals should be refined via a sophisticated way. After we sufficiently research and analyze the characteristics of GSA, a hierarchy can be implemented to further effectively guide individuals. Different from those improved operators and newly added approach, the population structure directly changes the interactions among individuals to influence their search behaviors. It depends on the intrinsic attribute of one algorithm. Thus, a suitable population structure is able to strengthen individual’s search abilities [26], [39]. According to this principle, we apply the population structure to GSA in order to enhance its search performance.

The contributions of this paper can be summarized as follows: 1) A four-layered hierarchy is proposed from the perspective of a population structure. Hierarchical interactions among four layers effectively guide the population in different stages so as to reinforce the proposed algorithm’s exploration and exploitation abilities. They are analyzed to demonstrate the integrality and effectiveness of the proposed hierarchy.2) Population diversity and fitness diversity of the proposed algorithm are discussed to understand its search behavior. Its computational complexity is analyzed, which is not increased by the proposed hierarchical structure and interactions, thus implying its efficiency in solving optimization problems.3) The proposed algorithm is compared with nine GSA variants and four PSO variants, and proved to be the most competitive.

The rest of this paper is organized as follows. Section II gives a brief introduction to the basic GSA. Section III describes its issues and presents the proposed MLGSA.Section IV carries out its parameter sensitivity analysis and performance comparison with nine GSA variants and four PSO variants. Section V discusses the hierarchical interactions, population diversity, computational complexity and real-world optimization problems. Section VI gives conclusions and future research directions.

II. BASIC GSA

GSA inspired by the law of gravity is a population-based optimization algorithm. The gravitational force among particles determines their movement direction. The higher mass a particle has, the larger gravitational force on other particles it generates. This mechanism conducts the communication among particles and guides those with low masses to move towards ones with high masses according to their gravitational force. During this process, the position and velocity of each particle continually change to finally achieve an integrated balance among particles.

During function optimization, GSA considers each particle to be an individual. The interactions among individuals are realized by their gravitational force. Each individual’s position indicates a candidate solution in a function landscape, and its mass is represented by its fitness, i.e., a function’s value. A good individual should have a high mass, which can be a potentially good leader to attract other ones to move towards better positions. Therefore, individuals can find a global optimal solution according to their gravitational force with iterations.

III. MULTI-LAYERED GSA

A. Issues of GSA

Although GSA can seek for optimal solutions for optimization problems, its search ability is restricted by its original mechanism, thereby leading to local optima frequently [47], [50], [64]. This phenomenon manifests that GSA is likely to experience the premature convergence. The reason is that individuals depend on their gravitational force to frequently interact and evolve, but their gravitational force cannot guarantee that they are not trapped into local optima or can escape from the stagnation. Therefore, there should be some strategies assisting the gravitational force among individuals. Besides a premature convergence situation, GSA faces another issue which is low exploration and exploitation abilities. A good exploration process can locate a promising region where an optimal solution exists in the entire search space. Subsequently, a good exploitation process can finally find this optimal solution. Nevertheless, the exploration ability of GSA is insufficient in the initial search phase such that its low exploitation ability makes it difficult to find a global optimal solution in the late search phase. Due to this fact,local optima are generally derived. Consequently, a good trade-off between exploration and exploitation abilities should be made in order to enhance its search ability.

In GSA, movements of individuals are implemented via the integrated gravitational force that the K best individuals offer.To be specific, the K best individuals actively attract all the individuals to move towards them. This mechanism can promote the interactions among individuals, and the K best individuals play a vital part in leading them. However, theK best individuals can also accelerate the premature convergence of population once they are trapped into local optima, and without any capacity to prevent or address this circumstance.Thus, it is insufficient for enhancing the K best individuals only by using the gravitational force among them.Additionally, the K value gradually decreases with time,implying that the K best individual’s capacities to guide all the individuals are weakened such that the exploitation ability of GSA is lower and lower in the late search process.Meanwhile, it is more difficult for them to help the population escape from local optima. Therefore, it is considerably necessary to strengthen the exploitation ability of GSA in the late search phase so as to not only accelerate the convergence speed but also avoid suffering from the premature convergence. To address the above issues, a multi-layered GSA (MLGSA) is proposed to significantly enhance the performance of GSA.

B. Proposed MLGSA

From the viewpoint of population structure, a hierarchy requires us to divide individuals into different layers. Each layer has individuals with the same attribute. The interactions among layers implement the communication and evolution among individuals [26], [40]. This kind of hierarchical population structure can exert the difference among layers to effectively guide individuals. In GSA, a hierarchy is suitable for the population because the basic GSA has actually established a simple two-layered hierarchy where the K best individuals manage the whole individuals. This structure has also been successfully applied to resolve diverse optimization problems [60], [80], [81]. However, this current two-layered population structure is too oversimplified to usually obtain global optima according to previously mentioned reasons.

1) Hierarchical Structure: MLGSA contains four distinctive layers: population layer, iteration-best layer, personal-best layer and global-best layer. The personal-best layer guides the iteration-best layer that controls the population layer. Besides,the global-best layer also manages the population layer. This four-layered hierarchy not only effectively promotes theK best individuals but also consolidates the exploration and exploitation abilities of the algorithm such that individuals can acquire a better guided direction to overcome the premature convergence. Based on this structure, a hierarchical management is accomplished. Inspired by the two-layered structure of GSA, personal-best and global-best layers are established. To be specific, personal-best layer provides guide for iteration-best layer, and global-best layer controls population layer. Thus, a four-layered hierarchical structure is formed. Four layers in MLGSA are elaborated as follows:

a) Population layer: All the individuals in the population are placed at this layer. The evolution and position distribution of individuals at this layer are implemented by the other layers. In other words, the other layers bestow an effective guideline upon the population layer. Thus, this layer primarily offers an entire search space to the population, and all the individuals can continually evolve.

b) Iteration-best layer: This layer aims to determine several iteration-best individuals in current population to guide the population layer. To guarantee the fundamental mechanism of GSA, the K best individuals are selected at this layer. That is to say, the iteration-best layer attracts the population layer to achieve basic GSA functions. Individuals at the population layer evolve with the help of the gravitational force that the iteration-best layer offers. In addition, the number of individuals at this layer dynamically changes due to the linear decline of K with time.

c) Personal-best layer: In order to enhance the exploration ability and prevent the K best individuals from trapping into local optima, this layer is newly established. Each individual has its own best historical position during the search process,which is called its personal best individual. This individual represents its best solution so far. Since the K best individuals evolving according to their gravitational force only are prone to suffer from the premature convergence, we should find other individuals helping them avoid or escape from local optima. Thus, at this layer, K personal best individuals corresponding to the K best ones are selected to provide more information for further guiding the iteration-best layer. Each personal best individual at this layer specially guides its corresponding one at the iteration-best layer. Similarly, the number of individuals at this layer changes according to those at the iteration-best layer.

d) Global-best layer: The purpose of this layer is to improve the exploitation ability, assist the population in getting rid of local optima, and accelerate the convergence of population.Since the exploitation ability of GSA is too low to effectively resolve the stagnation of population in its late search process,a global best individual is adopted at this layer to further lead the population layer. A global best individual indicates the best solution in the population so far. Hence, the influence of this layer on the population layer is that all the individuals move towards the global best one such that a better solution may be found.

Fig. 1 intuitively shows the hierarchy of MLGSA. In this figure, there are N individuals at the population layer, i.e.,X1,X2,..., and XN, and the K best ones at the iteration-best layer, i.e., I1,I2,..., and IK. The iteration-best layer attracts the population layer according to the gravitational force.Meanwhile, there are K personal best individuals at the personal-best layer, i.e., P1,P2,..., and PK, and a global best one gbat the global-best layer. The personal-best layer guides the iteration-best layer by individuals one to one, e.g.,P1guides I1, and PKguides IK. The global-best layer further leads the population layer. That is to say, a global best individual gboffers an extra evolutionary direction to the population. According to this hierarchical structure,individuals are purposely classified into four layers to achieve effective evolution.

Fig. 1. Illustrative structure of MLGSA.

2) Hierarchical Interactions: In MLGSA, there are three types of hierarchical interactions among four layers. To be specific, the first is the interaction between iteration-best layer and population layer, which uses the gravitational force to evolve individuals. The second is the interaction between personal-best layer and iteration-best layer, which adopts the personal best individuals to guide their current best ones. The last is the interaction between global-best layer and population layer, which employs a global best individual to direct the population. The relationship among three hierarchical interactions determines the ultimate evolution of individuals such that the performance of algorithm is enhanced. These three hierarchical interactions are described as follows:

a) Interaction between iteration-best layer and population layer: The K best individuals at the iteration-best layer attract all the individuals at the population layer by the gravitational force among them. Thus, the interaction between these two layers abides by the GSA principle. More precisely, the gravitational force is generated according to masses of individuals, distance among them and gravitational constant.Nevertheless, the gravitational force calculated by the basic GSA is relatively low in the early search phase due to an inefficient gravitational constant, which causes a low exploration process [47], [82]. Thus, we define a new gravitational constant to replace the previous one. A sigmoid function is used, i.e.,

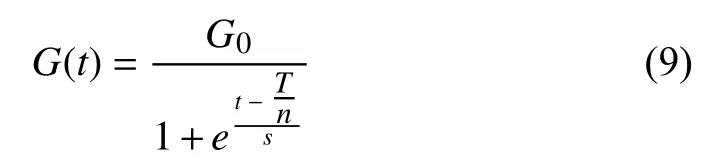
where n is a threshold to indicate the centre point of a curve according to the maximum iteration count T , and s determines the steepness of curve. Obviously different from the previous gravitational constant, this new one can prolong the exploration period of population such that the interaction between these two layers is more effective as shown in Fig. 2(a), to be discussed later. Based on this improved gravitational constant, the gravitational force among individuals maintains a relatively large value in the early search process to enhance their exploration abilities. After the influence of gravitational force, individuals at the population layer generate new velocities to change their positions according to their accelerations.

b) Interaction between personal-best layer and iterationbest layer: In order to effectively guide the K best individuals,Kpersonal best ones are used. Each personal best individual at the personal-best layer specifically directs its corresponding one at the iteration-best layer. This kind of one-to-one control can further reinforce the property of individuals according to their historical best positions. The explicit implementation is given as follows:

where Piindicates the i-th personal best individual corresponding to the i-th best one at the iteration-best layer and βiis the updated velocity of the i-th best individual.rand(-1,1)denotes a uniform random number in the interval(-1,1). To ensure the synchronism of interactions among personal-best layer, iteration-best layer and population layer,the effect among them should simultaneously occur. Thus, a sigmoid function is used to decide the interaction period between personal-best layer and iteration-best layer so as to enable it to be identical with that between iteration-best layer and population layer. It means that the K best individuals are further guided by their personal best ones. Additionally, it should be noticed that the influence of personal best individuals on their current corresponding ones is determined by a random number in the interval (-1,1). This random number aims to let the K best individuals move towards their personal best ones if it is a positive value or make them far away from their personal best ones if it is a negative value.Therefore, it can guarantee that the K best individuals are effectively guided and not completely trapped into local optima. Based on the interaction between these two layers, the Kbest individuals obtain extra velocities to change their positions.

c) Interaction between global-best layer and population layer: A global best individual manages the population to enhance the exploitation ability of population and accelerate the convergence of algorithm in the late search phase. The concrete control is implemented as follows:

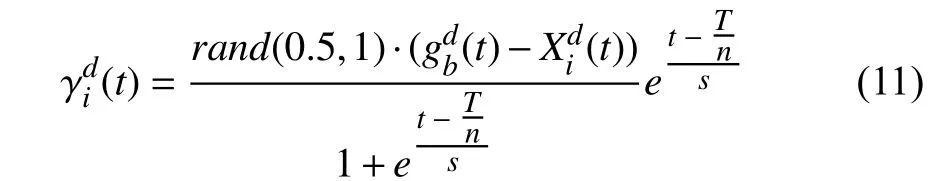
where gbindicates the global best individual and γiis the updated velocity of guided individual Xi. As stated above, the interaction between these two layers is to primarily enhance the performance of population in the late search process.Thus, a reverse sigmoid function is used to distinguish the interaction period among the other layers. More specifically,the interactions among personal-best layer, iteration-best layer and population layer focus on an exploration process, whereas the interaction between global-best layer and population layer pays attention to an exploitation process. A random number in the interval (0.5,1) ensures that the population can quickly move towards the global best individual. Accordingly, the population can acquire additional velocities to further enhance its position by the interaction between these two layers.

According to three kinds of hierarchical interactions among four layers, individuals finally evolve with their updated velocities as follows:

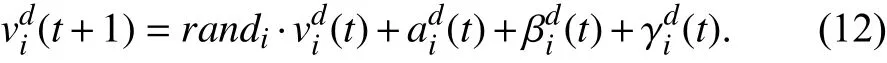
New velocities facilitate the effective movement of individuals such that the population can perform better during the search process.

C. Characteristics Analysis of MLGSA

Basic GSA uses an exponential gravitational constant G to generate the gravitational force among individuals. These gravitational force can quickly decrease due to the exponential attenuation of G. Thus, individuals cannot acquire enough exploration ability to traverse the search space. In other words, the exploration period and extent of population are obviously insufficient such that the premature convergence occurs. However, in MLGSA, a sigmoid G can effectively alleviate this issue. Between iteration-best layer and population layer, G maintains a relatively large value in a long term to enhance the gravitational force so as to expand the search range and period of individuals. It strengthens the interaction between these two layers to significantly improve the exploration ability of population. Fig. 2(a) shows the curves of exponential and sigmoid G where

G0=100, α=20, n=3/2, s=100, and T =3000. From this figure, it can be observed that the exponential G quickly declines in the early search process whereas the sigmoid one keeps an invariably large value in the early search process and begins to quickly decline in the late search process. This sigmoid G effectively extends the exploration period of population to implement more sufficient search in a search space. Therefore, the exploration ability of population is significantly enhanced between iteration-best layer and population layer.

Since the K best individuals lack an effective guidance at the iteration-best layer, the personal-best layer is constructed to effectively manage them. Between personal-best layer and iteration-best layer, a sigmoid function determines their interaction period and extent. It should be noted that this sigmoid function is the same as that between iteration-best layer and population layer in order to guarantee the simultaneous interactions among three layers. In other words,the exploration ability of population is further reinforced by the interaction between personal-best layer and iteration-best layer. Furthermore, this kind of extra exploration can prevent the K best individuals from trapping into local optima or help them escape from local optima by a random value in the interval (-1,1). That is to say, personal best individuals may not only attract their corresponding best ones but also exclude them to expand their search range. Thus, the interaction between personal-best layer and iteration-best layer effectively guides the K best individuals to further strengthen the exploration ability of population.

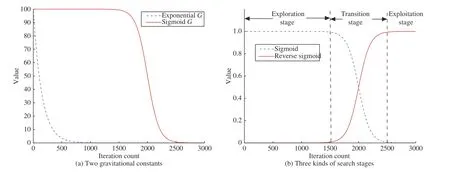
Fig. 2. The curves of new gravitational constant G, sigmoid and reverse sigmoid functions in MLGSA.

In the late search process, the exploitation ability of population is vital for its convergence. Since the exploration period of population is prolonged to improve its exploration ability, its exploitation ability needs to be further intensified in a short term. The interaction between global-best layer and population layer ameliorates this issue. It not only enhances the exploitation ability of population but also accelerates its convergence. A reverse sigmoid function differentiates the exploitation period of population from its exploration period.To be specific, there are distinctive periods between exploration and exploitation processes. A sigmoid function among personal-best, iteration-best and population layers decides the exploration period of population, whereas a reverse sigmoid function between global-best layer and population layer compensates for the exploitation period of population. Moreover, a random value in the interval(0.5,1)further accelerates the convergence of population.Consequently, the interaction between global-best layer and population layer enhances the exploitation ability of population to speed up its convergence and alleviate the premature convergence.

Fig. 2(b) shows the curves of sigmoid and reverse sigmoid functions used in MLGSA. From it, we can see that two functions have completely opposite characteristics. When the sigmoid function maintains a large value in the early search period, the reverse sigmoid one keeps a small value. It means that the exploration of population plays a crucial role whereas its exploitation is not implemented in the early search process.More specifically, the interactions among personal-best,iteration-best and population layers are only achieved to enhance the exploration ability of population. Thus, we can regard this stage as a complete exploration stage. When the sigmoid function begins to decline, the reverse sigmoid one begins to ascend. It implies that the exploration ability of population gradually decreases whereas its exploitation ability increases. At the same time, the interactions among four layers are accomplished to establish a transition between exploration and exploitation stages. In this transition stage, the population possesses both a gradually decreasing exploration ability and a progressively increasing exploitation ability.When the sigmoid function becomes a small value in the late search period, the reverse sigmoid one has a large value. That is to say, the interaction between global-best layer and population layer is carried out to enhance the exploitation ability of population and accelerate its convergence. As a result, this stage can be treated as a complete exploitation stage. According to the hierarchical interactions among four layers, MLGSA actually has three definite search stages, i.e.,complete exploration stage, transition stage and complete exploitation stage. In these three stages, MLGSA exerts different influence on the evolution of population.

MLGSA alleviates several disadvantages of GSA as follows: 1) The exponential gravitational constant in GSA declines quickly, leading to an insufficient exploration of population. MLGSA adopts a sigmoid gravitational constant to greatly enhance the exploration period and range of population. 2) In the hierarchical structure, the personal-best layer effectively guides the K best individuals. It not only prevents the K best individuals from trapping into the stagnation but also helps them jump out of local optima. 3) In the late search process, GSA has a low exploitation ability and slow convergence due to its considerably small exponential gravitational constant and number of K best individuals.MLGSA uses the global-best layer to further guide the population. It not only improves the exploitation ability of population but also speeds up the convergence. 4) MLGSA uses sigmoid and reverse sigmoid functions to construct three kinds of search stages where different hierarchical interactions are executed. However, the search process of GSA is monotonic decrease. MLGSA has a more complex and flexible search mechanism such that its search performance is significant.

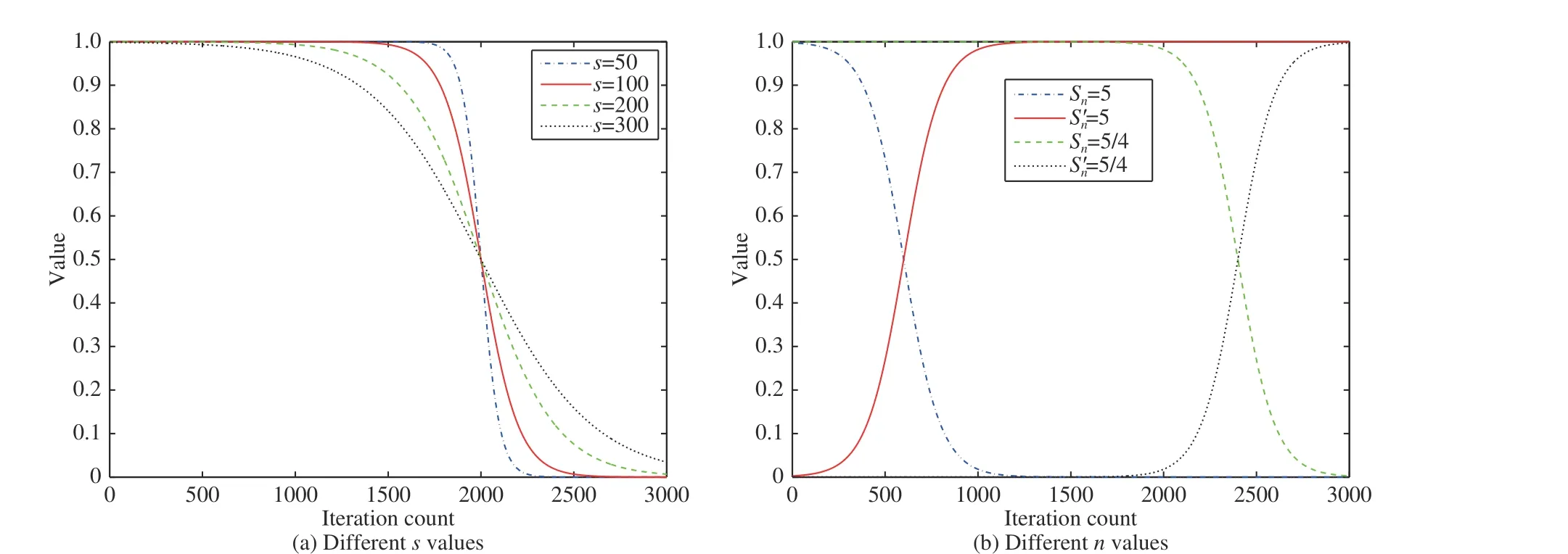
Fig. 3. The curves of sigmoid function with different s and n values in MLGSA.

IV. EXPERIMENTS

A. Experimental Setup

To evaluate the performance of MLGSA, twenty-nine CEC2017 test functions (F1－F29) are adopted [83]. These test functions are all used to ensure the accuracy and dependability of experimental results such that final analyses and conclusions are fair and solid. They provide diverse landscapes for algorithms to test their search performance. F1－F2 are unimodal. F3－F9 are multimodal. F10－F19 are hybrid.F20－F29 are composition. These functions have shifted and rotated characteristics, and distinctive optimal values. Hence it is complex and challenging for algorithms to address all of them well. In the following experiments, they are used as a test suite to measure the performance of algorithms.

In all experiments, the search range of a function is[-100,100]Dwhere D is the dimension of a function. The maximum number of function evaluations (NFEs) is 1 0000D.The population size N=100. Parameter settings of comparative algorithms are used according to their references.Each algorithm is independently run 30 times on each function to obtain its optimization errors which represent the error values between the optimal solutions found by the algorithm and the known global optimum. Statistical results of optimization errors are obtained by the Wilcoxon rank-sum test [84] at a significant level α=0.05 to show the difference between two algorithms. w/t/l presents the number of times that a target algorithm wins, ties and loses its peer,respectively. All experiments are carried out by a MATLAB software on a PC with 3.30 GHz Intel(R) Core(TM) i5 CPU and 8 GB RAM.

B. Parameter Sensitivity Analysis

We firstly investigate parameter s to determine the steepness of a sigmoid curve. n is set to be 3/2 to guarantee that the population has sufficient exploration and exploitation.sis set to be 50, 100, 150, 200, 250 and 300 to reveal the influence of the steepness of a curve on the performance of MLGSA. The experiment is conducted on twenty-nine CEC2017 test functions with 30 dimensions.

In order to determine the best s value, Table I givesw/t/l where MLGSA with s=100 is a target algorithm. According to statistical results, we can find that the number of winners is more than that of losers between s=100 and other values, and its winning number increases with s. It illustrates that a low steepness of a curve decreases the performance of MLGSA and a high one is proper for the algorithm. However, a higher steepness such as s=50 is also not the most suitable for the algorithm. This is because a low steepness of a sigmoid function can lead to low hierarchical interactions among four layers. For instance, in Fig. 3(a), before t=(2/3)T, population should have a strong exploration ability. Thereafter, the exploration ability of population should quickly descend so as to highlight its exploitation ability. For a low steepness of a sigmoid function, the hierarchical interactions among four layers cause a fact that the exploration ability of population decreases whereas its exploitation ability increases before t=(2/3)T. Subsequently, they descend and ascend so slowly that both abilities interfere with each other in the search process. This circumstance is incompatible with our expectation. Thus, the hierarchical interaction is weakened. In addition, a higher steepness may excessively reinforce the hierarchical interaction such that the performance of algorithm is inferior. Therefore, s=100 is the best value according to Table I.

After determining the steepness of our sigmoid function, its operative period needs to be studied. That is to say, the exploration and exploitation periods of population are investigated to guarantee effective hierarchical interactions among four layers. In this experiment, the parameters=100 is used. n is set to be 5/4,4/3,3/2,2,3,4 and 5 to indicate that the curve descends late, medially and early.

The statistical results in Table II demonstrate that MLGSA with n=3/2 outperforms that with other values. With the increase of n values from 2 to 5, the winning number ofMLGSA with n=3/2 is more and more. It suggests that the earlier the curve descends, the worse performance of algorithm. This is because a large n value leads to a short exploration period and a long exploitation one, which is contrary to our purpose. This kind of large n values are adverse to the hierarchical interaction. Thus, a small n value is suitable for the algorithm. However, a smaller n value such as 4/3 or 5/4 causes the inferior performance in comparison to n=3/2. It may be caused by too long exploration and too short exploitation periods, respectively, which is also harmful to the hierarchical interaction. Based on these experiments, the best parameters values of a sigmoid function, i.e., s=100 and n=3/2, are determined to achieve the most effective hierarchical interactions among four layers in MLGSA.

TABLE I WILCOXON RANK-SUM RESULTSOF OPTIMIZATION ERRORS OBT AINEDBY MLGSA BETWEEN PARAMETERs=100AND OTHER VALUESONTWENTY-NINE CEC2017 TEST FUNCTIONS WITH 30 DIMENSIONS

TABLE II n=3/2 WILCOXON RANK-SUM RESULTS OF OPTIMIZATION ERRORS OBTAINED BY MLGSA BETWEEN PARAMETER AND OTHER VALUES ON TWENTY-NINE CEC2017 TEST FUNCTIONS WITH 30 DIMENSIONS

C. Comparison Among Various GSAs

Nine GSA variants are used to compare with MLGSA. Four well-known GSAs consisting of GSA [47], gbest-guided GSA(GGSA) [79], modified GSA (MGSA) [85] and the combination of PSO and GSA (PSOGSA) [78] and five stateof-the-art GSAs including multiple chaos embedded GSA(CGSA-M) [86], improved GSA (IGSA) [82], dynamic neighborhood learning-based GSA (DNLGSA) [70],hierarchical GSA (HGSA) [71] and GSA with chaotic neural oscillators (GSA-CNO) [87] are used as the peers of MLGSA.GGSA adopts the best solution to additionally update all the individuals in order to enhance its exploitation ability. MGSA uses the global and local optimal solutions to modify the velocity update of individuals. PSOGSA is a hybrid algorithm which combines the exploration ability of GSA with the exploitation ability of PSO. CGSA-M uses a memory to adaptively select the best chaotic map to implement its chaotic local search. IGSA self-adaptively adjusts its gravitational constant and applies a modified chaotic local search so as to improve its exploitation ability. DNLGSA uses dynamically local neighborhoods to replace the original Kbestmodel and employs an adaptive mutation strategy to revise the global optimum in order to better balance its exploration and exploitation abilities. HGSA has a hierarchical structure to control the interactions among individuals. GSA-CNO employs chaotic neural oscillators to tune its gravitational constant.

The comparison among these algorithms is done on twentynine CEC2017 test functions with 10, 30 and 50 dimensions,which represent low, medium and high dimensions,respectively. Their statistical results are shown in Table III.

TABLE III WILCOXON RANK-SUM RESULTS OF OPTIMIZATION ERRORS BETWEEN MLGSA AND NINE GSA VARIANTS ON TWENTY-NINE CEC2017 TEST FUNCTIONS WITH 10, 30 AND 50 DIMENSIONS

w/t/l in D=10 of Table III shows that MLGSA significantly outperforms its competitors on many functions.To be specific, its winning number of times is 23, 19, 24, 21,24, 20, 24, 17 and 23 out of 29 over its nine peers,respectively. w/t/l in D=30 of Table III exhibits that the number of times MLGSA significantly outperforming its peers is 28, 26, 24, 23, 28, 16, 25, 16 and 18 out of 29,respectively. Compared with the 10 dimension cases, MLGSA performs better on functions with medium dimensions than those with low dimensions according to the comparison between MLGSA and the others. w/t/l in D=50 of Table III displays that the number of times MLGSA wins the others is 27, 25, 25, 22, 27, 12, 27, 18 and 19 out of 29, respectively.Except for IGSA, HGSA and GSA-CNO, MLGSA significantly outperforms GSA, GGSA, CGSA-M, MGSA,PSOGSA and DNLGSA on functions with high dimensions. It is similar for the performance of MLGSA between medium and high dimensions according to their w/t/l. Nevertheless,IGSA enhances its performance with the increase of dimensions such that the number of times that MLGSA outperforms it decreases. Despite IGSA reinforces its search ability on high dimension, MLGSA is competitive in terms of its w/t/l. Additionally, IGSA needs a considerably higher computational complexity in contrast to MLGSA. The computational complexity regarding them is discussed in Section V. HGSA and GSA-CNO are better than MLGSA on some functions, but the overall performance of MLGSA is more prominent. Thus, we can conclude from Table III that MLGSA executes an effective search process by its hierarchy on functions with different dimensions.

D. Comparison Among Various PSOs

MLGSA has shown its superiority against GSA variants. To further verify its performance, four PSO variants are adopted.Global PSO (GPSO) [88] is a PSO with the inertia weight.Orthogonal learning PSO (OLPSO) [89] uses an orthogonal learning strategy to guide individuals toward promising directions. Genetic learning PSO (GLPSO) [90] hybridizes PSO with the genetic evolution to improve its search ability.Competitive swarm optimizer (CSO) [91] introduces a pairwise competition mechanism to update individuals. These four algorithms are compared with MLGSA on twenty-nine CEC2017 test functions with 30 dimensions. Their parameter settings are used according to [88]-[91], respectively.

According to w/t/l in Table IV , MLGSA significantly outperforms GPSO, OLPSO, GLPSO and CSO on 20, 25, 19 and 21 out of 29 functions, respectively. Although MLGSA adopts personal best and global best individuals similar to PSO, its search performance is better than these four outstanding PSO variants due to its effective hierarchical structure and interactions.

TABLE IV WILCOXON RANK-SUM RESULTS OF OPTIMIZATION ERRORS BETWEEN MLGSA AND FOUR PSO VARIANTS ON TWENTY-NINE CEC2017 TEST FUNCTIONS WITH 30 DIMENSIONS

V. DISCUSSIONS

A. Analysis of Hierarchical Interactions

Since MLGSA has four layers, the hierarchical interactions among them should be further investigated to disclose the influence of hierarchy on the evolution of population. Thus,MLGSA is compared with its four variants, including a completely hierarchical GSA with an original gravitational constant (MLGSA-OG), a basic GSA with a sigmoid gravitational constant (GSA-SG), a partially hierarchical GSA consisting of iteration-best layer, population layer and globalbest layer (PHGSA1), and another partially hierarchical GSA composed of personal-best layer, iteration-best layer and population layer (PHGSA2). The comparison among them is conducted on twenty-nine CEC2017 test functions with 30 dimensions. Table V shows the Wilcoxon rank-sum results between MLGSA and its variants.

w/t/l in Table V shows the difference of performance between MLGSA and its variants where the winning number of functions by MLGSA in comparison with MLGSA-OG,GSA-SG, PHGSA1 and PHGSA2 is 23, 21, 12 and 8,respectively. The comparison between MLGSA and MLGSAOG clarifies that a sigmoid gravitational constant is significantly superior to an exponential one, suggesting that the interaction between iteration-best layer and population layer is able to achieve better exploration ability of population. The comparison between MLGSA and GSA-SG indicates that a hierarchical structure effectively guides the population to improve the performance of algorithm. The comparison between MLGSA and PHGSA1 elucidates that the personal-best layer can effectively guide the K best individuals to enhance their exploration abilities and alleviate premature convergence cases. The comparison between MLGSA and PHGSA2 shows that the global-best layer can enhance the exploitation ability of population. However, thenumber of times that MLGSA outperforms PHGSA2 is not large, implying that the current global-best layer is not sufficiently effective for improving the performance of algorithm on many functions. In other words, a revision regarding the global-best layer is worth further studying so as to strengthen the exploitation ability of population in the future work. According to these comparisons, we can conclude that a complete four-layered hierarchy effectively improves the exploration and exploitation abilities of population and thus reinforces the performance of GSA.

TABLE V WILCOXON RANK-SUM RESULTS OF OPTIMIZATION ERRORS OBTAINED BY MLGSA, MLGSA-OG, GSA-SG, PHGSA1 AND PHGSA2 ON TWENTY-NINE CEC2017 TEST FUNCTIONS WITH 30 DIMENSIONS

B. Analysis of Population Diversity

To analyze the diversity of MLGSA, we define two indices,i.e., population diversity ( PD) and fitness diversity ( FD) as follows:

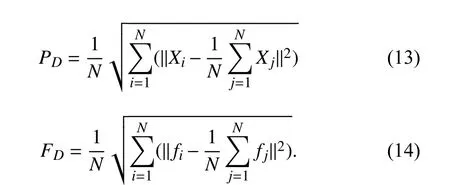
They describe the standard deviations of population and its fitness, respectively. Four kinds of functions are used as examples: 1) an unimodal function F2; 2) a multimodal function F3; 3) a hybrid function F10; and 4) a composition function F24. PDand FDof MLGSA are measured on them with 10, 30 and 50 dimensions. NFEs is 300 000 and each function is optimized for 30 times.

Figs. 4 and 5 show average PDand FDvalues. From them,we can observe that the curves of average PDare similar to those of average FDon four functions with 10, 30 and 50 dimensions. It reflects that average PDinfluences averageFDin MLGSA. When it declines, so does average FD. When it is large, so is average FD. This is because a large PDindicates the notable difference among individuals such that their fitness are significantly different. Next, we can find that average PDand FDgradually decrease in 10 dimensions whereas keep large values in 30 and 50 dimensions except for F2. This is because MLGSA obtains approximately global optimal solutions on four functions with low dimensions such that the population achieves effective convergence, resulting in the decrease of PDand FD. For functions with medium and high dimensions, since MLGSA does not obtain approximately global optimal solutions, its PDand FDremain large. However, there is an exception on F2 where the curves of average PDand FDdecline in three kinds of dimensions.Especially, they have a similar performance in 10 and 30 dimensions. This is because F2 is a simple unimodal function and MLGSA can effectively obtain the global optimal solution on it with low and medium dimensions. According to Figs. 4 and 5, we can conclude that MLGSA can obtain small PDand FDon functions with low dimensions whereas remain sizable on complex functions with medium and high dimensions,suggesting that its population diversity remains large for finding optimal solutions when the dimensions of functions increase.

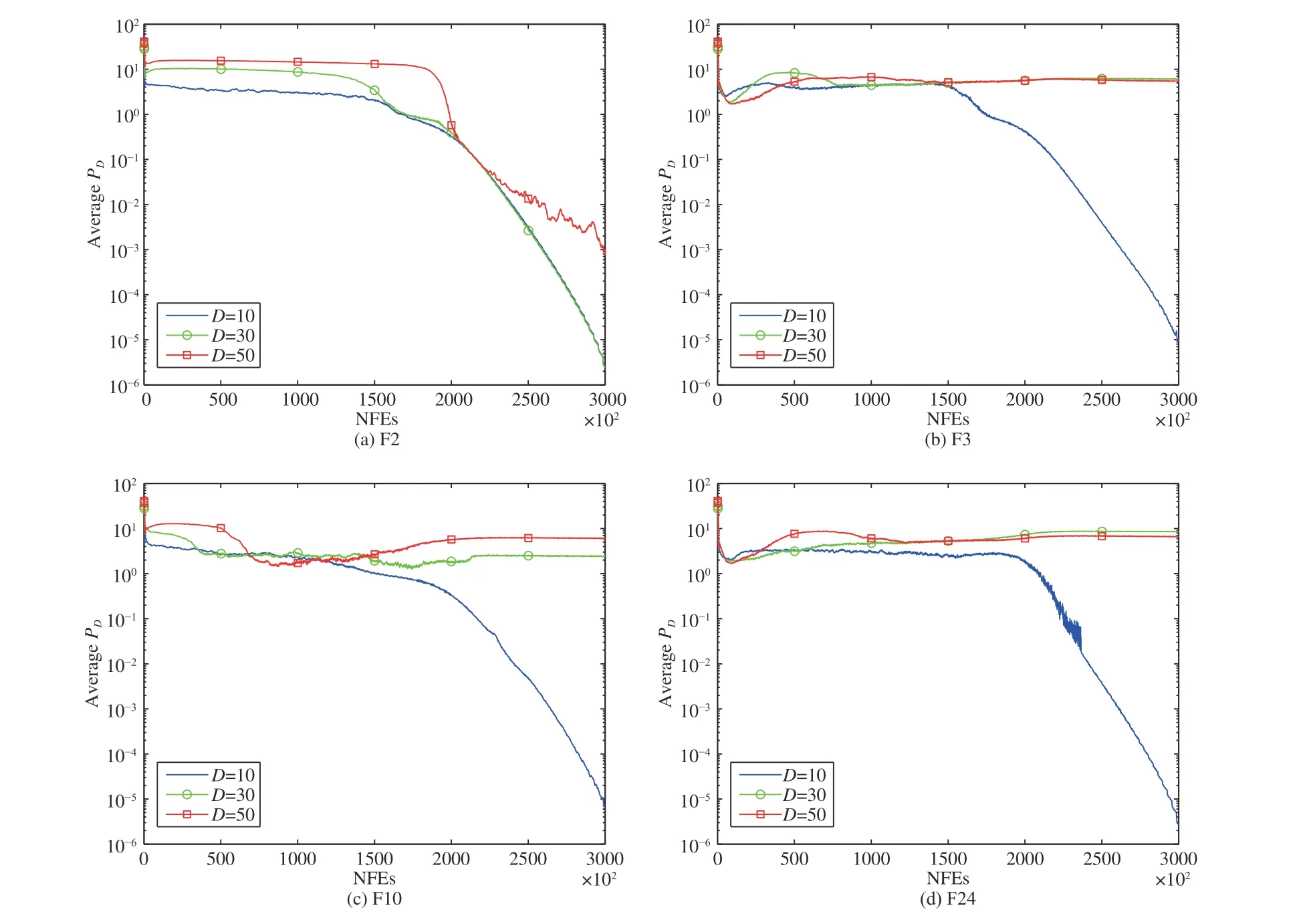
Fig. 4. The curves of population diversity of MLGSA on four kinds of functions with 10, 30, and 50 dimensions.

Fig. 5. The curves of fitness diversity of MLGSA on four kinds of functions with 10, 30, and 50 dimensions.

C. Analysis of Computational Complexity

MLGSA has shown its effectiveness on optimizing functions. Next, its efficiency is investigated in terms of computational complexity. Population size N is considered in its analysis. The complexity of its primary procedures is given as follows:

1) The initialization process needs 3 O(N)+O(1);

2) The operation of overstepping boundary in the worst case requires 3 O(N);

3) Evaluating the fitness of population takes O (N);

4) Updating the personal-best layer in the worst case consumes 2 O(N);

5) Updating the global-best layer in the worst case needs O(N+1);

6) Calculating the mass of population costs 4 O(N);

7) Updating the iteration-best layer in the worst case requires O (N2+K);

8) The interaction between iteration-best layer and population layer takes 3 O(KN);

9) The interaction between personal-best layer and iterationbest layer consumes 2 O(K);

10) The interaction between global-best layer and population layer needs O (N);

11) Updating the population layer costs 2 O(N).

Thus, the overall computational complexity of MLGSA is O(N2).

Besides MLGSA, the computational complexity of GSA,GGSA, CGSA-M, MGSA, PSOGSA, IGSA, DNLGSA,HGSA and GSA-CNO is calculated as well. Their computational complexity in the worst case is O(N2), O(N2),O(N2), O(N2), O(N2) , O(N4), O(N2/k), O(N2) and O(N2),respectively. For DNLGSA, since it uses a distributed structure to reduce its computational complexity, its number of local neighborhoods k must be considered. Except for DNLGSA and IGSA, we can find that MLGSA has the same computational complexity O(N2) as other seven GSAs,suggesting a hierarchy does not increase the computational expense of algorithm. In other words, MLGSA is an efficient algorithm. Although DNLGSA has the best computational complexity, its search performance is worse than MLGSA.Compared with IGSA, the computational complexity of MLGSA is obviously smaller. That is to say, although IGSA enhances its performance on functions with high dimensions,it needs to spend more time in adjusting its gravitational constant to find a better solution. Its efficiency is far inferior to MLGSA, and MLGSA is competitive with it on functions with high dimensions.

To give the stricter analysis of computational complexity,the method in CEC2017 literature [83] is used. Table VI shows the computational complexity of ten GSA variants on function F17 with 30 dimensions. T0is the computing time of the following test program:

TABLE VI COMPUTATIONAL COMPLEXITY OF TEN GSA VARIANTS

According to Table VI , DNLGSA has the smallestT�2 whereas IGSA has the greatest one. Except for them, MLGSA has a slightly smaller T�2than other seven GSA variants. These results demonstrate the above theoretical analysis, illustrating that DNLGSA is the fastest and IGSA is the slowest.Compared with other GSA variants, MLGSA has an effective and efficient search mechanism owing to its hierarchical structure and interactions among its four layers.

D. Real-World Optimization Problems

To validate the practicality of MLGSA, twenty-two CEC2011 real-world optimization problems are evaluated.Their description is shown in Table VII and specific information can be referred to [92]. Table VIII displays statistical results of optimal solutions obtained by ten GSA variants.

From Table VIII, MLGSA is significantly better than GSA,PSOGSA, MGSA, GGSA, CGSA-M, IGSA, DNLGSA,HGSA and GSA-CNO on 15, 14, 14, 12, 15, 16, 17, 8 and 10 out of 22 problems, respectively. HGSA and GSA-CNO are competitive with MLGSA. Compared with functions, realworld optimization problems are more complex and diverse.However, among ten GSA variants, MLGSA performs the best on several problems, suggesting its high practicality.

TABLE VII TWENTY-TWO CEC2011 REAL-WORLD OPTIMIZATION PROBLEMS

TABLE VIII WILCOXON RANK-SUM RESULTS OF OPTIMAL SOLUTIONS BETWEEN MLGSA AND NINE GGA VARIANTS ON TWENTY-TWO CEC2011 REAL-WORLD OPTIMIZATION PROBLEMS

VI. CONCLUSIONS

This paper presents a multi-layered gravitational search algorithm (MLGSA) that has population layer, iteration-best layer, personal-best layer and global-best layer. Among the layers, three kinds of hierarchical interactions effectively enhance exploration and exploitation abilities of its population. Its parameter analysis is conducted to determine its best parameter setting. The performance comparison between it and various GSAs verifies its superior search performance on most of twenty-nine tested functions with low, medium and high dimensions, which implies that it is the most competitive GSA variant. It is also compared with four PSO variants to show its good performance. Hierarchical interactions are analyzed to show the effectiveness of a complete four-layered hierarchy. The relationship between population diversity and fitness diversity on functions with different dimensions is discussed to show its search behavior.Its computational complexity is analyzed to reveal its competitive efficiency. Finally, its practicality is verified on twenty-two real-world optimization problems.

A hierarchy has shown its promising characteristics for refining the performance of GSA. In the future work, several issues are worth further studying: 1) The global-best layer needs to be improved to more effectively guide the population. 2) More complex hierarchical structures such as five or more layers could be designed to purposely control the interactions among individuals. 3) Besides a hierarchy, other population structures should be considered to combine with GSA to implement better attraction among individuals. 4) The current hierarchy of MLGSA based on the original structure of GSA is only suitable for GSA. A universal hierarchical structure should be devised to integrate into other heuristic algorithms, e.g., [93]-[95], to enhance their performance.