An Overview of Calibration Technology of Industrial Robots

Zhibin Li, Shuai Li, Senior Member, IEEE, and Xin Luo, Senior Member, IEEE

Abstract—With the continuous improvement of automation,industrial robots have become an indispensable part of automated production lines. They widely used in a number of industrial production activities, such as spraying, welding, handling, etc.,and have a great role in these sectors. Recently, the robotic technology is developing towards high precision, high intelligence.Robot calibration technology has a great significance to improve the accuracy of robot. However, it has much work to be done in the identification of robot parameters. The parameter identification work of existing serial and parallel robots is introduced. On the one hand, it summarizes the methods for parameter calibration and discusses their advantages and disadvantages. On the other hand, the application of parameter identification is introduced. This overview has a great reference value for robot manufacturers to choose proper identification method, points further research areas for researchers. Finally,this paper analyzes the existing problems in robot calibration,which may be worth researching in the future.

I. INTRODUCTION

INDUSTIRAL robots are an important automation equipment of modern manufacturing industry [1]-[6], which integrate the advanced technology of multi-disciplinary, such as machinery, electronics, control, computer, sensor, artificial intelligence, etc. Electric welding robots, distribution robots,assembly robots and handling robots have been widely used in industrial production activities [7]-[12]. At present, one of the development directions of industrial robots is focused on how to improve positioning accuracy, which has also become one of the key technologies for the practical application of off-line programming methods in advanced robotic manufacturing systems. The pose error of the robot can be greatly reduced by calibration, the absolute accuracy of the robot can be improved for the level of repeat accuracy [13]-[20]. The required target positions of the end-effector of robot are specified in working space, these positions are reached by controlling the joint angle of robot. However, off-line programming method ignores the pose error and the target positions error in the actual production environment, it believes that the robot can completely track the target trajectory, which is set by the software [21]-[25]. Due to the errors in the structural parameters of robot and the influence of robot dynamics, the actual running trajectory of robot is greatly deviated from the programming and simulation trajectories. Errors caused by structural parameters can be compensated by calibrating the kinematic model of the robot[26], [27]. In general, high-speed robots, large-load robots,trajectory tracking errors are mainly caused by dynamic factors, such as centrifugal force, Coriolis force and dynamic coupling for the joints of robot, etc. [28]-[30]. The dynamic model of robot can be used to compensate for these dynamic factors.

Due to the calibration model of the robot contains many parameters, which are uncertain, their values have a great influence on the calibration methods. In the high-speed operation, the uncertainty of sensitive parameters is particularly serious [31]-[36]. The parameter identification methods have a great significance for the development of model-based controllers. In general, the parameter identification procedures include modeling, experiment design, data collection, signal processing, parameter identification and model verification [37]-[42]. The final step of the calibration procedure is model verification, where the accuracy specifications should be satisfied calibration model,which is verified by the researchers. If the model fails the verification test, one or more steps of the identification procedure are repeated until the test is passed.

Error parameter identification is a process of using some algorithms and indicators to solve the parameters of error model. The choice of model and model parameters directly affects the identification and compensation results, which has an influence on the calibration accuracy [43]-[50]. Numerous researchers have conducted in-depth research on parameter identification and obtained many research results [51]-[56].Gan et al. [1] proposed a method for robot calibration of kinematic parameters, which was based on the draw-string displacement sensor, the kinematic parameters were successfully identified. Park et al. [3] proposed a method for estimating kinematic parameters by using a structured laser module (SLM) and a stationary camera, the validity of parameter calibration of 7-degree of freedom (DOF)humanoid robot arm and 4-DOF manipulator was verified by experiment. Wang et al. [4] used the screw axis identification(SAI) method based on product of exponentials (POE) model,two simulation experiments verified that the method had high accuracy and good stability. Li et al. [5] presented a searching method for the optimal measurement pose number to improve the identification accuracy. After calibration, the pose errors were 1.54, 1.61 and 0.86 mm, which were better than the 7.79,7.62 and 8.29 mm before calibration.

In this paper, the research contributions of this work contain:

1) The error parameter identification of serial and parallel robots is summarized. The parameter identification algorithms of complex serial and parallel robot are not involved, then the parameter identification algorithms of simple serial and parallel robot are introduced.

2) Identification algorithms, calibration models, verifications and applications are explained, the related research work at home and abroad is reviewed.

3) Various problems in robot calibration are discussed,which provide new ideas for future research.

For the rest structure of this paper, Section II states identification model and procedure of robot accuracy calibration. Section III presents a brief review of robot calibration algorithm. Section IV gives some classical applications of calibration method. Section V summarizes the discussions. Finally, conclusions are drawn in Section VI.

II. MODEL AND IDENTIFICATION PROCEDURE

In this section, the kinematics model and dynamics model of the robot are presented for robot modeling. Then, the procedure of robot calibration based on these models is introduced.

A. Kinematic Model

The robot structure is composed of a series of link mechanisms connected by joints. In order to describe the relationship between the joints, it is necessary to establish a kinematic model of the robot [57]-[63]. Then the relative position relationship between these joint coordinate systems is described by the homogeneous transformation matrix based on this model [64]-[70]. Finally, the functional relationship between the end-effector of the robot and each joint parameter is also accurately obtained.

1) Denavit-Hartenberg (D-H) Model

Recently, the most commonly used modeling method is the D-H model, which was proposed by Denavit and Hartenberg,and now the kinematic model in most industrial robot controllers is the D-H model [1], [17]. The direct kinematic model of robot can be described as 2) Modified Denavit-Hartenberg (MDH) Model

Fig. 1. Robot RS10N [9]. Leica laser tracking system is used to measure the position of robot’s end-effector.

In order to solve the inconsistency between the description method of the rigid body in the 3-D drawing software and the coordinate system description method in the traditional D-H model, which causes the inconvenience of the designer to modify the structure of the robot, MDH model is proposed to establish kinematics model of the robot, which has better kinematic forward and reverse solutions [9], [71]. The direct MDH kinematic model of robot can be described asi

3) POE Model

To solve the problem of singularity, the POE model is used to describe the kinematics model of robot [11], [12]. POE model can accurately describe the real-time robot’s endeffector under the action of rotation angle. The expression of robot’s end-effector is constructed by the motion of rigid body between adjacent joints. After numerous end-effectors are collected, the robot parameters are identified and compensated to achieve the calibration of robot. The kinematic model based on POE formula can be described as

4) Stone (S)-Model

Stone added two parameters into the D-H model for establishing the S model, the transformation between link coordinate systems is described by 6 parameters. Compared with the D-H model, the modeling process of S model is more flexible, and the origin position of the link coordinate system is arranged arbitrarily. The S kinematic model is presented by

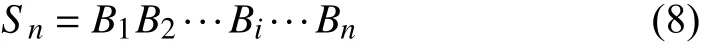
where Biis transformation matrix.

However, the S model adds additional parameters, which makes the calibration model more complicated, the kinematics parameters of the robot cannot be accurately identified.

5) Complete and Parametrically Continuous (CPC) Model

CPC model is similar to S model, which also adds two parameters into D-H model. It makes up for the discontinuity and incompleteness of D-H model. In CPC model, the direction of joint axis is described by three parameters, the position relationship of the adjacent coordinate system is presented by other three parameters describe. CPC model uses 6n link parameters to build the kinematics model, but some of the parameters are redundant, the identification of kinematics parameters is inaccurate.

For CPC model, the transformation matrix can be written as B=Q×V, where V is related to link parameters and Q is related to joint angles.

6) Sheth-Uicker Model

The D-H model commonly used in kinematic modeling is suitable for low-level links, while the Sheth-Uicker model is suitable for describing high-level links. The Sheth-Uicker model was proposed by P. N. Sheth and J. J. Uicker Jr in 1971. They used instantaneous coincident coordinate system to describe the motion of the robot. The instantaneous coincident coordinate system is fixed in the absolute coordinate system and has the same orientation as the dynamic coordinate system.

For Sheth-Uicker model, the transformation matrix can be expressed by T =J(θ)×S , where J(θ) is the Jacobian matrix of robot, S is the displacement of robot.

B. Dynamic Model

The research on the dynamics of industrial robots is the relationship between joint force, torque and joint motion. The main purpose is to use dynamic model to calculate the torque,which should be provided by the actuator of each joint when the joints of the industrial robot perform target movements[8], [37]. The torque value is used for the control of the robot.

Industrial robots are a complex dynamic system with severe non-linearity. The joint force, torque and joint motion parameters are mostly trigonometric functions. There is serious coupling relationship, the motion of each joint is coupled with each other, the force and moment are also coupled with each other. Hence, in order to analyze the dynamic characteristics of industrial robots, it is necessary to use a very systematic analysis method. There are many methods for the dynamic modeling of industrial robots, such as Lagrange method, Newton-Euler method, Gauss method,Kane method, operator algebra method, etc. [43], [44]. No matter which modeling method is adopted, the final dynamic model of the determined industrial robot system is the same.The dynamic model is derived from Lagrangian equation and expressed as follows:

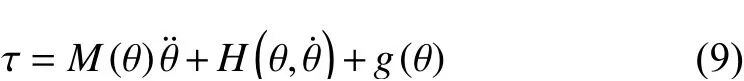
The model-based control schemes mainly contain the calculated torque control, dynamic feed-forward control, etc.In order to achieve the accurate tracking of the trajectory through these control schemes, it is necessary that the dynamic model in the control scheme is consistent with the actual dynamic characteristics of the robot [55]. The dynamic models obtained by various typical modeling methods are just the ideal results. In practical situations, there are many factors that affect robot dynamics, such as deviations caused by processing, assembly, and uneven material distribution. Some of these factors are inaccurate modeled. In order to reduce the complexity of the dynamic model, the ideal dynamic modeling method does not fully consider the effect of these factors. Hence, the obtained dynamic model is different from the actual robot dynamic characteristics [47], [55]. The deviation of the dynamic model is mapped into the control scheme, which causes the tracking error of the trajectory.

In order to improve the tracking accuracy of the robot, it is necessary to compensate these factors in the dynamic model.However, many of these factors can not be modeled or accurately modeled. In addition, adding additional models makes the dynamic model more complex, the real-time performance of dynamic calculation is reduced, the control hardware is more demanding, and the control cost is increased. Hence, from the two aspects of improving accuracy and reducing cost, the dynamic parameter identification method is adopted. The effects of other factors are included in the inertial parameters of the robot through the identification process without changing the dynamic model. A group of comprehensive parameters satisfying the accuracy of dynamic calculation are obtained, which not only improves the accuracy, but also saves the cost. Since the analysis of robot dynamics model has advantages in improving calibration accuracy, the identification of dynamic parameters has become a hot issue in the field of robot dynamics and control.

As a hot issue in the field of robot, the identification of dynamic parameters has attracted the attention of researchers at home and abroad, and a series of methods with application value have been proposed successively. In general, it can be divided into disintegration measurement method, CAD method and overall identification method.

1) The disintegration measurement method is to disassemble the robot into several parts, such as the big arm, the small arm,etc. The mechanical arms of these parts are measured to obtain the centroid and other parameters, then the inertia parameter calculation formula is used to find the inertia parameters of each part of the robot arm.

2) The CAD method is developed with computer graphics,which does not need to disintegrate the robot. It only needs to give the designed 3-D model of the robot, and the software can automatically calculate the parameters.

3) The overall identification method gives the robot a designed trajectory of the joint to be identified. In the process of the robot moving along the preset trajectory, the driving torque and joint rotation angle of joint are collected. Besides,the sampling value is also brought into identification model.Finally, the value of the inertia parameter is accurately calculated by identification algorithm.

The identification of kinematic parameters is of great significance for improving the accuracy of the kinematic model, which has received great attention from scholars at home and abroad. The overall identification method has been widely used, which can take into account the effects of dynamic factors in the actual environment.

C. Identification Procedure

First, a kinematic model of the robot is established. The purpose of robot kinematic modeling is to find the corresponding relationship between the end-effector and the joint values of the robot. This model contains a set of parameters of a specific robot geometry. Robot kinematic calibration can identify the optimal value of the robot geometry parameters [72]-[78].

The robot accuracy calibration procedure is an integrated process of modeling, measurement, parameter identification and error compensation [79]-[85].

1) Recently, the most commonly used kinematics model is the D-H model. The idea of this model is to fix the link coordinate system at the link joint, which is also correlated with the homogeneous coordinate transformation between the adjacent coordinate systems.

2) In the process of robot calibration, measurement is an important factor affecting the calibration accuracy. The most commonly used data for identification is position data. The position measurement tools commonly used for robot calibration include ballbars, coordinate measuring machines,and laser trackers, etc.

3) Kinematic parameter identification is the process of optimizing error parameters in this model by using numerical optimization algorithm. Its main purpose is to provide the error information of kinematic parameters from the measurement data under external interference. The most commonly used optimization algorithm is the least squares algorithm.

4) Error compensation is the last step in the robot calibration process, and it is also the key step to check the effectiveness of the previous steps. Error compensation is to compensate the error identified by the error model to the robot controller for improving the accuracy of the robot end-effector.

The calibration procedure generally contains the following steps. Firstly, a robot kinematic model that accurately represents actual parameters is established. According to the mathematical model, the measurement scheme is designed,then the end-effector of the robot is measured by a highprecision measurement device. Next, parameter identification algorithm is proposed, which is carried out by algorithm program. Finally, the original robot kinematic model is accurately compensated.

The above calibration process is described with a flowchart depicted in Fig. 2.

III. BRIEF REVIEW OF ROBOT CALIBRATION ALGORITHM

Fig. 2. The flow chart calibration procedure.

In this section, numerous robot calibration algorithms and related references are introduced, and the advantages and disadvantages of these algorithms are analyzed. Error parameter identification is the procedure of solving the error model parameters using some algorithms and indicators. The choice of model and model parameters directly affects the identification and compensation results, thus affecting the calibration accuracy. According to the research of Song [16]and Mao [18], the error identification model has complete error parameters, which are independent of each other. The error model is continuous and differentiable in the workspace.After constructing the error model and obtaining the measurement data, a set of error equations can be established.Error identification is the process of solving the error model equations. Commonly used identification methods are least squares algorithm, maximum likelihood estimation algorithm,genetic algorithm, extended Kalman and particle filter algorithm, simulated annealing algorithm [61], [62], etc. Next,the research results of these calibration algorithms and the types of calibration error are introduced in this paper.

There are various sources of error that affect the positioning accuracy of the robot. According to the error characteristics, it can be divided into deterministic error, time-varying error, and random error. Deterministic error does not change with time,which can be measured and identified in advance, such as the geometric error. Time-varying error is changing with time, but there are certain rules to follow, such as error caused by temperature. Random error has no obvious rules and cannot be accurately measured in advance, but it can be evaluated by statistical methods, such as the noise of external vibration and the operating error.

According to different sources of error, it can be divided into geometric parameter error and non-geometric parameter error. The geometric parameter error is mainly composed of the link parameters error and the joint rotation angle parameters error. Non-geometric error contains joint flexibility, friction, joint clearance, etc. In this section, the non-geometric error is described in detail.

1) Extensive high-performance robots generally use harmonic drivers with relative flexibility to drive joint motion,joint flexibility cannot be ignored. When the joint is flexible, a torque is generated by the elastic motion, then the obtained joint rotation angle has a certain deviation from the actual value, which causes identification error.

2) Friction is a very complex nonlinear phenomenon, and it cannot be accurately modeled in most situations. The current commonly used method is to assume a linear or simple nonlinear friction model. There is a deviation between the model and the actual friction phenomenon, thus the friction torque calculated by the robot model also has an error. There is a deviation in the torque of the robot, which causes the trajectory tracking error.

3) Generally speaking, the robot is composed of several links connected by joints. Due to manufacturing error,installation error or other reasons, there must be a gap between the shaft and the shaft hole of each joint. Therefore,under the action of joint force, the shaft inevitably produces deflection and displacement in shaft hole, which causes identification error.

A brief summary and description of these calibration methods are shown in Table I (see top of next page), including method name, brief description, references and applications,etc. In next content of this section, several typical calibration algorithms are summarized and introduced briefly.

A comparison of these calibration methods is introduced in Table I. The least squares algorithm is a simple optimization algorithm, which is suitable for solving various regression problems. Its advantages are short running time and strong search ability. However, it is easy to fall into overfitting problem. Least squares algorithm with regularization is suitable for solving various regression problems. It can effectively avoid the problem of overfitting and has a strong search ability. Its disadvantage is easy to fall into local extremes. Levenberg-Marquardt algorithm is suitable for solving nonlinear least squares problems. Its advantages are simple algorithm and fast solution speed. However, it is easy to fall into local extreme values. The extended Kalman and particle filter algorithm is an efficient recursive filter, which can be used to solve the problem of noise and interference in the observation data. Its advantages are strong search ability and short running time. The disadvantage is easy to fall into local extremes. The maximum likelihood estimation algorithm is used to estimate the parameters of a probabilistic model, which has the advantages of convenient calculation and high efficiency. Nevertheless, it cannot solve small sample problem.

Genetic algorithm can deal with the constraints well, jump out of the local optimum and obtain the global optimal solution. Its shortcomings are slow convergence and easy to be affected by the parameters. Improved whale swarm algorithm (IWSA) algorithm has strong search ability and can effectively avoid local extreme problem, but its algorithm is complex and its calculation cost is large. Simultaneous calibration of 2-D laser and robot (SCALAR) algorithm is suitable for solving optimization problem with constraints,which can avoid local extreme problem, but its disadvantages are high computation cost and long running time.

The self-calibration algorithm has a strong adaptive ability,but its algorithm is complex and the solution speed is slow.

A. Least Squares Algorithm

The most widely used parameter identification method is the least squares algorithm, which is to find the method of minimizing the error between the theoretical data and the actual measurement data to achieve the solution of the error parameters. A method of robot kinematic parameters calibration based on a draw-string displacement sensor was proposed by Gan et al. [1]. The 3-D schematic model of position measuring system by drawstring displacement sensors was shown in Fig. 3, which contained three parts: thebase, the universal joint, and the drawstring displacement sensor. The position data of a point was converted into the length data of the drawstring displacement sensor by this system. Then, this paper established a kinematic error model of robot. The position measurement system was composed of four displacement sensors in this model, the actual position of the robot end-effector was measured by the system. According to the deviation of the robot end-effector, the parameter deviation of the robot was identified by the least-squares method. The accuracy of the absolute positioning for robot end-effector was improved by using the Cartesian space compensation method. After the calibration, the absolute positioning accuracy was greatly improved by experiments on the EFORT ER3A robot. Nubiola and Bonev [8] made extensive experiments, which used 29-parameter calibration model to improve the absolute accuracy of the ABB IRB1600 industrial robot. All possible geometric errors were considered by the error model, then it used the least squares algorithm to find the 29 error parameters, which were most suitable for laser tracker measurement. Similar to most other studies, the positioning accuracy of the robot with 1000 measurements was verified by the robot joint space. The average/maximum position error of the robot was reduced from 0.968 mm/2.158 mm to 0.364 mm/0.696 mm, respectively after calibration. Moreover, to solve the ill-conditioning problem caused by multicollinearity that identified Jacobian with limited pose measurements. Huang et al. [49] introduced a 6-DOF hybrid robotic model based on polished aspheric lenses. This method used ordinary least squares iteration to estimate the encoder offsets until the requirement was satisfied by the linearized regression model, its validity was verified by experiments.

TABLE I BRIEF SUMMARY OF CALIBRATION ALGORITHMS

Fig. 3. The 3-D schematic model of position measuring system by drawstring displacement sensors [1]. It contained three parts: the base, the universal joint, and the drawstring displacement sensor.

B. Least Squares Algorithm with Regularization

Kinematic calibration method can improve the accuracy of the parallel kinematic machine (PKM). With the development of computer technology, PKM’s kinematic calibration technology has made great progress. However, its application is still limited in non-redundant PKM, these existing calibration methods still cannot solve the calibration of overconstraint of PKM. Jiang et al. [46] presented the modeling and identification of kinematic errors in over-constrained PKM. Kinematic errors of over-constrained PKM were identified by the least squares algorithm with regularization.Finally, simulation and experimental results confirmed the feasibility of the proposed method.

C. Levenberg-Marquardt Algorithm

Levenberg-Marquardt algorithm is an optimization algorithm for the least squares algorithm. A regularization factor is added to prevent the over-fitting problem in the data training procedure and enhance the stability of the least squares algorithm. Wu and Shi [48] presented an optimization method combining Levenberg-Marquadt method and interior point method. This paper established an error model of multiconstraint parallel continuum robot (MPCR). Structure of the MPCR prototype was shown in Fig. 4. Connecting rods with intermediate constraints was through rod end bearing, which allowed this connection point to be fixed on the rod without external moment constraints. The rods were clamped at the disk of constraint 5. The center of constraint disk 1 was global framework prototype. Then, the numerical solv-ability and performance of the error model under noise disturbance was expressed by simulation results. The calibration method was experimentally verified on this model. Experimental tip positions were matched by the model, thus mean and maximum errors were 0.8% and 1.8% for the total length,which verified the effectiveness of this method.

Fig. 4. Structure of the MPCR prototype [48]. Connecting rods with constraints was through rod end bearing. Rods were clamped at the disk of constraint 5. The center of constraint disk 1 was global framework prototype.

D. Extended Kalman and Particle Filter Algorithm

Since the Kalman filtering theory was put forward in the last century, Kalman filtering has made outstanding contributions to the development of cybernetics and information theory.Kalman filtering, extended Kalman filtering, unscented Kalman filtering, particle filtering and other methods can be used to make predictions for obtaining an accurate state truth value in the next moment. These methods have been used in many aspects, such as pose solution and trajectory planning,etc. The essence of the Kalman filter is a parameterized Bayesian model. More accurate state estimation at the moment is finally obtained by combining the initial state estimation of the system at the next moment and the measured feedback. To solve the problem of non-Gaussian noise and high nonlinearity, Jiang et al. [9] introduced a new calibration method based on extended Kalman filter (EKF) and particle filter algorithm (PF). Firstly, this paper established its error model and the kinematic model, the kinematic parameters of the robot were identified by EKF algorithm. However, the identification accuracy of robot kinematic system with non-Gaussian noise systems was affected by the EKF algorithm,which had a kind of linear truncation error. The PF algorithm could solve this problem well, but the prior distribution of the initial values affected the calibration accuracy. Hence, the prior value of the PF algorithm used the calibration value of the EKF algorithm, and then, the robot kinematic parameters were calibrated by PF algorithm.

Finally, a large number of experimental results validated the feasibility of the method, which could significantly improve the positioning accuracy of the robot. Kalman filter (KF) and particle filter was proposed by Du and Zhang [17], which estimated the position of the robot. The reliability and accuracy of pose measurements were improved by this method. Then, the kinematic parameter errors were estimated by the extended KF. Compared with the existing calibration methods, this method had the advantage that it did not contain the complicated steps, such as laser alignment, camera calibration, etc. It had more autonomous in the calibration procedure. In addition, it could improve the accuracy of calibration by reducing complex steps. This method had better accuracy, which validated by numerous experiments on the GOGOL GRB3016 robot.

E. Maximum Likelihood Estimation Algorithm

Parameter estimation is the process of calculating system model parameters, which uses input and output data of system, when the structure of the system model is known. The maximum likelihood estimation algorithm proposed by Gauss and Fisher is one of the most widely used parameter estimation methods. The method is based on the intuitive principle of maximum likelihood. Its principle is to randomly select n sets of sample observations from the model population. Then, the most reasonable parameter estimator should maximize the probability of selecting the n sets of sample observations from the model, but the purpose of least squares algorithm is to get the parameter estimator that makes the model best fit the sample data. The advantages of maximum likelihood estimation mainly contain good convergence, simple iterative methods, and more practicality.To solve the problem of complex kinematic error, a new robot calibration compensation method was proposed by Ma et al.[29]. In this paper, it used a FANUC LR Mate200i robot with a RJ3 controller for experimental research, photograph of FANUC LR Mate 200i robot was shown in Fig. 5 (see top of next page). This method used a laser tracker to measure position data from three different orientation for the measurement tool installed on the robot. Nominal kinematics of the robot was enhanced by the generalized error matrix.Then, model parameters were estimated by maximum likelihood estimation method. The updated joint commands were calculated by Jacobian-based search method, which compensated for kinematic errors. The proposed method was compared with the traditional calibration method by experiments. Numerous experiments were performed on the FANUC LR Mate200i robot. 79.4% of the measurement error was presented by traditional kinematic error model. However,97.0% of the measurement error could be described by new model, which contained the measurements of 250 poses.Experimental results showed the feasibility of the new method.

Fig. 5. Photograph of FANUC LR Mate 200i robot [29]. It had a RJ3 controller for experimental research. This method used a laser tracker to measure the position data from three different orientation for the measurement tool installed on the robot.

Fig. 6. Structure of the serial parallel polishing machine tool [50]. It contained a 3-RPS parallel robot and two single-axis NC tables. The genetic algorithm was used to identify kinematics parameters.

F. Genetic Algorithm

Genetic algorithm is a computational model that simulates the natural selection and genetic mechanism of Darwin’s theory of biological evolution. It is a method of searching the optimal solution by simulating natural evolution. In the 21st century, genetic algorithms have developed rapidly, which has become a hot topic in the theoretical research and applied research. Fan et al. [50] addressed a new calibration method of a parallel mechanism, which was based on genetic algorithm and kinematics model. Structure of the serial parallel polishing machine tool was shown in Fig. 6, which contained a 3-RPS parallel robot and two single-axis NC tables. The parallel robot was composed of three identical length changeable limbs, a lower platform, and a moving platform. Electric cylinder driven limbs. The lower platform of the parallel robot was fixed on a single-axis NC table. The belt polishing tool was fixed on another single-axis numerical control (NC) table. Then, the measurement of the absolute position of the robot could be avoided by this method.Calibration experiments were performed on the robot. After calibration, the accuracy of positioning error increased from 0.083 mm to 0.018 mm, which was improved by about 78.3%.To improve calibration accuracy of the 2-DOF overconstrained parallel mechanism (PM), the kinematic calibration problem of over-constrained PM was presented by Sun et al. [80]. First, a non-linear error model was established.Then, it used the genetic algorithm to identify the error parameters, error compensation was achieved by the controller. Finally, the extensive experimental results showed that the orientation accuracy was improved by 93.96% and 90.38% for the 2-DOF hyper-constrained PM.

G. Improved IWSA Algorithm

Fig. 7. Two-segment hydraulic leg [65]. It contained a hydraulic actuator and two segments (calf and thigh). The IWSA was used to identify the kinematic parameters of the robot leg.

Zhong et al. [65] designed a kinematic model of a twosegment hydraulic robot leg, which was shown in Fig. 7. The leg structure contained a hydraulic actuator and two segments(calf and thigh). However, this model was highly nonlinear,using traditional techniques was difficult to acquire accurate parameters. A constrained multimodal function optimization problem could replace this problem. Then, an improved whale swarm algorithm (IWSA) was proposed to identify kinematic parameters. The search ability of IWSA was improved by using some improvement strategies. Actual calibration experiments verified the superiority of this method. This method provides an accurate calibration algorithm for kinematic parameters of robot legs, which avoids the problem of calculating kinematics calibration with complex mathematical methods. The proposed method is cheap and convenient, which does not need expensive external measurement systems or complex calibration steps, which has the good practicability.

H. SCALAR Algorithm

Lembono et al. [60] developed SCALAR algorithm, a calibration method that could solve the problem of a 6-DOF robot kinematic parameters calibration and the 2-D laser rangefinder parameters calibration. The calibration device only required a flat plate and a sharp tool-tip. Calibration setup was shown in Fig. 8. The flat plate was placed in an accessible robot workspace, a sharp tool-tip and the LRF were mounted on the robot flange. There were two small holes on the plate, which were separated by a known distance D. Due to the calibration was a non-linear optimization problem,planar and distance constraints were provided by laser and tool-tip, Levenberg-Marquardt algorithm was utilized to solve the optimization problem. This algorithm could reduce the average/maximum tool position error from 0.44 mm, 1.41 mm to 0.19 mm, 0.50 mm by extensive experiments.identify the kinematic parameter errors. Hence, higher position accuracy of robot could be achieved by experimental results.

Fig. 9. Six-degrees-of-freedom Sterling series FARO arm [31]. It contained the a-b-c-d-e-f degree rotation and the typical 2-2-2 configuration. A selfcentering active probe was used to analyze the collecting data method.

Fig. 8. Calibration setup: a 6-DOF industrial robot equipped with a 2-D laser range finder and a sharp tool [60]. Planar and distance constraints were provided by laser and tool-tip, Levenberg-Marquardt algorithm was utilized to solved the optimization problem.

I. Self-Calibration Algorithm

To explain the identifying parameters model of an articulated arm coordinate measuring machine (AACMM), a self-centering active probe was introduced by Santolaria et al.[31]. The AACMM was a six-degree-of-freedom sterling series FARO arm, which contained the a-b-c-d-e-f degree rotation and the typical 2-2-2 configuration. The structure of AACMM was shown in Fig. 9 . Compared with the usual standard methods, the capture time and the number of positions of the gauge were greatly reduced by this method. It determined a homogeneous transformation matrix that associated the reference system of the probe with the AACMM last reference system for a single sphere. In addition, the effectiveness of this method was proved by extensive experiments. Zhu et al. [78] addressed a method for self-calibration of dual-manipulator, the actual kinematic parameters of the robot was estimated by virtual constraints based on this method. Firstly, robot kinematic model based on linear constraints was established, the positioning error was represented by the kinematic parameter error. Then, the optimal calibration poses of the robot under these constraints were generated by the particle swarm optimization algorithm.Finally, the Levenberg-Marquardt algorithm was used to

IV. APPLICATIONS OF ROBOT CALIBRATION METHOD

Robot parameter calibration is an important work before utilizing the robot [86]-[91]. Ensuring the precise matching of the robot controller and the robot body is an important prerequisite for the performance of the robot controller, which guarantees the application ability of the robot in the industrial field. Such as offline programming technology, the practice in the simulation environment can be directly applied to the actual project without error, which speeds up the progress of the industrial robot projects [92]-[98]. Robot parameter identification algorithm is of great significance for improving the calibration accuracy, and has attracted great attention from scholars at home and abroad [99]-[105].

Recently, robot calibration algorithm is applied to many areas [106]-[112]. In this section, some classical applications of robot calibration are discussed.

A. Calibration for Overconstrained Spatial Translational Parallel Manipulators

Li et al. [74] presented a calibration method for an overconstrained spatial translational parallel robot. This method based on the calibration of a Tri-pyramid overconstrained parallel robot was verified its feasibility. The proposed method converted the overconstrained mechanism of the robot into a non-overconstrained mechanism. First, the kinematics model of the original overconstrained parallel robot was established. Then, based on the robot’s comprehensive kinematics model and measured data, the robot parameters were identified by least squares method.Finally, accuracy improvements on the order of 90% were obtained after calibration of the robot.

B. Calibration of 6-DOF Industrial Robots

Xie et al. [76] developed a new calibration method based on line structured light measurement system. This system mounted on the robot end-effector was used as a tool to obtain measurement information. An error model was established by this method, the center of the sphere was measured by the system. Since the subtraction eliminated the actual coordinates of the sphere center, additional high-precision instruments were unnecessary. This method reduced the complicated steps of the calibration procedure and improved the calibration accuracy. Simulation and the experimental results verified the feasibility of the method.

C. Calibration of Eight Degree-of-Freedom Manipulators

To improve the calibration performance of the eight degreeof-freedom manipulator, a configuration optimization method was presented by Chen et al. [77]. The numerical method was used to analyze the relationship between the comprehensive quality index and the calibration accuracy. Then, a comprehensive quality index for the calibration model was established by statistical theory, which was solved by particle swarm optimization (PSO) algorithm. After calibration, the calibration accuracy was improved by the proposed optimal configuration method.

D. Multi-robots System Calibration

Qiao et al. [79] applied a new calibration method for multirobot systems, which was based on the POE model without nominal kinematic parameters. This method reduced requirements for kinematic parameters and simplified the modeling procedure of kinematic parameters. Simulation and experimental results showed that the model had good convergence, the position error after calibration was only 0.145% of the original error.

E. Other Applications

Jiang et al. [81] introduced a complex structure of the parallel kinematic machine (PKM), which used the theoretical and technique methods for improving the kinematic accuracy of PKM. Then, the PKM kinematic error model was established. Several key preparations were important to improve calibration accuracy, including installing a grid encoder, automatically measuring kinematic information, etc.Campisano et al. [82] proposed a method to improve the accuracy of the continuum manipulators calibration by introducing feedback from the orientation sensor. Mao et al.[83] developed a collaborative accuracy scheme for kinematic calibration problem, a minimax search algorithm is applied to improve collaborative accuracy of the orientation and positioning.

V. DISCUSSIONS

In this section, a new method of robot calibration is introduced, which takes into account measurement noise and some external constraints, thus the calibration accuracy is improved after calibration. Then, the existing challenges and open problems in robot calibration are discussed [113]-[118].

To solve the non-negligible flexibility problem of industrial robots, a rigid-flexible coupling error model for robot nonkinematic calibration was proposed by Chen et al. [72].Simulation experiments showed that compliance errors were the main factor for inaccurate robot calibration. Different from the above methods, an improved method was presented for full pose measurement and parameter identification, which could reduce the impact of measurement noise. This method was based on a self-adaption particle swarm optimization algorithm and an improved Levenberg-Marquardt algorithm,which took into account the external constraints. The simulation results showed that the proposed error model had better identification accuracy and stability.

With the continuous development of science and technology, industrial robots have gradually become the core equipment of modern industry [119]-[124]. With the widespread application of off-line programming robots, robot calibration accuracy has become a research hot issue. This paper discusses the application of some calibration algorithms,which has a certain reference value for researchers.

Through the above summary, it can be found that many researchers have made numerous achievements in robot calibration. However, there are still extensive problems in robot calibration, which need further study and discussion.

1) Recently, a laser tracker or a coordinate measuring instrument is often used to measure the actual position of the robot end-effector. Due to the limitation of the working range of the receiver and transmitter of the measuring instrument, it is difficult to determine the spatial coordinate when the robot moves to a certain position. Therefore, it is necessary to use a combination of multiple measuring instrument to reduce the measurement blind zone, so the cost of calibration is increased. In order to facilitate the processing of measurement data, it is necessary to convert the coordinate systems of multiple measurement instrument to the same coordinate system. However, it has inaccurate measurement results with the transfer station errors. Hence, how to reduce the transfer station errors is a problem to be researched in the future.

2) In the calibration of the robot parameters, the links of robot have deformation based on the effect of gravity. At the same time, torsional deformation also occurs in the joint transmission system on the gravity torque effect of the postposition links, especially for large span robot. Since each angle is different, the deformation caused by gravity and gravity torque is also different in the measurement process,which has randomness in the calibration of the robot parameters. Hence, how to take effective measures to reduce the effect of gravity and gravity torque is significant to improve the calibration accuracy of robot parameters.

3) At present, most of the calibration techniques are still in experimental environment. There are few researches on the fast calibration. In terms of open-loop calibration, external measuring instrument is used to obtain experimental data.Then, it takes a long time to achieve this procedure, which is only suitable for the laboratory environment. At the same time, due to the uncertainty of measurement, it can only ensure that the error in the calibration area of the manipulator is small. However, it is difficult to satisfy the requirements of positioning accuracy for any position in the working space,which hinders the development of autonomous research of the robot. In the past several years, some researchers have studied the uncertainty distribution regular of each parameter, it is also one of the hot issues to improve the absolute positioning accuracy of the robot in the future.

4) During the measurement process, the measurement noise has a certain impact on the calibration result. In order to reduce the measurement noise, it is necessary to choose a suitable structure to maximize the reflection of the robot parameter error to obtain a better effect of parameter identification. Currently, most researchers make use of the observability index for the objective function to select the best optimal measurement structure. Nevertheless, the proposed methods have not considered the influence of the model parameter error on the positioning accuracy of the endeffector. Therefore, the research on the relationship between model parameter error and the positioning accuracy of the end-effector will become one of the hot spots of calibration technology research.

5) With the increasing requirements for robot autonomy,researchers have proposed the real-time of robot calibration technology. Neural network is an intelligent method, which can not only replace any continuous non-linear function for calculation, but also has strong independent learning ability and robustness. It provides convenience to adaptive network reconstruction. Vision measurement method can quickly achieve the measurement of the end-effector. At the same time, it achieves a high autonomy for robot. Therefore, the convergence efficiency of the neural network and the accuracy of the visual measurement system have been greatly improved, which show great advantages in autonomy and real-time. This technology will attract widespread attention of the researchers.

VI. CONCLUSIONS

The robot calibration method can improve its absolute pose accuracy, which has a high practical value in the field of robot.

This paper summarizes the research status and application fields of robot calibration technology. In the robot parameter calibration, error parameter model based on the transfer relationship of each link of the robot is established. To obtain the optimal solution, the error model is linearized or an optimization algorithm is discussed. However, non-parametric calibration uses intelligent algorithms to solve the problem of nonlinear calibration. Non-parametric calibration gives a new research idea for researchers, which has a close relationship with artificial intelligence. Then, various calibration methods and some classical applications of robot calibration are discussed in this paper. Besides, advantages and disadvantages of each calibration algorithm are presented. On this basis, the existing problems of robot calibration are also discussed. With the development of robot calibration research work, its trend has the following directions.

1) The robot calibration process is developing in the direction of artificial intelligence. Neural network, deep learning and big data will be gradually applied in kinematic modeling, parameter identification and error compensation.Thus, robot calibration has higher accuracy, better calibration results and stronger robustness.

2) With the improvement of the accuracy of measurement system and the diversity of calibration methods, nongeometric parameter calibration will be better studied and the calibration accuracy will be further improved.

3) Machine vision is a rapidly developing branch in the field of robots. If machine vision is combined with artificial intelligence, robot calibration will make great progress.