Adaptive Control of a Two-Link Robot Using Batch Least-Square Identifier

Mostafa Bagheri, Iasson Karafyllis, Peiman Naseradinmousavi, and Miroslav Krstić, Fellow, IEEE

Abstract—We design a regulation-triggered adaptive controller for robot manipulators to efficiently estimate unknown parameters and to achieve asymptotic stability in the presence of coupled uncertainties. Robot manipulators are widely used in telemanipulation systems where they are subject to model and environmental uncertainties. Using conventional control algorithms on such systems can cause not only poor control performance, but also expensive computational costs and catastrophic instabilities. Therefore, system uncertainties need to be estimated through designing a computationally efficient adaptive control law. We focus on robot manipulators as an example of a highly nonlinear system. As a case study, a 2-DOF manipulator subject to four parametric uncertainties is investigated. First, the dynamic equations of the manipulator are derived, and the corresponding regressor matrix is constructed for the unknown parameters. For a general nonlinear system, a theorem is presented to guarantee the asymptotic stability of the system and the convergence of parameters’ estimations. Finally,simulation results are discussed for a two-link manipulator, and the performance of the proposed scheme is thoroughly evaluated.

I. INTRODUCTION

ROBOT manipulators are widely used in various applications to track desired trajectories on account of their reliable, fast, and precise motions in executing tasks such as moving debris and turning valves [1], [2], while, as expected, consuming a significant amount of lumped energy[3]. Remote manipulators provide the capability of executing tasks safely and autonomously at dangerous or unreachable locations. However, they inevitably operate within different environments subject to numerous uncertainties or large time delays [4]. These uncertainties including, but not limited to,the length, mass, and inertia of the links as well as the manipulator payloads are some of the mentioned uncertainties.The detrimental impact of uncertainties is well-established,which plays the most significant role in degrading remote perception, manipulation, and destabilizing systems. Adaptive control is an effective approach to control these highly nonlinear systems under parametric uncertainties.

Considerable research efforts have been devoted to the adaptive control of linear and nonlinear finite-dimensional systems, see [5]-[7]. Adaptive controllers are designed to compensate for the detrimental effects of system uncertainties in addition to enabling the system to follow the desired trajectory [8]. Developing adaptive control schemes for robots has received much attention in the last three decades [9]-[12].Using the algorithm formulated by Slotine and Li [13], Spong[14] presented the adaptive control results for flexible joint robot manipulators under the assumption of weak joint elasticity, while adaptive motion control for rigid robots was studied by Ortega and Spong in [15].

The adaptive control scheme derived in [16] requires the joints’ accelerations for its implementation, through estimating the acceleration from the measured velocity, which inevitably needs sufficient encoder resolution and fast sampling. Slotine and Li [17] presented a combinatorial adaptive controller for robot manipulators, and the parameter adaptation is driven by both tracking and prediction errors. These very sophisticated schemes need the calculation of many complicated analytical expressions at each iteration leading to a considerable computational time.

The event-triggered approach has been utilized to deal with various control problems [18], [19]. Note that the closed-loop system subject to an event-triggered controller is a hybrid dynamical system. The most important advantage of the event-triggered direct adaptive control scheme [19], unlike other approaches (gradient, Lyapunov, etc.), is that it does not depend on the persistence of excitation condition to guarantee the convergence of parameter estimation. Through the proposed scheme, a novel regulation-triggered identifier is formulated, allowing us to use certainty-equivalence controllers without slowing adaptation. The following main ideas are implemented into the proposed control design: 1)Utilizing piecewise-constant parameter estimates between the event-based triggers. This idea omits the crucial issue of disturbing the effect of rapidly changing estimates [20], [21],and 2) The parameter estimation is regulated by error, but there is no error-based estimation leading to the parameter updating rate.

The rest of the paper is organized as follows. We derive the model of a Euler-Lagrangian system (e.g., a robot manipulator) for employing the adaptive certainty-equivalence control law using the batch least-square identifier (BaLSI)[22]. Then, we reveal that the closed-loop system is globally asymptotically stable, subject to all necessary assumptions.Finally, as a benchmark, we utilize the proposed method for a two-link robot in the presence of four uncertainties, to reveal the performance and significance of the proposed scheme.

II. PROBLEM STATEMENT

A. Mathematical Model

The nonlinear and coupled second-order differential equation for an n degrees-of-freedom manipulator is as follows,

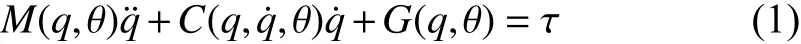
where, q ∈Rn, q˙ ∈Rn, and q¨ ∈Rnare angles, angular velocities, and angular accelerations of joints, respectively,τ ∈Rnindicates the vector of joints’ driving torques, and θ ∈Rpis the vector of system’s parameters. Also,M(q,θ)∈Rn×n, C (q,q˙,θ)∈Rn×n, and G (q,θ)∈Rnare the mass,Coriolis, and gravitational matrices, respectively, which we symbolically derived using the Euler-Lagrange equation[23]-[25]. Note that the inertia matrix M(q,θ) is symmetric,positive definite, and consequently invertible. This property is used in the subsequent development.

B. Control Objective

We control a nonlinear system having interconnected parametric uncertainties. Therefore, a highly computationally efficient adaptive controller needs to be designed guaranteeing perfect tracking. We formulate a Batch Least-Squares Identifier (BaLSI) adaptive controller along with revealing its convergence. As a case study, the controller is formulated for a robotic manipulator - one of the examples of nonlinear systems with coupled uncertainties and nonlinearities.

III. DESIGNING BALSI ADAPTIVE CONTROL LAW

In this section, we formulate the adaptive control law to efficiently estimate unknown parameters along with guaranteeing perfect tracking. We design a certaintyequivalence controller combined with the Batch Least-Squares Identifier in order to have a certainty-equivalence adaptive controller along with the event-triggered identifier.

Therefore, we need to derive the dynamic equations of the system including some parametric uncertainties, and then design the controller to stabilize the error dynamics making the origin asymptotically stable. The system (1) can be rewritten as follows,

A. Designing Certainty-Equivalence Controller

B. Batch Least-Squares Identifier (BaLSI)

C. Error System Development

The control objective includes converging joint position and velocity errors to zero implying the generalized coordinates

and the derivative of new CLF is

IV. RESULTS

We study a two-link manipulator with the following mass,Coriolis, and gravitational matrices,

where,

Fig. 1. A two-link manipulator.

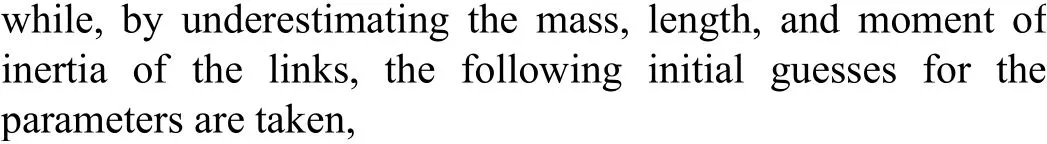
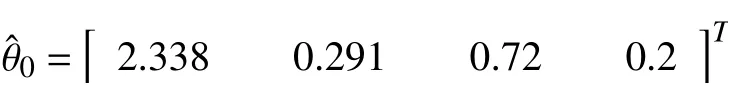
with the following initial conditions,

Here we investigate the identifier (23) with the following parameters, along with the controller, to stabilize the manipulator at the fully extended unstable equilibrium point,

As can be seen in Fig. 2, the first event-triggered parameter adaptation happens at t=1.44 s ＜T due to the dramatic growing of the Lyapunov function, although the second one happens 5 s after the first one (since T =5 s). After two estimations, the parameters converge to their actual ones, and the controller properly stabilizes the system.

Fig. 2. The parameter estimation process.

Figs. 3 and 8 present the performance of the proposed adaptive scheme and also stability of the two-link robot at the fully extended unstable equilibrium point. Fig. 8 illustrates that the tracking errors and their time derivatives asymptotically converge to zero.

Fig. 3. The joints’ angles in the case of having parameter estimation update.

Fig. 4. The control torques of the joints in the case of having parameter estimation update.

The control torques of the joints are also illustrated in Fig. 4,indicating that the system becomes stable at the equilibrium point, and the control torques converge to zero.

To demonstrate the importance of parameter estimation,both the phase portrait and value of Lyapunov function for both the cases (with and without parameter estimation) are shown.

Fig. 5 presents the phase portrait of tracking error and its time derivative for link 1 when there is an identifier along with the controller (blue line), and there is not an identifier(red dashed line). As can be seen, the trajectory with batch parameter estimation converges to zero (blue) while the trajectory without batch parameter estimation does not (red).Fig. 6 presents the phase portrait of tracking error and its time derivative for link 2, again for both the cases.

The phase portraits shown in Figs. 5 and 6 demonstrate the importance of parameter estimation in the stability of closedloop system. As expected, the phase portraits of the nominal closed-loop system asymptotically converge to the origin,although in the presence of uncertainty and without any parameter estimation, the phase portraits never converge to the origin. Figs. 5 and 6 reveal that, in the case of having parameter estimation, the phase portraits converge to the nominal closed-loop ones, after the first parameter adaptation,and then asymptotically converge to the origin. Also, the values of the Lyapunov function can be seen in Fig. 7,indicating that the inequality (11) is satisfied att=1.44s while the first parameter adaptation, as expected, happens at that time.

Fig. 5. The projection on the e1 vs. e˙1 plane solution of the closed-loop system with the proposed controller.

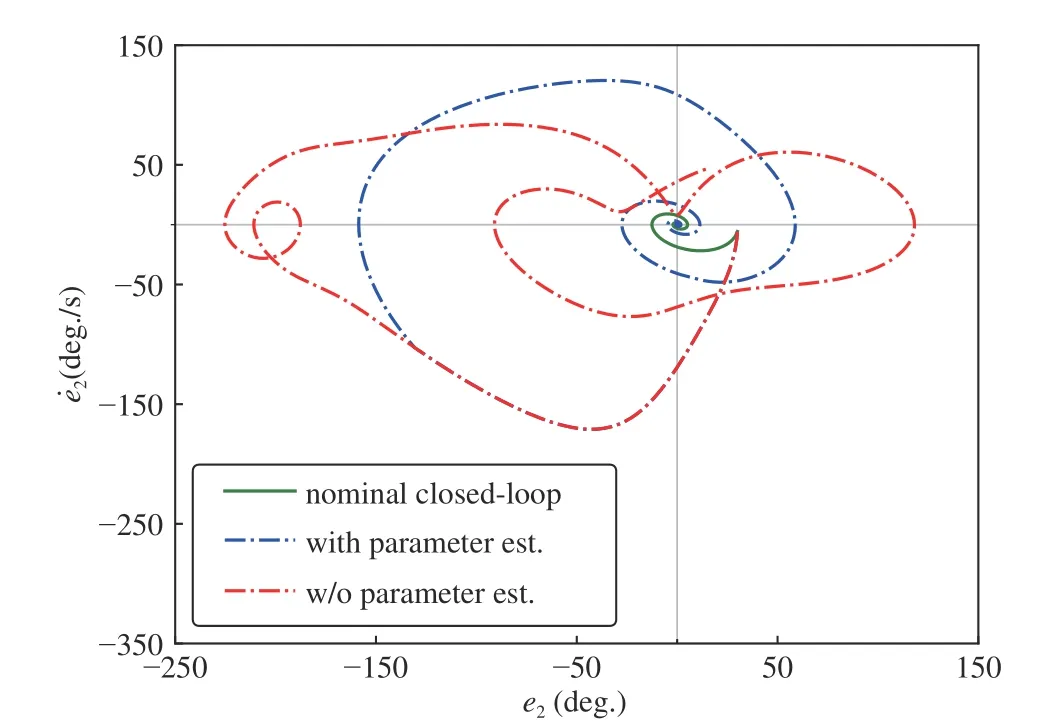
Fig. 6. The projection on the e2 vs. e˙2 plane solution of the closed-loop system with the proposed controller.

Fig. 7. The values of Lyapunov function for the closed-loop system with the proposed controller.

It is worth mentioning that, in the control law (42), selecting small α and β matrices would yield a more effective role for the model relevant part of the control scheme.

V. CONCLUSIONS

Throughout this paper, we designed a trigger-based adaptive controller for robot manipulators to estimate the unknown parameters and also to achieve asymptotic stability in the presence of uncertainties. We studied a 2-DOF manipulator(Fig. 1) with four unknown parameters and stabilized the system at the fully extended unstable equilibrium point along with efficiently estimating the unknown parameters.

To this end, we rewrote the manipulator equations in the general form of (3) and extracted the unknown parameters in addition to designing the proper nominal controller. Toward designing the controller, we formulated the proper Lyapunov candidate function using the backstepping approach and then designed the nominal controller to asymptotically stabilize the system without any uncertainties. The simulation results revealed that the controller, in the presence of parametric uncertainties, makes the robot manipulator asymptomatically stable and also efficiently estimates the unknown parameters.Fig. 8 illustrates the convergence of tracking errors and their time derivatives to zero. Also, the parameter estimation process using the proposed scheme was shown in Fig. 2.

Fig. 8. The (a) tracking errors and (b) tracking errors’ time derivatives with parameter estimation update.

ACKNOWLEDGMENT

This article is based upon work supported by the National Science Foundation under Award #1823951-1823983. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof.