Novel Stability Criteria for Linear Time-Delay Systems Using Lyapunov-Krasovskii Functionals With A Cubic Polynomial on Time-Varying Delay

Xian-Ming Zhang, Senior Member, IEEE, Qing-Long Han, Fellow, IEEE, and Xiaohua Ge, Member, IEEE

Abstract—One of challenging issues on stability analysis of time-delay systems is how to obtain a stability criterion from a matrix-valued polynomial on a time-varying delay. The first contribution of this paper is to establish a necessary and sufficient condition on a matrix-valued polynomial inequality over a certain closed interval. The degree of such a matrix-valued polynomial can be an arbitrary finite positive integer. The second contribution of this paper is to introduce a novel Lyapunov-Krasovskii functional, which includes a cubic polynomial on a time-varying delay, in stability analysis of time-delay systems.Based on the novel Lyapunov-Krasovskii functional and the necessary and sufficient condition on matrix-valued polynomial inequalities, two stability criteria are derived for two cases of the time-varying delay. A well-studied numerical example is given to show that the proposed stability criteria are of less conservativeness than some existing ones.

I. INTRODUCTION

TIME-DELAY systems have received considerable attention in the field of control during the past two decades.On the one hand, time-delay systems have found more and more applications in industrial control. For example, networked control systems [1] including active control systems for unmanned marine vehicles and offshore platforms in network environments [2], [3] can be modeled as time-delay systems.The problem of coordination and formation control of multiagent systems can be solved by employing time-delay system theory [4]. On the other hand, although it is well known that time-delays usually play the negative effects on a control system, their potential positive effects are often disclosed. It is proven that for networked harmonic oscillators,synchronization cannot be reached using current position data,but can be achieved using delayed position data [5]. For offshore platforms, by intentionally introducing a small timedelay into the feedback channel, oscillation amplitudes and control forces can be reduced significantly [3]. Therefore, timedelay systems are still an important topic to research both in theory and in practice.

II. NECESSARY AND SUFFICIENT CONDITION ON MATRIX-VALUED POLYNOMIAL INEQUALITIES

Consider the following matrix-valued polynomial described by

III. APPLICATION TO STABILITY ANALYSIS OF TIME-DELAY SYSTEMS

A. Stability Criteria for the System (14) in Case 1

To begin with, we denote

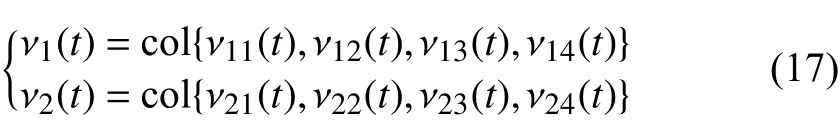
where

where

B. Stability Criteria for the System (14) in Case 2

In Case 2, since information on delay-derivative is unknown, the Lyapunov-Krasovskii functional candidate is chosen as

where

Proposition 2: For a given h¯ ＞0, the system (14) with (16)is asymptotically stable if there exist real matrices P ＞0,Q ＞0, R ＞0, symmetric real matrices Z1,Z2, real matrices Y1,Y2with appropriate dimensions and two scalars ε1andε2such that

where

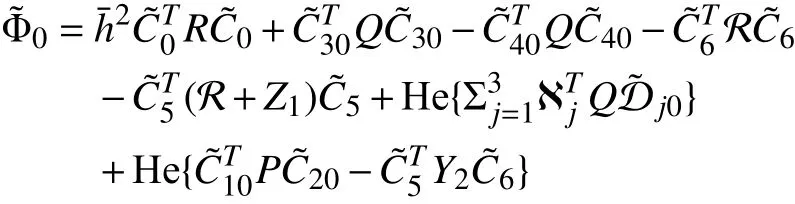
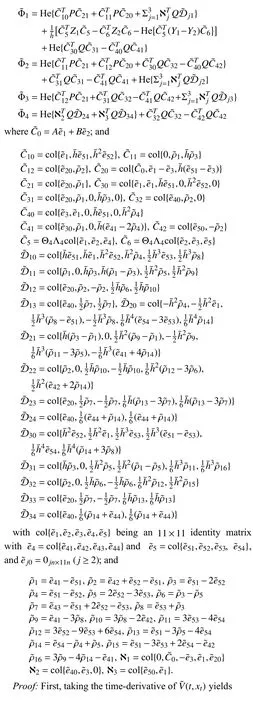
IV. NUMERICAL EXAMPLE

In this section, we take a well-studied example to compare Propositions 1 and 2 with some existing stability criteria recently reported.

Example 1: Consider the system (14) with

Case 1: Suppose that the time-varying delay satisfies (15).

In this case, we calculate the maximum admissible upper bound of h¯ for μ=-μ1=μ2∈{0.1,0.5,0.8}. Table I lists the obtained results using some existing methods [23, Theorem 1], [24, Theorem 1], [19, Theorem 8], [13, Proposition 2] and[18, Corollary 2]. However, applying Proposition 1 in this paper gives much larger upper bounds of h¯, which can be seen in Table I.

On the other hand, Table I also lists the number of decision variables (DVs) required in those methods. It is clear to see that Proposition 1 requires a larger number of DVs, which means that solving the matrix inequalities in Proposition 1 is much time-consuming. However, with the rapid development of computer technology, such a number of DVs is not a problem for high performance computers to solve the matrix inequalities in Proposition 1.

Case 2: Suppose that the time-varying delay satisfies (16).

In this case, we use Proposition 2 to compare with some existing methods [13], [25]-[27]. Table II lists both the obtained delay upper bounds and the required number of DVs by [26, Corollary 1], [27, Proposition 6], [25, Theorem 2],[13, Proposition 6] and Proposition 2 in this paper. From Table II, one can see that Proposition 2 delivers a larger upper bound h¯=3.04 than those in [13], [25]-[27]. Moreover, thenumber of DVs required in Proposition 2 is less than those of[25, Theorem 2] and [13, Proposition 6].

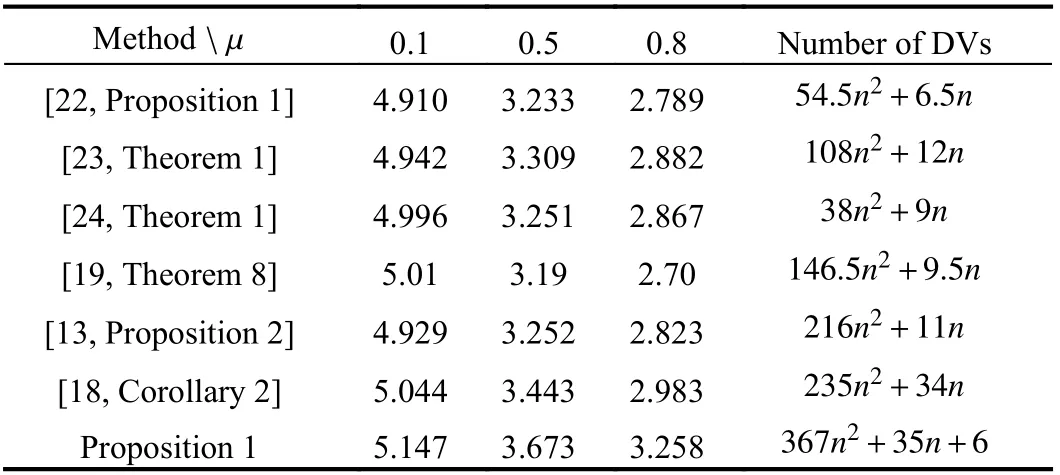
TABLE I THE MAXIMUM AD MISSIBLE UPPER BOUNDh¯ FOR DIFFERENT VALUES OF μ=-μ1=μ2

TABLE II THE MAXIMUM ADMISSIBLE UPPER BOUND h¯ FOR CASE 2

V. CONCLUSION

Stability of linear systems with a time-varying delay has been studied. First, a necessary and sufficient condition on matrix-valued polynomial inequalities has been established.Then, this condition has been employed to formulate two stability criteria for two cases of the time-varying delay,respectively, where the time-varying delay is differentiable or only continuous. Simulation has shown that the obtained stability criteria can provide larger delay upper bounds than some existing ones.