基于谱元模型的带斜坡覆水场地地震动效应分析

孔曦骏,李鸿晶

(1.南京工业大学 工程力学研究所,江苏 南京 211800;2.南京工业大学 土木工程学院,江苏 南京 211800)

涉水工程抗震设计时需要考虑地震动引起的动水压力作用,《铁路工程抗震设计规范》[1]《公路桥梁抗震设计细则》[2]《水电工程水工建筑物抗震设计规范》[3]等都对动水压力的计算做出了明确规定。目前,国内外规范中关于动水压力的计算大多是基于流体不可压缩的假设,忽略了自由液面波动的影响,本质上是将流体对固体的作用简化为固体的附加质量来进行计算[4-8]。但是上述关于动水压力的计算只是基于坝体、深水桥墩等水下结构由于地震作用而在水中运动时受到的水体压力影响,即认为水体在地震过程中始终处于静止状态。然而对于覆水场地,当地震波通过岩土介质进入水体时,特别是SV波斜入射或者P波入射情形下,水中存在透射的压缩波,这种压缩波直接或者经过水体自由表面反射后,作用于水中结构物表面,从而对结构安全性产生影响。

地震引起的动水压力可以分为3种情形:① 自由场动水压力,见图1(a);② 结构物在静水中运动产生的动水压力,见图1(b);③ 波浪作用产生的动水压力,见图1(c)。上述3种动水压力的计算过程各不相同,其中,后两种情形研究相对较多,而自由场动水压力需要基于流体和固体的波动方程进行计算,并考虑流体和固体介质之间的耦合效应,目前研究尚不充分。

图1 地震引起的动水压力Fig.1 Earthquake-induced hydrodynamic pressure

覆水场地地震动特性的研究方法主要有解析法和数值法两种。王进廷等[9-10]、Wang等[11]、李伟华等[12]和赵成刚等[13]分别给出了不同场地模型的波动解析解,解析解具有很高的理论价值,但一般只能解决简单规则地形的覆水场地问题。数值法因其能处理复杂场地问题而成为研究近场波动问题的主流方法。Maeda等[14]采用三维有限差分法模拟了带火山湖的火山场地模型,并进行了有水和无水情况下场地效应的对比分析,模拟结果表明,当入射波周期低于2 s时,水域对地震波传播具有重要影响。朱镜清等[15-16]将海水视为黏性不可压缩流体,得出了剪切波在海水与海床土一维模型中传播的差分数值解,同时考虑了海底淤泥层对海洋工程地震环境的影响。Ken[17]使用边界元法分析了Rayleigh波入射情况下,海水对近海场地地表运动的影响,研究表明,海水越深,入射波频率越高,海水对场地地震动的影响越明显。李金成等[18]采用有限元法进行了二维海底凸起地形和凹陷地形下的流固耦合计算,结果表明,海水对凸起地形下海床土的地震反应有降低作用。席仁强等[19]基于任意拉格朗日-欧拉描述,计算了海底三角形起伏场地以及沉管隧道引起的起伏场地的地震反应,结果表明,横向非均匀场地对流场影响明显。姜忻良等[20]和杨书燕等[21]研究了地震作用下河流对邻近建筑物的影响,结果表明,建筑物离河流越近,地震反应越大。Komatitsch等[22]将谱元法引入场地地震动的流固耦合分析中,采用速度势作为流体方程的未知量,形成的流-固动力方程总质量矩阵为对角阵形式,并开发了相应的显示并行计算程序SPECFEM2D与SPECFEM3D,主要分析了声波在覆水场地中的传播过程。宝鑫等[23]通过将人工边界处节点的自由场位移转化为等效荷载，提出了流体介质动力人工边界处的P波垂直输入方法，并研究了海域岛礁场地在P波垂直输入时的地震反应。杜修力等[24]研究了地震和波浪联合作用下自由场海水的动水压力变化,系统概括了地震产生的动水压力种类,结果表明,浅水的动水压力随着水深的增加而线性增加,深水的动水压力变化则与地震频率有关。

笔者在改进SPECFEM2D程序的基础上,以长江中游沙市站等水文站实测大断面为背景[25],建立了不同坡度和不同水深的带斜坡覆水场地模型,针对不同阻抗比的土层介质,从土底垂直输入不同卓越频率的平面SV波,研究了不同工况下地震引起的自由场江水动水压力变化。本文研究几何地形、水深、地震波卓越频率以及土体性质对江水地震动水压力的影响规律,并为涉水结构(如跨江大桥、过江管道等)的动水压力荷载估算提供借鉴。

1 流-固耦合谱元方程

谱元法[26-27]依据插值模式主要分为Legendre谱元法[28]和Chebyshev谱元法[29-30],其中Legendre谱元法形成的质量矩阵为对角阵形式,便于建立显式动力算法,在大型波动分析中应用广泛。借助处理流体动力方程的速度势格式[22],基于谱元法的流-固整体质量矩阵仍然保持对角阵形式,运动方程可表示为

(1)

式中:U和Φ分别为固体位移矢量和流体速度势,速度矢量V=Φ;Ms和Mf分别为固体质量矩阵和流体质量矩阵;Ds和Df分别为与固体吸收边界和流体吸收边界相关的矩阵;A为流体和固体两种介质的耦合矩阵,由交界面的位移和应力连续条件产生;Ks和Kf分别为固体刚度矩阵和流体刚度矩阵;F为固体中波源的等效荷载矢量,亦可施加于流体区域。

流体的压力p与速度势Φ的关系为

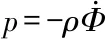
(2)

式中，ρ为流体密度。

若不考虑流体自由液面的波动,即自由液面处的压力为0,则自由液面处的边界条件可以表示为Φ=0。

流固交界面处需满足法向速度和法向力连续,即

(3)

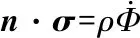
(4)

式中:n为流固交界面处法向单位向量,σ为固体介质中的应力矢量。

2 覆水场地谱元模型

选择长江流域内的覆水场地为研究对象,根据实测断面资料以及水文信息[25],得到的场地模型如图2所示。

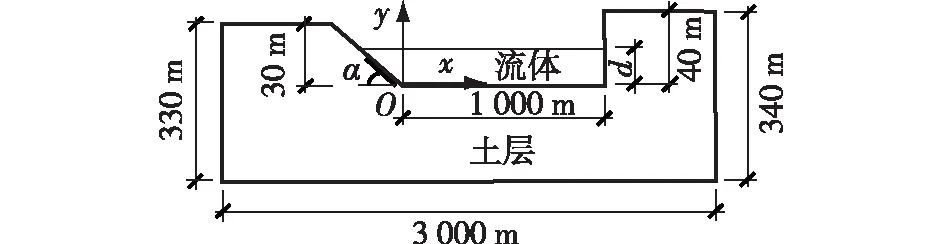
图2 带斜坡覆水场地模型Fig.2 Overlying water field model with side slope

模型中,河床及河岸岩土介质描述为均匀弹性介质,上覆河水为无黏性流体,即理想流体。河床平直,宽度取为1 000 m。一侧河岸为垂直边坡,另一侧为斜坡,与水平河床的角度呈α。两岸地表不在同一水平面上,河道深30 m。在枯水期和汛期水深有所不同,以d表示水深。几何模型以河道左侧坡脚处为原点,水平向(沿河床底部方向)为x轴,竖向(沿水深方向)为y轴。地表为自由边界,在下部、左侧和右侧弹性介质中设置人工边界,形成的计算域范围:宽3 000 m、高330～340 m。考虑软土、硬土和岩石3种介质,相应的介质参数列于表1中。

表1 介质和水的材料参数

岩土介质和水均采用谱单元模型进行离散,选择的谱单元模型为二维四边形实体单元。单元形函数为定义在Gauss Lobatto Legendre(GLL)积分节点上的拉格朗日插值函数,即勒让德函数,单元阶次取为4阶[29]。谱单元内的插值节点呈非均匀分布状态,为保证波在离散网格中的传播,单元网格的尺寸需足够小,单元网格尺寸的选取宜满足:在弹性介质中单位波长范围内平均至少有4.5个插值节点,在声学介质中单位波长范围内平均至少有5.5个插值节点。本文模型中,岩土介质单元网格尺寸为5～10 m,水体单元网格尺寸为1.5～8 m。

3 输入地震动

本文主要考察SV波垂直入射情况下覆水场地的地震动效应。为了研究SV波频谱成分的影响,选择含有不同卓越频率的Ricker波作为输入地震动。Ricker波的频谱在零频附近成分较少,能较好地避免黏性边界存在零频偏移现象。Ricker波的加速度时程及加速度幅值谱如图3所示(以卓越频率f0=5 Hz为例),函数表达式为

(5)

式中:a(t)为加速度时程函数,t为时间。

虽然地震产生的自由场动水压力和结构在水中振动产生的动水压力原理不一样,但为了便于比较两者的量级,笔者选取8度抗震设防烈度作为参考标准,加速度峰值调为0.15g(加速度最大值amax=1.47 m/s2)。需要注意的是,Ricker波函数本身是关于t=0 s轴对称的,为了完整地输入Ricker波,本文修改了模型中射波输入的起始时刻,如图3(a)所示。

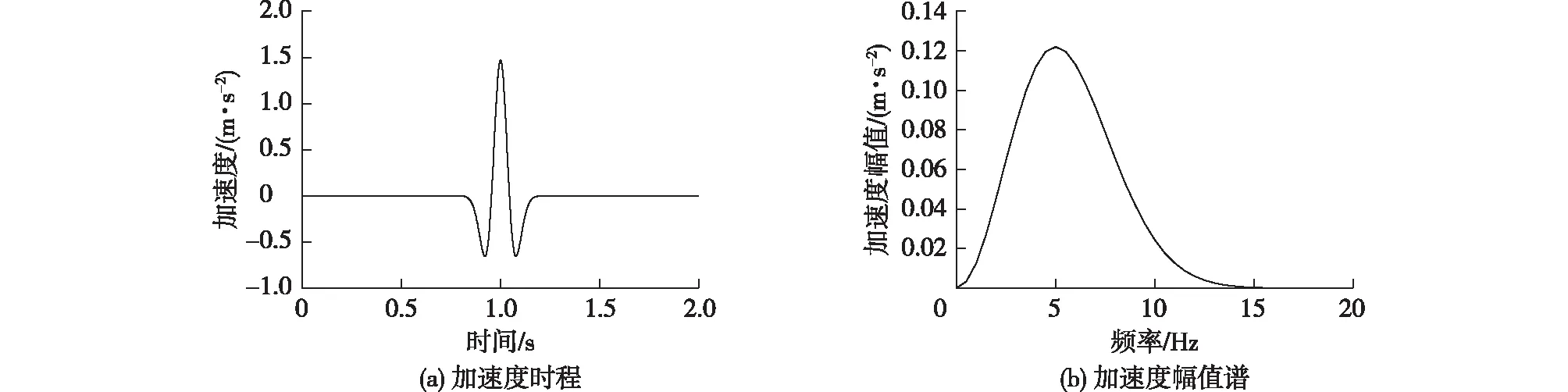
图3 Ricker波加速度时程和幅值谱 (卓越频率f0=5 Hz)Fig.3 Acceleration time history and acceleration amplitude spectrum of Ricker wave (predominant frequency f0=5 Hz)

4 动水压力计算与分析

4.1 斜坡坡度的影响

斜坡在场地地震动研究中是具有重要意义的地形之一。由于本文模型中入射的地震波为垂直向上传播的SV波,水体的波动主要来自垂直于河道两侧流固边界处的运动分量。因此,研究斜坡坡度(α)对考察河岸与水体之间地震波传播的影响程度十分有必要。图4为水深d=30 m处,不同斜坡坡度下河床表面各测点处动水压力的时程曲线。水深30 m在本模型中意味着河道充满水,即考虑长江汛期时的情况。入射Ricker波的卓越频率选取为5 Hz,处于实际地震频率的主要分布范围内。

由图4可知:地震波从河岸两侧(测点横坐标x=0 m、测点横坐标x=1 000 m)处传入水中,并在水体内来回震荡并衰减。比较图4(a)和4(f)可知,在1.2～2.0 s时,斜坡坡度为90°的模型比斜坡坡度为15°的模型整体动水压力更大,这是因为随着斜坡坡度的增大,传入水体内地震波的能量也越大,相对衰减也就越慢。

图5为不同斜坡坡度下左侧斜坡坡脚处(测点横坐标x=0 m、测点纵坐标y=0 m)的动水压力时程及峰值变化曲线,结合图4中河床表面(x=0 m)处的动水压力时程曲线,可以发现：斜坡坡度越大,斜坡坡脚处的动水压力越大,其峰值与斜坡坡度大致呈线性正相关关系。

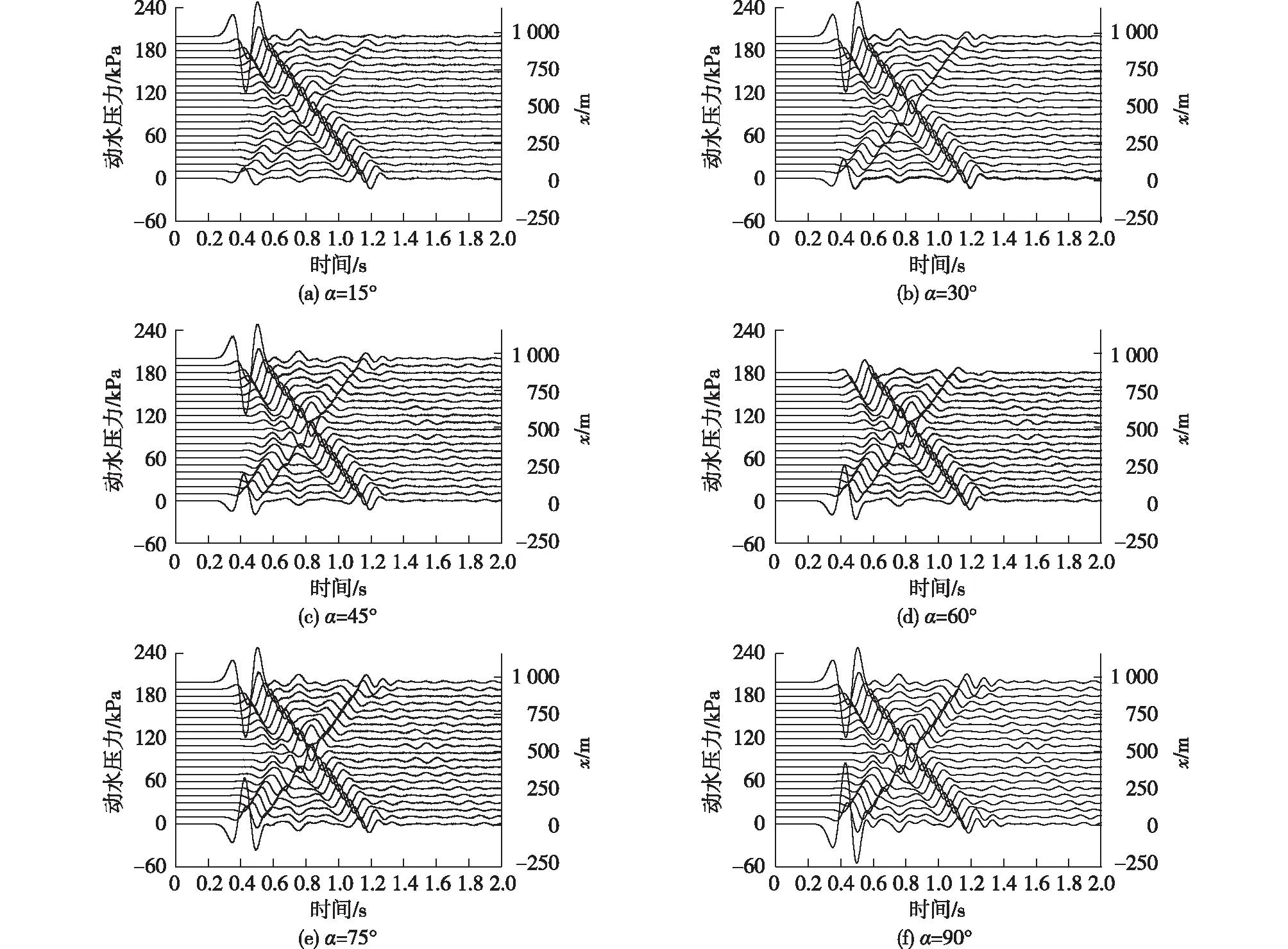
图4 不同斜坡坡度下河床表面各测点处动水压力时程曲线(f0=5 Hz、d=30 m)Fig.4 Time history curves of hydrodynamic pressures on the surface of river bed under different side slopes (f0=5 Hz,d=30 m)

图5 不同斜坡坡度下坡脚处动水压力时程和动水压力峰值(x=0 m、y=0 m)Fig.5 Time history of hydrodynamic pressures and peak values at the toe of slope under different side slopes (x=0 m,y=0 m)

图6(a)和6(b)分别为河床表面和河中横向各测点的动水压力峰值。由图6(a)和6(b)可知:河道中间部分各测点(远离两侧坡脚50 m范围外,即图6(a)中红色框内测点)动水压力比较接近且受斜坡坡度影响较小,而河道两侧附近的动水压力相对河道中间部分的动水压力明显更大,且斜坡越陡,河岸附近的动水压力越大。图6(c)和6(d)分别为x=0和50 m沿y轴方向各测点的动水压力峰值。由于纵坐标正向是由河床指向河水表面，因此y的大小与测点距离河水表面的距离(即水深)是线性负相关的，y的减小即意味着水深的增加。由图6(c)和6(d)可以看出:动水压力峰值随水深的增加而增大,斜坡坡度≤60°时,动水压力随水深增加而表现为线性增大,而斜坡坡度>60°时,坡脚处(x=0 m)的动水压力峰值随着水深增加呈抛物线型增大,增大趋势渐缓。

图6 不同斜坡坡度下各测点动水压力峰值Fig.6 Peak hydrodynamic pressures of the field under different side slopes

为了便于比较,取河床表面远离两岸坡脚50 m以上各测点的动水压力峰值平均值(17.08 kPa)为基准,得出不同斜坡坡度下河床表面各测点的动水压力相对放大系数β(表2)。由图6及表2知:河床右侧1 000 m(x=1 000 m)处的动水压力相对放大系数约为基准值的4.6倍,距离右侧垂直岸壁50 m(x=950 m)处的动水压力放大系数约为基准值的1.4倍,河床左侧坡脚(x=0 m)及河床靠近中间部位(x=450和550 m)的动水压力随着斜坡坡度的增大而增大,左侧坡脚β最大值为5.05,河道中间50 m范围内β最大值为1.41。由于河道两侧地震波同时到达河道中间(x=500 m)时,应力相互抵消一部分,各测点的动水压力随着斜坡坡度的增大而减小,β从0.74减小至0.48。

4.2 水深的影响

长江一年四季水深不是恒定的,与枯水期和汛期有关,且长江上下游各段水深差异比较大,深水段达到近百米,浅水段仅为几米。本文参照长江中游沙市站等水文站的调查数据[25],考察的水深工况为10、20和30 m,其中,30 m为河道满水的极限情况,10和20 m分别为常水位和普通汛期水位,此处同样设定入射波卓越频率为5 Hz。

图7为3种斜坡坡度下(α=15°、45°和90°)河床表面各测点动水压力峰值曲线。由图7可以看出:水深越大,河床表面动水压力峰值越大。表3为不同水深下河床表面各测点的动水压力峰值。表4为不同斜坡坡度下河床表面各测点动水压力峰值的比例系数。由表3和表4可知：当水深从10 m增大到20 m时,各测点动水压力峰值增大了约2倍,当水深从10 m增长到30 m时,动水压力峰值则增大了约3.5倍。

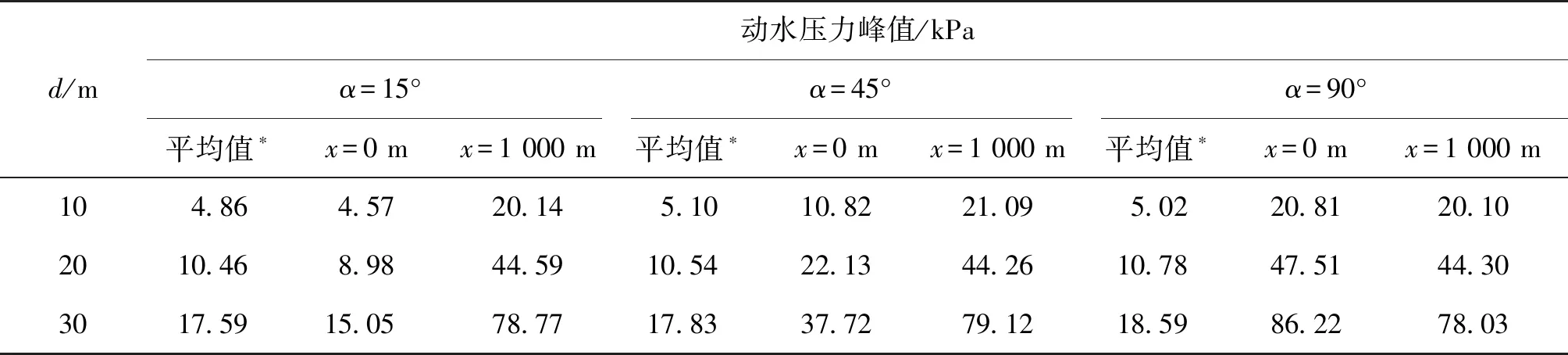
表3 不同水深下河床表面各测点动水压力峰值

表4 不同斜坡坡度下河床表面各测点动水压力峰值的比例系数

4.3 地震波卓越频率的影响

为了研究地震波卓越频率对覆水场地动水压力的影响,假设Ricker波的卓越频率取值范围为1～20 Hz,模型的水深选取为30 m,斜坡坡度设定为45°。图8为不同卓越频率的Ricker波输入时,河床表面各测点的动水压力峰值。由图8可以看出:河道两侧附近的动水压力峰值相对河道中间部分的动水压力明显更大,且在低频Ricker波输入情况下更为明显。图9为河床表面不同位置的测点动水压力峰值与入射波卓越频率之间的关系。由图9可以看出:各测点对卓越频率为1 Hz的入射波反应比较强烈,河岸两侧(x=0、1 000 m)尤其明显,动水压力峰值分别达到57 kPa (x=0 m)和104 kPa (x=1 000 m)。除河岸两侧外,各测点的动水压力在卓越频率为2 Hz时最小,然后随着卓越频率的提高而变大,在卓越频率8 Hz左右达到另一个极大值后逐渐衰减并平稳。综上所述,河岸两侧的动水压力对低频地震波的输入十分敏感,而河床表面远离岸边的动水压力则对卓越频率为1或7～9 Hz时的地震波输入比较敏感。

图8 不同卓越频率的Ricker波输入下河床表面各测点动水压力峰值(α=45°、d=30 m)Fig.8 Peak hydrodynamic pressures on the river bed surface due to Ricker waves with different predominant frequencies(α=45°, d=30 m)

图9 河床表面不同位置处动水压力峰值与卓越频率的关系Fig.9 Relationship between peak hydrodynamic pressures and predominant frequency on the river bed surface

4.4 土体介质的影响

弹性波在不同介质交界面的传播需要满足位移和应力连续条件,一维波在界面上的反射和透射则完全取决于两侧介质的阻抗之比。图10为3种土层介质下,河床表面各测点的动水压力峰值曲线。表5为河岸两侧的动水压力峰值及河床中间各测点的动水压力峰值平均值。由图10和表5可以看出:土层的阻抗越大,波传入水中的透射系数越大,传递的能量越高,水体的动水压力峰值也就越大。

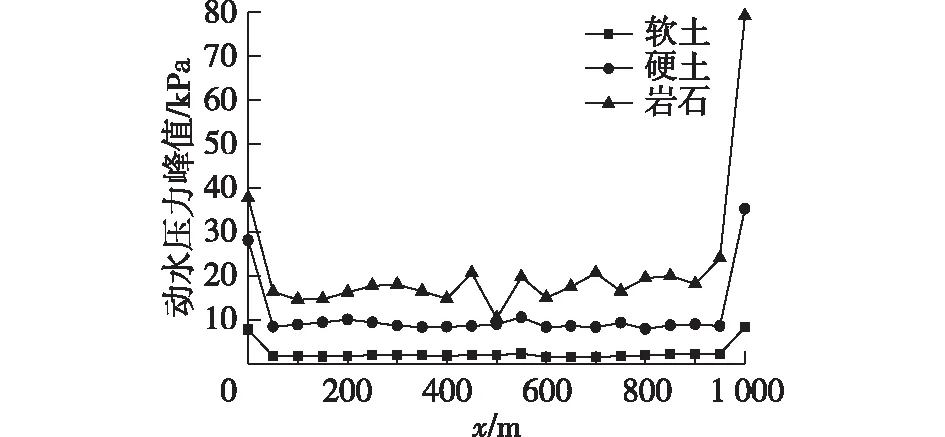
图10 不同土层介质下河床表面各测点动水压力峰值(α=45°、d=30 m)Fig.10 Peak hydrodynamic pressures on the river bed surface under different soil types(α=45°, d=30 m)

表5 不同土层介质下河岸两侧及河床中间动水压力峰值

5 结论

1)斜坡坡度对河岸附近水体的动水压力有明显影响:坡度越大,河岸附近水体的动水压力越大,河岸坡脚处的动水压力峰值与坡度大致呈线性正相关关系。远离河岸50 m以上的动水压力几乎不受斜坡坡度影响,但河道中间部分附近的动水压力会随斜坡坡度发生小幅度变化。因此,桥墩设置在河岸坡脚附近时,宜重视动水压力的作用及其带来的影响。

2)水深对河床表面动水压力有明显影响。水越深,动水压力越大,水深30 m时河床表面的动水压力是水深10 m时相同位置动水压力的3.5倍左右。考虑到长江等水系水深会因为枯水期和汛期而发生变动,河床表面的动水压力宜按照河道满水情况来进行保守计算。

3)入射地震波的卓越频率对水体动水压力影响显著。河岸附近水体的动水压力对低频地震波十分敏感,河道远离岸边水体的动水压力则对卓越频率为1或7～9 Hz时的地震波比较敏感。

4)土体介质的阻抗越大,传入水体内的地震波能量也越大。笔者假设土体为单一均匀介质,考虑到实际场地介质的复杂性,土体介质对地震作用下江河水体内的动水压力影响值得进一步研究。