基于权重搜索树改进K近邻的高维分类算法
2021-04-13梁淑蓉陈基漓谢晓兰
梁淑蓉, 陈基漓,2*, 谢晓兰,2
(1.桂林理工大学信息科学与工程学院, 桂林 514004; 2.广西嵌入式技术与智能系统重点实验室, 桂林 514004)
技术的发展促使数据集凸显规模和复杂性,与低维数据相比,高维空间中不同数据之间的相似性概念变得模糊,因此对高维数据的挖掘,机器学习方法将面临严峻考验。一方面,根据数据索引构造的数据挖掘性能减退;另一方面,根据距离度量函数的全维度挖掘失去效果。例如:在高维空间中的K近邻分类算法(Knearest neighbors,KNN),由于数据之间距离的概念不复存在,距待分类数据的最近点和最远点之间的距离几乎相等,使得最近邻计算无法区分最近邻域。如何提高算法的效率是高维数据分类面临的挑战。
针对这一问题,许多学者对高维空间中维数灾难问题开展研究。一类研究通过降维技术去除冗余信息,来实现减少计算量和时间的目的。李勇等[1]提出一种通过可变K近邻局部线性嵌入(locally linear embedding,LLE)降低数据维度的方法,使得即使在维数减小后的特征向量情况下,也可以在高维空间中保留拓扑结构并实现高检索精度。万静等[2]为了降低不确定数据对聚类产生的影响,将数据划分为值不确定和维数不确定,并采用期望公式度量距离,再通过K近邻查询来找寻不确定数据的近似值,此算法具有良好的抗噪声特性和可伸缩性。还有一些研究通过对特征属性进行加权,“忽略”某些属性以实现降维的效果。为了提高高维数据中KNN分类的准确性,Zhu等[3]提出了一种新的KNN方法,该方法实现高维数据的属性选择和属性权重加权,能消除不相关属性并获得原始预测属性的表达式。李金孟等[4]提出一种HWNN算法,用于高维不平衡数据的维度灾难和类不平衡分布的问题,通过类加权方法增加少数类在所有样本中的分布系数,在普通维度的不平衡数据中,该算法的预测精度也很显著。Hadi等[5]在初始阶段使用平滑修剪的绝对偏差(smooth integration of counting and absolute deviation,SCAD)Logistic回归,同时构建每个特征在相异度度量的重要性,并使用特征贡献作为欧几里德距离中SCAD系数的函数,该方法能消除几乎所有非信息性特征,在准确性和降维方面均具有良好的性能。
以上方法均从如何降低维度进行研究,未考虑距离计算公式的优劣对高维数据的影响。一类研究则是通过优化距离计算方式来提高分类效率,雷宇曜等[6]提出一种归一化函数,在演化过程中对密度函数应用了Minkowski距离差“K近邻”的方法,以加快算法收敛速度,其性能相对其他算法具有优势。Huang等[7]提出了一种基于自适应簇距离限制的改进的KNN搜索算法,该算法通过减少处理器成本来实现高维索引,使用三角形不等式滤除不必要的距离计算而实现,但该算法预处理成本较高。Wang[8]提出一种算法,这种算法使用聚类和三角形不等式减少距离的计算,加速高维空间中近邻搜索,将距离计算减少2~80倍,并将速度提高了2~60倍。
综上,高维数据不仅使数据挖掘呈现“维度灾难”,同时常用的欧式距离公式不能很好地面对日渐增长的数据规模。为了解决这些问题,本文提出基于权重搜索树改进K-近邻(K-nearest neighbor algorithm based on weight search tree, KNN-WST)的高维分类算法,需先根据数据集属性按一定规则构造搜索树,把数据按搜索树划分成不同的矩阵区域,树的叶子结点存储对应矩阵区域数据的索引,其中由于矩阵区域所包含的数据都经过相同分支路径,因此这些数据之间互为相似。当需要对未知样本进行分类时,未知样本查找搜索树可以得到与其最为接近的叶子节点,并只与存储在该叶子结点的索引映射数据计算相似性。简言之,仅计算未知样本与查找搜索树所获数据之间距离。一方面针对高维数据中数据之间距离的概念变得模糊,分类效率下降的情况,研究和讨论适合高维数据的距离计算方式。另一方面针对高维数据“维灾”的特征,引入树形结构,利用部分特征属性按一定规则构造搜索树,将高维数据划分为不同的矩阵区域,分类仅与一个矩阵区域内数据距离度量,减少距离比较次数,从而达到降维和提高KNN算法在高维数据中分类效率的目的。
1 相关研究
Cover等[9]提出的KNN算法是最简单、最高效的机器学习算法之一,在实践应用中发挥着积极的作用[10-12]。该算法是一种惰性学习,即在分类过程中没有训练的阶段,数据集事先已知分类类别和特征属性,需要分类的未知样本直接进行分类处理。
该模型结构简单且易于理解,通常无需多个参数即可获得良好的性能。许多研究者对KNN算法的改进方法及应用方向仍保持热忱。例如:齐斌等[13]改进了表示KNN加权局部线性文本特征的方法,对表示系数进行加权使其稀疏,并引入非负约束来避免噪声对表示系数的干扰。李峰等[14]将标签空间划分为几个颗粒状标签,计算每个标签的权重系数,解决了算法忽略标签之间相关性的问题。朱利等[15]提出了一种基于K-d树的近似KNN空间聚类算法,利用K-d树的数据结构进行空间聚类,具有更好的性能。但这些改进方式未能考虑高维数据的影响,不能很好地适应当今大数据分析能力的要求。
1.1 KNN算法基本概念
KNN分类算法的核心思想是判断数据之间距离的大小,距离越近则两数据之间的相似性越大。具体的实现步骤为:通过未知样本与数据之间的距离计算,在最接近未知样本的k个“最近邻”中找到最常出现的类别,这个类别为未知样本经过分类得到的类别。实现具体形式如算法1介绍。
算法1 KNN algorithm
输入:训练数据集t_Set,未知样本test_Data,k。
输出:未知样本的分类类别。
(1)数据归一化。
(2)计算未知样本test_Data与t_Set之间的距离D, {d1,d2,…,di}∈D,i=1,2,…,t_Set.num。
(3)D按距离递增次序排序。
(4)选取与未知样本距离最小的k个点。
(5)计算这k个点所在类别出现的频率。
(6)返回出现频率最高的类别作为未知样本的分类类别。
从算法1可发现,KNN算法对未知样本分类时,需与数据集中的每个数据样本进行距离计算,对于一个D维数据集,计算复杂度和数据集中的数量N成正比,则时间复杂度为O(DN2)。因此当分类遇到大规模或高维数据的数据集时,容易发生维度爆炸,算法分类效率大大降低。
1.2 距离度量方式
欧氏距离是一种常用的距离度量方式,随着数据集维度的增长,欧氏距离已无法高效地度量全空间相似性[16-17]。通过论述不同距离公式,包括曼哈顿距离、欧氏距离和切比雪夫距离,实验验证何种方式更适合在高维数据中度量相似性距离。
闵氏距离最早由Minkowski提出,且闵氏距离与特征属性的量纲有关,设n维空间中有两点坐标x、y,闵氏距离定义为
(1)
式(1)中:xu、yu为u(u=1,2,…,n)维空间中的两点坐标;p为常数,不同的p分别代表不同的度量方式,具体表示为
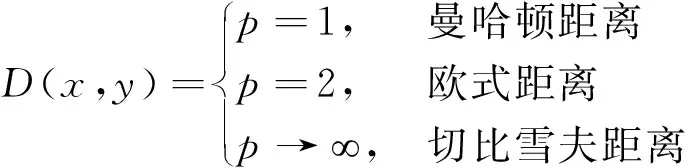
(2)
2 KNN优化算法
2.1 建立搜索树
树形结构具备三大特点:强直观、数据存储低冗余和高效遍历,在大量数据处理方面优势更为突出。搜索树的建立是一个自上而下的过程,根据数据集特征属性的权重以及一定分支规则对数据空间划分,构成一系列不同的矩阵区域,称这些区域为训练数据集的粗略簇,此时粗略簇内的数据相互之间都是“相似”的。
构建搜索树模型方法如下。
步骤1在有n维特征属性的维数据集中,使用熵权法计算特征属性权重。

步骤3将影响因子集结点按序取出作为结点node建树,使用三等分法得到每个属性包含数据的左中值Lmid和右中值Rmid两个划分阈值,根据两阈值作为分支条件,生成3个分支。
步骤4根据步骤3 的分支规则,将影响因子集中每个结点都作为一个父节点,与3个分支构成一棵子树,直至完毕。
步骤5将步骤4中生成的子树按影响因子集中原结点顺序排序。
步骤6排序好的子树逐一取出建树,第1棵子树的父结点放在第0层,作为搜索树的根结点,因根结点有3条分支,即第1层结点数为3,且均为第2棵子树的父结点。以此类推,第i层结点对应第i+1棵子树的父结点,直到n/3棵子树均被取出。
其中,作为一种客观加权法,熵权法可以确定指标的权重,剔除对评价结果无明显贡献的指标。对于一项数据样本,由于样本中每个特征属性与同一类别中的其他特征属性相比,其作用和影响力各不相同,从而对样本分类的贡献值也不同。故认为,权重值越大的特征属性,对于数据的重要性越高,越能决定数据的类别。对于包含m个样本,n个特征数的数据集,形成初始数据矩阵R=(rij)m×n,其中rij为第j个特征下第i个样本的评价值。其特征属性权重计算方法如下。
(1)计算第j个特征下第i个样本的指标值比重pij,公式为
(3)
(2)根据第j个特征的比重pij计算其熵值ej,公式为
(4)
(3)可得第j个特征的熵权wj,即第j个特征的权重,表示为
(5)
2.2 初始化搜索树
初始化搜索树的过程即对数据划分过程,训练数据从搜索树的根结点root进入,根据每个结点node不同的分支条件,将训练数据划分到不同矩阵区域。
其中,每个结点node记录经过结点的数据索引并传到与之连接的下一结点中,直到数据到达最高层叶子结点,最高层叶子结点记录数据集由搜索树划分后属于该矩阵区域的数据索引,搜索树结构如图1所示。

图1 搜索树模型结构Fig.1 Search tree model structure
对一个有n个特征属性的数据集,取n/3项属性构建搜索树,此时树的每层结点均为同一特征属性结点,第l层的结点数量为3l[l∈(0,1,…,n/3)]个。初始化搜索树的过程是将数据集按搜索树的分支规则划分为不同的矩阵区域,矩阵区域内数据索引I存储在相应的叶子结点中,此时的矩阵区域称为数据集经过搜索树划分出的粗略簇。
2.3 KNN-WST算法
2.3.1 KNN-WST算法基本概念
针对高维数据对智能算法造成的短板,提出的KNN-WST算法利用树形结构改进KNN算法,此改进达到了降维的目的,加速了最近邻的确定,从而减少了KNN算法分类时距离的计算次数。
KNN-WST算法对KNN算法优化过程具体表现在如下三个方面。
(1)预处理阶段,将数据样本集通过上述建树、初始化搜索树两步骤,划分出一系列不同的矩阵区域,此时的矩阵区域可视为训练数据集的粗略簇。
(2)在查找阶段,依据未知样本特征属性查找搜索树,得到的粗略簇视为与之最相似的相似簇。
(3)最后的分类阶段,将待未知本与相似簇中的数据进行相似性计算,从而得到未知样本的预测分类结果。
2.3.2 KNN-WST算法流程
KNN-WST算法的伪代码如算法2所示,其流程图由图2给出。

图2 KNN-WST算法流程图Fig.2 KNN-WST algorithm flow chart
算法2 KNN-WST algorithm
输入:训练数据集t_Set,未知样本test_Data,k。
输出:未知样本的分类类别。
预处理阶段
(1) 利用训练数据集t_Set特征向量构建搜索树s_tree。
(2) 将训练数据集t_Set对s_tree进行初始化。
查找阶段
(3) 查找未知样本test_Data经过s_tree分支规则得到的叶子结点。
(4) 对照叶子结点存储的索引取出t_Set中数据样本,构成一个相似簇s_Clusters。
分类阶段
(5) ifs_Clusters.num=1。
(6) then 未知样本test_Data分类结果与s_Clusters中数据类型一致。
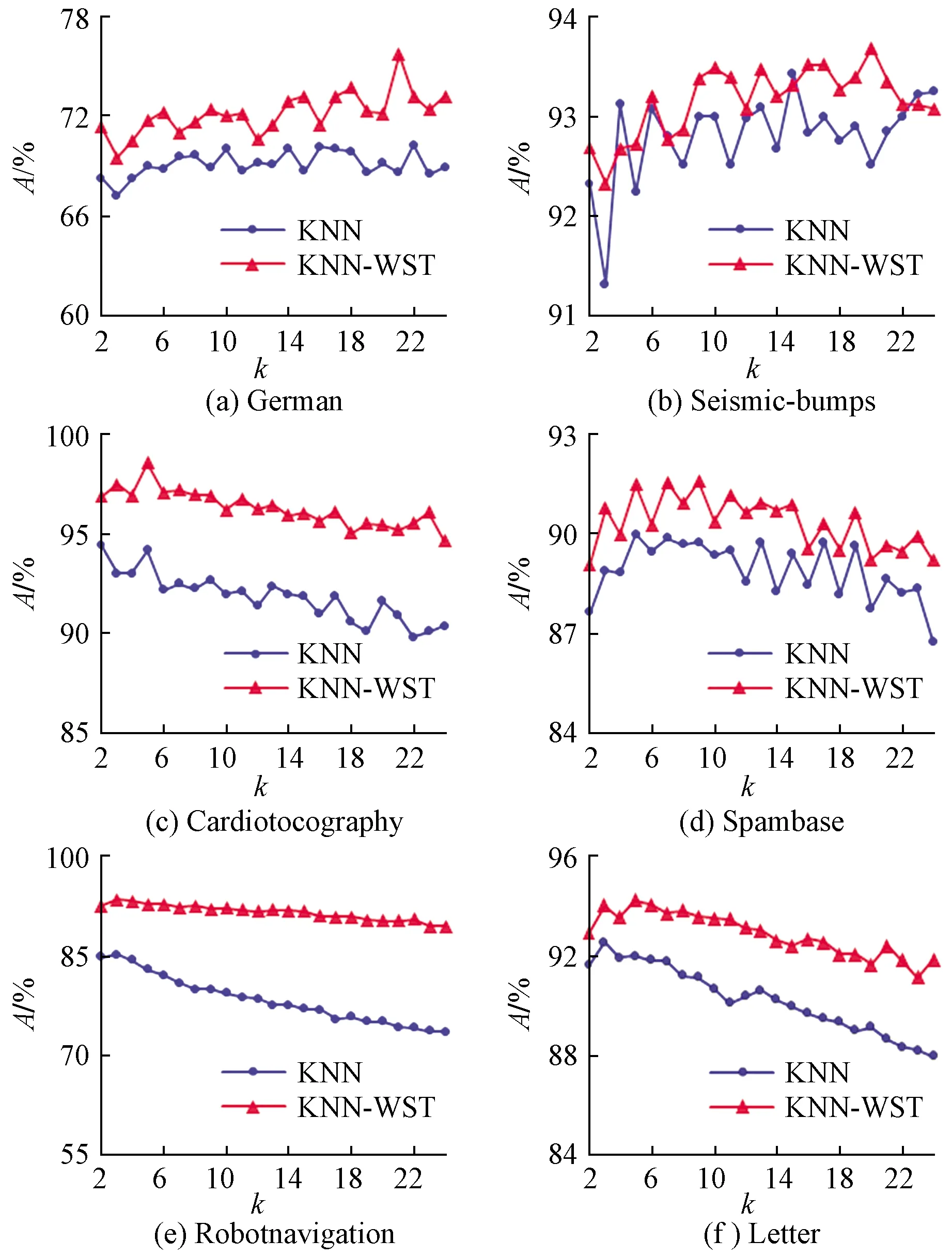
(7) else ifs_Clusters.num (8) thenk=s_Clusters.num。 (9) end if。 (10) 根据算法1计算test_Data与s_Clusters内点之间的相似性,得到test_Data分类类别。 算法的实现通过对训练数据集进行属性权重计算,根据占权重值最大的1/3项属性构建搜索树,并对此搜索树初始化,此时搜索树中叶子结点存储索引所对应数据构成了许多粗略簇,粗略簇中数据互为“相似”。当未知样本分类时,将通过搜索树查找“相似”于未知样本的粗略簇,由于未知样本和粗略簇所经过的划分规则一致,可视未知样本与粗略簇中的数据最为相似,此时粗略簇又可称为相似簇。分类计算需判断相似簇中数据数量,特别的是当仅有一个数据时,则认为未知样本与该数据同类,该数据的类别即为未知样本的预测类别;或当数据数量小于预设k时,需将k更新后再度量距离。因为经过搜索树的划分,未知样本与对应相似簇内数据具有较高的相似性,所以能在缩小计算规模的同时保证分类的准确率。 在仿真实验中,实验环境为:Windows 7操作系统,1.50 GHz CPU,8 GB内存,通过MATLAB仿真验证算法。从UCI数据集中选择了11个标准数据集进行模拟,分别验证本文算法的有效性。同时为提高模型的泛化能力,实验使用留出法按3∶7对数据集随机划分为测试集和训练集。数据集基本信息如表1所示,其中前5个数据集Haberman、Heart、Cancer、Vehicle、Ionosphere为低维数据集,后6个数据集German、Seismic-bumps、Cardiotocography、Spambase、Robotnavigation、Letter为高维数据集。 表1 数据集基本信息Table 1 Basic information of datasets 主要采用分类计算损耗时间(T)和准确率(A)两个指标评估算法性能,分类计算损耗时间T为从开始分类到最终得出未知样本的类别所消耗的时间,准确率A指全部测试样本使用算法自动分类的结果同人工分类结果一致的比率。A计算表达式为 (4) 式(4)中:TP为正确分类的正例数目;TN为正确分类的负例数目。 由于在高维数据中,数据之间距离的概念变得模糊,欧式距离不能很好应对维灾的挑战,所以对闵式距离进行实验讨论。通过对曼哈顿距离、欧氏距离和切比雪夫距离三种距离计算方式结合KNN算法,仿真采用准确率Acc评价不同距离公式的优劣性,仿真结果如表2所示。 表2为k取2~24时,不同度量方式得到的最优分类准确率,通过表2比较可得出如下结论。 表2 不同距离度量公式分类准确率Table 2 Classification accuracy of different distance measurement formulas (1)在数据集特征属性和实例数都少的情况下,3种距离度量方式计算出的结果近似,其中欧氏距离在3个低维数据集中表现良好,曼哈顿距离和切比雪夫距离只在一个低维数据中具有较好的分类准确率。 (2)随着数据维数增高,在实例数达到千量级以上的6个高维数据集中,曼哈顿距离度量方式在5个高维数据集中表现最好,欧式距离只在一个高维数据中略微优于曼哈顿距离,切比雪夫公式计算结果最差。因此,相比常用的欧氏距离,曼哈顿距离更适合度量在高维数据中度量数据之间的距离。 KNN-WST算法相较KNN算法引入树形结构,把数据集划分成不同的矩阵区域,可以大幅减少数据规模,降低时间复杂度。为了验证假设,对KNN-WST算法与KNN算法在6个高维数据集开展对比实验,其中经3.3节可知,曼哈顿距离度量方式更适用于高维数据,因此以下实验中KNN-WST算法和KNN算法均使用曼哈顿计算距离。 表3为不同k下,KNN算法和KNN-WST算法在6个高维数据集中分类计算损耗时间T,可以观察到KNN-WST算法比KNN算法平均损耗时间T上最少降低了12.7%,最多降低了80.1%。改进后的KNN-WST算法降低了数据集维度,计算复杂度下降,分类时间得到大幅优化。 表3 KNN算法和KNN-WST算法在不同k值下分类所需时间对比Table 3 Comparison of the T required for classification under different k value in case of KNN and KNN-WST 图3显示了k为2~24时,KNN算法和KNN-WST算法分别在6个高维数据集上分类准确率的详细数据。KNN-WST算法较KNN算法分类准确率都有所提高,依次提高7.67%、0.28%、4.42%、1.77%、9.80%、1.82%,从一定程度上提高了KNN算法的准确率。 图3 KNN算法和KNN-WST算法在6个数据集上的分类准确率Fig.3 Classification accuracy of KNN and KNN-WST on six datasets 同时,为了进一步验证提出算法的有效性,KNN-WST算法还同经典的分类算法:决策树和支持向量机(support vector machine,SVM)在6个标准高维数据集中进行比较,比较各类算法分类损耗时间和分类准确率,4种算法对比试验数据如表4所示。 表4 4种算法对比试验数据Table 4 Comparison test data of four algorithms 表4显示了KNN-WST算法与KNN算法、决策树、SVM算法的对比实验结果,从实验数据来看:KNN-WST算法在时间开销和分类准确率都优于KNN算法和决策树;对比公认适合处理高维特征的SVM算法,KNN-WST的分类准确率与其不相上下,在5个数据集中表现最优,SVM算法在3个数据集中准确率最高,并且由于SVM算法需对参数寻优,在分类时间开销上远远大于KNN-WST算法,因此KNN-WST算法较优于SVM算法。 通过以上仿真可知:随着数据集规模的增大,曼哈顿距离度量方式相对于常用的欧氏距离更适合在高维数据中计算相似性。同时通过仿真证明,KNN-WST算法能在略微提高分类准确率的情况下,大幅优化分类的时间开销,减少计算能耗,为今后高维数据分类的相关问题提供一定的参考。 针对KNN算法在高维数据环境下分类存在占用资源高、计算量大等缺陷,提出KNN-WST算法:利用数据集特征属性权重按一定规则构建搜索树,使数据集划分成不同的矩阵区域,未知样本只与“相似”的矩阵区域计算距离,减小未知样本与数据计算规模从而达到优化。其优点在于采用树形结构减少数据规模,距离计算次数大幅减少,使得分类的时间开销减少,同时分类准确率也有所提高。同时也讨论了在高维环境下,不同距离度量公式的优劣,得出曼哈顿距离更适合在高维数据中使用。基于KNN-WST算法设计更优改进算法,对矩阵区域中数据量唯一时,未知样本分类结果如何确定可作为下一步研究方向。3 仿真实验
3.1 数据集信息

3.2 评价指标
3.3 最优距离计算公式仿真

3.4 KNN-WST算法仿真


4 结论
