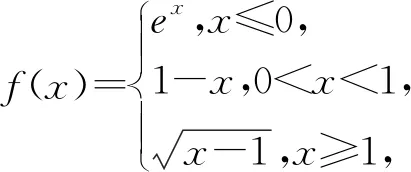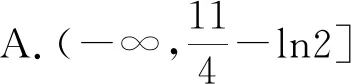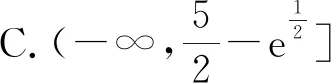函数等高线的妙用
2021-04-13江西省吉安市白鹭洲中学343000尹丙武
中学数学研究(江西) 2021年4期
江西省吉安市白鹭洲中学 (343000) 尹丙武
我们知道,地理中“等高线”指地形图上高程相等的相邻各点所连成的闭合曲线.借助于这一名词,数学中对于函数y=f(x),若存在互不相等的实数a,b,c,使f(a)=f(b)=f(c)=t,则y=t称作函数y=f(x)的等高线.利用函数的等高线求解与交点横坐标有关式子的取值范围问题综合性较强,难度也较大,一般作为客观题压轴题出现.本文就此类问题的破解方法予以总结.
1.利用对称性求解等高线对应的交点横坐标之和
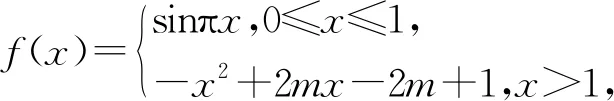
x3+x4的取值范围是( ).
A.(2,5] B.(-∞,0]∪[5,+∞)
C.[5,+∞) D.(2,+∞)
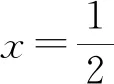
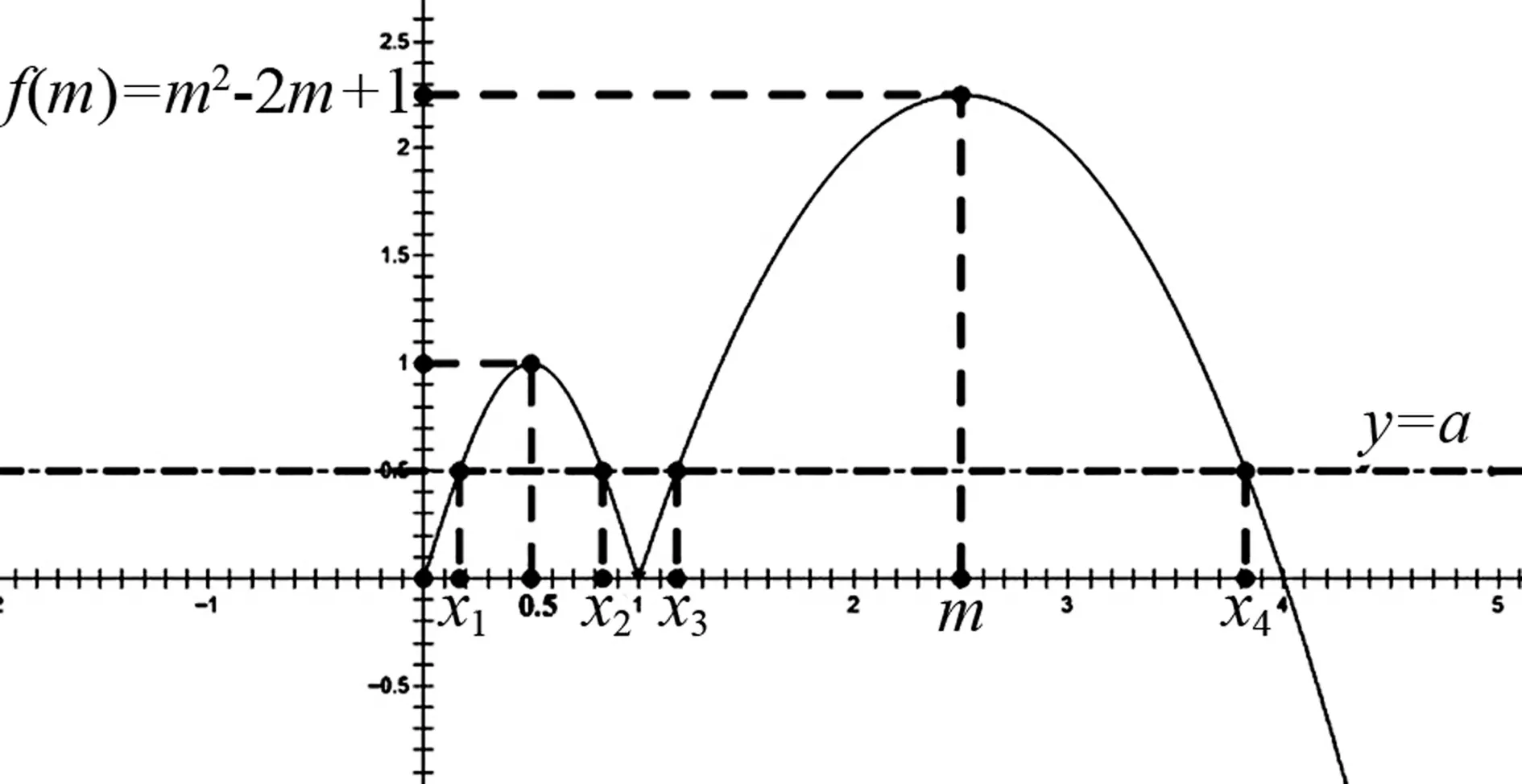
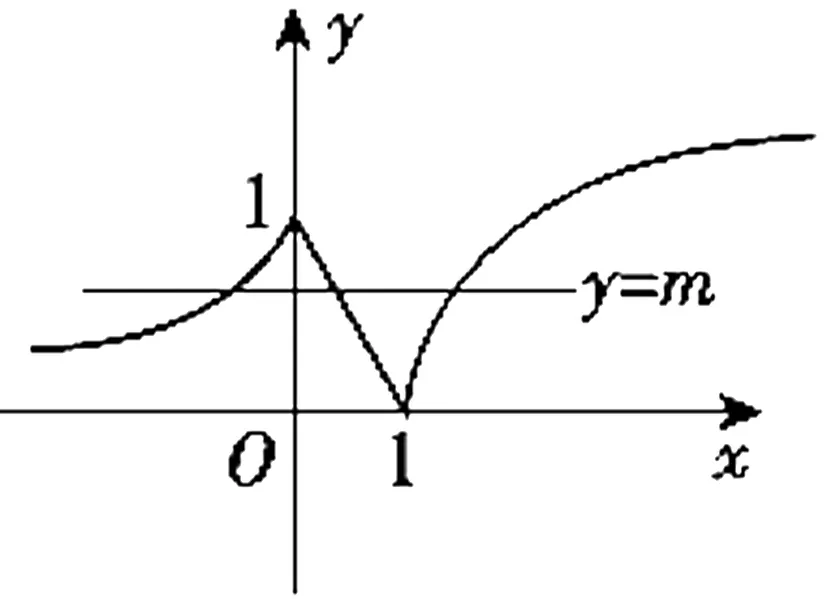
图1
评注:本题关键用两次对称性,由性质“若A(x1,y1),B(x2,y2)关于直线x=a对称,则x1+x2=2a”得出其中两个交点横坐标之和为常数x1+x2=1,另两交点横坐标之和x3+x4=2m.再结合图像确定m≥2,由此以m为主元,求出m的取值范围.
2.利用对称性求解等高线对应的交点横坐标之积
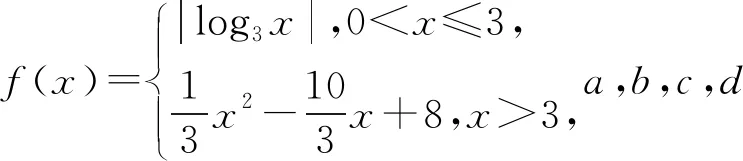
A.(18,28) B.(18,25) C.(20,25) D.(21,24)
解析:不妨设a 图2 评注:本题关键用两次对称性,由性质“若直线y=m与函数y=|logax|(a>0且a≠1)有两个不同交点A(x1,y1),B(x2,y2),则|logax1|=|logax2|,所以-logax1=logax2,x1x2=1.”得出其中两个交点横坐标之积为常数,即ab=1;另两交点横坐标之和为常数,即c+d=10.再结合图像确定3 图3 评注:本题关键是以m为主元,把所求式子中的变量a,b,c均用m表示,由此将所求的多元代数式转化成一元,再利用函数的性质求解.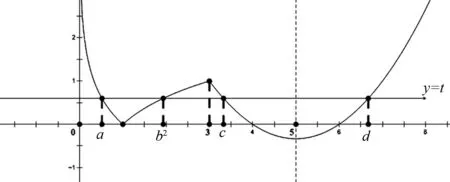
3.求等高线对应的交点横坐标函数的取值范围