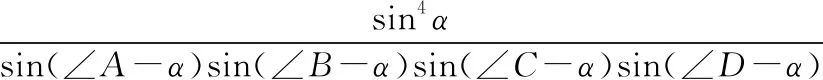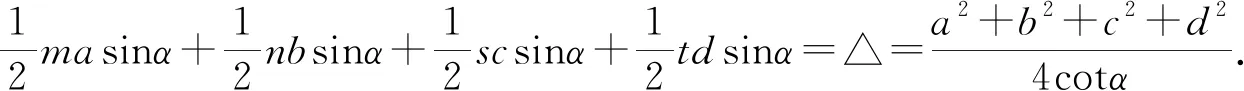四边形内勃罗卡角的三个公式

山东省滨州市沾化区第一实验小学 (256800) 曹景云山东省滨州学院理学院 (256600) 尹 枥

图1

若在四边形ABCD内，存在点P使得∠PAB=∠PBC=∠PCD=∠PDA=α,那么点P叫做四边形的勃罗卡点，而角α称为四边形的勃罗卡角.(见图1)

关于四边形内勃罗卡点的存在性问题在文[1]中有详细的讨论.本文假设所讨论四边形的勃罗卡点总是存在的.文献[2]中利用杨学枝的一个性质.给出了凸四边形内勃罗卡角的一个计算公式，之后文献[3]中利用正弦与余弦定理给出了四边形内勃罗卡角的几个计算公式.本文给出勃罗卡角的三个重要公式,进一步丰富了四边形内关于勃罗卡角的性质.为了叙述方便，假设四边形边AB,BC,CD,DA的长度为a,b,c,d，边AP,BP,CP,DP的长度分别为m,n,s,t，四边形ABCD的面积为△.

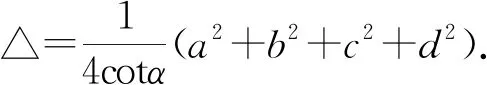
引理2[2]设a,b,c,d为四边形ABCD的四条边长，四边形ABCD的面积为△，则a2+b2+c2+d2≥4△.

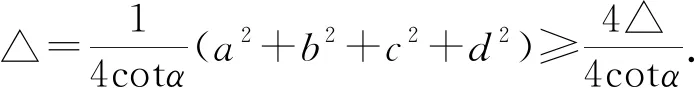
定理2 设角α为四边形ABCD的勃罗卡角，则sin4α=sin(∠A-α)sin(∠B-α)sin(∠C-α)·sin(∠D-α).

证明:在三角形ABP,BCP,CDP,DAP中利用正弦定理可得

将这八个等式相乘可得