圆锥曲线中线段之和的最值问题

广东省珠海第一中学 (519000) 杨 军

圆锥曲线中线段最值问题一般涉及解析几何的基本思想、基本方法.通过对直线、椭圆、双曲线、抛物线中线段的最值问题探讨，利用三角形两边之和大于第三边，两边之差小于第三边的原理，可以解决圆锥曲线这类线段之和最值问题，是研究性学习的体现，有益于培养学生的数形结合、转化化归等数学基本思想.本文列举数例予以说明.

1.求直线上的动点到两定距离最值问题

例1设点P为直线l:x+y-4=0上的动点,点A(-2,0),B(2,0),则|PA|+|PB|的最小值为.

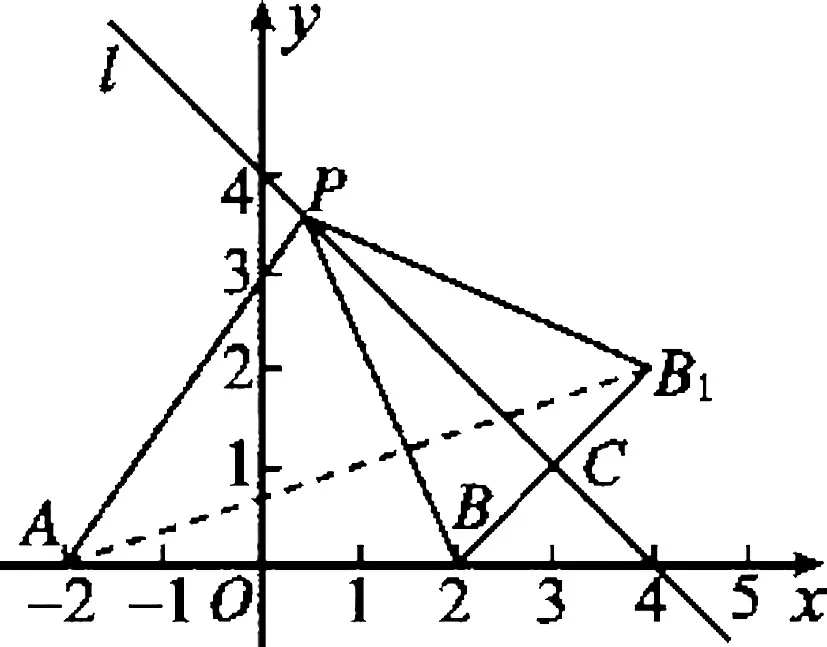
图1

变式例1条件不变，结论改为求|PA|-|PB|的最大值.

解：由三角形两边只差小于第三边知，当P,A,B三点不共线时，|PA|-|PB|<|AB|；当P,A,B三点共线时，|PA|-|PB|=|AB|.所以当P(4,0)时|PA|-|PB|有最大值|AB|=4.

评注：动点到两定点的距离之和最小时，两定点要在直线两侧；动点到两定点的距离之差最大时，两定点要在直线同侧.

2.求椭圆上的动点到两定距离最值问题

图2

图3

评注：求椭圆上动点到两定点的距离之和或之差时，先看定点在椭圆内部还是外部，利用三角形两边之和大于第三边或者两边只差小于第三边的结论，寻找共线时取到合适的最值.若不能直接找到最值，则可利用椭圆第一定义替换一个焦半径，而达到求解目标.

3.双曲线上的动点到两定距离最值问题

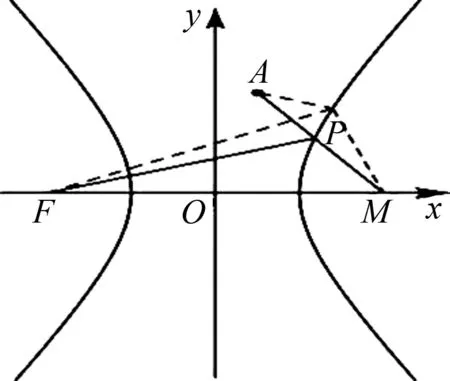
图4

解：如图4所示，对任意点P都有|PF|+|PA|>|AF|,此时不能直接找到最小值，可利用双曲线第一定义替换|PF|.设双曲线的右焦点为M，则M(4,0)，由双曲线的定义可得|PF|-|PM|=4，则|PF|=4+|PM|，所以|PF|+|PA|=|PM|+|PA|+4≥|AM|+4=9，当且仅当A,P,M三点共线时，等号成立.因此|PF|+|PA|的最小值为9.

评注：如果例3中A点是双曲线内部的一个点，则只要A,P,M三点共线时，就有|PF|+|PA|取到最小值.

4.抛物线上的动点到两定距离最值问题

例4设P是抛物线y2=4x上的一个动点，F是抛物线y2=4x的焦点，若B(3,2)，则|PB|+|PF|的最小值为.

图5

解：因为22<4×3，所以点B(3,2)在抛物线y2=4x的内部，如图5，过点B作BQ垂直准线于点Q，交抛物线于点P1，根据抛物线定义可得，|P1Q|=|P1F|，又P是抛物线y2=4x上的一个动点，所以|PB|+|PF|≥|P1B|+|P1Q|=|BQ|=4，当且仅当点P与点P1重合时，|PB|+|PF|取得最小值，且最小值为4.

评注：求解抛物线上一动点到定点(定点在抛物线内部)与焦点距离和的最值问题时，通常需要过该动点向准线作垂线，利用抛物线的定义，将问题转为求抛物线上一点到准线以及定点距离的最值问题，即可求解.

变式已知抛物线y2=4x上一点P到准线的距离为d1，到直线l：4x-3y+16=0为d2，则d1+d2的最小值为( ).

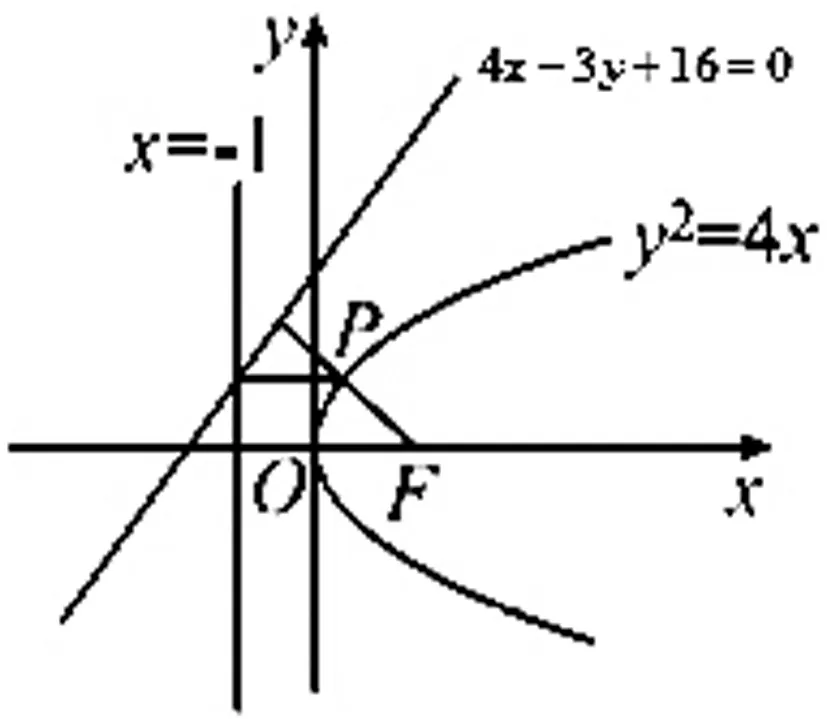
图6

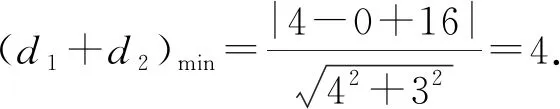
评注：利用抛物线的定义，可将d1+d2的取值转化为求点到直线的距离求得.