多基准轴透射式系统装调方法

杜国军，王春雨，欧宗耀，王 聪，胡 斌

（北京空间机电研究所， 北京 100194）

引言

某型号星载光谱仪聚焦于陆地生态系统植被和森林蓄积量探测，利用670 nm～780 nm 谱段的光谱获取空间连续分布的植被荧光信号，得到太阳诱导植被荧光遥感数据，从而准确绘制植被荧光时空分布规律，满足全球植被定量监测、森林植被生产力评估的需求。光谱仪采用光栅作为色散元件，由于分光系统的存在，系统会残余较大畸变，导致数据处理困难，星载光谱仪为了校正系统的畸变，成像透镜设计为离轴透射式光学系统，系统存在3 个光轴，光轴之间倾斜量达到0.606°，偏心量达到0.279 mm，增加了装调的难度。

光学系统的质量和光学元件的装调精度息息相关，国内外调研结果表明，透射式系统装调方法多为双光路定心法，定心仪测试透镜表面球心的跳动量给出球心位置，球心连线确定光轴，装调时最小化不同透镜光轴的偏心和倾斜，达到系统设计指标[1-6]。双光路定心法只适用于同轴透射式系统，对于离轴透射式系统的装调方法未见相关报道。光谱仪成像系统最大倾斜量超出了定心仪的装调范围，无法应用双光路定心法。针对这个难题提出了一种多基准轴的定心装调方法（MAA），通过结构预置偏心和倾斜的方法构建基准轴，利用光学平板实现光轴引出，将复杂的多光轴系统装调分解成单光轴系统装调，实现了离轴透射式光学系统的高精度装调。实测结果验证了该方法的有效性，为离轴透射式系统装调开拓了新的思路。

1 装调原理

1.1 成像透镜系统参数

光谱仪采用光栅和棱镜作为色散元件，成像组件采用离轴透射式系统，补偿由光栅和棱镜引起的畸变，可实现系统的畸变最小化。成像组件包含3 个光轴，光轴之间存在偏心和倾斜，如图1 所示。透镜1 和透镜2 组成光轴1，透镜3 和透镜4 组成光轴2，透镜5 为光轴3。光轴1 和光轴2 倾角为0.262°，偏心量为0.279 mm，光轴3 相对于光轴1 倾角为0.606°，参数如表1 所示。

图1 成像光学系统示意图Fig.1 Schematic diagram of imaging optical system

1.2 装调分析

畸变是实际像高和理想像高的偏差，根据δ初级像差理论，像差分为5 种初级像差，以5 个塞得和数表示。畸变是主光线的垂轴像差，表达式为

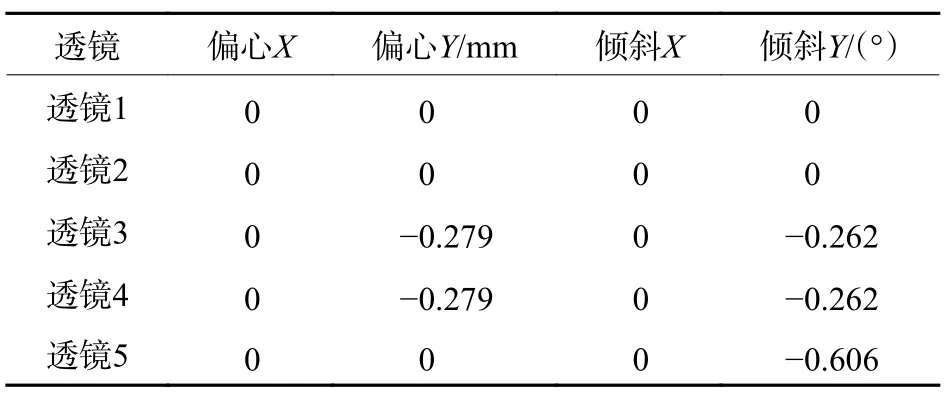
表1 透镜的偏心和倾斜参数Table 1 Parameters of lens eccentricity and tilt

根据塞得和数表达式：

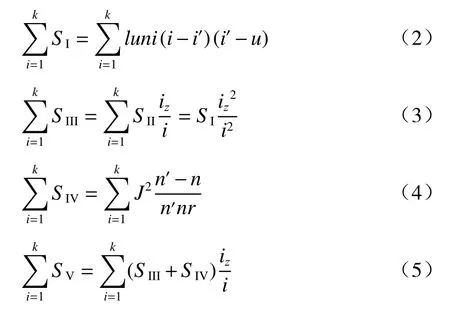
推导得出光学系统的畸变表达式：

简化后的畸变表达式为

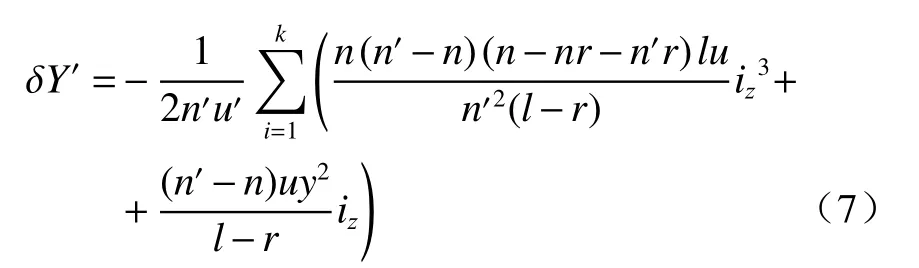
式中：n和n′为折射率；k为光学元件的数量；r为曲率半径；u为数值孔径；y为像高；iz为主光线和光轴的夹角。由公式（7）可知畸变与主光线和光轴的夹角以及像高正相关，本系统中数值孔径和像高无法改变，为了纠正畸变，透镜系统设计为离轴透射式系统，改变主光线和光轴的夹角。装调过程中精确控制离轴透镜组的倾角可有效控制畸变。

将实测的透镜曲率半径和中心厚度输入到光学系统优化设计软件中[7-8]，重新对系统镜间距和偏心进行优化，以光轴1 为基准，根据畸变计算光轴2 和光轴3 的失调量敏感度，如图2 所示。结果表明，当畸变小于3 μm 时，透镜偏心公差需小于0.05 mm，倾斜公差小于60″，镜间距公差小于0.05 mm，根据以往研究结果，直接装配无法满足系统要求[9-10]。

图2 畸变和失调量对应关系Fig.2 Relationship between distortion and misadjustment

1.3 MAA 装调方法

系统装调过程为最小化偏心以及倾斜量误差最小的过程，透镜组光轴偏差达到0.606°，超出了定心仪的测试范围，需要在系统中引入新的装调基准。考虑到装调公差相对宽松，提出了在透镜筒结构上一体化加工基准轴，预置光轴的倾斜量和偏差量，光学平板引出结构基准轴，应用OptiCentric双光路定心仪在新的基准轴上装调，将多光轴系统的装调分解成单光轴子系统装调，系统的装调流程如图3 所示。

图3 成像系统装调流程Fig.3 Assembly and adjustment process of imaging system

2 装调过程

2.1 机床定心

机床定心可去除光学件加工过程中产生的偏心和倾斜[11]，将透镜框的安装端面和透镜框的外圆加工成和光轴一致，如图4 所示。固定透镜组件到机床上，千分表测量透镜框外圈的圆跳动，调整使其和机床同轴，通过光学定心方法调整透镜的偏心和倾斜，使其光轴和机床转轴重合，加工透镜框的外圆和端面与透镜光轴重合。

图4 机床定心示意图Fig.4 Schematic diagram of machine tool centring

2.2 同轴系统装调

系统包含2 个同轴透镜组，单透镜机床定心完成后，选用OptiCentric 双光路定心仪进行定心装调[12]。调整透镜1 的光轴与定心仪的旋转轴一致，安装透镜2，通过垫片和侧面顶丝调整透镜2 的光轴与定心仪的旋转轴一致，如图5 和图6 所示。同理装调透镜3 和透镜4 组件。

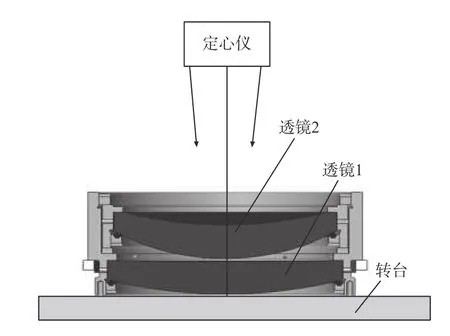
图5 同轴装调方法Fig.5 Coaxial assembly and adjustment method

2.3 光轴引出

系统包含3 个光轴，最大偏差0.606°，镜筒一体化加工预置偏心和倾斜，构建3 个基准轴，建立装调基准。如图7 所示，基准轴1 和镜筒外径同轴，基准轴2 相对于基准轴1 的夹角为0.262°，偏心量为0.279 mm，基准轴3 相对于基准轴1 的夹角为0.606°。

图6 同轴装调实物图Fig.6 Diagram of coaxial assembly and adjustment

图7 成像透镜框设计Fig.7 Design of imaging lens frame

基准轴的加工精度直接影响系统的装调精度，基准轴偏差计算公式为

式中： α为基准轴倾角；h1和h2为基准轴两侧的高度；D为基准内径。对公式（8）求导可得：

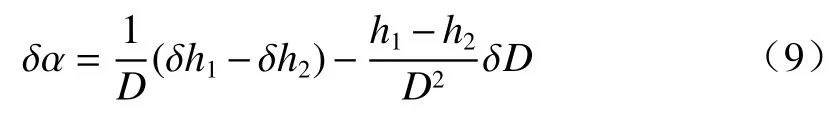
其中内径D为100 mm，对应0.606°的倾角，基准轴两侧的高度差为1.06 mm，公式（9）第2 项相对于第1 项可以忽略。提高基准轴精度的关键是控制h1和h2的加工精度，加工过程中重点保证基准面的高度差，加工完成后，高精度三坐标测量机测试表明，偏心公差优于0.02 mm，倾斜公差优于30″，能够 满足基准轴引出精度要求。

2.4 系统装调

装调过程如图8 和图9 所示。将镜筒固定在双光路定心仪的转台上，采用光学平板将光轴1 引出，结合杠杆千分表调整光轴和定心仪同轴，倾斜量小于10″，圆跳动量小于0.015 mm，作为光轴1 的基准轴。安装透镜1 和透镜2 组件，调整到倾斜偏差小于10″，偏心误差小于0.015 mm。将镜筒翻转180°，通过光学平板和杠杆千分表引出光轴2，作为透镜3 和透镜4 组件的安装基准。安装透镜3 和透镜4 组件时，调整倾斜偏差小于10″，偏心小于0.015 mm。光学平板引出光轴3，安装透镜5 组件，调整到倾斜偏差小于10″，偏心误差小于0.015 mm，完成系统偏心和倾斜的装调。

图8 成像镜头装调过程Fig.8 Assembly and adjustment process of imaging lens

图9 多基准轴装调过程Fig.9 Assembly and adjustment process of multi-reference axis

装调误差分布如图10 所示。从图10 可知，基准轴的引出误差为主要因素，通过进一步提高镜筒的加工精度可提高系统的装调精度。

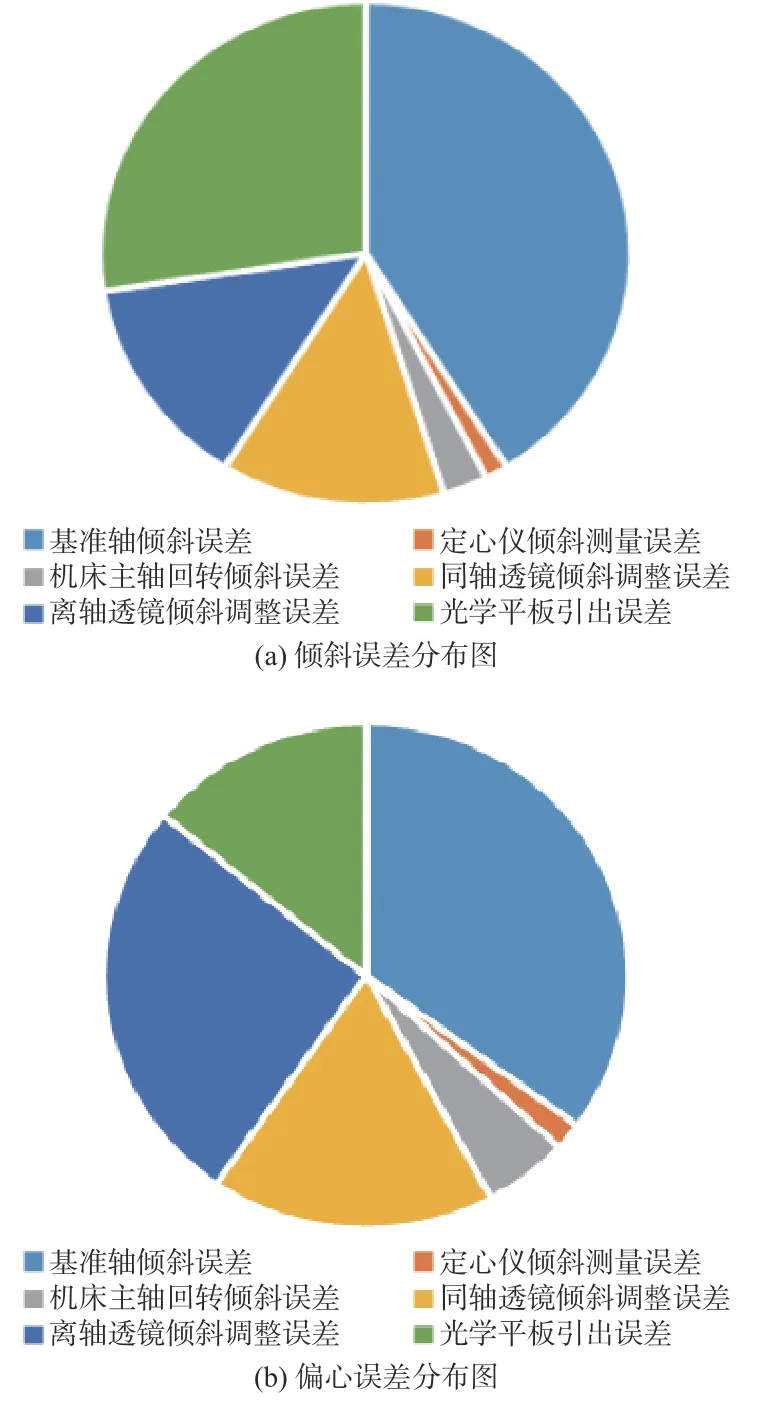
图10 偏心和倾斜误差分布图Fig.10 Distribution diagram of eccentricity and tilt errors

1） 镜筒同轴度误差。镜筒的同轴度为15 μm，千分尺的测量误差为1 μm，引起的镜头偏心误差为8 μm。

2） 镜筒基准轴偏心、倾斜误差。三坐标测量结果表明，镜筒偏心误差优于20 μm，倾斜误差优于30″。

3） 机床主轴回转误差。机床主轴引起的倾斜误差为2″，偏心误差为3 μm。

4） 定心仪测量误差。双光路定心仪倾斜测量误差为1″，偏心测量误差为1 μm。

5） 同轴透镜调整误差。透镜1 和透镜2 组件，透镜3 和透镜4 组件为同轴系统，调整误差较小，偏心可控制在10 μm，倾斜控制在10″。

6） 离轴透镜调整误差。透镜倾斜调整误差为10″，偏心调整误差为15 μm。

7） 光学平板接触误差。光学平板平面度优于10 nm，光学平板和结构面接触误差优于10 μm，镜筒的内径为100 mm，引起镜头倾斜偏差为20.6″。

综合以上误差，可计算得出透镜组的倾斜误差优于38.8″，偏心误差优于28.3 μm，满足系统的指标要求。

2.5 镜间距控制

同轴透射式系统的镜间距通过测试球面顶点得到[13]，球面顶点同时也是透镜的最高点或者最低点，对于离轴系统，透镜表面的最高点和最低点不再位于球面顶点，偏差量和倾斜偏心量相关，如图11所示。球面顶点A和表面最高点A′之间距离X如下式所示：

式中：a为透镜的倾角；R为球面曲率半径。

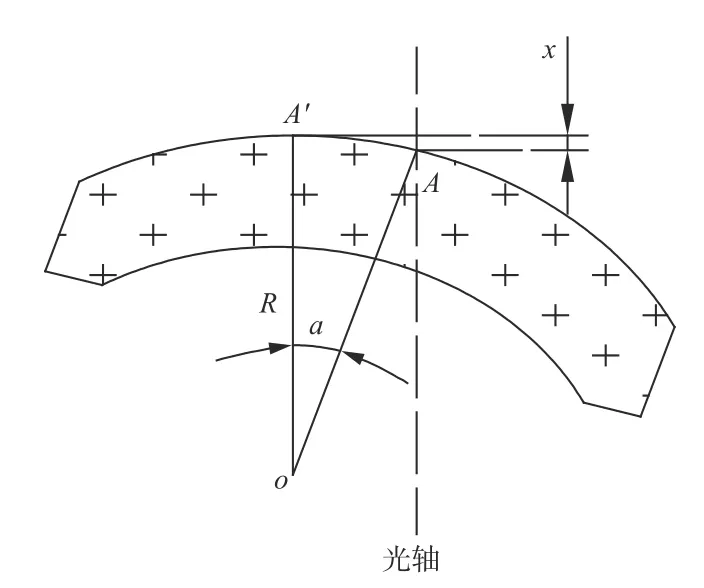
图11 镜间距测试原理Fig.11 Schematic diagram of lens distance test

根据公式（10）计算得出透镜最高点距离和透镜间距的差值如表2 所示。

表2 镜间距和测试距离对应表Table 2 Corresponding lens distance and test distance

在多基准轴装调过程中，通过接触式方法测量镜间距[14-15]，如图12 所示。首先测量透镜1 和透镜2 之间的镜间距以及透镜3 和透镜4 之间的镜间距，将透镜2 的光轴调整到和双光路定心仪的转台同轴，通过探针分别测量透镜1 和透镜2 上表面的顶点高度d1和d2。透镜1 和透镜2 的镜间距计算方法如下式：

图12 镜间距测试过程Fig.12 Test process of lens distance

式中：D2为透镜2 的中心厚度；D3为透镜3 的中心厚度。同理测量透镜3 和透镜4 镜间距D34。

透镜1 和透镜2 组件安装到镜筒中，测量透镜2 的上表面最高点H2，安装透镜3 和透镜4 组件，测量透镜4 上表面最高点H4，透镜2 和透镜3 的镜间距D23如下式：

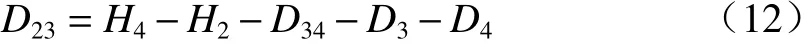
同理测量透镜4 和透镜5 镜间距D45。系统装调后实物图如图13 所示。

图13 成像镜头实物图Fig.13 Diagram of imaging lens

镜间距测量误差如表3 所示。探针2 次测量得出镜间距，系统装调倾斜误差优于38.8″，偏心误差优于28.3 μm，引起的镜间距测量误差≤1 μm，综合两种测量误差，镜间距测量误差≤14.2 μm，满足系统指标要求。

表3 镜间距测量误差Table 3 Measurement error of lens distance

3 装调结果

系统装调完成后，分别测试光轴1，光轴2 和光轴3，因为光轴1 和光轴3 的夹角为0.606°，超出了定心仪的测量范围，采用分段测试的方式，分别测试光轴1 和光轴2 的偏差，光轴2 和光轴3 的偏差，测试结果如表4 和表5 所示，与设计结果的偏差如表6 所示。最大偏心误差为25.4 μm，最大倾斜误差为17.7″，实际畸变和理论畸变对比如图14所示。从图14 可看出，最大畸变为2.77 μm，平均偏差0.32 μm，系统装调结果满足指标要求。

表4 透镜1 和透镜2 组件以及透镜3 和透镜4 组件的偏心倾斜Table 4 Eccentricity and tilt of lens 1, 2 and lens 3, 4

表5 透镜3 和透镜4 组件以及透镜5 组件的偏心倾斜Table 5 Eccentricity and tilt of lens 3, 4 and lens 5

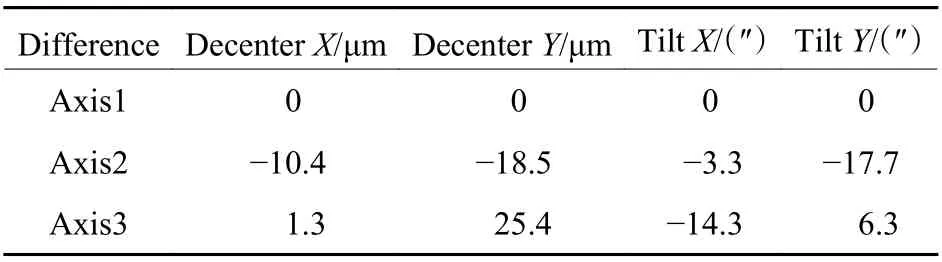
表6 透镜组的偏心倾斜偏差Table 6 Eccentricity and tilt deviation of lens

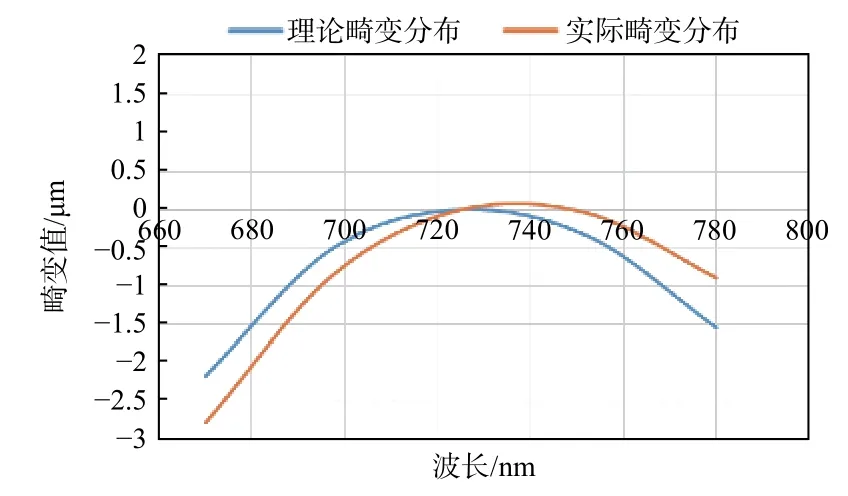
图14 理论畸变和实际畸变对比图Fig.14 Comparison of theoretical and actual distortion

4 结论

本文提出了一种新的离轴透射式系统的装调方法——多基准轴定心装调方法（MAA），克服传统的同轴透射系统定心装调缺陷，通过结构预置偏心和倾斜的方法构建基准轴，并辅助光学平板将复杂的多光轴系统装调分解成单光轴系统装调，利用此方法装调了光谱仪多光轴成像系统。装调结果表明，透镜偏心误差小于25.4 μm，倾斜误差小于17.7″，实现了系统的高精度装调。本装调方法不受定心仪测量范围的限制，可针对任意光轴的透射系统进行装调，突破了传统透射式装调方法的边界，为离轴透射式系统装调开拓了新的思路。