基于离轴数字全息改善散斑自相关重建效果

李 聪，徐 昭，陈 洁，倪 洋，周 昕

（四川大学 电子信息学院，四川 成都 610065）

引言

散射效应是由于传播介质的不均匀性引起光线向四周射去的现象。生活中的散射介质随处可见，比如：人体组织、磨砂玻璃、空气中的大雾或尘埃等。目前，在天文学、气象学、生物医学、光测量学等领域，经过散射介质对目标物体进行清晰成像的应用需求越来越广泛，但散射效应的存在却极大地限制了传统光学系统的成像性能。因为成像光束在经过散射介质透射或反射时，由于散射介质折射率的不均匀性，成像光束携带的目标信息在成像面会表现为明点和暗点随机分布的散斑。以往研究表明，虽然成像平面表现为一个随机的、不均匀的、没有任何目标信息的杂乱图像，但是散斑的大小、形状、位置和对比度既隐藏着成像目标的信息，又表现着散射介质的传输特性。

随着科学技术的快速发展，各种新技术被应用于解决散射介质成像的问题，已取得了许多的研究成果。例如：直接测量弹道光子的光学相干断层扫描技术[1]、鬼成像技术[2]、从天文学发展而来的自适应光学技术[3]、相位共轭技术[4]、反馈优化的波前整形技术[5]、基于光学传输矩阵的测量技术[6]、基于光学记忆效应（optical memory effect，OME）的散射介质成像技术[7]等。近年来，统计光学的兴起促进了散斑的相关成像技术[8]的进步。随着计算机技术的进一步发展，神经网络和深度学习方法作为解决散射介质成像的重要途径展现出巨大的潜力[9]。全息光学的应用也为解决散射介质成像的问题提供了新的技术方案[10]。1966 年Goodman等人提出利用波前重构方法提高通过散射介质时图像分辨率的全息技术[11]。1968 年Kogelnik 等人在Goodman 技术的基础上提出离轴全息技术[12]。同时，基于统计光学的全息图散斑相关2D/3D 成像技术也被提出，并用于散射成像领域[13-16]。

在已经提出的这些方案中，基于散斑自相关的成像方法主要是针对成像目标的几何尺寸位于散射介质的光学记忆效应范围内的情况，不过在应用该方法的过程中，由于成像环境噪声和仪器热噪声的存在，使得在利用单帧散斑自相关和相位恢复算法重建成像目标时，不能有效地抑制噪声来得到较好的重建效果。在本文中，针对成像目标位于散射介质的光学记忆效应范围内的情况，提出一种基于数字离轴全息减少重建图像过程中静态噪声影响的散斑自相关成像方法。首先利用离轴全息的衍射再现分离出成像物光束的散斑光场，然后利用相移法，差值运算相移前后的散斑光场，有效地消除成像物光散斑光场的噪声项，最后利用散斑自相关与相位恢复算法重建成像目标。

1 原理

当成像物体经过散射介质时，由于散射介质的存在，成像光束携带的目标信息在成像面会表现为明点和暗点“随机”分布的散斑，而且在实际成像的过程中，会存在不可避免的噪声，因此成像面上的单帧散斑强度可以表示为

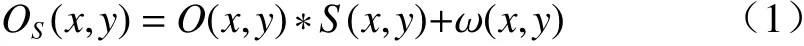
其中：O(x,y)表示未经散射的成像物面光场；OS(x,y)表示经过散射后的像面散斑光场；S(x,y)表示散射系统的点扩散函数； ω (x,y)表示在实际成像过程中存在的环境噪声和成像仪器的热效应造成的噪声项，主要为非时变的静态噪声项；*表示卷积运算。图1 是散射介质成像光路示意图。

图1 成像目标通过散射介质形成散斑Fig.1 Imaging target forms speckles through scattering medium

角范围可以大约写为θOME≪λ/πL[17]。将角记忆效应内成像系统的点扩散函数表示为S(x,y)，利用单帧散斑光场的自相关和相位恢复算法可以从散斑光场中重建成像目标[18]。当成像系统中存在噪声项时，根据自相关运算与卷积的性质，散斑光场的自相关运算可以表示为

讨论成像目标的几何尺寸位于散射介质的光学记忆效应范围内的情况，光学记忆效应是光在散射介质中传播时观察到的一种特殊现象，表现为在经过高度随机的散射介质时，如果成像光束的入射角度在一定范围内变化，此时在像平面上得到散斑图样的特征将保持不变，只是产生了一个整体的平移，成像物空间的各个位置具有空间平移不变的点扩散函数。散射介质的记忆效应的

其中： ⋆表示自相关运算； ∗表示卷积运算。由于在光学记忆效应成像范围内系统点扩散函数S(x,y)保持不变，因此点扩散函数之间的自相关S(x,y)⋆S(x,y)运算得到的是一个理想的二维脉冲响应函数δ(x,y)，上式计算中与ω(x,y)相关的噪声项最后使用C(x,y)替代，则（2）式表示为

由（3）式可知，散斑光场的自相关与物光光场的自相关函数之间存在着噪声项，如果在噪声项C(x,y)可以忽视，即当散斑信噪比非常高的理想情况下，可以根据维纳辛钦定理[9]从散斑光场OS(x,y)的自相关推导出物光场的功率谱密度，如（4）式所示：

其中F与F−1分别表示傅里叶变换与傅里叶逆变换，这表明在无噪声的情况下，散斑光场的自相关与物光场的功率谱密度成正比。由上式能够从散斑中获得成像目标的傅里叶域振幅信息。然而，通过计算散斑OS(x,y)的自相关不能得到成像目标的傅里叶相位信息，不能实现成像目标的重建。因此，需要进一步的通过相位恢复算法重建成像目标的傅里叶域相位信息。本文使用的是迭代GS 相位恢复算法，具体的流程如图2。

图2 GS 相位恢复算法流程图Fig.2 Flow chart of GS phase recovery algorithm

首先随机初始化入射光场的相位项，结合已知的物体傅里叶振幅项合成光场并计算二维光场的傅里叶变换，然后舍去傅里叶变换的幅值部分，保留其相位部分，同时将保留的相位部分与物光场的功率谱合成得到新的合成光场，计算新合成光场的傅里叶逆变换得到新的相位，如此迭代，光场最后趋于稳定。同时能从散斑中得到成像目标的傅里叶相位的信息，达到成像目标完全重建的目的。

但是利用（4）式单帧散斑重建的实际过程中，环境噪声和成像仪器的热效应噪声项C(x,y)通常不可忽略，噪声项的存在会对成像目标的重建效果产生较大的影响。因此本文将数字全息中的相移法用于去除实际成像过程中产生的噪声项，采用离轴全息结构作为实验的成像光路，设计离轴数字全息光路如图3 所示。

图3 离轴数字全息光路设计图。Fig.3 Optical path design of off-axis digital holography

图3 中，Laser 为激光器，C 为激光准直器，A1、A2 为小孔光阑，L1～L3 为正透镜，BS1～BS3 为光束分束器，M 为反射镜，P 为偏振片，SLM 为反射型空间光调制器，Object 为成像目标，D 为散射介质，CCD 表示散斑数字全息干涉图接收相机。如图3 所示，经准直器C、小孔光阑A1 和透镜L1 准直滤波后，激光经过分束器BS1 被分为两束光束，一束经过成像目标作为物光波，一束作为参考光波。当物光场经过散射介质D 时，成像光束携带的目标信息被扰乱为随机分布的散斑图样。参考光则经过分束器BS1 到达BS2 和偏振片P，当光束经过偏振片达到空间光调制器SLM 时，设置SLM 上每个单元的灰度值，可以给参考光场调制一个已知的相位分布函数φi(x,y)。参考光束与物光散斑光场最终经过合束器BS3 后干涉，经透镜L3 收集到CCD 平面上形成散斑数字全息干涉图样，产生的散斑数字全息干涉光场强度可以表示为

式中C1(x,y)表示在离轴干涉形成散斑的过程中存在的噪声项。为了有效消除噪声项C1(x,y)对物光重建的影响，我们使用任意一次相移法[19]，利用SLM 让参考光束引入一个已知的随机相位分布，然后用CCD 记录两幅不同相移情况下的全息干涉图样。即在已知原散斑干涉场（5）式中，利用SLM 给参考光引入一个随机的非 2π整数倍常数相移 φ，此时，散斑干涉场变为在的静态噪声项C1(x,y)消除差值得到：

将（5）式和（6）式所代表的两幅散斑干涉场进行差值运算，其中离轴干涉形成散斑的过程中存

随后在虚拟空间中进行波前重建运算，通过模拟原参考光场的菲涅耳逆向衍射进行重建。得到重建光场可以表示为第2 项表示重建物光散斑光场

2 数值模拟

2.1 仿真实验系统设计

设计了透射型物体散射成像的仿真实验，实验的成像光路如图3 所示，其中，激光器的波长为632.8 nm，CCD 面阵尺寸为4.5 mm×4.5 mm，分辨率为1024×1024 像素。物光和参考光形成的数字全息图的采样记录距离需要满足采样定理z0=(4D0L/λN)[20]，以使CCD 接收到较大的物光场能量及较高的频率角谱，其中D0表 示成像物体的宽度，L表示CCD 的面阵宽度， λ表示光波波长，N表示采样数。模拟透射型成像目标是数字“7”，如图4（a）所示，散射介质是用相位随机分布的广义孔径函数模型进行摸拟，得到的散斑图样如图4（b）所示。将散射介质置于成像物体后方50 cm 处，保证成像目标尺寸没有超出散射介质的光学记忆效应范围。选择CCD 的采样数N=1024，采样距离为1500 mm。空间光调制器SLM 给参考光场调制一个已知的相移项 φ =π/2。

图4 模拟透射性成像目标及其散斑图样Fig.4 Simulated transmission imaging target and its speckle pattern

2.2 仿真实验过程

为了实现离轴数字全息中重建物像与共轭像的完全分离，设定参考光场的方向余弦满足：(cosα,cosβ,cosγ)=(3L2/8z2,3L2/8z2,1)[20]，其中L2表示虚拟衍射重建平面的宽度，z2表示衍射重建距离，确保重建图像的中心坐标位于重建平面的(3L2/8,3L2/8)处。利用单次相移φ=π/2得到相移后的散斑干涉场，再利用差值运算得到（7）式中消除噪声项的干涉散斑图样如图5（a）所示。然后对所得到的去噪声干涉散斑光场5（a）进行衍射重建，得到图5（b）。截取分离的散斑物光场图5（b）中的方框部分如图5（c）所示。可以通过（4）式的自相关运算与相位恢复算法进行迭代计算，重建隐藏在散斑中成像目标，结果如图5（d）所示，其中图5（e）为重建的相位信息。作为对比，图5（f）和图5（g）分别为没有进行离轴全息去噪得到的物光散斑图样和利用单帧散斑自相关法重建得到的成像目标，图5（h）为相应重建的相位信息。仿真实验过程中使用高斯白噪声模拟实际成像过程中的噪声项。

图5 数值仿真实验结果图样Fig.5 Graphical results of numerical simulation experiments

2.3 实验结果与讨论

仿真实验结果表明，当成像目标的几何尺寸位于散射介质的记忆范围内时，利用物光散斑的自相关和相位恢复算法能对隐藏在散射介质后面的成像目标进行重建，如图5（d）和图5（g）所示。但是图5（g）没有进行去噪，重建出来的目标效果不是非常的清晰。这是因为在单帧散斑重建的成像过程中存在着噪声项，最终影响重建图像的效果。从图5（g）与图5（d）的对比可以看到，利用离轴全息的单次相移法能够有效地消除实验过程中静态噪声项对重建目标图样的影响，并且能够有效地重建更清晰的相位信息，如图5（e）与图5（h）所示。为了定量地说明重建目标的改善效果，引入结构相似度（SSIM）作为评价标准[21]，用来量化重建图像与成像目标的亮度、对比度和结构之间的平均结构相似性，取值范围为[0，1]，其值越高，表示重建图像的失真越小。

其中：ux和uy分别代表图像x,y的均值； σx和σy分别代表图像x,y的标准差；和分别代表图像x,y的方差； σxy表示图像x,y的协方差；C1和C2为常数。取C1=(K1×L)2，C2=(K2×L)2,为了避免分母非常接近数值0 造成的不稳定运算，取K1=0.01，K2=0.03，L=255[21]（像素值的动态取值范围）。不难得到图5（d）和图5（f）所对应的恢复成像目标的结构相似度分别为0.8796 和0.9875，从而定量说明了采用所提的离轴全息方法能够有效地抑制成像过程中的噪声项，提高了重建图像的质量。表1 给出了其他不同成像目标物体在使用所提出方法前后的重建模拟效果对比和相应的结构相似度。

从表1 的结果可以看出，采用离轴全息后重建目标的结构相似度（SSIM）都有所改善，说明所提方法对减少散斑自相关重建图像的噪声比较有效。

表1 采用离轴全息重建前后不同成像目标的重建效果对比和相应的结构相似度Table 1 Comparison of reconstruction effect of different imaging targets before and after off-axis holographic reconstruction and corresponding structural similarity

3 结论

在本文中，我们提出一种基于数字离轴全息技术改善散斑自相关重建图像效果的方法。针对成像物体的几何尺寸在散射介质的光学记忆效应范围的情况，利用离轴全息技术获得目标物体经散射介质后的全息干涉图，再采用相移法通过空间光调制器使参考光束引入任意相位分布，得到另一幅全息干涉图，并将两幅全息干涉图进行差值运算以消除环境噪声和热噪声的干扰，然后通过衍射的逆运算直接重建无干扰的物面散斑光场，最后通过散斑自相关与相位恢复算法有效重建成像目标。通过仿真实验对比使用离轴全息方法前后的重建效果，并采用结构相似度参数对重建效果进行了定量分析，证实了所提方法能够有效改善重建目标的质量。这种方法的成像步骤简单，只需要记录两幅散斑图样就能快速恢复成像目标的信息，实现快速成像，而且该技术采用的是离轴数字全息，在通过散射层对目标进行三维成像方面也具有应用潜力。