考虑修复非新的多组件DTS设备的状态维护建模

葛亚雄，周晓军

(上海交通大学工业工程与管理系，上海 200240)

0 引言

随着生产设备的组件数目日益增多，其集成化与智能化程度不断提升，状态维护(Condition-based Maintenance，CBM)逐步得到推广应用，与此同时，设备对外部条件的变化也越来越敏感，企业的维护管理面临重要挑战。

设备的日常工作负荷会使组件内部性能逐渐衰退，企业通过实施CBM，对设备内部状态进行实时监测，有针对性地预知故障信息，并安排检修计划。而与此同时，由于人员、工况、环境等不确定性外部因素的冲击，设备时常产生突发性的随机故障，导致难以预测的成本损失。对于同时面临内部衰退和外部冲击的设备状态维护问题，许多研究运用DTS(degradation-threshold-shock)模型描述其故障规律[1-8]。Lemoine等[1]将DTS模型中的设备故障定义为磨损超过可接受水平或发生致命冲击;Caballé等[2]考虑了衰退的产生与生长，并建立了考虑多衰退点的DTS模型;Yang等[3]研究了具备正常、缺陷和故障3种运行状态的DTS系统模型。该类DTS模型大多基于修复全新的假定，对于一般DTS生产设备，由于组件特性、人员技能熟练度等因素，日常的维护保养不一定能使组件回复到全新状态，修复非新是普遍情况。许多学者也对CBM 中的修复非新进行了建模研究[9-11]，其针对单组件系统分别采用截尾正态分布和均匀分布模拟修复非新效果，且均假定修复后状态回复的期望值为当前状态的50%，而多组件DTS型生产设备的不同组件的可修复性一般不同，如机床主轴只能被一定程度地修复，而车刀可修复至接近全新，显然该类模型难以描述多组件的DTS系统的差异性修复非新。此外，为了制定面向DTS生产设备的CBM 维护策略，通常需要考虑生产设备的多组件特性，并充分利用组件的状态信息。现有研究常用“阈值-周期”策略[12-15]，即实施固定周期的状态检测，当状态超过阈值时即进行维护。这类模型多针对单组件设备，对于多组件DTS生产，组件数增多导致“周期”、“阈值”变量的急剧增加，进而使得策略难以实现求解，同时，固定的检测周期也使得决策者未能充分考虑状态信息，以灵活地决定检测时机，更为合理的方式是根据设备的状态信息，动态调整设备状态检测的时间间隔。

因此，为了有效建立面向多组件DTS设备考虑修复非新的状态维护模型，本文利用对数正态分布模拟不同组件的修复性差异，构建面向多组件的修复非新模型，在此基础上，建立了基于“综合状态阈值-变周期检测”的状态维护策略和决策模型。一方面，引入设备的综合状态参数，减少状态维护模型中的“阈值”型决策变量;另一方面，引入状态协变量函数，构建了基于设备状态信息的可变检测周期模型。

1 系统故障与修复性建模

1.1 系统模型假设

考虑一台有n(n≥2)个关键组件受监控的DTS设备，设备各组件同时面临内部衰退和外部冲击。设备满足以下假设:

(1)受监控组件i(i=1，2，…，n)的衰退过程表示为状态量的连续增长的随机过程{Xi，t，t≥0}，初始状态Xi，0=0，所有组件之间的状态衰退过程相互独立。

(2)当组件状态量超过某一阈值L时，组件产生衰退失效。任一组件的失效都会导致设备停机，并产生停机成本。

(3)为避免衰退失效的产生，对组件进行预防维护，预防维护具有修复非新特性，所有组件都是可修复的。

(4)状态检测非连续并按周期进行。检测并得到组件实时状态、执行组件的预防维护、发现并修复组件的衰退失效只有在状态检测时才会发生，且三者的完成时间很短，可忽略不计。

(5)受监控组件的状态衰退会使设备更易发生冲击故障，冲击故障会被即时发现并修复，同时造成大量修复成本。组件的状态衰退过程不受冲击影响。

1.2 故障建模

1.2.1 组件的状态衰退建模

设备的日常工作负荷会导致组件随时间增长而出现疲劳、磨损或裂纹增长等状态衰退过程，在状态监测下，这些衰退过程通常表现为状态量的单调增长过程，而Gamma过程可有效表征机械设备状态衰退的独立增量特性[16-17]。假设Xt为组件在任意时刻t的状态量，经过一段时间τ后，组件状态的随机增量Xt+τ-Xt服从Gamma分布，其概率密度函数为:

式中α和β为Gamma分布的尺度和形状参数，组件单位时间的衰退增量期望为:

基于式(2)结果，设v=αβ，称v表示组件的衰退速度。

1.2.2 设备随机冲击故障建模

除了内在的状态衰退，设备在工作过程中也面临着如频繁启停、断电和人员操作失误等外部因素的冲击，此类随机冲击的故障规律可使用泊松点过程有效模拟。设Nsho，t为[0，t]时间区间内发生的冲击故障的累计次数，基于泊松过程，在任意长度为τ的时间区间内，设备发生冲击故障的次数ΔNsho，τ=Nsho，t+τ-Nsho，t服从参数为λτ的泊松分布，其概率函数为:

式中λ为泊松过程的强度，即单位时间内发生冲击故障次数的期望，即E[ΔNsho，1]=λ。当λ为一个常数时，称该泊松过程是齐次的。

制造业生产中，随着设备使用年龄的增长，其关键组件逐渐老化，设备面临冲击时发生故障的可能性也随之增加。为了描述这种实际现象，在现有研究中，Shafiee等[6]和Huynhabaac等[18]分别引入了设备役龄-泊松过程强度函数，以实现冲击故障的逐步增加;而Caballé等[2]和Kahle等[19]则假设设备衰退超过某一程度泊松强度则会发生突变，进而增加冲击故障的风险。前者基于役龄的强度定义方式使其无法应用于基于状态量的维护建模中，而后者突变型的描述方式则并不符合一般设备的连续衰退特征与故障规律。为了量化描述设备状态对设备冲击故障率的影响，本文基于比例故障率模型(Proportional Hazard Model，PHM)[20-21]的建模思路，通过引入整合组件状态的非齐次泊松过程(nonhomogeneous poisson process)来描述设备的随机冲击故障规律，其强度函数可表示为:

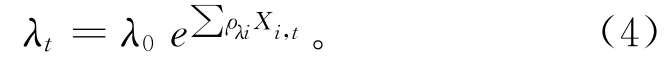
式中:λ0为设备在基准状态下，即组件状态Xi，t=0(i=1，2，…n)时的泊松过程强度;e∑ρλi Xi，t为状态协变量函数;ρλi＞0为组件i的相应参数。此时，经过单位时间设备发生冲击故障次数的期望为:

式中:t为任意时刻，u为积分变量。

1.3 基于状态的修复非新建模

制造业设备组件的维护中，通常需要考虑修复非新，一方面，维护后的组件通常难以恢复全新，会有一定的衰退剩余(组件物理特性衰退只能被有限程度地修复)，不确定性因素也决定了维护效果具有随机性(如维护人员技能不熟练、工具损坏);另一方面维护也会导致组件衰退速度加快(维护可能损害组件的装配特性和其他物理特性)，且一般状态修复效果越差这种不利影响越大。因此，修复非新建模分为衰退剩余和衰退加速两方面。

1.3.1 衰退剩余建模

对多组件设备的修复非新特性进行建模时，不仅要考虑衰退剩余的随机性，还要考虑不同组件修复特性的不同。现有文献多采用截尾正态分布、均匀分布等描述状态回复效果[9-11]。这些模型多针对单组件系统，且维护行为具有相同的期望效果，无法有效表征设备各组件的不同修复特性。此外，由于人员的操作失误等因素，维护行为也有可能使组件的状态变差，而现有研究并未考虑这一情况。为此，假设预防维护后的组件有一个随机的衰退剩余量，其服从对数正态分布(lognormal distribution)[23]。设预防维护前组件i的状态为，预防维护后的衰退剩余服从参数为(μ，σ)对数正态分布，其概率密度函数为:

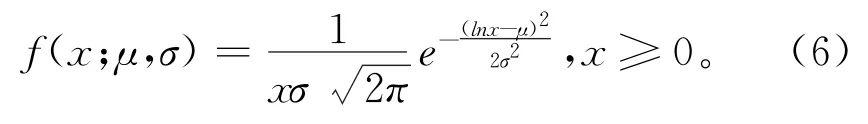
式中:μ=ln(δi)，δi∈(0，1)为组件i的修复特性参数，其大小代表了组件的期望可修复性。基于此分布可知衰退剩余量的期望值为:

为了简化参数的求解过程，同时保持对数正态分布的基本分布特性，可取σ为一较小的固定值(0＜σ≤0.1)，则衰退剩余量的期望值为:

1.3.2 衰退加速建模

维护会导致组件衰退加速，设组件i维护前后的衰退速度分别为，则衰退加速Δvi=为一非负的随机变量，可建模为服从指数分布[9]，其概率密度函数为:

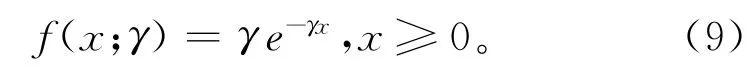
式中，γ为分布参数，代表指数分布的数学期望值。考虑到预防维护的衰退加速与维护效果的相关性，对组件i，将分布参数γi定义为:

式中γ0为一调整参数，以比例形式代表实际的状态回复效果，这样，当状态回复效果较好时，较大，造成的期望衰退加速也较小。其效果图如图1所示。

2 状态维护建模

2.1 维护策略

传统的状态维护策略通常采用“阈值-周期”策略，即为每个组件设定状态阈值，并按照固定周期监测其当前状态，随着组件的增加，该策略极易导致维护决策变量即阈值数量的快速增长，进而加大模型求解的难度，且固定的监测周期也不适应动态的组件状态环境。为此，本文针对设备的多组件特性，建立一种面向多组件环境的“综合状态阈值-变周期检测”的状态维护策略。在该策略下，对于具有n个组件的DTS系统，其维护决策流程可表述为:

步骤1设备运行参数初始化并开始运行，同时给定初始的综合状态阈值M，基础周期参数T。

步骤2进行状态检测，根据各组件的状态Xi，t得到系统的综合状态Xc，t。当Xc，t≤M时，所有组件不进行维护;当Xc，t≥M时，对任意组件i，若Xi，t＞Li则对其进行替换维修，否则对其进行预防维护。

步骤3根据基础周期参数T和当前的各组件状态计算下一个状态检测时间点tj，并使t=tj。若t超出规划期时间域[0，H]则执行步骤4，否则转步骤2。

步骤4统计规划期内的冲击故障发生次数Nsho，H并计算维护总成本，找出总成本最小时对应的(M，T)取值，即为最优维护策略。

为实现上述维护决策过程，首先需对设备的综合状态阈值，以及基于基础周期参数和组件状态的设备可变检测周期进行建模，其次构成本型目标函数建。

2.2 综合状态阈值

综合状态阈值是由各受监测组件的实时状态计算得到的设备整体状态指标，定义为:

式中θi为组件状态的权重系数，表示组件在维持设备工作状态中的相对关键程度。组件的重要性评价常见于多组件系统的维护研究[22]，其评价和取值标准可根据实际的应用场景确定，在本研究中，假定组件的重要性与其维护成本呈正比。

在该定义下，状态检测时可得到设备的实时综合状态Xc，t，并根据Xc，t是否超过综合状态阈值M作出具体维护决策。

2.3 可变检测周期

现有状态维护策略的状态检测一般取固定检测周期，缺少对设备实时状态信息的考量。为此，引入状态协变量函数建立可变检测周期模型，设备的第j+1个检测时间点tj+1由上一检测时间点tj和基础周期参数T共同决定，定义为:

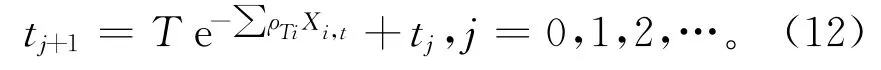
式中ρTi＞0为组件i的状态量的权重参数。基于该定义，设备的下一次检测时刻需根据本周期末的设备状态动态调整，且下一个检测周期长度与本周期末的状态协变量呈反比关系。当本检测周期末的设备状态较好即取得较小值时，设备状态处于预防性维护阈值M以下的预期时间较长，则下一个检测周期相对较长;反之，当本检测周期末设备状态较差时，下一个检测周期则相对较短。权重ρTi的取值可根据实际情况适当选取，数值越大则相应组件状态的影响程度越高。此外，根据式(13)，检测周期Tj的实际取值范围满足:

2.4 目标函数构建

DTS设备在规划期内产生的维护总成本主要包括总状态检测成本、总预防维护成本、总替换维修成本、总衰退停机成本和总冲击故障成本，根据系统故障模型和维护策略，对于一个组件数为n的系统，在规划期[0，H]内的维护总成本可表示为:

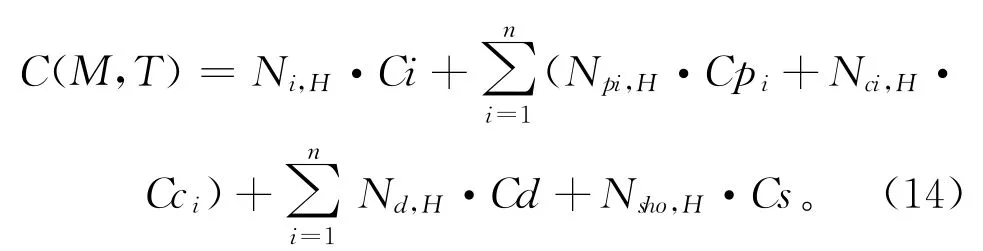
式中:Ni，H、Nd，H、Nsho，H、Npi，H和Nci，H分别为为规划期[0，H]内的状态检测、衰退停机、冲击故障、组件i的预防性维护和组件i的替换性维修的次数;Ci、Cd和Cs为状态检测、衰退停机和冲击故障的单次成本;Cpi和Cci为组件i预防维护和替换维修的单次成本。假定单次成本的大小关系为Cs＞Cc＞Cp＞Cd＞Ci。

式(14)中，状态维护的决策目标是对于不同的决策变量(M，T)，找到使规划期维护总成本最小的变量组合(M*，T*)，即

3 算例分析

由于组件状态衰退过程、外部冲击过程以及非新修复中存在大量的随机因素，导致规划期内的成本C(M，T)几乎无法解析求解，因此基于MATLAB平台，采用蒙特卡罗(Monte Carlo)仿真方法对模型进行决策优化。蒙特卡罗仿真的流程如图2所示，在仿真过程中，将规划期[0，H]内的时间离散化，每运行一个时间单元τ，即根据相应分布生成随机数，从而得到组件衰退增量、冲击故障次数以及可能的状态回复效果和衰退加速效果;在运行到状态检测时间点后，根据维护策略实施维护动作，进而确定下一次检测的时间;整个规划期运行完后，就可得到本次仿真的总成本;此外，为了减小各种随机分布导致的不确定性，对每次仿真都进行了足够多次的重复，取结果的统计平均值作为最终估计值。为了优化得到最佳的维护决策，采用网格搜索算法，通过对不同组合的综合状态阈值M和基础周期参数T进行仿真，根据总成本最小原则，即可得到两个参数的最优组合（M*，T*）以及最小规划期总成本C*。

针对一个组件数n=2的系统，假定组件的衰退故障阈值L1=L2=100，其他模型初始参数如表1所示。

表1 模拟仿真初始参数

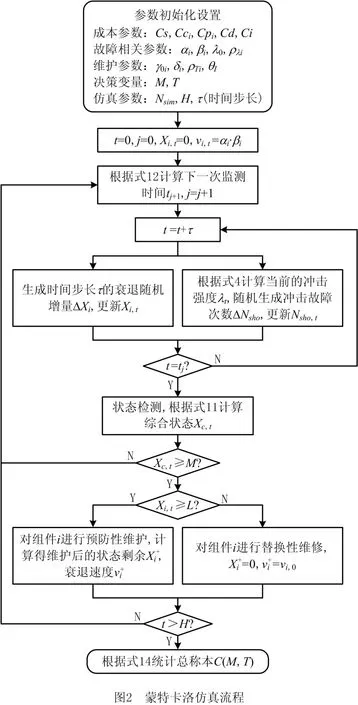
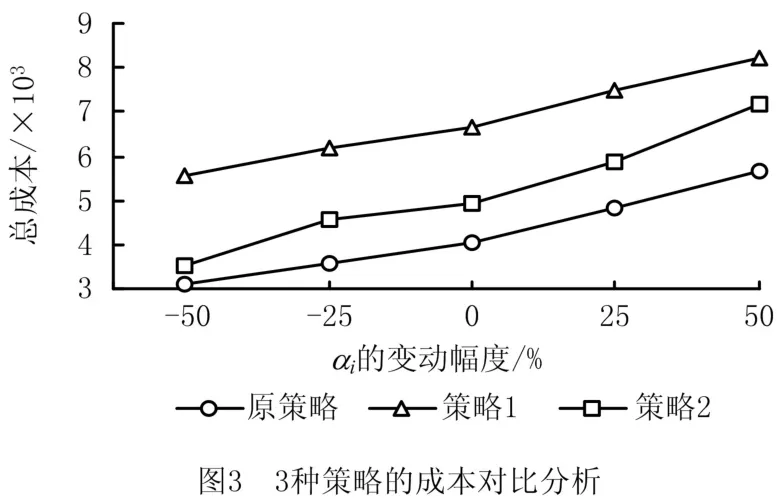
表1中:αi、βi、γ0i、δi分别为组件i(i=1，2)的衰退过程尺度参数、衰退过程形状参数、衰退加速调整参数、修复效果参数;λ0为设备在基准状态下的泊松过程强度;ρTi、ρλi分别为可变周期模型、非齐次泊松过程模型参数;Nsim为单次仿真的重复次数。在上述参数设置下，得到的结果为M*，T*=46，9，相应的维护成本为c*=40 432。为检验所提出维护策略的合理性，进行了策略对比分析，对照策略分别为策略1(多个组件视为独立系统，单独采用本文策略)策略2(维护策略中只考虑替换维修，未发生故障的组件不维护)。在不同衰退速度系统下对3种策略进行了对比分析，结果如图3所示。

由图3可以看出，对于不同衰退速度的系统，原策略都取得了最佳的结果，这表明修复非新的引入有利于节省维护成本。

为了进一步验证模型的合理性，了解模型参数对实际维护策略及成本的影响，算例分析分为组件特性参数分析、成本参数分析和策略可行性分析3部分。

(1)组件特性参数分析

组件的特性参数主要包括衰退速度和修复特性两类。针对状态衰退速度，以表1中的参数为对照，以相同倍率整体调整α1，α2，保持β1，β2不变;针对修复特性，除了对δ1，δ2进行整体调整外，还研究了δi(i=1，2)单独变化时维护策略与成本的变化规律。仿真结果如图4，以及表2和表3所示。

分析图4结果可知，当组件的衰退速度整体增加，基础检测周期T*逐渐减小，规划期内的状态检测次数随之增加，以避免可能出现的衰退失效及其相应成本。同时，状态检测次数的增加意味着规划期内潜在的预防维护次数增多，预期的预防维护成本增加，为了对其进行控制，则需要适当提高综合状态阈值M*，以降低在相同的组件衰退速度下设备综合状态Xc，t超过阈值M的可能性，从而抵消预防维护次数增多的趋势。

由表2可知，随着组件的修复特性整体变好(修复特性参数减小)，M*逐渐减小，导致在相同衰退速度下，状态检测时综合状态Xc，t超过阈值M*的可能性增加，进而使规划期内的预防维护次数增多，降低了总的替换维修成本和冲击故障成本，进而降低了总成本。同时应注意到，修复特性的提升与成本的降低并不是线性关系，修复性越高，提升修复性获得的成本变化越小，实际中，考虑到提升组件修复性的本身成本，其甚至可能不利于总成本的减少。此外，当某一组件的维护回复效果δ＞0.5时会出现大量无效修复，即预防维护使组件的状态变得更差，由于实际场景中无效修复为小概率事件，表2未给出优化结果。

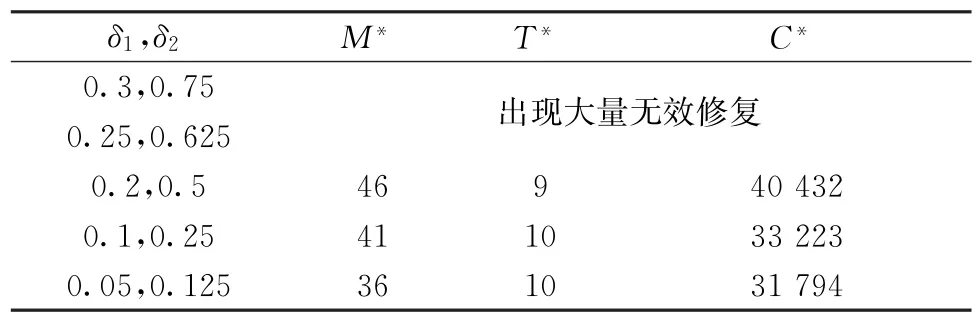
表2 组件修复特性整体变动分析

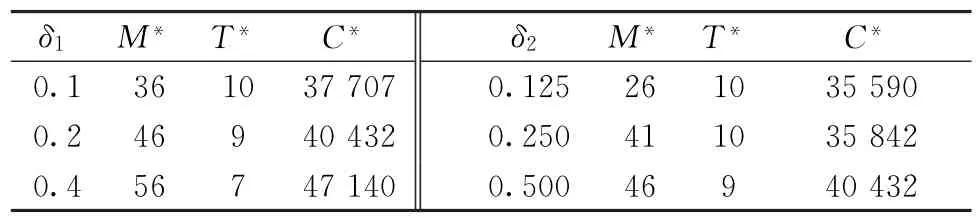
表3 组件修复特性单独变动分析

表3分别研究了组件1、组件2的修复特性参数δ1、δ2单独变化对维护策略及成本的影响。分析可知，组件修复特性单独变化和整体变化对仿真结果的影响基本一致，重要度更高的组件(本例中为组件1)的修复特性变化对成本的影响更大，符合实际情况。

(2)成本参数分析

下面对状态检测成本Ci、冲击故障成本Cs、替换维修成本Cc和预防维护成本Cp四种成本进行参数分析。其中替换维修成本Cc和预防维护成本Cp的参数分析中，分别对Cc1，Cc2和Cp1，Cp2按相同倍率进行整体调整。仿真结果如表4所示。

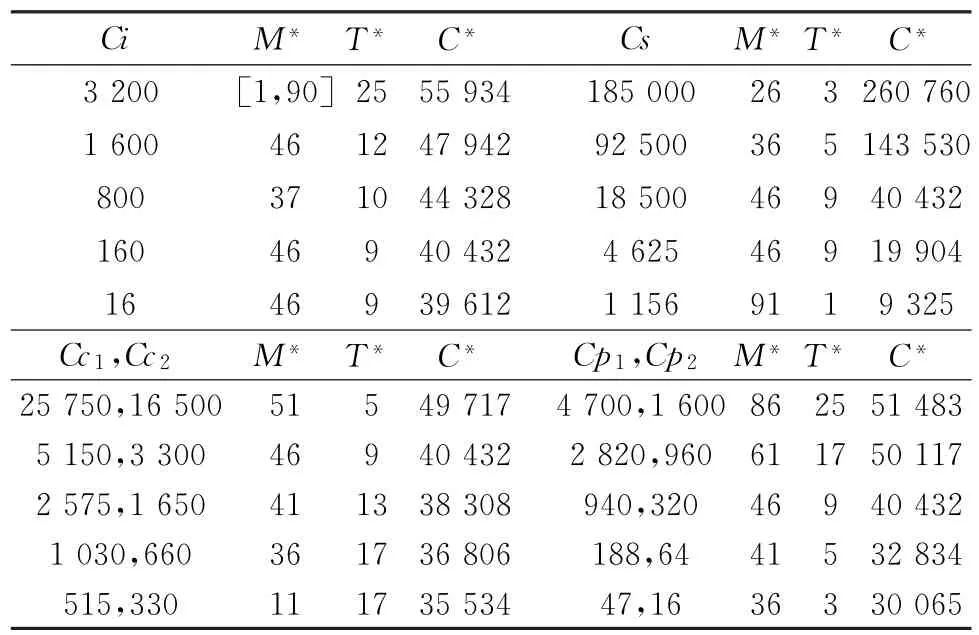
表4 成本参数变动分析

分析表4中状态检测成本Ci变动时的仿真结果可知，Ci与T*为负相关关系，这表明单次检测成本增加时，应延长检测周期，从而减少规划期内的检测次数，以降低规划期内的总检测成本，符合预防维护的实际需求。

由表4中冲击故障成本Cs的变动分析可知，当Cs在一定范围内(4 625～185 000)逐渐上升，即整个规划期内冲击故障造成的损失变大时，应制定更积极的维护策略，低阈值频繁检测，以使设备的组件状态维持在较低水平，进而降低冲击故障发生次数;而当Cs=1 156，设备的冲击故障成本与预防维护成本(Cp1+Cp2=1 260)大致相当，此时应该频繁检测，提高综合状态阈值M*以慎重作出维护决定，因为此时预防维护成本Cp与替换维修成本Cc远高于其他成本，提高阈值M*可以减少规划期内的预防维护次数，而频繁进行状态检测则可以最大程度避免组件衰退失效，进而有效控制规划期内的总预防维护成本与总替换维修成本。

由表4中Cc1，Cc2和Cp1，Cp2变动时的仿真结果可知，预防维护成本Cp和替换维修成本Cc的变化对检测周期的影响是相反的，这反映出实际中预防维护对替换维修(衰退失效)的制约效果。进行预防维护可减少组件的衰退失效进而避免替换维修成本，由于预防维护总是在状态检测时进行，规划期内的状态检测次数决定了预防维护次数，因此当单次预防维护成本Cp上升，则应延长检测周期，以减少预防维护次数及总的预防维护成本;而当单次替换维修成本Cc上升，则应缩减检测周期，以增加预防维护次数，使组件保持较好状态，进而减少总的替换维修成本。另一方面，Cp和Cc的变化对综合状态阈值M*的影响趋势是一致的，这是由DTS模型中冲击故障的存在导致的。当预防维护成本Cp减小，由于泊松冲击过程强度由组件的状态决定，应降低T*增加预防维护次数，同时降低阈值使组件保持较好状态水平，以减少冲击故障的发生;而当替换维修成本Cc减小，冲击故障成本在所有成本中的比重增加，这时同样应降低维护阈值，保持较好的组件状态，以尽可能减少冲击故障。

(3)维护策略的可行性分析

事实上，本文所提出的维护策略在理论上也存在一定缺陷，其无法有效兼顾多组件DTS设备在实际应用场景中可能会遇到的两种维护需求。①在第j次状态检测时，若得到综合状态≤M，按照既定策略所有组件均不需预防维护，但如果此时存在个别组件失效，即∃i∈{1，2}使＞Li，设备会因为组件衰退失效而停机，显然，该情况下设备不实施维护是有悖常理的;②在第j次状态检测前的某一时刻t，设备可能已经因组件衰退失效而停机，即在t时，∃i∈{1，2}使＞Li，其中tj-1＜t＜tj，在此情况下，状态检测滞后于设备实际故障的发生，若不提前进行状态检测，当滞后时间过长则可能造成大量成本损失。

为此，本文对两种维护需求出现的可能性进行了分析。对于第①种情况，采用其在规划期[0，60]内的发生次数Nf代表其发生可能性;对于第②种情况，则统计了规划期内所有状态检测的滞后时间的平均值Tlag，以检验发生长时间检测滞后的可能性。如图5所示为不同衰退速度的系统在采用最优维护策略时(如表2)两种需求的发生情况，其中的数据为1 000次蒙特卡罗仿真的平均结果。

由图5可知，对于多组件DTS系统，采用本文所提出的维护策略时，第①种需求情况几乎不会发生，且第②种情况的滞后时间相对较少，且系统衰退的越快，滞后时间越少，这表明本文的维护策略具备较好的实际可行性，且对高衰退速度的系统的可行性更为突出。

4 结束语

本文以实施状态维护的多组件DTS设备为研究对象，构建了设备内外交互型衰退模型和多组件的差异性修复非新模型，进而通过引入综合状态参数，建立了“综合状态阈值-变周期检测”的维护模型。仿真结果验证了模型的有效性，同时表明维护策略相较组件单独维护和不考虑修复非新的两种策略具有成本优势。通过参数分析可看出，不同条件下通过平衡修复非新、组件替换和冲击故障3种成本即可得到最佳的维护策略，降低冲击后果在一定程度内最有利于成本节约。另外，本文的综合状态模型中假定权重系数正比于组件的维护成本，事实上，结构关系等因素也常被用于评估组件关键程度，下一步将对此进行深入研究。