自适应Fourier分解思想在再生核W2 1 [a,b]空间的应用
2021-04-12蒋文超谭立辉
蒋文超,谭立辉
(广东工业大学 应用数学学院,广东 广州 510520)
在信号处理领域,为了实现信号的分类、存储、识别等目的,通常需要将信号分解为不同的原子,研究它们的不同表示形式。而稀疏表示的目的就是用尽可能少的原子来表示信号,以获得信号更为简洁的表示形式和更容易地获取信号所蕴含的信息,实现信号的压缩、存贮等目标[1-3]。经典的信号分解模型有Fourier分解、短时Fourier分解、小波分解等[4-5]。在1998年,N.E.Huang等人提出了经验模式分解算法(Empirical Mode Decomposition,简称EMD),它能将任意复杂信号 f(t)分解为数目有限的本征模态函数之和
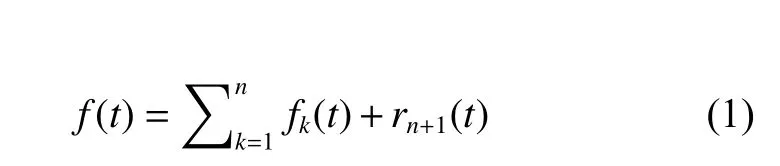
其中 fk(t)为本征模态函数(Intrinsic Mode Functions,简称IMF)[6],rn+1(t)为余量。借助于D.Gabor在1947年提出的用解析信号的方法来定义IMF的瞬时频率的结论[7],通过对每一个IMF的 fk(t)做Hilbert变换H,可得到其对应的解析信号为




关于这个算法极大值选取的存在性及算法的收敛性证明具体参见文献[22]。围绕这个分解,钱涛教授及合作者[23-26]开展了一系列的工作,他们不仅从理论上证明了AFD算法的快速收敛性,而且实现了在系统辨识、图像去噪等领域的应用,并将AFD分解的相关结论推广到矩阵值函数、高维复分析、Clifford分析等领域。
由于自适应Fourier分解是基于Hardy空间的性质建立的分解模型,而Hardy空间本质上是一个再生核空间。为了拓宽其应用范围,本文将研究再生核空间W21[a,b][27-29]的自适应Fourier分解算法,利用能量下降最快的原理自适应性地构造出最佳n 项逼近函数,从理论上证明其收敛性及极大选择原理成立。最后用实验验证在 W21[a,b]再生核空间中利用自适应Fourier分解原理构造的n 项最佳数值原函数的逼近效果要优于用等分节点构造的 n项最佳数值原函数。并且随着节点数的增加,两个方法的逼近误差都会逐步变小。
1 W21空间的介绍
1.1 W 21空间的基础介绍


2 AFD在W 21[a,b]空间的应用
2.1 最佳n 项逼近及其性质




2.2 AFD的最佳n 项逼近收敛性



3 W 21[a,b]空间中的最佳数值原函数



图1 求解的数值积分原函数Fig.1 Solving the original function of numerical integration
