脉冲控制下一类多权重复杂网络的鲁棒H∞同步
2021-04-12郑子钊彭世国付志文徐云剑
郑子钊,彭世国,付志文,徐云剑
(1. 广东工业大学 自动化学院,广东 广州 510006;2. 广东农工商职业技术学院 智能工程学院,广东 广州 510507)
近年来,复杂网络引起了学界越来越多的关注。多变复杂的系统可以用复杂网络加以描述,如神经网络、电力网络、通信网络等。同步作为复杂网络的典型集群动力学行为备受关注,现有相关理论研究已被应用在保密通讯[1]、信号处理[2]、机器人列队[3]等诸多实际领域。复杂网络的同步可以简单理解为网络中或者网络之间的节点系统通过相互作用或外部调控,使状态逐步接近,最后达到同一状态。
在实际应用中,复杂网络不可避免地会受到各种因素的影响,如环境中的外部干扰、通讯时延等,这些因素可以使原来稳定的系统变得不稳定[4]。对于如何衡量外部干扰对系统的影响,鲁棒H∞控制则具有较好的描述与处理方法,其控制思想是把系统输出控制在外部干扰的某一特定范围之内,所以对鲁棒H∞同步的研究尤为重要。文献[5]考虑切换复杂网络的鲁棒H∞同步问题,文献[6]通过分布式脉冲控制方法,得到了时滞复杂网络实现鲁棒H∞同步的充分条件,文献[7]考虑复杂网络的鲁棒H∞有限时间同步问题, 文献[8]在文献[7]的基础上考虑复杂网络结构不确定时的鲁棒H∞有限时间同步问题,需要指出的是,上述文献只针对单权重复杂网络。
现实中,由于复杂网络节点间的连接具有非单一性,如人际网络中,个体间的通讯可以通过网络、电话、传真等多种方式实现。每种方式具有各自的特点,多权重复杂网络可以更精确地描述这类系统的动态特性,即网络的节点间存在多个连接边(权重)。文献[9-12]研究了多权重时滞复杂网络的同步和鲁棒H∞同步问题,文献[13]研究了多权重复杂网络存在自适应状态耦合时的鲁棒H∞同步问题,文献[14-15]通过运用牵引控制方法,得到了多权重复杂网络的实现鲁棒H∞同步的充分条件。
如上所述,已有众多方法用于处理多权重复杂网络的鲁棒H∞同步问题,如反馈控制、牵引控制、自适应控制。在众多控制方法中,脉冲控制作为一种非连续控制,能有效降低控制成本,增强系统抗干扰性能,具有很强的实用性[16]。本文将通过脉冲控制方法考虑一类多权重复杂网络的鲁棒H∞同步问题。受文献[5-6]启发,本文设计了新颖的分布式脉冲控制器,通过在分布式脉冲控制器中添加误差状态反馈项,以保证网络实现鲁棒H∞同步。通过模型变换, 利用Lyapunov稳定性理论分析网络的鲁棒H∞同步特性,以线性矩阵不等式(LMIs)的形式给出了多权重复杂网络实现鲁棒H∞同步的充分条件,仿真结果验证了结论的正确性。
1 问题描述与预备知识




2 主要结果
定理1 考虑满足假设1的同步误差系统式(6)。若对于给定常量0 <μ,0 <ϑ <1, N ×N 维矩阵 M和脉冲时刻序列ζ (ρ) ,存在一个矩阵 P >0 和常量α >0。有下列LMIs式(7)、式(8)成立,则同步误差系统式(6)是全局指数稳定的。





备注3 定理2给出了多权重复杂网络式(1)在受到外部干扰影响时实现鲁棒H∞同步的充分条件,网络的鲁棒H∞同步性能由同步误差系统式(5)的稳定性和 L2-增 益来衡量,γ 值越小, L2-增益越小,网络对干扰的抑制能力越强。
3 数值仿真
本节将对多权重复杂网络式(1)进行数值仿真,验证上述结论的有效性,给定如下参数。
n=3, N =5, g =3, f(t,xi(t))=arctan(t)xi(t),C =[1,0,0],Di=(0.2+(-1)i0.05i)[1,1,1]T。显然,可取L=[2,2,2]使f (t, xi(t))函数满足Lipschitz条件。时变时延 τ(t),0 ≤τ(t)≤0.7, 可知τ ¯=0.7。 节点间耦合强度a1=a2=a3=1。内 部 耦 合 矩 阵 Γ1=diag{0.2,0.1,0.1} ,Γ2=diag{0.1,0.1,0.2} , Γ3=diag{0.2,0.2,0.1},耦合权重矩阵为

进一步,验证定理2的有效性。取脉冲时刻序列{tk}∈ζ(0.03),tk-tk-1≡0.03,k ∈N+。
给定 γ=1.8,ϑ=μ=0.57,δ=1.2,误差反馈增益矩阵 Z=diag{-0.4,-0.4,-0.4,-0.4,-0.4}。根据耦合权重矩阵,设计外部耦合矩阵数随时间变化的曲线如图2所示,可见各节点状态xi(t)渐 近趋向同步状态s (t),网络实现同步。

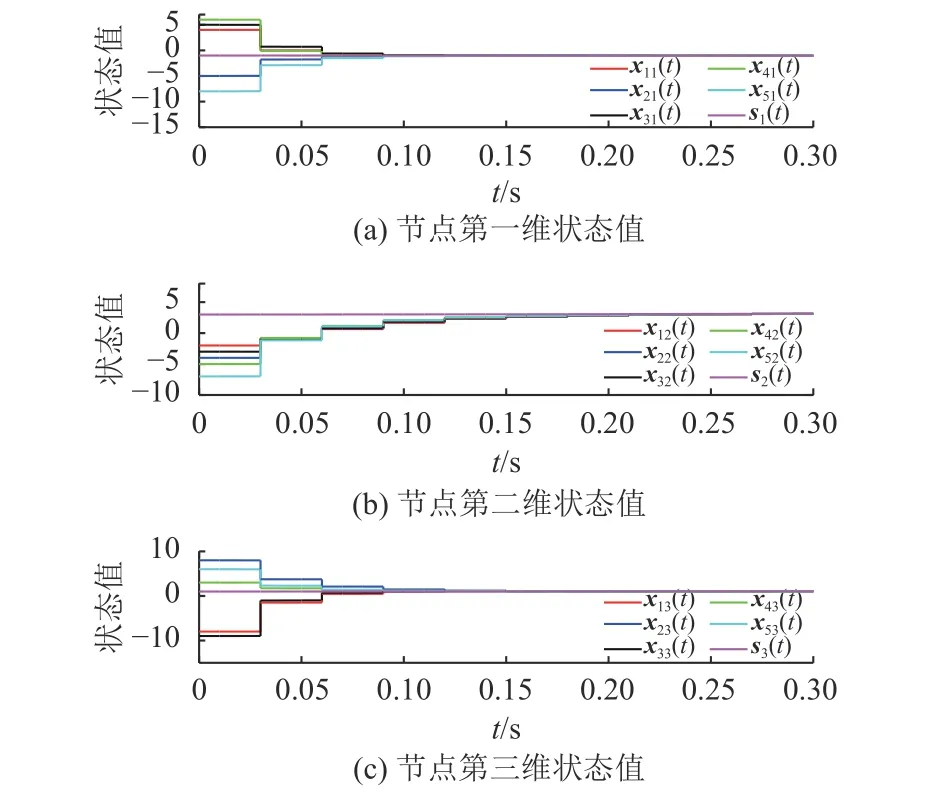
图1 脉冲控制下,网络式(1)各节点状态曲线Fig.1 State curves of each node in the network formula (1) under impulsive control

图2 脉冲控制下,同步误差系统式(4)各节点的状态范数曲线Fig.2 The state norm curve of each node in synchronization error system formula (4) under impulsive control

4 结论
本文基于脉冲控制方法,对一类多权重复杂网络的鲁棒H∞同步问题进行了研究,给出了多权重复杂网络实现鲁棒H∞同步的充分条件,并用Matlab软件实例仿真验证了结论的有效性。研究结果表明,通过在分布式脉冲控制器中添加节点状态变量与同步状态间的误差状态反馈项,可以保证同步误差系统是内部全局指数稳定的且具有有限的 L2-增益,多权重复杂网络实现鲁棒H∞同步。
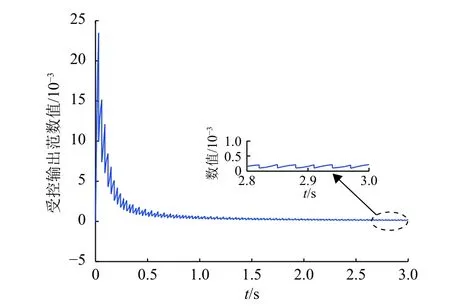
图3 脉冲控制下,同步误差系统式(5)的受控输出范数曲线Fig.3 The controlled output norm curve of synchronization error system formula (5) under impulsive control
