考虑气动效应的索桥耦合参数振动建模及1∶1内共振分析

闵光云，刘小会，张春霞，孙测世，蔡萌琦

（1.重庆交通大学 省部共建山区桥梁及隧道工程国家重点实验室，重庆 400074；2.重庆交通大学 土木工程学院，重庆 400074；3.成都大学 模式识别与智能信息处理四川省高校重点实验室，成都 610106；4.成都大学 建筑与土木工程学院，成都 610106）

覆冰索的舞动一直是一个备受关注的课题［1-13］，为抑制覆冰索的舞动须研究其产生舞动的原因，长时间来经过科研学者们的努力，学术界已经存在三大经典的舞动机理［14-16］。针对覆冰索的动力学研究，学者们的研究对象一般为单档悬索结构，忽略了覆冰索和桥面的相互作用，只研究覆冰索的舞动特性。郝淑英等［8］使用平均法系统地研究了覆冰索的瞬时固有频率，发现舞动幅值对高阶瞬时固有频率有很大的影响，且固有频率存在“飘移现象”，索的档距与风速决定着飘移量的大小。晏致涛等［9］基于增量谐波平衡法推导了单档覆冰悬索的舞动方程，并求得了其舞动方程的解，接着将之与时程积分法所得解作比较，两者结果完美的吻合在一起，验证了增量谐波平衡法所得结果的正确性。刘海英等［10］将覆冰拉索简化为连续体模型，接着基于Mathmatic程序模拟单档覆冰拉索的舞动轨迹图和时间历程曲线，最后与有限元模型的结果相对比，证明了连续体模型能良好地反应拉索的振动特性。朱宽军等［11］通过覆冰拉索的张力变化理论及试验分析，得出了张力变化的规律，结合张力变化对拉索、金具、绝缘子等受力构件的影响，提出了提高覆冰拉索的机械强度，进而防止覆冰拉索舞动的方法。王少华等在文献［11］的基础上建立了覆冰拉索舞动的3自由度数学模型，采用Fluent软件对覆冰拉索的空气动力参数进行了数值仿真，根据舞动引起的拉索长度变化，计算了舞动引起的拉索张力变化，分析了舞动幅值、半波数、档距等参数对张力变化量的影响［12］。

近20年来，随着中国经济的飞速发展，越来越多的大跨越桥梁被建立，而桥梁上的拉索易在覆冰等因素的影响下发生舞动，长时间的舞动会产生严重的后果，进而造成经济损失。尽管越来越多的科研学者们针对拉索的舞动做了深入的研究，但多数学者一般只考虑了单个索的舞动，或者只研究了索桥耦合模型的参数振动，本文在现有研究的基础上建立了索桥耦合振动的参数模型，并考虑了气动阻尼效应对拉索振动特性的影响，本文的研究成果能给予工程一定的指导。

1 索桥耦合动力学建模

为研究索桥之间的耦合非线性参数振动，须建立对应的索桥耦合参数振动模型。图1为索桥耦合参数振动模型，即将桥面理想化为一个质量块，进而研究拉索的索与桥面之间复杂的动力学行为。

图1 参数振动模型

图1中y表示静平衡位置处拉索的抛物线构型，w表示拉索偏离静平衡位置的动态位移，θ表示拉索与水平方向的夹角，K表示桥面的刚度，C表示桥面的黏性阻尼，X为桥面端部的位移。

将拉索当作连续体，根据牛顿定律可得拉索面内的动态平衡方程为

式中：T表示拉索的初始张力；τ表示拉索的动态张力；m表示拉索单位长度的质量；g表示重力加速度；s表示弧坐标。

拉索的重力平衡方程为

将式（2）代入（1）可得

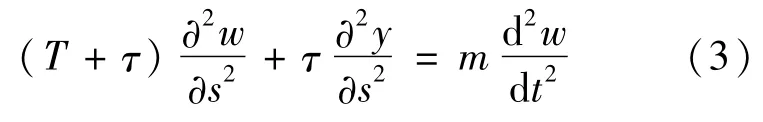
分别在拉索静态平衡构型上与偏移平衡位置的动态平衡构型上取出一微元段，基于该微元段求解拉索的动态张力，见图2。

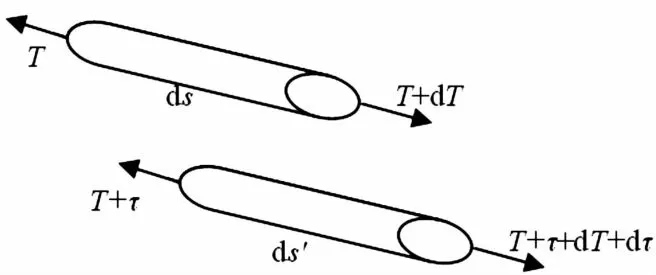
图2 微元段

图2中d s为静平衡构型上的微元段，d s′为动态平衡构型上的微元段。根据上述微元可得拉索单位长度上的动张力的表达式

式中EA为拉索的拉伸刚度。

根据索桥耦合参数振动模型，桥面端部的位移也会影响拉索单位长度上的动张力，因此式（4）转变为

式中l为拉索的跨径。

实际工程中拉索的跨径远远大于其直径，因此拉索轴向的振动很微弱，当忽略拉索轴向的惯性力可将动张力表示为

将式（6）代入式（3），且考虑拉索所受阻力、气动荷载可得

式中：fc表示拉索的阻尼系数；Fair表示拉索所受气动荷载。

2 气动力动力学建模

在冬季季风的作用下拉索的表面会结冰，覆冰会使拉索表面产生一定大小的气动荷载，为分析气动荷载对拉索的作用形式，首先须建立拉索横截面模型，见图3。

图3 覆冰拉索横截面

图3中FL表示气动升力，FD表示气动阻力，α表示攻角，α0表示初始攻角，U表示风速。

可得到

式中：αt为相对风攻角；ρ为空气密度；D为拉索的迎风直径；Cy（α）为气动参数，其表达式根据三次曲线拟合为

式中：α1、α2、α3为待定系数；α为瞬时攻角，且满足

式中θt为拉索的扭转角。

拉索的振动特征主要由基本模态决定，因此基于一阶模态截断法可将动态位移写为

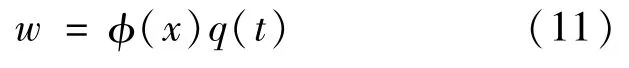
式中：φ（x）表示振型函数；q（t）为振动函数。

将式（8）（9）（10）（11）代入式（7）并结合Galerkin离散法可得

式（12）中系数的表达式分别为

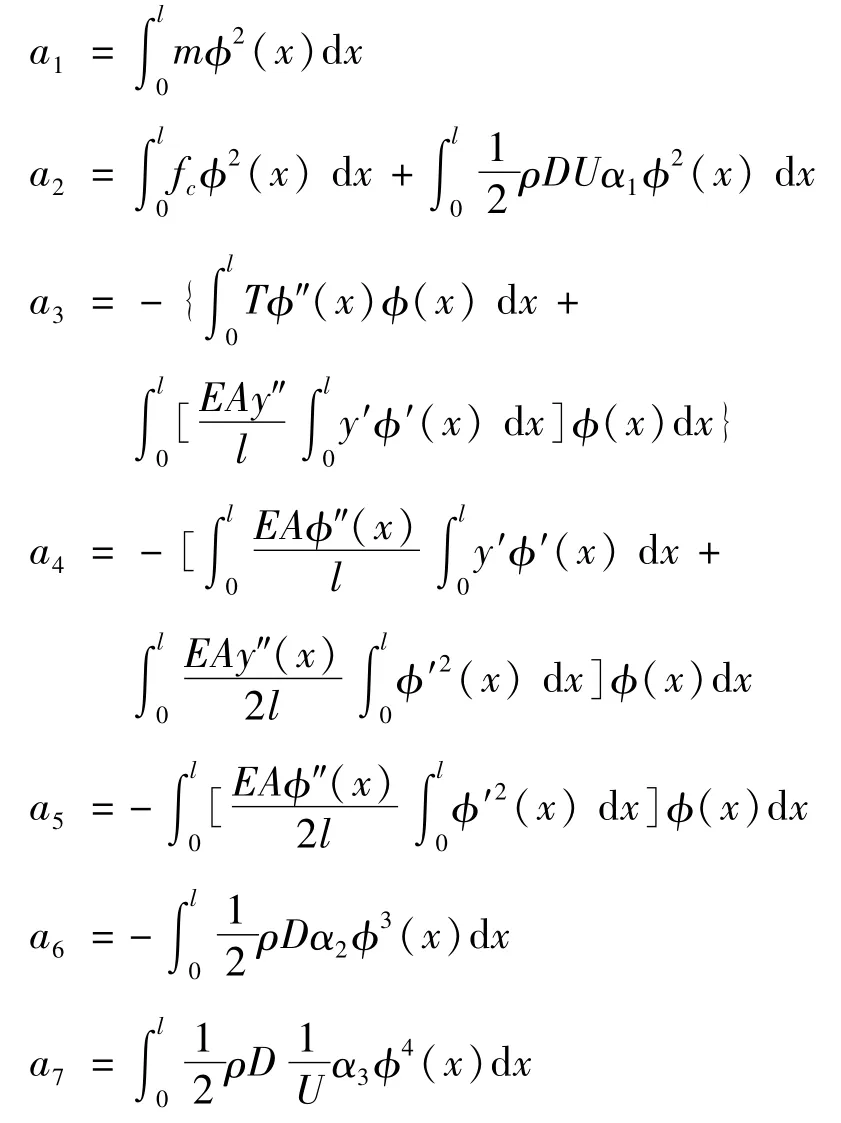
根据牛顿第二定律可得桥面的振动方程为

其中M为桥面的质量。

将式（11）代入式（13）可得

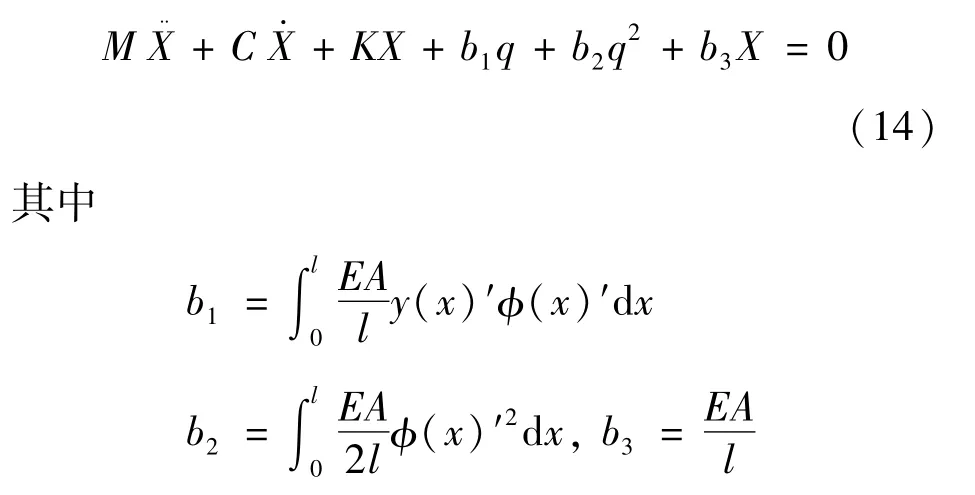
联立式（12）与式（14）可得考虑气动效应影响的索桥耦合振动方程组，即

只要能确定拉索的三分力气动参数，那么就可以基于四阶Runge-Kutta法求解式（15）。

3 多尺度分析

近几十年来，随着非线性振动领域的蓬勃发展，越来越多的求解非线性常微分方程组的定量分析方法被完善，其中多尺度法［17-21］最受学者们的青睐，本文亦使用多尺度法来确定索桥耦合系统可能存在的共振模式。

为便于多尺度法的使用，首先转化式（15）的形式为

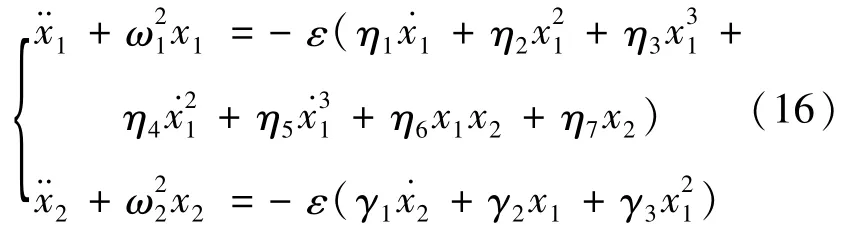
其中ε为量纲为一化的小参数，式（16）涉及的其他参数表达式见下：

将式（16）的解设为

式中：T0、T1表示时间尺度，T0＝t为时间的快变化，T1＝εt为时间的慢变化，x10、x20为索桥耦合系统的周期解，x11、x21为索桥耦合系统的修正解。

将式（17）代入式（16），并按照ε的阶次由低到高整理可得

可将式（18）的解设为

式（20）中的cc表示共轭项。

将式（20）代入式（19）可得

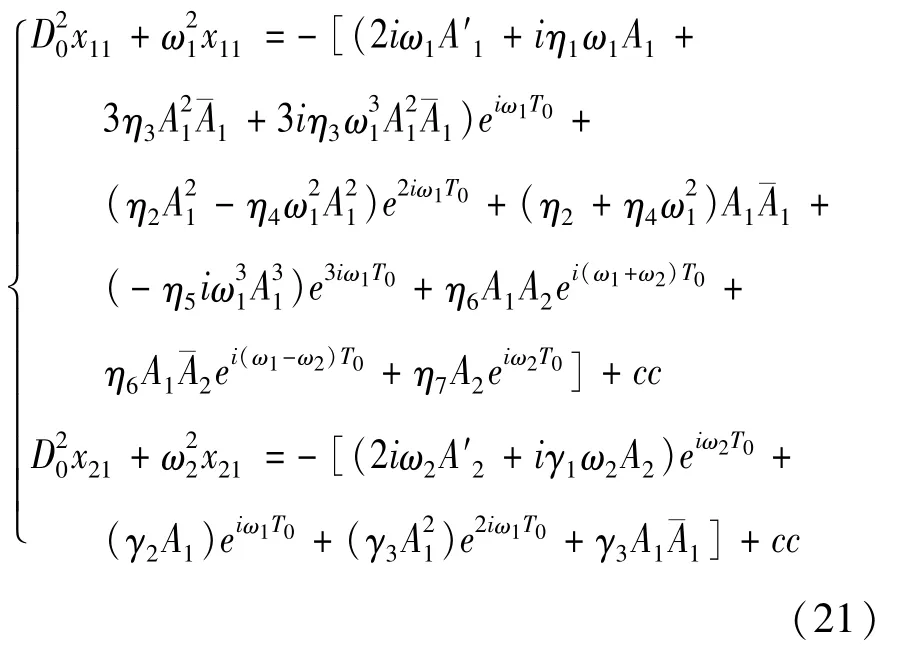
观察式（21）可知索桥耦合共振系统存在ω1≈ω2这种共振模式。

4 算例分析

拉索的拉伸刚度EA＝13.3×106，直径d＝18.80×10-3，张力H＝21.73×103，单位质量m＝1.53 kg／m，y＝（m×g×x×cosθ／（2×H））（lx）。桥面的质量M＝14×105，刚度K＝5×106。当选定以上参数时索桥耦合系统刚好满足1∶1内共振，接着参考文献［22］所得的三分力气动参数，并通过4阶Runge-Kutta可求解得到考虑气动效应的索桥耦合系统的位移响应曲线，见图4。

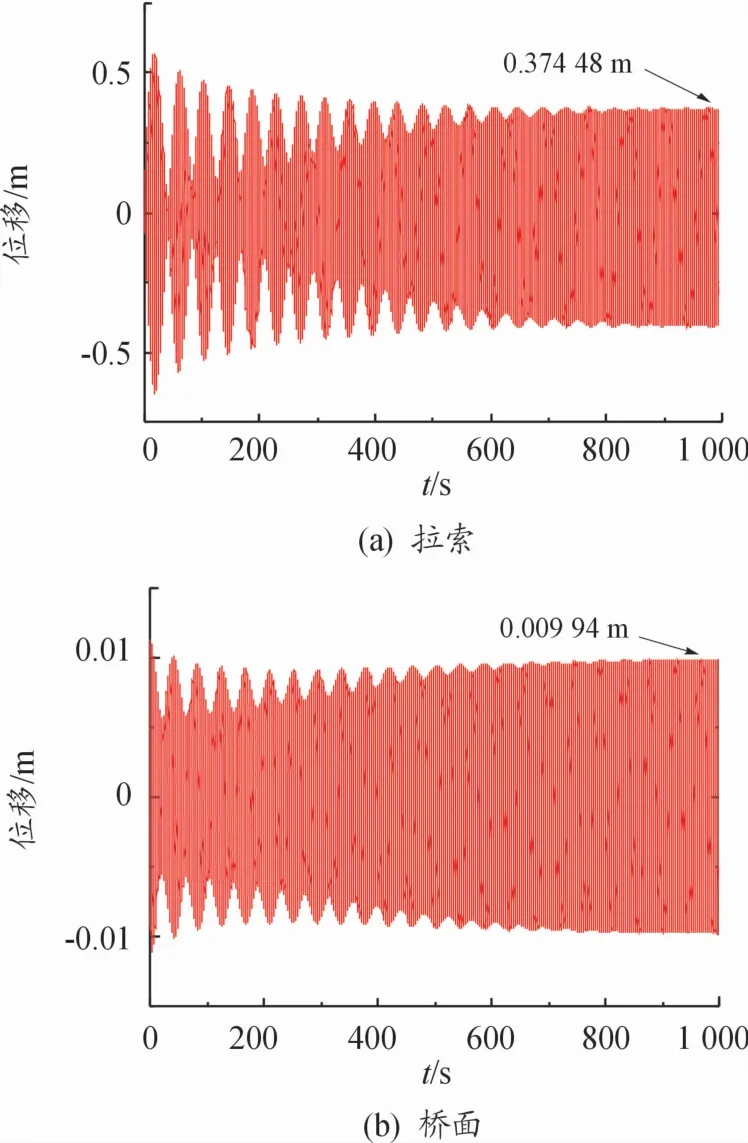
图4 位移响应曲线

通过观察图4可知：800 s之前索桥耦合系统并不稳定，此时因为1∶1内共振的影响，索桥耦合系统的位移响应具有“拍”的特点，能量在索桥耦合系统之间往复传递，当拉索上的能量达到波峰时，桥面的能量就达到波谷，当桥面的能量达到波峰时，拉索的能量就达到波谷；800 s之后索桥耦合系统基本趋于稳定状态，稳定后拉索的幅值大约为0.374 48 m，桥面的幅值大约为0.009 94 m。

图5为索桥耦合体系处于稳定状态后所得的相平面图，桥面、拉索的相平面图都近似为椭圆，这一点与文献［8］所得结论吻合。

下面进一步通过傅里叶变换得到索桥耦合系统的频谱分析图，见图6。

图5 索桥耦合体系的相平面图

图6 索桥耦合体系的频谱分析图

通过观察图6可知：在拉索和桥面的频谱分析图中，该系统在接近1个半波固有频率0.325 Hz处有明显的峰值，表明桥面、拉索的舞动模式皆为1个半波的舞动。

5 结论

通过本文建立的索桥耦合参数振动模型可得：当索桥耦合体系的物理参数满足一定的条件使得其自身能发生1∶1内共振时，索桥耦合体系在800 s之前是不稳定的状态，能量在该体系之间往复传递，桥面上的能量位于波峰时，拉索上的能量刚好位于波谷，且能量具有“拍”的特点，800 s之后该体系逐渐趋于稳定，稳定后其极限环为椭圆形，舞动模式接近1个半波的舞动。