车联网环境下基于间隙优化的无信号交叉口车速控制方法
2021-04-12常玉林张成祥
常玉林,张成祥,张 鹏,孙 超
(1.江苏大学 汽车与交通工程学院,江苏 镇江 212013;2.东南大学 城市智能交通江苏省重点实验室,南京 211189)
随着经济的迅猛发展,汽车保有量的不断提升,交通拥堵及安全问题日趋严重。城市道路网的通行效率取决于交叉口的通行效率,交叉口通畅能力的提升有益于解决交通拥堵。车联网也是近些年研究的热点,车联网环境下的车辆能交互信息,有利于改善传统的交通组织方式。
目前,车联网环境下交叉口控制方法越来越多,Chiara等[1]提出了一种基于启发式算法优化的控制系统设计,能对车辆进行优先级引导,并向驾驶员提供建议行驶车速。Wang Chaojie等[2]在车路协同环境下对车辆的自适应巡航系统进行了优化。Wang Chen等[3]提出了一种交叉口车辆通行最优轨迹控制的集中式协同模型预测控制方法,将最优控制问题转化为具有预测后退约束的离散线性二次控制问题,通过二次规划可以有效地求解,并仿真验证该控制方法能提高交叉口车辆通行效率和能源利用效率。Ban等[4]对自动驾驶车辆的CAV系统进行了研究,发现车联网环境下优化CAV系统的算法有利于减少拥堵。Kopelias等[5]通过逻辑框架和数学分析的方法,研究了车联网环境下车辆的燃油消耗和污染物排放相对于传统交通环境的变化。Mahyar等[6]提出一种协同控制策略,控制车辆在无信号交叉口组成车队和找寻最小安全车头间隙穿行,并验证该控制策略能提高交叉口通行能力。柴琳果等[7-8]提出了一种间隙耦合的无信号交叉口SIs控制方法,通过LOOSE和COMPACT算法优化车队间隙,并对车速进行引导,提出的方法能提高交通效率。Huang等[9]提出一种优化的汽车跟驰模型,考虑了车辆的尾气排放,对车路协同环境的车辆运行系统进行了优化。Navtrre等[10]通过编程算法构建了一个安全评估模块,基于VISSIM对CAV车辆进行行驶安全评估,诱导车辆通行,降低交叉口的冲突。Hao Yang等[11]发展一种先进的无信号交叉口车辆控制系统,该系统提出一种交叉口延误控制模型,用来预测交叉口车辆总延误并寻找交叉口车辆通行的最优速度,通过仿真该系统能降低95%的交叉口车辆延误。Schmidt[12]提出驾驶人个体差异性的预警模型控制车辆通行交叉口,但是该模型算法的运算量很大。当前国外多从基于先进传感器控制车辆通行以及多车协同控制系统、车辆自适应安全驾驶系统等多方面进行研究,国内对传统控制算法进一步改进,特别是在确定无信号交叉口车辆通行权时采用固定的通行规则决定优先权,这种固定车流优先通行的方式不符合公平原则且有可能造成其他方向车流长时间排队等待的现象。
本文提出一种在车联网环境下基于间隙优化的无信号交叉口控制方法,意在解决次路车穿越主路车流交通量较大的无信号交叉口,通过调整主路车队的车头间距,优化主路车的位置,让次路车以较高的合适速度通行,提高交叉口通行效率,降低主路车流延误,减少污染物排放。
1 问题描述
传统无信号主次路相交的平面交叉口,当主路车流量较大时,出现不可穿越间隙,次路车辆到达交叉口时不可穿越主路车流,需减速停车,或者次路车在穿行主路车流时,次路车依赖于驾驶员判断,可能会速度过快或过慢,与主路车发生冲突,从而引发交通事故(图1)。

图1 问题描述示意图
在车联网的环境下,自动驾驶车辆进入交叉口时,可通过V2I、V2V技术获取周围几乎所有车辆的速度、位置、行驶轨迹等交通信息,通过这些交通信息可以预测次路车在穿越主路车时,两车是否会发生碰撞,或者存在不可穿越间隙。若出现车辆碰撞的情况,可以引导次路车以一个安全速度区间行驶穿越,避让主路车。若主路车之间形成不可穿越间隙时,主路车应该调整自身车速,形成可穿越车头间隙供次路车穿行。
2 无信号交叉口车速控制方法
2.1 控制策略
当车辆进入控制区域时,主次道路所有车辆的位置、速度、航向角、行驶轨迹等数据均可获得。当次路车刚进入控制区域内时,根据次路车轨迹、速度、位置,可以预测并判断次路车是否可以通过车流量较大的主路。为了让次路车更快地通过交叉口,次路车可以加速至较高合理的车速vmax(合理的最高车速限制为道路限速和不与该次路前车碰撞的速度),预测并判断是否会与主路车发生冲突或者是否可以穿越主路车流,即是否存在可穿越车头间隙。若次路车可以以较高合理的车速通过,则次路车以该车速直接穿越主路;若不可以通过,则需要调整主路车队的车头间隙,让主路车形成可穿越车头间隙并且避让次路车,让次路车较快通过交叉口。其中图2为控制优化示意图,图3为控制流程图。

图2 控制优化示意图

图3 控制流程框图
2.2 控制模型
2.2.1 次路车控制模型
假设次路第i辆车刚进入交叉口控制区域时,会将次路车的位置、初速度、航向角、目标车道等信息发送给交叉口中心控制器进行预判[13]。控制器会选取一个驾驶员普遍感觉舒适的加速度aci,以该加速度加速至最高车速vimax后匀速行驶到达交叉口时,次路车的行驶轨迹是否会与主路车流发生碰撞,或者在冲突点(主路车流轨迹与次路车轨迹的交点)处是否存在可穿越车头间隙供次路车通过。若能通过,则以较高合理的车速通过交叉口,这样次路车行驶时间最短;若不能通过,则要对主路车队的间隙进行优化。
次路车控制模型的目标函数为次路车到达冲突点的时刻最小,其表达式为

该模型的约束条件有:
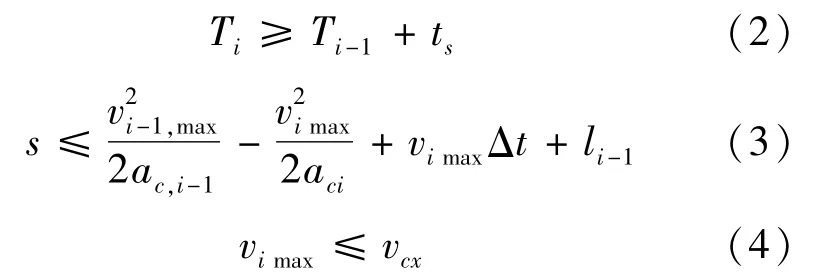
式中:Ti为次路第i辆车到达冲突点的时刻(s);Lc为次路控制区域起点至冲突点的距离(m);aci为次路第i辆设定的加速度(m/s2),依据Yi等[14]以及《汽车理论》[15]所提出的加速度建议值,设定加速度的区间为[-8,2.5](m/s2);Ti-1为次路第i-1辆车到达冲突点的时刻(s);ts为最小车头时距(s);vi0为次路第i辆车到达控制区域时的初速度(m/s);s为前后车之间的安全间距(m);Δt为反应、机械延误等损失时间之和(s),一般取0.3~1.0 s;li-1为次路第i-1辆车的车辆长度(m);vcx为次路的道路限速(m/s)。
若次路车是左转、右转通过交叉口时,需要对最高车速进行进一步约束,即最高车速小于临界转弯车速,约束条件为:

式中:k1和k2为考虑车辆转弯临界车速的参数,k1取决于车辆质量、车辆离心高度、道路状况等相关参数,一般取0.6,k2是提高驾驶安全的安全优化系数,一般取0.3;μmax为最大静摩擦系数,一般取0.9;g为重力加速度(m/s2),取9.8 m/s2;R0为道路转弯半径(m)。
2.2.2 主路车队控制模型
对于主路车而言,当次路车进入交叉口时,以较高合理的车速vimax行驶至交叉口时预测会与主路车流发生冲突,要对主路车流进行间隙优化。
次路车以最高车速vimax行驶至交叉口时预测会与主路车流发生冲突的车辆记为主路车流间隙优化车队的“头车”a1,以初始速度vi0进入交叉口预测会与主路车流发生冲突的车辆的后一辆车记为主路车流间隙优化车队的“尾车”am。将“头车”与“头车”中间的所有m-2辆车记为间隙优化车队,记为集合W。

车辆间隙优化是对集合W进行优化,即保证发生冲突的主路车队的前两辆车能让次路车安全通过,其余的车辆只要保证车辆间安全,按顺序通行即可。所以对车队进行位置优化,优化后的位置能满足“头车”和“头车”后一辆车产生可穿越车头间隙,后面车辆间隙为安全间隙即可,所以车队将从初始状态调整至目标状态,目标状态包含了位置、时间约束、加速度。

式中:daj表示车辆aj距离冲突点的初始距离(m);vaj表示第aj辆车的速度(m/s);Daj表示车辆aj的目标状态距离冲突点的距离(m);T0表示时间约束条件(s);aaj为第aj辆车优化的加速度(m/s2)。
车队的优化时间即时间约束条件由“头车”决定,视“头车”做以加速度aa1先匀加速后匀减速的运动,时间T0定义为
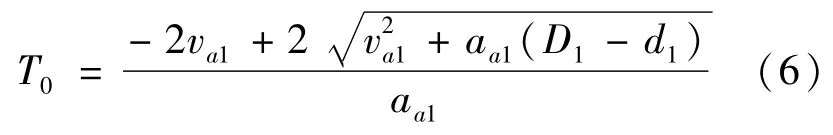
其他车辆的运行过程为以加速度aaj做先匀减速后匀加速的运动,每辆车加速度的定义为

式中:vaj0为车队中第j辆车目标位置优化前的初速度(m/s)。
间隙优化的约束条件为

式中:w为次路车的宽度(m)。
集合W总的车头间距S为

考虑主路车队不能一直以较高加速度进行间隙优化,兼顾环保,将燃油消耗和污染物排放在S的基础上运用经典VT-Micro模型[16]进行综合优化:

式中:My,aj(k)为第aj辆车的污染物排放量和油耗量(L/s);Py为系数矩阵,根据橡树岭国家实验室的实验数据获得;y为CO、HC、NOx排放和燃油消耗等因子,CO取0.866,HC取0.429,NOx取0.273。
主路车队控制模型的目标函数为

式中:Z为主路车队的总模型;η为权重,0<η<1,经过多次实验得η取0.75时优化效果最佳。
2.2.3 次路车车速优化
主路车队优化至目标位置后,需要再次判断次路车是否与优化后的车辆发生碰撞。因为在间隙优化的过程中,车队“头车”需要与前一辆车保持安全车距,就有可能出现碰撞的情况,所以针对这个情况对次路车最高车速进行车速调整。本文通过车辆质点、圆、矩形碰撞模型(图4),将车与车碰撞视为矩形与矩形的碰撞,求解得到更为精确的优化车速。

图4 车辆质点、圆、矩形碰撞模型示意图
次路车降速后不能与“头车”的后一辆车发生碰撞,所以车速的最低阈值为:
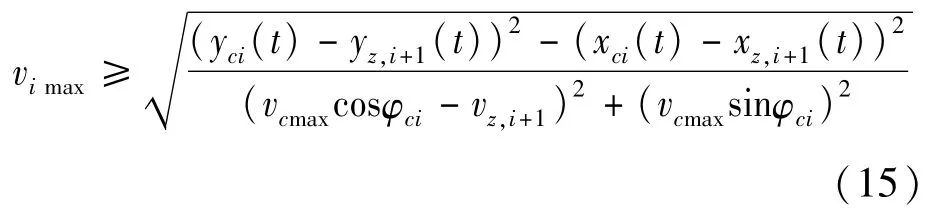
车辆间冲突分为交叉冲突和合流冲突,见图5所示2种情况下次路车车速的最高阈值不同。

图5 车辆冲突示意图
合流冲突(车辆合流时次路车不与主路车碰撞的最大速度上限值):
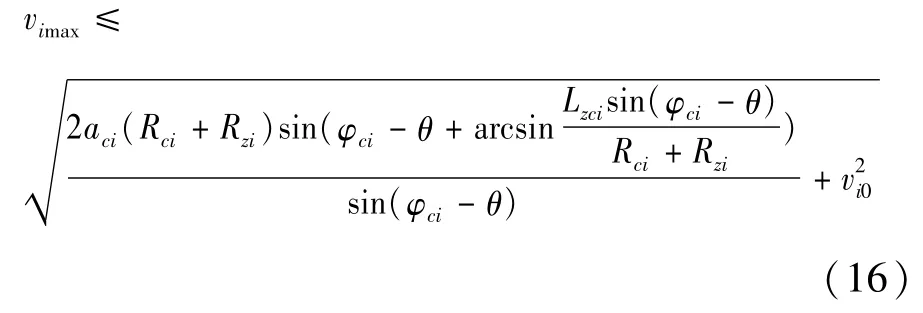
交叉冲突(车辆交叉时次路车不与主路车碰撞的最大速度上限值):
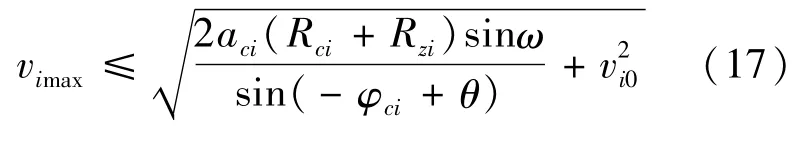

式中:Lzci为预测主路车流中会与次路第i辆车碰撞的车与次路第i辆车之间的直线距离(m);θ为以预测主路车流中会与次路第i辆车碰撞的车的质心为端点,该车的速度为正方向,该车次路第i辆车与连线与正反向的夹角;φci为次路第i辆车进入交叉口控制区域时的航向角;Rci、Rci为车辆的最大对角线的长度(m);(xi(t),yi(t))为第i辆车在t时刻的位置。
2.3 模型的求解过程
基于间隙优化的车速控制模型的求解流程如图6所示。

图6 模型求解流程框图
车速控制模型的求解过程为:
1)次路第i辆车刚进入交叉口控制区域时,判断以较高合理的车速vimax及车辆的行驶轨迹是否与主路车流发生冲突。若不冲突则直接以较高合理的车速通过主路车流;若发生冲突,根据次干路模型及相关约束条件求解Ti。
2)根据较高合理的车速vimax及次路车进入交叉口控制区域时的速度vi0以及根据主路车辆的交通信息,得到优化车队集合W。
3)根据主路车队总模型及相关约束条件计算W的最佳车头间距Daj-Daj-1及车队的加速度aaj,依据Daj-Daj-1、aaj调整主路车队。
4)判断次路车以最高车速vimax是否会与优化后的主路车队发生冲突,若不会,次路第i辆车通过主路车流;若会发生冲突,根据式(15)(16)(17)(18)调整次路车车速,让次路第i辆车降速通过优化的间隙。
5)当下一辆次路第i+1辆车进入控制区域时,重复上述步骤。
3 仿真分析
为了验证本文提出的基于间隙优化的无信号交叉口车速控制方法的有效性和正确性,运用VISSIM仿真软件进行仿真。选取江苏省苏州市中新大道与方中街交叉口,在VISSIM中构建该主次道路相交无信号交叉口,选取交叉口800×400 m的范围作为交叉口控制区域。交叉口主路为东西向,双向2车道,进口道拓宽为1左转1直行1右转;次路南北向,进口道均为1直左1直右。主路的道路限速为60 km/h,次路的道路限速为40 km/h。交叉口通过交通调查发现各车道组的进口道参数如表1所列。依据表1从传统环境下的无信号交叉口和车联网环境下的无信号交叉口进行仿真比较。

表1 交叉口进口道车辆构成比例
3.1 主路通行能力对比分析
通过VISSIM仿真中放置在东西进口主路直行和左转的车辆检测器,仿真得出如图7所示的通行能力。

图7 传统驾驶和车联网环境下东西进口道通行能力
根据图7可以看出,本文提出的基于间隙优化的车速控制方法能有效提升主路通行能力。车联网环境下的控制策略相对于传统驾驶环境,东进口通行能力提升10.45%左右,西进口通行能力提升17.28%,通过间隙优化,主路车流会尽量缩短至安全车距,压缩车队,提高通行能力。但是随着次路车流的不断提高,主路车流也相应的受到干扰而降低。
3.2 污染物排放和污染物排放对比分析
燃油消耗和污染物排放信息通过经典的VTMicro模型[16]计算得到。根据该模型,仿真得出具体的燃油消耗和污染物排放量,如表2所示。

表2 2种驾驶环境下单位时间车辆的燃油消耗和污染物排放量
根据表2计算得出,在车联网环境下运用基于间隙优化的车速控制策略,单位时间内的燃油消耗量降低了21.6%,CO排放量降低了59.8%,HC排放量降低了49.3%,NOx排放量降低了73.9%。本文提出的控制方法,车辆在控制区域内的车辆能有效降低交叉口的污染物排放,减少燃油的消耗。
3.3 交叉口平均行程时间对比分析
通过VISSIM仿真,得到的结果见图8,当次路交通量从100 veh/h增加到500 veh/h时,传统驾驶环境下的交叉口平均行程时间曲线一直在车联网环境下的交叉口的上方,且相距较大。由于仿真时只改变交叉口的控制策略,所以车联网环境下的无信号交叉口行车会更快。车联网环境下无信号交叉口4个进口道平均行程时间相对稳定,时间变化基本保持在2 s左右。依据表3所示数据,车联网环境下无信号交叉口车辆的车均延误随着次路交通量从100 veh/h增加到500 veh/h较传统驾驶环境降低10 s左右,且交叉口平均行程时间也减少10 s左右。车联网环境下的交叉口平均行程时间较传统环境提高44.43%,平均行程时间减少8.44 s,车均延误降低58.49%,交叉口的通行效率提升。

表3 2种环境下交叉口平均行程时间和车均延误

图8 2种环境下4个进口道平均行程时间
本文的控制方法对于保障车辆通行安全、降低交叉口污染物排放、提高交叉口通行能力和通行效率方面优于传统环境下的无信号交叉口。
4 结语
1)车联网环境下基于间隙优化的无信号交叉口控制方法,能有效提高次路车穿越流量较大的主路,而且能提升主路的通行效率,降低交叉口污染物排放和车辆的燃油消耗。
2)基于间隙优化的车速控制方法能提升次路通行车速,压缩主路车队,起到次路车“见缝插针”式的通过交叉口,提高交叉口整体的通行效率和平均行程车速。
基于间隙优化的无信号交叉口车速控制方法仍需要进一步扩展到考虑车辆换道及超车的情况,从而建立更符合实际车辆运行状况的交叉口控制模型。
