基于CORS定位的无人驾驶路径跟踪研究

高伟健，储江伟，管湘源

（东北林业大学 交通学院，哈尔滨 150040）

无人驾驶车辆是未来的车辆发展方向。无人驾驶车不仅仅是某个领域的成就，还集成了机械、自动控制、计算机科学以及人工智能等众多领域的先进技术。目前的无人驾驶车依靠摄像头（单目和双目）、激光雷达等一系列的设备进行环境感知，特别是三维激光雷达，高昂的成本难以让大众接受，也给普及无人驾驶车带来极大阻碍［1-2］。因此，寻找低成本的传感器和辅助设备的方案才是发展无人驾驶车的必由之路。

高精度定位问题一直是无人驾驶车面对的最基本的问题。现在的定位技术多种多样，主要分为室内定位［3-4］和室外定位［5］，本文中关注室外定位技术。室外定位技术主要是GPS和BDS的卫星定位法以及现在大力开发的基于高精度地图的SLAM（同时定位与地图构建）［5］。GPS定位是世界上最早的定位系统，发展至今，民用定位精度仍然停留在米级，国内的BDS卫星定位精度大部分也停留在米级［6］。上述2种技术定位精度不足以满足户外无人驾驶车的需求。基于高精度地图的SLAM可以满足无人驾驶车要求的厘米级定位，但其高精度地图的绘制需要花费大量的人力、物力和财力，并且需要巨大数量的详细数据计算［7］。随着GPS和DBS卫星定位系统的不间断发展和建设，以及CORS（continuous operating reference station）网的建设，现有的载波相位差分技术的发展，目前可以轻松实现厘米级的定位精度，特别是随着接收机关键技术发展和基站的广泛建设，接收机设备价格便宜，定位精度种类繁多且应用范围广。

路径跟踪是无人驾驶车的核心技术之一，路径跟踪是指无人驾驶车根据预先规划出的路径进行安全行驶，最终到达目的地［8］。我国工程院郭孔辉院士于1982年提出了预瞄-跟踪系统理论［9］，建立了驾驶员预瞄最优曲率模型，还对不同的方向控制驾驶员模型进行了比较。目前有很多研究人员加入其中并对无人驾驶车路径跟踪进行更深入的研究，特别是对驾驶员模型的深入研究。这些驾驶员模型应用模糊数学及现代控制理论描绘人的驾驶操作行为，能够反映出人的部分思维能力，特别是模糊神经网络驾驶员模型的提出［10-11］，在很大程度上能够得出人的思维能力，来更优、更完善地对无人驾驶车进行路径跟踪控制。

上述的路径跟踪都是基于驾驶员模型和相应算法结合达到最优的路径跟踪控制，还有一种是将RTK-GPS接收器和IMU传感器在开放的调控中自主导航的轨迹信息转换成无人驾驶车的运动状态量实现路径跟踪［12-13］。

为了更好地提高无人驾驶的定位精度以及路径跟踪的精度，尽量降低各种额外传感的成本［14］，本文中提出了基于CORS网的GPS和DBS卫星定位的无人驾驶车的路径跟踪研究。利用定位系统设备测量规划轨迹，对比测量轨迹和规划轨迹之间产生的误差，把测量轨迹数据量传输给无人驾驶车，观测无人驾驶车实际运行轨迹，验证整体方法的可靠性。

1 大地坐标与空间直角坐标转换

1.1 大地坐标系的选取

大地坐标系是在大地测量中以参考椭球面为基准面建立起来的坐标系。地面某点A的位置用大地经度L、大地纬度B、大地高度H表示。本文中采用建设10年左右的2000国家大地坐标系（China geodetic coordinate system 2000）［15］。

1.2 地球模型及坐标转换

地球是个近似的椭球体，大地平面凹凸不平整，采用CGCS2000参考椭球为第一等位的椭球，CGCS2000参考椭球的定义常数是［14］：

长半轴a＝6 378 137 m，

短半轴b＝6 356 752.314 1 m，

地球扁率f＝1／298.257 221 01，

地球的地心引力常数GM＝3.986 004 418×1014m3／s2，

地球角速度 ω＝7 292 115×10-11rad／s。

如图1所示，CGCS2000大地坐标是以地球质心O为大地坐标的原点，以长半径为Y轴、旋转轴为Z轴所建立起来的空间之间坐标系。可以测出点A经度、纬度和高度（L、B、H），通过下列转换公式可以得出（X、Y、Z）：

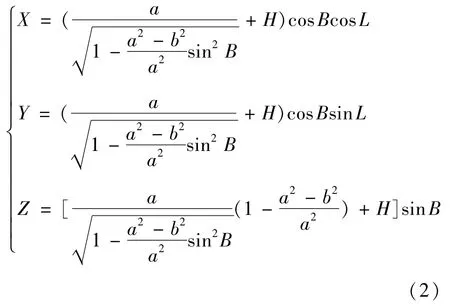
图1 CGCS2000椭球体模型示意图

2 测量方式不同的定位数据分析

采用GPS和BDS卫星定位2种卫星定位融合系统进行测量。网络CORS在国内的发展极为迅速，但其发展过程中存在标准不统一、缺少统一管理等问题。目前，由中国兵器工业集团和阿里巴巴集团共同开发，在全国范围内建立2 200多个地基增强站以及自主定位算法，使全国形成一张网，为农业、汽车业等行业提供高精度定位及高效工作效率。本文中采用 “千寻知寸-FindCM”服务进行定位测量。数据测量整体思路是从点开始分析，再对线分析，最后实现整体规划路径分析。

2.1 测量点数据分析

基于网络CORS的GPS和DBS定位服务主要还是以DBS卫星为主，因为此定位方式得出的定位值（B、L、H）基本都是在浮动值和固定值之间随时变化。为了克服这种变化带来的测量误差，对一点的测量次数在500～800左右。根据不同的时间段、不同的天气等情况进行观察，用均方根（root mean square，RMS）公式拟合最终此点的定位精度［16］。

均方根公式为：

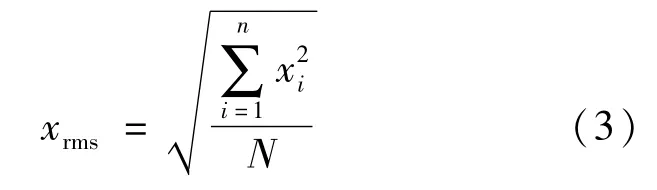
式（3）能在一定程度上反映测量值的优劣，认为RMS值越小越好。再根据定位水平精度因子（HDOP）评价2种卫星定位融合系统的定位精度及定位误差，水平精度因子数值越大代表精度越差，数值越小代表精度越高。

2.1.1 未连接CORS网络测量点分析

利用上述公式对数据进行初步处理，选取RMS较小值的点进行数据对比分析，如图2、3所示。图2、3表示未连接CORS网络定位数据。图2中的A、B、C、D不同形状点代表在1 d时间内、不同时段对地面同一点的测量，可以清晰地反映出测量值与预估值之间的浮动误差约1 m。

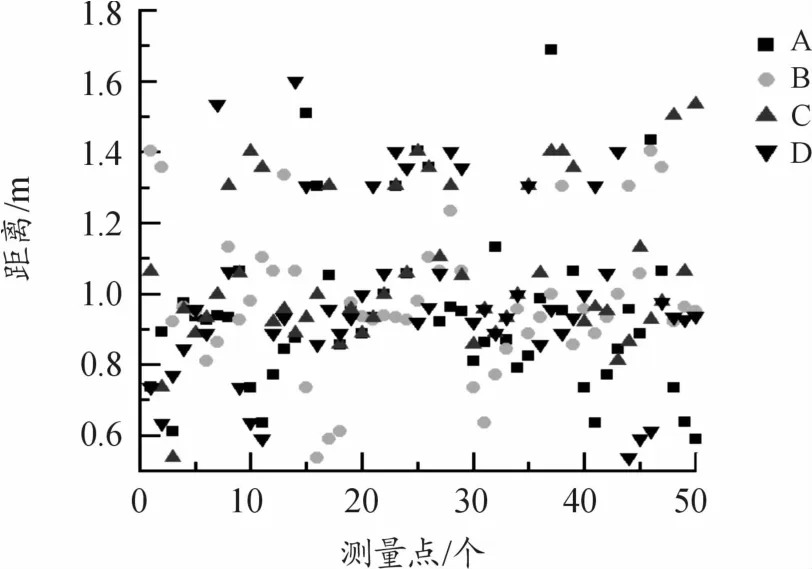
图2 测量值与预估值

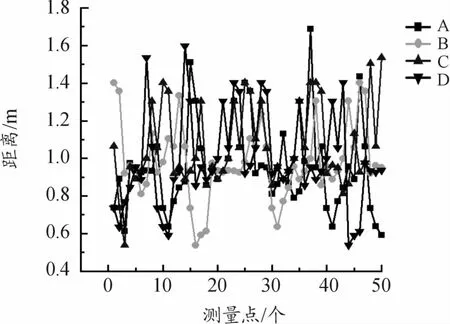
图3 测量值与预估值波动

2.1.2 连接CORS网络测量点分析

利用上述公式对数据进行初步处理，选取RMS较小值的点进行数据对比分析，如图4、5所示。图4中可以清晰地反映出测量值与预估值之间的浮动误差基本在25 cm以内，一些测量点的测量值与预估值间的偏差距离过大，但偏差距离大的测量点对整体测量结果影响不大。图5中的数据反映在1 d内、不同时间段对同一点的测量波动情况，可以充分反映出测量点与预估点之间的跳跃程度，从图中看出并未出现距离突然增大点，表明其稳定可靠。

通过试验分析连接CORS网络定位数据和未连接CORS网络定位数据时的情况对比，可以清晰得出，连接CORS网络定位可以提高4～5倍的定位精度，且定位设备工作稳定。

图4 测量值与预估值

图5 测量值与预估值波动

图4、5仅对测量点和预估点之间距离和波动情况做出详细分析，并未得出具体的测量点相对预估点的具体位置和方位信息。本文中将利用二维高斯投影坐标公式（5）来确定测量点相对于预估点的位置信息［17］：

式中：Sm为纬度B对应的子午线弧长（m）；η2＝

利用上述公式可以绘画出测量点和预估点之间的具体位置和方位图，如图6所示。

图6 测量值与预估值方位

2.2 测量点形成测量轨迹

通过对测量点的详细分析可以得出测量点和预估点之间的误差距离，也可以得出测量点和预估点之间的相对位置和距离信息。通过对一条直线进行分点测量，对直线中预估点进行测量来形成测量轨迹。测量轨迹偏差分析如图7所示。

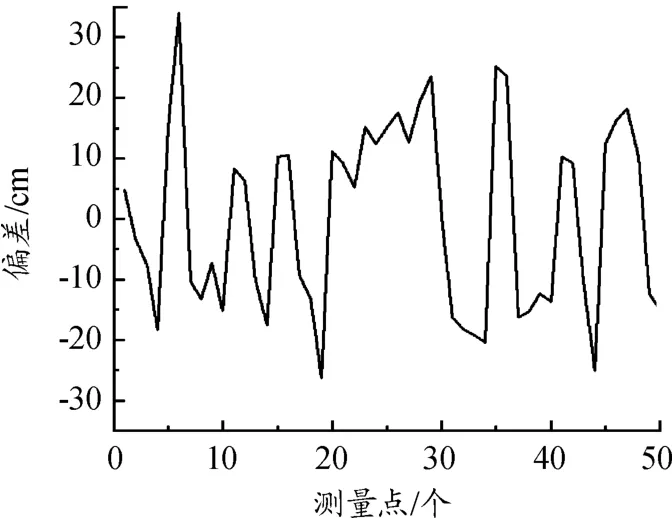
图7 测量轨迹偏差

图7中负值代表测量轨迹偏差在直线左边，正值代表测量轨迹偏差在直线右边。从图7中可以得出，测量轨迹单侧偏差在30 cm以内。通过多次测量对比总结规律得出更为准确的偏差区间，此偏差区间作为仿真实验路径跟踪研究的反馈信息，可进一步提高路径跟踪的精度。

3 基于运动学自行车模型的仿真控制

对于汽车运动的描述极其复杂，故采用自行车模型（bicycle model）作为一种有效的车辆运动化简方式，应用到仿真中。利用python语言实现车辆控制及点追踪的跟踪。

3.1 车辆运动学自行车模型

运动学自行车模型可以简化汽车运动状态，是最有效、简单的方式。如图8所示，为运动学自行车模型示意图。

式中：（xt，yt）为车辆当前的（x，y）坐标；（xt+1，yt+1）为车辆下一时刻的（x，y）坐标；vt为车辆的速度；φt为车辆当前的偏航角；lf和lr分别为前轮和后轮到车辆重心的距离；θf为车辆前轮转角，由于大部分车辆后轮不带转向功能故θr＝0。

图8 运动学自行车模型示意图

根据上述运动学自行车模型，利用PID控制实现自行车模型的横向和纵向控制。轨迹的设定利用能够带有直线和弧线的400 m标准跑道。车辆预瞄点设置为提前两点，车辆到达目标点的半径阈值根据测量的具体误差进行调节，利用python中的numpy数据进行车辆运动状态的运算。

3.2 仿真实验数据分析

应用PID控制实现自行车模型的点追踪仿真实验，在控制车辆速度不同的情况下分析点追踪误差和调节不同的目标点的半径阈值对跟踪误差的影响。车辆跟踪的路径信息用GPS／BDS连接CORS网络进行定位测量而出，形成类似于标准400 m跑道图形，此路径信息是通过测量大约120个定位点而形成的。如图9所示，为40 km／h点追踪图。

图9 40 km／h点追踪

根据图9的40 km／h的点追踪图和利用均方根求出的车辆到达目标点和规划点的误差值，如图10所示。

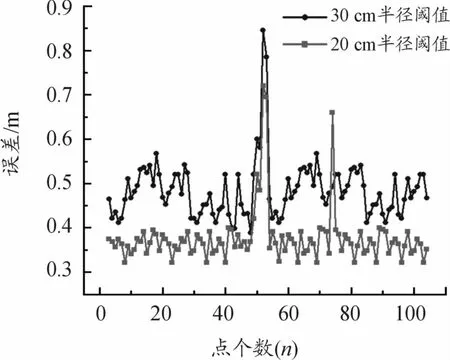
图10 40 km／h的点追踪误差

根据图9，车辆起始点在曲线点（2，0）位置，经过2个点之后，车辆就回归在预定的路径点上，证明车辆横向PID控制器在一段时间后开始起作用，车辆在纵向PID的控制下也将车速控制在40 km／h的时速下，车辆按照规定的目标点进行有规划的行驶，但可以看出车辆在转弯处时到达的点和预定的目标点之间产生偏差，根据图10可以清晰地看出半径阈值为30 cm时，车辆在转弯处的最大误差值在0.85 m，而在直线的误差值最大0.54 m，其余的直线误差值在0.45 m左右。在半径阈值20 cm时，车辆在转弯处最大误差值在0.75 m，在直线的误差值最大值为0.48 m，直线的平均误差值在0.4 m左右，在两者相对比下在不同的目标点阈值下车辆跟踪误差有所差别。不同的目标点阈值设置是为了模拟CORS网络的差分定位，通过仿真实验得出在30 cm半径阈值和20 cm半径阈值下，半径阈值设置的相对小能够提高车辆跟踪误差精度，由于GPS定位精度的限制，目标点半径阈值的设置需在一个可控的范围内。

图11为50 km／h点追踪图，从图中可以明显看出车辆在转弯处产生的误差相对较大，在直线线点的跟踪误差也会相应增大。图12为50 km／h点追踪误差图，车辆在转弯处的最大误差值在1.42 m，而在直线的误差值最大0.56 m，其余的直线误差值在0.5 m左右，在不同的半径阈值下车辆的跟踪精度相对提高了7 cm。但在车辆转弯处的横向PID控制的控制参数相对不满足当前的车速设定，造成车辆跟踪精度下降，对于PID控制的3个参数需要多次重新调节来适应相应的车速增加，达到相对理想的车辆跟踪精度。

图11 50 km／h点追踪

图12 50 km／h的点追踪误差

4 结论

基于CORS网络定位的无人驾驶路径跟踪，通过GPS点定位精度分析到整条路径误差分析的思路，通过大量实验得出CORS网络定位精度能够提升4～5倍，定位精度稳定且定位设备工作可靠。在车辆横向、纵向PID控制方面都具有一定的效果，使路径跟踪误差控制在0.6 m，整体误差比较合适。通过不同车速相同半径阈值的对比，车辆行驶速度的增加导致车辆横向控制难度增大，造成路径跟踪误差增加，也可能速度到达一定值时PID控制失去作用。在相同车速不同的半径阈值设定情况下，半径阈值的减小会提高车辆跟踪精度。

应用CORS网络定位提升了定位精度和路径跟踪精度，但存在一些问题，还需要进一步的理论与试验研究。寻找出更有效果的控制算法以及采用多频段、多通道、处理性能更高的RTK定位设备，搭建小型的无人驾驶车辆进行试验，改进理论控制算法，提高路径跟踪精度。