基于人机共驾的车道保持驾驶辅助系统

张新锋，左 思，田圣哲

（1.长安大学 汽车学院，西安 710064；2.汽车运输安全保障技术交通行业重点实验室，西安 710064）

汽车工程师协会（SAE）将自动驾驶技术分为6个级别（L0-L5）［1］，其中L5等级最高，能实现任何道路交通环境的完全自动驾驶，但从实际应用的角度来看，目前无人驾驶技术还不成熟。由无人驾驶车引起的交通事故屡屡发生，法规也尚未明确无人驾驶技术引起的事故责任应由谁承担。此外，复杂的道路交通环境［2］也决定了无人驾驶技术在短期内难以实现，这便促进了汽车安全辅助驾驶技术（ADAS）的研究。

BOSCH公司研发的车道保持驾驶员辅助系统通过摄像头探测前方车道的界限，在未打转向灯却有越界危险时警告驾驶员［3］。奔驰的LKA系统利用挡风玻璃内侧的摄像头监控道路标记，并检测车辆是否离开车道，该系统还可以评估驾驶员的动作，确定汽车是有意还是无意离开了车道。如果驾驶员在超车或驶入高速公路之前加速，严重刹车或转向弯道，则不会进行干预［4］。

柳长春等［5］利用模型预测控制器获得矫正转向角，但未考虑驾驶权限分配问题，易造成人机冲突。Sterling J.Anderson［6］根据实际行驶路径和目标路径之间的偏差自适应调整共驾系数k来辅助驾驶员完成任务，但不能保证驾驶员始终处于人机控制系统中，导致驾驶员失去对车辆的最终控制权。罗莉华等［7］研究车辆的侧向动力学，设计了转向控制策略，但未进行汽车稳定性控制，容易发生侧翻。

基于以上结论，本文中建立了一种人机共驾的驾驶辅助系统，该系统能够实现驾驶员和控制系统同时执行驾驶任务（L2-L3），提高汽车主动安全性，减少交通事故的发生。在驾驶员的基础上，建立了辅助控制系统的控制目标、机械结构约束和横摆稳定性约束，最后搭建Simulink与CarSim联合仿真平台，设计不同行驶工况，对辅助驾驶系统的控制效果和鲁棒性进行仿真验证。

1 参考模型

1.1 驾驶员转向行为模型

驾驶员操纵车辆跟踪车道中心线主要通过转向、制动和决策等［8］驾驶行为来调整车辆的横向位置，而车辆的无意识偏离大多是由于驾驶员注意力不集中导致转向操作失误所引发的，所以本文主要对其转向行为进行研究。基于驾驶员在驾驶过程中习惯将目光集中于前方一点处预估车辆当前位置至道路中心线的侧向偏差的驾驶行为特性，采用单点预瞄模拟驾驶员的转向行为。如图1所示，经过预瞄时间Tp后，在预瞄点处车辆相对于车道中心线的位置偏差为：

式中：在大地坐标系OXY下，vy为横向速度；y（t）为当前时刻的车辆侧向位移；f（t）为车道中心线方程；f（t+Tp）为经过预瞄时间Tp后的期望侧向位移。

图1 单点预瞄运动分析示意图

驾驶员的驾驶目标是通过控制前轮转角减小侧向位置偏差es，使汽车在经过预瞄时间Tp后，其实际横向位置y（t+Tp）与该处的预期轨道坐标f（t+Tp）尽可能相一致。但为了模拟驾驶员分心、疲劳状态而导致车道偏离的情形，假设驾驶员不对前轮转角进行补偿校正。考虑驾驶员反应延迟时间，基于预瞄跟随理论的驾驶员模型框图如图2所示。该模型的输入为前方道路信息（期望路径）与当前车辆状态信息（如车速、偏航角以及车辆的当前位置），输出为驾驶员转向角。

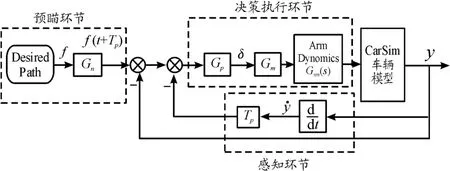
图2 基于预瞄跟随理论的驾驶员模型框图

其中，预瞄迟滞环节为

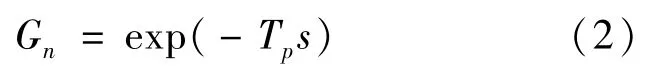
驾驶员输出转向角与预瞄偏差的传递函数关系：

神经反应滞后环节［9］：

手臂反应滞后环节：

式中：A、B、C、D为模型参数；s为拉普拉斯算子；Tp为预瞄时间；δ为驾驶员输出转向角；Td、Th分别为驾驶员神经、手臂反应时间。

1.2 直接横摆力矩控制的车辆动力学模型

虽然14自由度汽车动力学模型，能精确反应汽车真实的运动状态，但是本文的主要目的是对车道保持的车辆进行横向控制，采用仅描述横向动力学的简化模型更加合适。现在广泛使用的2自由度线性单轨模型，可以简单而准确地描述车辆横向动力学，并考虑到车辆转向操作的稳定性，需对车辆施加横向稳定性控制。因此，采用有横摆力矩作用的线性2自由度单轨车辆模型作为参考车辆模型［10］，如图3所示。

图3 单轨车辆动力学模型示意图

在车身坐标系下，根据牛顿第二定律，可以得到车辆横向和横摆运动的受力平衡方程，如下：

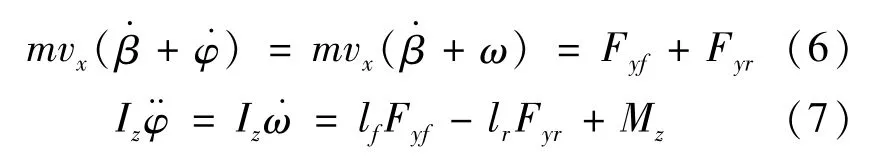
当轮胎侧偏角和滑移率均较小时，可以将轮胎模型视为线性模型，即：

根据小角度假设，可以得到前、后轮胎的侧偏角与车辆运动参数的关系式：

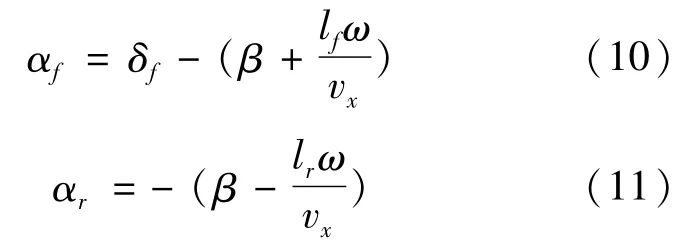
式中：δf是前轮的转向角；Cf、Cr分别为前、后轴等效侧偏刚度；αf为前轮侧偏角；αr为后轮侧偏角。

将式（10）（11）代入式（6）中，得到：

车道保持参考车辆模型中还应包含车辆的速度和车辆的航向角及相对于车道中心线的横向位置［11］，在大地坐标系下：

对式（14）进行线性化，得到：

式中：Y为横向位移；φ为车辆的偏航角。

对于线性2自由度单轨车辆模型，理想的横摆角速度可由下式计算［12］：

2 车道保持辅助系统控制设计

2.1 控制器结构设计

本文所研究的基于人机共驾的车道保持驾驶辅助系统结构如图4所示。该系统由驾驶员和控制系统两部分组成。驾驶员转向角和车辆实际状态与期望状态之差，作为输入量进入模型预测控制器，控制的思想是在车辆行驶过程中使车辆的质心与车道中心线的侧向偏差保持在合理范围内，并对汽车稳定性进行同步控制。经计算得出车辆的矫正转向角和期望横摆力矩。上位控制器计算输出的横摆力矩，又作为输入量进入汽车防侧翻稳定性控制器。该控制器根据期望横摆力矩进行驱／制动分配，并利用差动制动方法计算输出合适的制动压力到CarSim整车模型中。然后通过车辆横向动力学模型计算输出车速、偏航角、横向位移等，如此，构成整个仿真过程的闭环控制系统，实现车辆稳定的跟踪车道线。

驾驶员和控制系统共同操纵汽车时，为避免两者相互干扰，需对车辆控制权限进行分配，即最终的前轮转向角为矫正转向角与驾驶员转向角混合的总和。前轮转向角为：

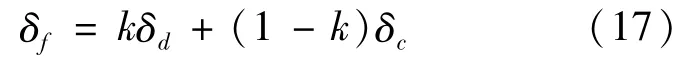
式中：δf为前轮转向角；δd为驾驶员的转向角；δc为控制器施加的矫正转向角；k∈［0 1］为共驾系数。

实际上，人的控制权限是最高的，当出现车道偏离，系统就会干预，但是如果人强制干涉的话，还是以人为主。k＝1时，驾驶员具有完全的车辆控制权；k＝0时，车辆完全由辅助驾驶系统操纵。考虑到当k的值较小时，驾驶员的车辆控制权限低，可能会带给驾驶员不愉快的驾驶经历；当k值较大时，也可能无法达到预期的跟踪效果。因此，本文中采用固定的车辆控制权限分配策略，将其取值为0.5。

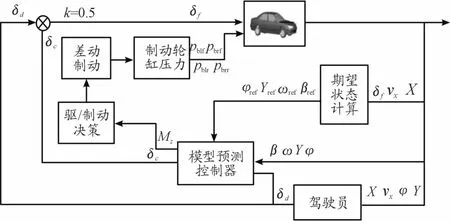
图4 基于人机共驾的车道保持控制器结构框图

2.2 模型预测控制器设计

2.2.1 预测方程

结合式（12）（13）（15）和（17），选取状态变量为x＝［βωYφ］T，控制量为u＝［δcMz］T，得到状态空间方程：

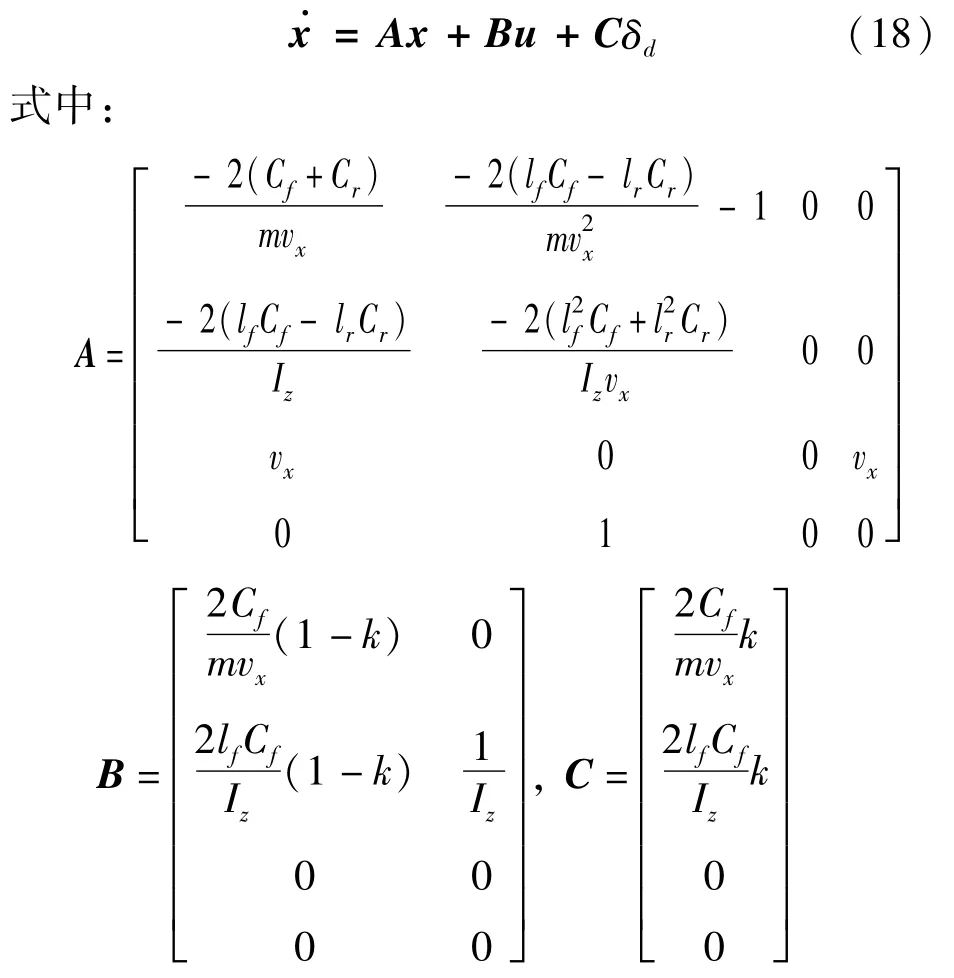
运用1阶差商方法对式（18）进行离散化处理，采样时间为T，得到如下离散状态方程：

在采样时刻k（k＞0），可通过CarSim获得状态变量向量x（k），x（k）提供了当前的车辆信息。根据车辆当前状态信息，通过不断迭代，可以预测未来第k+Np采样时刻的状态变量向量，迭代过程如下：

式中：x（k+i｜k）为在给定当前状态信息x（k）下k+i时刻的预测状态变量向量；Np为预测步长；Nc为控制步长。

从而可以得到如下的预测方程：

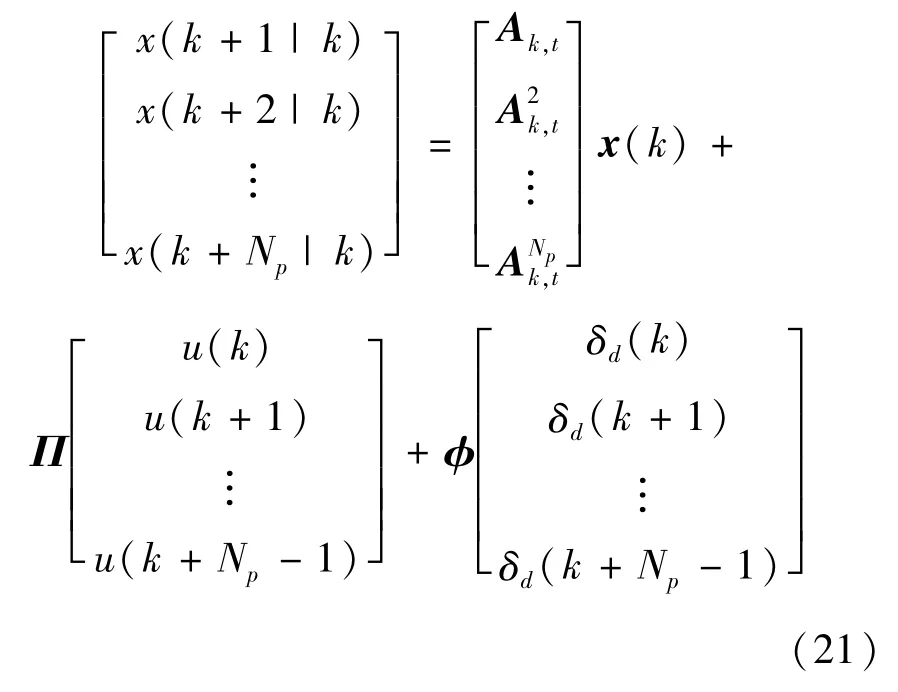
2.2.2 约束条件

考虑到机械结构的饱和限制，前轮的转向角必须保持在转向机构的物理极限之内；此外，为了使转向过程更加平稳，对每个控制周期的矫正转向角增量也施加相应约束，即：

为了保证横向预测控制算法的侧向稳定性，控制算法必须包括避免车辆侧翻的安全约束，即：

结合式（22）和（23），可以得到控制量和控制增量的约束条件：

2.2.3 目标函数

对于目标路径，模型预测控制系统的控制目标是在预测范围Np内，使预测输出尽可能接近参考点，定义控制目标函数为：

第一项为预测的状态向量与期望状态向量差值的平方和，第二项为控制量增量的平方和。参考状态xref＝（βref，ωref，Yref，φref）；Q、R分别为状态量误差权重矩阵和控制量增量权重矩阵，用来描述路径跟踪误差与各控制目标之间的重要程度，因为车道保持的主要目的是使车辆保持车道中心线行驶。本文中主要看重其横向位移，并令它们为固定值，分别为：

理想的横摆角和质心侧偏角为：

2.2.4 二次规划问题

考虑到目标函数为二次函数和约束条件为线性函数，将上述问题转化为如下形式的二次规划命题：

在目标函数中，求解的变量为控制时域内的控制增量，约束条件也只能以控制增量或者是控制增量与转换矩阵相乘的形式出现［12］。因此作如下变换：

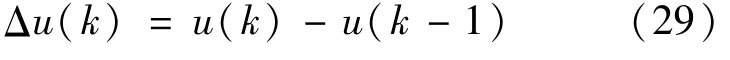
由于模型预测控制采用滚动优化，即在每个控制周期内不断求解最优控制量，所以在每个控制时域内都需要满足约束条件。结合式（24）和（29）得到控制变量在控制时域内的约束表达式为：

将式（30）改写成线性不等式Ax≤b的约束表达形式：

通过Matlab优化函数fmincon中的内点法求解后，得到控制时域内的一系列控制输入增量：

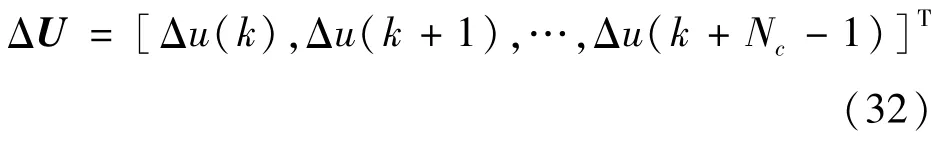
并将控制序列中第一个元素取出来作为实际的控制输入增量，通过式（29）计算得到第k时刻的控制量，然后施加于系统。在下个控制周期，重复上述过程，直至仿真结束。

3 汽车稳定性控制

高速行驶的车辆做曲线运动时容易侧翻，且驾驶员不易察觉，为了提高汽车的横摆稳定性，防止车辆发生侧翻，对车辆进行防侧翻稳定性控制。

目前常采用的方法有单轮差动制动和双轮差动制动。本文采用双轮差动制动方法，即根据汽车的转向特性对两侧车轮进行驱动／制动分配并决策驱动力和制动力值。当车辆处于过度转向时，选择内侧驱动、外侧制动，内外制动力差就会产生向外侧的横摆力矩，降低侧向加速度，避免加重过多转向，提高车辆防侧翻能力；同理，当车辆处于不足转向时，选择外侧驱动、内侧制动，产生向内侧的横摆力矩，避免加重不足转向。以横摆角速度偏差Δω（实际值ωr-期望值ωref）和前轮转角δf方向为指标，判断车辆的转向特性。驱动／制动协调策略如表1所示［13］。

表1 驱动／制动协调策略

对于模型预测控制器计算出的期望横摆力矩，选用平均分配的方式分配给驱动侧和制动侧。则有：

式中：Fμobj为制动侧的总制动力；Fxobj为驱动侧的总驱动力；c为轴距。

因差动制动对车辆纵向速度的影响不大，所以不考虑行驶过程中前后轴的载荷转移，采用固定比值分配制动侧前后轮的制动器制动力，即：

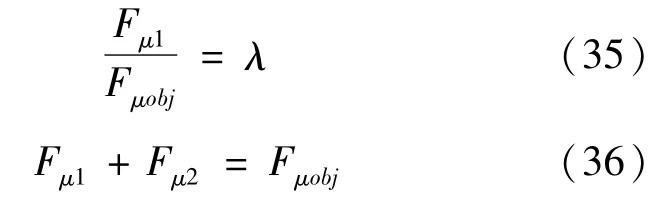
式中：Fμ1为前制动器制动力；Fμ2为后制动器制动力；λ为前、后制动器制动力分配系数。

将制动力转换为轮缸压强：

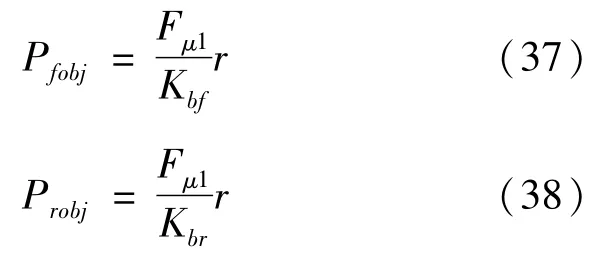
式中：Pfobj为前制动器制动压力；Probj为后制动器制动压力；r为车轮半径；Kbf、Kbr分别为前、后轮的制动效能因数，由制动器作用面积、摩擦因数和制动器半径等决定［14-15］。

4 仿真结果与分析

在CarSim中设置仿真环境，选择CarSim自带的车辆模型C-Class／Hatchback，路面附着系数设置为μ＝0.85，模型预测控制器相关参数如表2所示。在仿真试验中，设置双移线工况和蛇形工况，并分别在低速（36 km／h）和高速（72 km／h）情况下进行试验，输出车辆在辅助驾驶系统干预前后各参数响应曲线。

表2 模型预测控制器相关参数

4.1 双移线工况

为了更加准确地模拟车辆在真实道路的驾驶场景，仿真设置的参考道路必须符合国家公路建设的行业标准，参照标准ISO 3888—2∶2002设置双移线道路，如图5所示。路段1、路段3和路段5为直线道路，而路段2和路段4为曲线道路［12］，为了确保道路曲率光滑、不突变，路段2和4采用5次多项式进行曲线拟合。车道中心线的横向偏移量与道路纵向位移的关系式为：

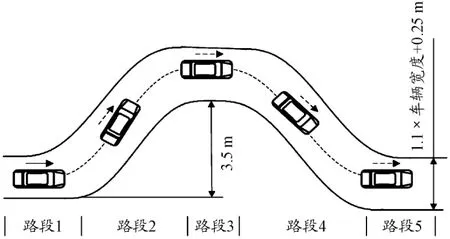
图5 双移线道路仿真场景示意图

图6～8为在双移线工况中，不同车速下有无辅助驾驶系统干预的仿真结果曲线。

图6 双移线工况下2种不同驾驶方式的横向位移

图7 双移线工况下2种不同驾驶方式的横摆角速度偏差

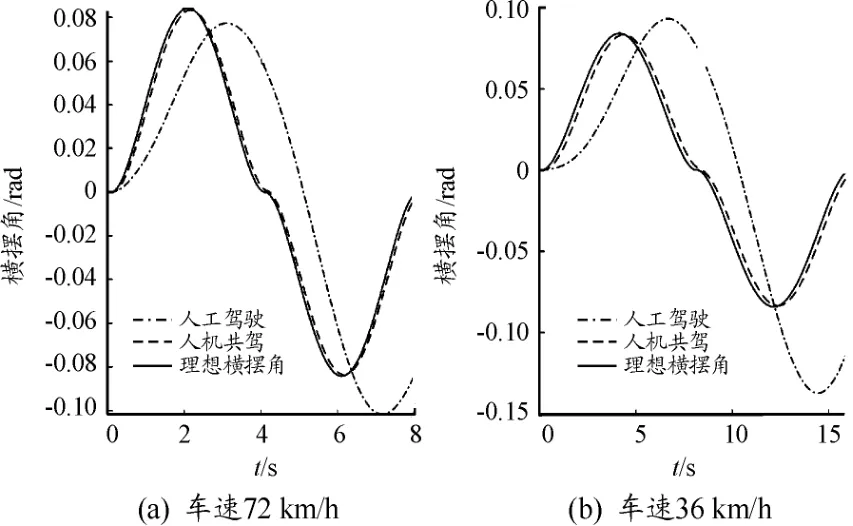
图8 双移线工况下2种不同驾驶方式的横摆角

从图6中可以看出，在全人工驾驶下，车辆横向位置与车道中心线的偏离较大，高速情况在第5 s，低速情况在第10 s时，横向偏移量都超过1 m，此时车辆严重偏离车道线，但LKA开启之后控制器能及时预测车辆将要发生偏离并及时干预驾驶行为，采取转向辅助和稳定性控制。其矫正转角和附加横摆力矩如图9和图10所示。从图中可以看出，驾驶辅助系统能及时抑制车辆的偏离，迅速消除侧向位移偏差，使车辆的横摆角跟随理想值，并使横摆角速度偏差限制在0.008 rad之内，实现了车辆稳定保持车道中心线行驶的效果。综上所述，无论在低速行驶还是高速行驶的情况下，控制器均能及时预测，迅速响应，适应性和鲁棒性强。

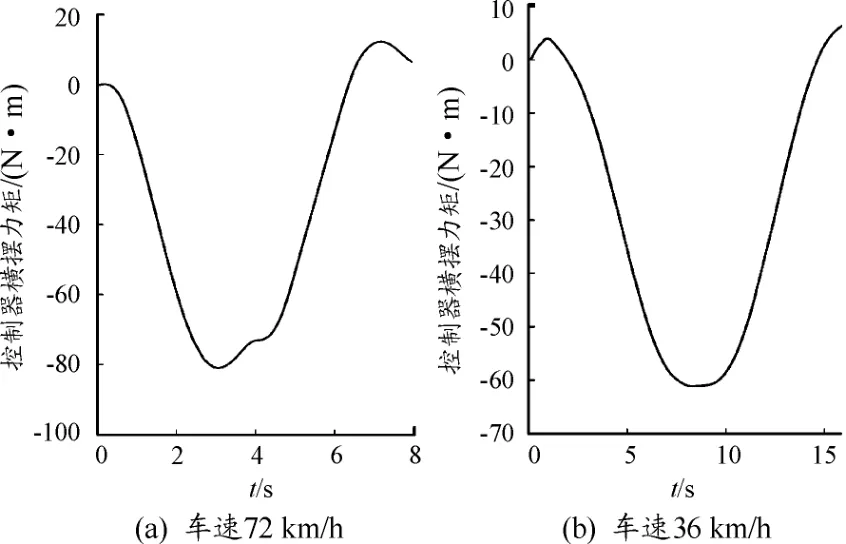
图9 双移线工况下人机共驾方式下控制器横摆力矩

图10 双移线工况下驾驶员转向角和控制器转角

4.2 蛇形工况

为进一步验证控制器的可靠性和鲁棒性，选取湿滑（μ＝0.4）的蛇形路面，进行仿真试验，并基于车辆横向位置信息分析车道保持性能。仿真结果如图11、12所示。从图11中可以看出：在低附着系数路面上，无论是低速还是高速控制器均能及时修正驾驶员操纵下发生车道偏离的车辆，且横摆角速度偏差接近于0，具有较好的可靠性和较强的鲁棒性。

图11 蛇形工况下低路面附着系数的车辆侧向位移

图12 蛇形工况下低路面附着系数的车辆横摆角速度偏差

5 结论

在CarSim中建立了整车模型，利用Matlab／Simulink软件建立了有直接横摆力矩作用的车辆动力学模型、驾驶员模型和模型预测控制器。根据前轮转角、横摆角速度偏差等可测信号提出了汽车防侧翻稳定性控制策略。最后通过Simulink接口，实现了CarSim与Simulink的联合仿真。

选取双移线路面和蛇形路面，在不同车速不同路面附着系数的行驶环境下仿真并验证了人机共驾车道保持驾驶辅助系统的有效性和鲁棒性。仿真试验表明，与全人工驾驶相比，人机共驾的车道保持驾驶辅助系统可有效减小横向偏差，使实际的横向位移与期望的横向位移基本保持一致。采用固定共驾系数的方法可以降低辅助系统与驾驶员的驾驶冲突，提高了车辆的行驶安全性和驾驶舒适性。在低附着系数路面上仍能使车辆高速稳定地保持车道中心线行驶。