超大跨度公铁两用钢箱梁悬索桥设计初探
2021-04-12皮福艳雷俊卿卢文良陈进昌
皮福艳 雷俊卿 卢文良 陈进昌
(1.北京交通大学土木建筑工程学院,北京 100044;2.中铁工程设计咨询集团有限公司,北京 100055)
悬索桥以超大的跨越能力、明确的受力和传力途径及与自然景观相协调的美观外形,成为了超大跨度桥梁设计主要的结构形式之一。我国已经迈入了建设两千米级大跨度桥梁的新时代[1-3]。
悬索桥是以缆索体系承重的柔性结构,而铁路列车运行速度快、自重大且对轨道平顺性要求高,故铁路悬索桥的设计常受到桥梁刚度问题的限制[4-5]。采用公路和铁路合建的形式,既能增加体系的恒载以提高“重力刚度”,又能将公路和铁路同层布置来增加加劲梁宽度以满足体系刚度及抗风要求[6-7]。已建成的主跨1092 m 的五峰山长江大桥是我国第一座大跨度钢桁梁公铁两用的千米级悬索桥[8]。
公铁两用悬索桥是大跨度桥梁的发展趋势。现有桥梁设计规范多适用于大中小跨度桥梁,对于超大跨度公铁两用悬索桥还没有合适的规范可以直接采用,所以千米级超大跨度公铁两用悬索桥的建设还面临许多问题与挑战。
本文拟对主跨为1800 m 的公铁两用悬索桥进行试设计,研究主缆的垂跨比、加劲梁的边中跨比、列车荷载不同的加载长度等对结构体系的受力与变形的影响,分析结构在运营荷载作用下的受力特征,验证设计参数的可行性,为公铁两用悬索桥的理论研究与工程设计提供参考。
1 悬索桥结构初步设计
经过桥梁设计方案比选,最后选择的初步设计的桥型为公铁两用双塔单跨钢箱梁悬索桥[9-14],跨度布置为(72×4+96×2+1800+96×2+72×4)m。采用塔墩固结、塔梁分离、索塔横梁与加劲梁间设竖向支座的半漂浮体系结构。超大跨度悬索桥的结构立面布置见图1。
主缆和吊杆均采用兼具高强度、高扭转与低松弛性能的高强镀锌钢丝,公称抗拉强度为1860 MPa。每侧设置两根主缆,单根主缆直径1.385 m。垂跨比为1/10。单侧主缆下的吊索等效直径为0.07 m,在悬吊长度大于20 m 的吊索中央设置减振架,以减少吊索的风致振动。
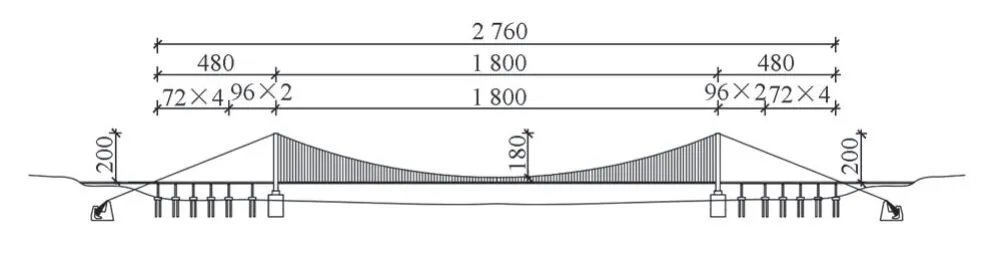
图1 超大跨度悬索桥立面布置(单位:m)
索塔塔底采用沉箱基础,边跨共设6个辅助墩,最大跨度为96 m,桥面与山体间设置引桥。桥塔采用门式框架结构,高为235 m,塔顶至桥面高度为200 m,塔柱与横梁均为空心箱形截面。
加劲梁采用Q420 钢板制作的钢箱梁,总宽度为61.13 m,梁高5.00 m,桥面宽度为54.64 m。顶板厚25 mm,底板厚16 mm,顶底板均设置间距300 mm 厚8 mm 的U 形加劲肋。每隔4 m 布置一道空腹桁架式横隔板,每道横隔板由22根桁架杆组成。为增加桥梁的抗风稳定性,在风嘴外侧增加了挑板以改善气流条件。桥梁横断面布置见图2。
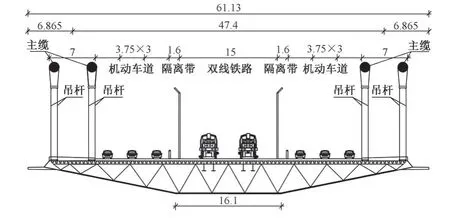
图2 桥梁横断面布置(单位:m)
2 有限元分析
采用通用的有限元分析软件进行数值模拟,有限元模型见图3。主缆和吊索采用非线性空间索单元模拟,加劲梁和索塔采用空间梁单元模拟,共计862个节点、861 个单元。采用主从约束模拟加劲梁与吊索的连接,采用释放顺桥向位移的主从约束模拟塔顶主索鞍,采用弹性连接模拟索塔下横梁与加劲梁之间的支座[15],采用一般支承模拟大地约束。

图3 悬索桥有限元模型
为满足行车平顺性和桥梁安全性的要求,应进行悬索桥在恒载作用下的初始成桥状态分析,以提供最合理的主缆线形与相应的自平衡张力系统。通过对初始成桥状态进行分析计算,得到在自重和桥面铺装等恒载作用下的内力与位移,加劲梁最大竖向位移为0.00137 mm,满足行车平顺性要求。加劲梁最大应力为128.3 MPa,主缆最大应力为424.9 MPa,吊索最大应力为346.8 MPa。
3 设计参数对悬索桥受力性能的影响
3.1 加劲梁的边中跨比
悬索桥的边中跨比是指边孔跨度与主孔跨度的比值,单跨悬索桥的边孔跨度可视为索塔至锚碇散索鞍处的距离,单跨悬索桥的边中跨比一般在0.2 ~0.3之间[16-17]。为研究不同跨度比对悬索桥静力性能的影响,在保持主跨为1800 m、垂跨比为1/10 不变的前提下,改变边孔跨度,分别取350,400,450,515,540,570,600 m,计算悬索桥在恒载与移动荷载共同作用下主要构件的内力与变形,见表1。
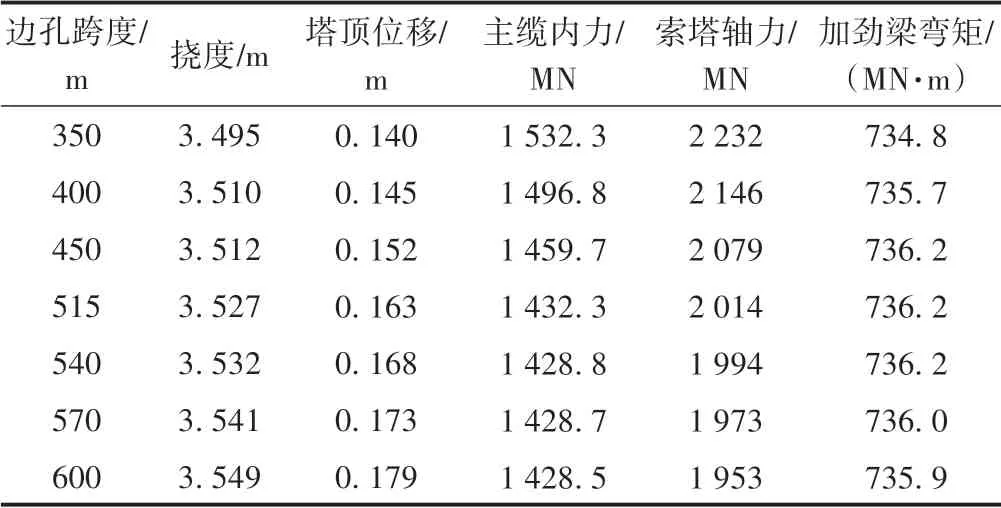
表1 加劲梁的不同边中跨比下悬索桥的内力与变形
由表1 可见:结构变形随着边孔跨度的增大而增大,主缆与索塔的内力随着边孔跨度的增大而减小,加劲梁弯矩受边孔跨度变化的影响较小;边孔跨度从350 m 增大到600 m,跨中挠度与塔顶位移分别增大了1.55%,27.86%,主缆与索塔内力分别减小了6.77%,12.50%。边孔跨度增大的同时用钢量也会增大,故在确定边孔跨度时应兼顾水文与地形条件、结构刚度、经济等多种因素。
3.2 主缆的垂跨比
悬索桥的垂跨比是指主缆在主孔内的垂度和主孔跨度的比值,取值一般在1/11 ~1/10[17]。为研究主缆的不同垂跨比对悬索桥静力性能的影响,拟取主缆的垂跨比分别为1/9.5,1/10.0,1/10.5,1/11.0,计算在恒载和移动荷载作用下桥梁主要构件的内力与变形,计算结果见表2。
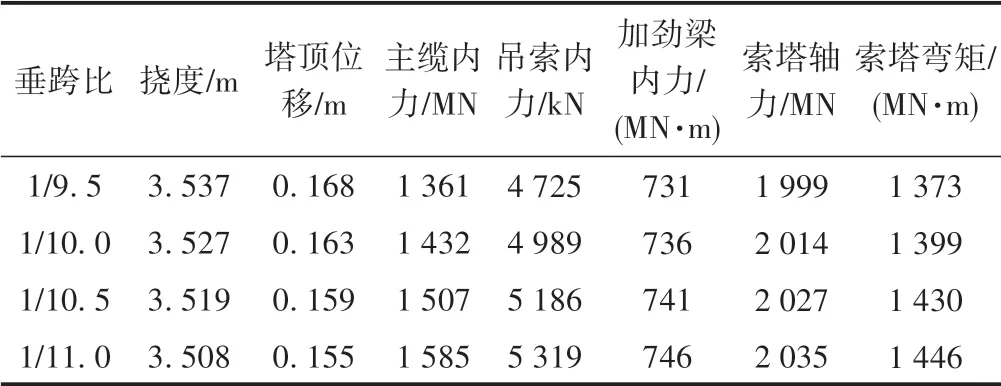
表2 不同垂跨比下悬索桥静力性能比较
由表2可见:结构变形随着垂跨比的减小而减小,主要构件内力均随垂跨比的减小而增大;垂跨比从1/9.5 减小到1/11,跨中挠度和塔顶位移分别减小了0.82%,7.74%,主缆、吊杆和加劲梁内力分别增大了16.46%,12.57%,2.05%,索塔轴力和弯矩分别增大了1.8%,5.32%。主缆和吊杆的内力受垂跨比影响最大,结构刚度随垂跨比的减小而增大。
3.3 不同列车荷载的加载长度
本设计桥梁主跨1800 m 远超过了我国可能开行列车的最大长度,按TB/T 3466—2016《铁路列车荷载图式》中无限长的列车荷载图式[18],全长布满列车荷载的加载形式不符合实际情况。列车长度与桥梁所在线路的到发线有效长度、牵引定数和编组情况有关[19-21]。根据到发线有效长度比选确定了550,750,950 m 三种不同的列车加载长度,对比了不同加载长度下恒载和移动荷载共同作用时悬索桥的内力与变形,见表3。可见,随着加载长度的增大,挠度、加劲梁弯矩与索塔最大轴力增大幅度趋于平缓。
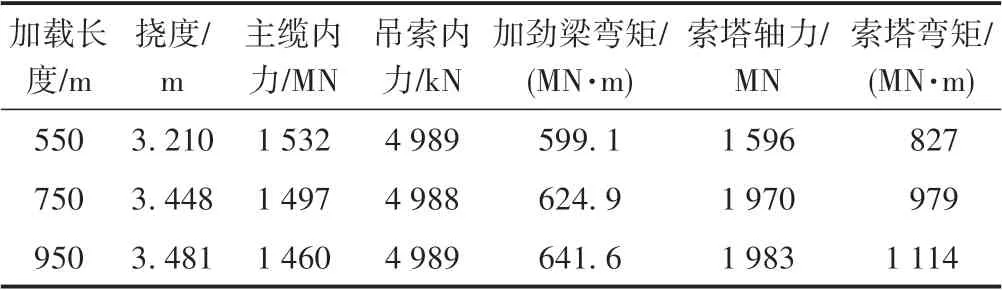
表3 不同列车荷载加载长度下悬索桥的内力与变形
4 不同荷载组合下悬索桥的荷载效应
对悬索桥在自重、二期恒载、ZK 活载、公路I 级活载、整体升降温、桥塔局部温差、风荷载和支座沉降8种荷载下的7种荷载组合进行了计算分析。计算荷载组合见表4。
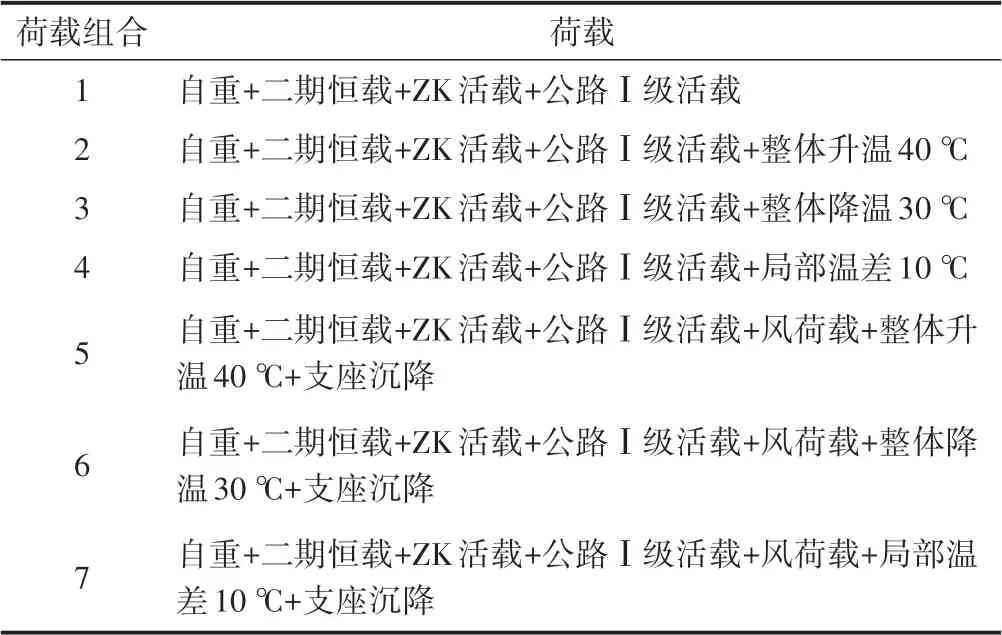
表4 荷载组合
选取桥址处基本风速为25 m/s。考虑我国可能的最大列车开行长度和到发线时间的限制,选择ZK 活载加载长度为950 m。计算活载时,公路荷载考虑横向、纵向折减系数分别为0.55,0.93;公路与铁路组合时,考虑折减系数取0.75。在不同荷载组合下,悬索桥主要构件的应力与位移计算结果见表5。
由表5 可见,在计算的荷载组合下加劲梁最大压应力为156.31 MPa,最大拉应力为142.44 MPa,均满足TB 10002—2017《铁路桥涵设计基本规范》[22]中Q420 钢材容许应力规定。加劲梁跨中最大竖向位移为4.591 m,竖向挠跨比接近1/400,风荷载作用时最大横向位移为1.753 m,横向挠跨比接近1/1000,符合国际上超大跨度悬索桥的变形要求。主缆最大应力为492.21 MPa,安全系数为3.78,吊索最大应力为419.30 MPa,安全系数为4.43,表明安全度具有足够的安全储备。
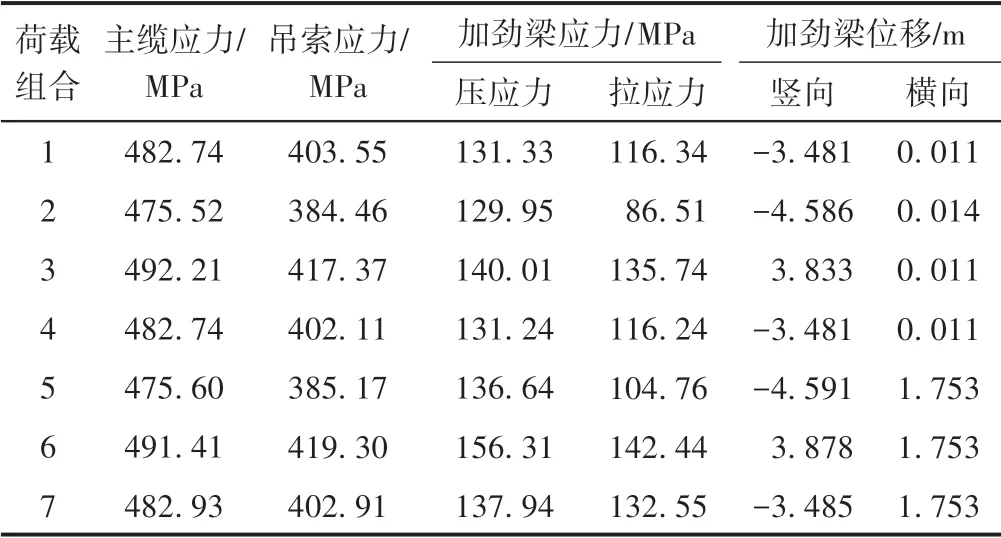
表5 悬索桥主要构件应力与位移计算结果
5 结论
初步设计了一座主跨为1800 m 的公铁两用钢箱梁悬索桥,对加劲梁、主缆、索塔、吊索等主要构件进行了尺寸设计。主要结论如下:
1)探讨了边中跨比、垂跨比对悬索桥静力性能的影响,主缆内力和结构刚度随边中跨比和垂跨比的增大而减小,进行实际桥梁设计时应综合考虑环境限制、经济、可靠性等多方面因素。
2)依据到发线有效长度比选了三种不同的移动荷载加载长度,对悬索桥在主力作用下的静力性能进行了对比分析,结果表明加载长度的不断增大对桥梁主要结构静力性能的影响幅度有所降低。
3)用有限元软件对结构进行数值模拟分析,针对8种不同的设计荷载作用下,计算了7种不同的荷载组合悬索桥的应力与变形:主缆和吊索的最大应力分别为492.21,419.30 MPa,加劲梁最大压、拉应力分别为156.31,142.55 MPa,均符合桥梁设计规范要求,表明了设计的合理性与可行性。
