超大跨度公铁两用悬索桥活载刚度研究
2021-04-12许磊平霍学晋
许磊平 霍学晋
(中铁大桥勘测设计院集团有限公司,武汉 430050)
由于跨江桥位资源宝贵,同时搭载多种交通功能的桥梁更受建设方的青睐,超大跨度公铁两用悬索桥往往是较优方案[1-3]。此类桥梁计算理论复杂,设计难度大,主要表现为:超大跨度桥——属于柔性结构,需采用几何非线性(下文简称非线性)分析理论计算;公铁两用桥——同时搭载公路、铁路,设计活载往往比单一功能桥梁大很多。结构方案比选的重要指标是活载刚度,且活载效应受各构件共同影响。当跨度超过千米后,需对影响结构活载刚度的各项因素进行参数研究。
国外学者对非线性理论研究较早,多采用挠度理论。Wollmann[4]基于挠度理论建立了一种用于求解非线性效应的实用解法;Clemente 等[5]利用挠度理论分析了大跨度悬索桥设计参数对结构力学性能的影响,发现随着跨度的增加,悬索桥受力特性逐渐趋近单根主缆的力学特性;Jennings[6]忽略活载对主缆内力的影响,对集中荷载及均布荷载作用下公铁两用悬索桥主缆变形特征进行了研究,发现活载较大时,若直接忽略活载对成桥内力的影响会存在一定的偏差。国内学者在此基础上,将非线性理论应用到悬索桥上,并对其特有的问题开展了一系列研究。沈锐利等[7]对悬索桥开展了静动力空间非线性计算有限元模型的研究工作,并应用到实际工程中;唐茂林等[8]提出了悬索桥成桥主缆线形计算的分段悬链线法,求解精度大大提高;柴生波等[9]研究了悬索桥桥塔顶位移、主缆的弹性伸长及不平衡均布活载作用下的主缆变形特性。
为了提高列车通过铁路桥梁时的行车安全性及舒适性,桥梁刚度需满足一定的要求。TB 10002—2017《铁路桥涵设计规范》[10]对铁路桥梁刚度提出了限制性要求,主要对梁体的挠跨比、横向变形、梁端转角等指标进行了限制。然而该规范仅适用于跨度不大于168 m 的钢梁、跨度不大于128 m 的混凝土梁和墩高不大于50 m的桥梁。
本文以实际工程为背景,采用中铁大桥院自主研发的大跨度悬索桥非线性计算分析软件SNAS 开展研究工作,建立基于全量法的非线性和混凝土收缩徐变的耦合算法,采用完全非线性算法求解活载。基于超大跨度公铁两用悬索桥成桥线形,以找形结果为基础,建立悬索桥精细化有限元模型,对活载作用下悬索桥的非线性效应、矢跨比、主塔刚度、边缆跨度、边跨加劲梁梁长等进行详细分析,研究不同参数对悬索桥活载刚度的影响规律。
1 工程概况
一座跨越长江的公铁两用悬索桥,桥址区主通航孔较宽。为不影响通航,采用超大主跨悬索桥跨越主通航孔。综合比选设计中满足通航需求的多个结构方案,选取主跨1560 m 超大跨度悬索桥方案进行研究,孔跨布置为(2×120+1560+2×120)m,如图1所示。

图1 结构方案(单位:m)
为节约桥位资源,该桥同时搭载高速公路、高速铁路和客货共线铁路。加劲梁采用钢桁梁断面(图2),上下双层布置。上层桥面为双向八车道高速公路,设计速度100 km/h。下层桥面上游侧为双线高速铁路,设计速度350 km/h,到发线有效长度650 m;下游侧为双线普通铁路,设计速度160 km/h。
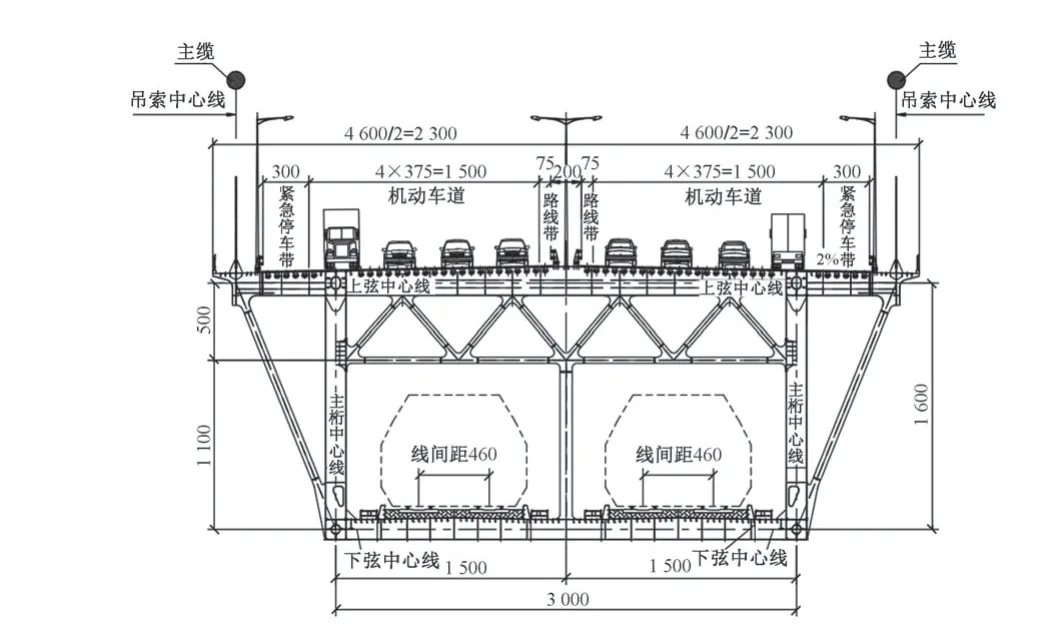
图2 主梁横断面(单位:cm)
2 成桥状态确定
悬索桥成桥状态的计算是开展运营阶段分析的基础。悬索桥的成桥线形是指在结构恒载(一期恒载与二期恒载)作用下,悬索桥逐阶段施工至竣工时刻在设计基准温度下的结构线形。本文基于精确悬链线理论确定成桥状态下主缆和吊杆的无应力长度,更新悬索桥有限元模型并开展参数敏感性分析。
在SNAS 中建立全桥空间有限元模型。主缆和吊杆采用空间索单元模拟,主塔和加劲梁采用空间梁单元模拟;主塔底固结,主缆在锚碇位置固结,采用主从连接模拟支座以及缆塔间的连接。

图3 成桥状态
成桥状态见图3。可知,中跨加劲梁最大变形为3.6 cm,线形较好;有索区钢梁最大应力31.4 MPa,应力较低;主缆和吊杆的轴力分布均匀,可作为进一步分析的基准状态。
3 活载刚度研究
上层桥面高速公路采用公路一级荷载,按照车道数和跨度进行横向多车道折减和纵向折减;下层桥面双线高速铁路选取ZK 活载;双线普通铁路采用中-活载。根据到发线长度650 m 并考虑安全距离,ZK 活载和中-活载分别采用550,970 m 定长加载。重点研究悬索桥的挠跨比、梁端转角及梁端纵向位移3 个总体刚度指标。
3.1 活载非线性影响
对于超大跨度公铁两用悬索桥,活载产生的结构内力和变形是重点设计内容。为了节约计算时间,悬索桥活载效应通常采用线性理论计算。随着悬索桥跨度的增大,活载的非线性效应愈发显著。非线性对活载效应的影响程度应通过数值分析确定。为此,对主跨1560 m 悬索桥分别采用线性及非线性2 种方法分析其活载效应,刚度指标见表1。以线性分析结果为基数1,将非线性分析结果与其作商,见图4。

表1 线性和非线性分析刚度指标
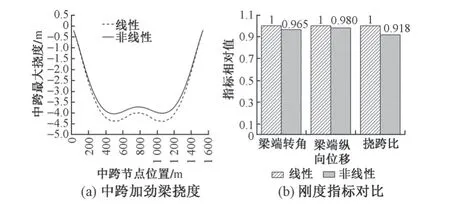
图4 线性和非线性分析结果对比
由表1 和图4 可知:①超大跨度悬索桥在活载作用下的变形呈W 形,2 种分析方法得到的2 个极值点均出现在约L/4 和3L/4 处(L为主跨跨度)。②线性分析方法及非线性分析方法得到的活载挠度最大值分别为4.402,4.040 m。由于非线性分析方法精确,可认为采用线性方法分析该桥的活载挠度比实际值偏大8.96%。③梁端转角对行车性能影响较大,采用2种分析方法得到的梁端转角相差较小,梁端纵向位移接近。
综上,采用线性方法分析桥梁活载、加劲梁挠度、梁端转角及梁端纵向位移均被高估,从经济性方面考虑,建议采用非线性方法。
3.2 矢跨比影响
矢跨比对结构的受力性能具有重要的影响。因此,分析矢跨比分别为1/9,1/10,1/11 时悬索桥的受力规律。矢跨比敏感性分析结果见表2。以矢跨比为1/10 时的分析结果作为基数1,将不同矢跨比的分析结果与其作商进行矢跨比影响分析,见图5。
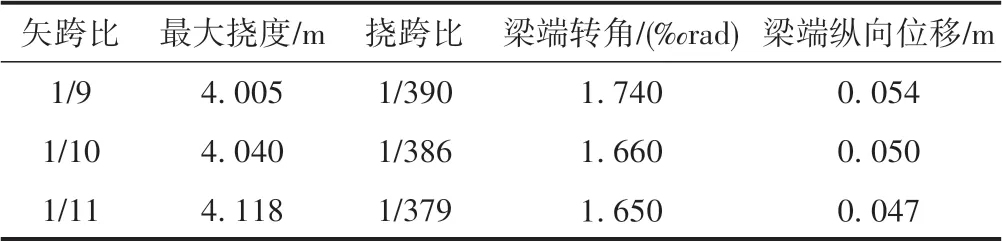
表2 矢跨比敏感性分析结果
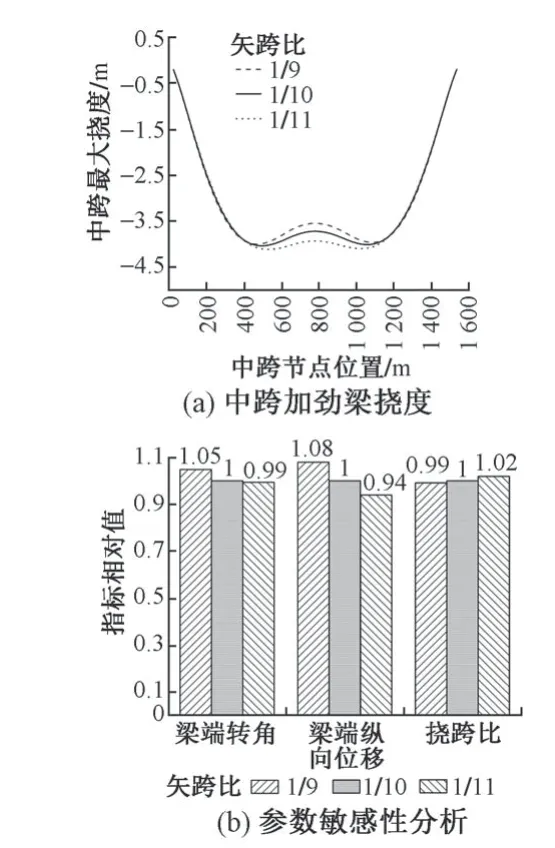
图5 矢跨比影响分析
由表2 和图5 可知,①随着矢跨比的减小,梁端转角逐渐减小,说明增加主跨跨度改善了桥梁的行车性能。②梁端纵向位移逐渐减小。对大跨度桥梁而言,温度和活载引起的梁端纵向位移大,设置梁端伸缩装置困难,且大位移量的伸缩装置是铁路桥梁构造的薄弱点。因此,减小矢跨比可以降低梁端伸缩装置的设置难度。③主跨挠跨比逐渐增加,说明结构刚度降低。因此,适当提高矢跨比可降低跨中挠度。目前,规范仅针对小跨度桥梁的挠跨比有规定,对超大跨度悬索桥尚无明确规定。
3.3 主塔刚度影响
悬索桥属缆索体系桥梁,结构的刚度由主缆、吊索、主塔、加劲梁等构件共同提供。超大跨度悬索桥的主塔较高,主塔截面的选取需要同时考虑强度和刚度要求。以主塔设计刚度为基数1,通过调整主塔刚度倍数(表3)来分析主塔刚度对结构总体刚度的影响,见图6。
由表3 和图6 可知:①随着主塔刚度的提高,梁端转角变化十分微小,说明提高主塔刚度对边跨加劲梁端转角的改善作用极小;②梁端纵向位移从0.050 m逐渐降低到0.038 m,说明提高主塔刚度可有效降低梁端伸缩量;③主跨挠跨比从1/386 降低到1/399,结构刚度略有改善,但效果不明显。

表3 主塔刚度敏感性分析结果

图6 主塔刚度影响分析
本文分析主塔刚度对悬索桥总体刚度的影响时没有考虑鞍座抗滑问题,设计中应综合考虑主塔刚度对结构总体刚度及鞍座抗滑的影响并进行优化。
3.4 边跨主缆跨度影响
边跨主缆为中跨提供锚固作用,锚固作用的强弱与边跨主缆跨度(边跨主缆沿水平投影长度)有一定的关系。因此,分析边跨主缆跨度分别为350,550,750 m 时结构的刚度变化规律,边跨主缆跨度敏感性分析结果见表4。以边缆550 m 跨度的分析结果作为基数1,将不同边跨主缆跨度的分析结果与其作商进行矢跨比影响分析,见图7。

表4 边跨主缆跨度敏感性分析结果
由表4 和图7 可知:①随着边跨主缆跨度的增加,梁端转角略有增加,说明提高边跨主缆跨度对梁端转角的改善作用不明显;②梁端纵向位移从0.048 m 逐渐增加到0.053 m,说明边跨主缆跨度的增加不利于梁端伸缩装置的设置;③主跨挠跨比从1/400 增大到1/364,说明边跨跨度越大,边跨主缆的锚固作用越弱,因而跨中挠度增加。
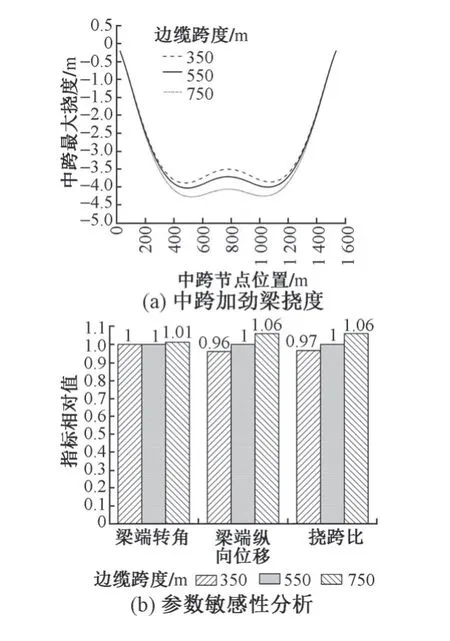
图7 边跨主缆跨度影响分析
3.5 边跨加劲梁长度影响
分析边跨加劲梁长度分别为2×60 m,2×120 m,2×180 m 时结构刚度的变化规律,其敏感性分析结果见表5。以边跨加劲梁长度为2 × 120 m 时的分析结果作为基数1,将不同边跨加劲梁长度的分析结果与其作商进行边跨加劲梁长度影响分析,见图8。

表5 边跨加劲梁长度敏感性分析结果
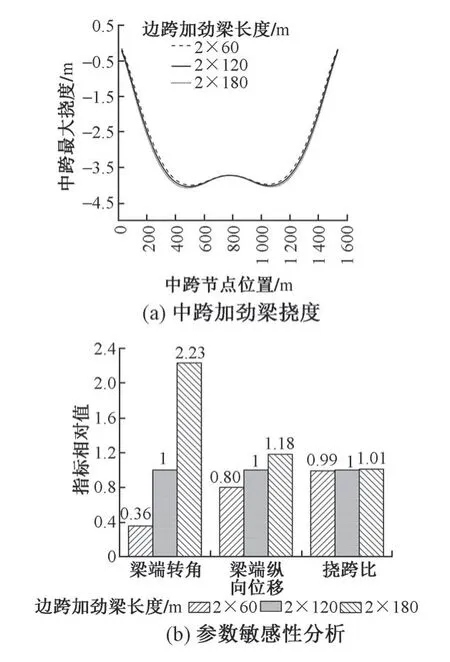
图8 边跨加劲梁长度影响分析
由表5 和图8 可知:①随着边跨加劲梁长度的增加,梁端转角显著增加,这是因为边跨梁端转角受结构自重影响较大,且受跨度影响十分明显;②梁端纵向位移从0.040 m逐渐增加到0.059 m,增加了梁端伸缩装置的设置难度;③主跨挠跨比从1/390 增大到1/383,说明结构刚度有所降低,但变化较小。
4 结论
1)超大跨度公铁两用悬索桥采用悬链线理论确定其成桥线形具有较高的精度,满足精度要求。
2)基于线性方法得到的活载效应比非线性方法的数值偏大。从设计方面和经济性考虑,超大跨度悬索桥应选取非线性方法分析活载效应。
3)公铁两用悬索桥在活载作用下的变形受多个参数的影响。适当减小矢跨比,可降低梁端纵向变形及梁端转角;提高主塔刚度可显著降低梁端纵向变形;减小边跨主缆跨度可增强其锚固作用,提高结构刚度;不同的边跨加劲梁长度对梁端转角及梁端纵向变形具有较大影响,而对挠跨比影响小。
