大跨度连续梁桥弹塑性动力响应分析
2021-04-12吴芮郑史雄贾宏宇杨健陈应高赵灿晖
吴芮 郑史雄 贾宏宇 杨健 陈应高 赵灿晖
(1.西南交通大学土木工程学院,成都 610031;2.贵州省交通规划勘察设计研究院股份有限公司,贵阳 550081)
我国地处太平洋板块和亚欧板块交界处,地震活动频繁且能量巨大,地震灾害对桥梁工程影响极大。结构在罕遇地震作用下会进入塑性变形阶段,大跨度桥梁的非线性特征明显,而弹性计算不能反映结构的非线性特性。依据桥梁结构真实受力行为进行动力分析是实现桥梁合理抗震设计的前提和关键,因此,人们开始研究非线性动力分析方法[1]。20世纪60年代,Newmark 等[2]首先提出“延性”的概念以表明结构物超过弹性阶段的抗震能力,延性大小是结构物抗震能力强弱的重要标志。抗震思想开始从基于强度设计转向基于性能设计。基于位移的抗震设计是实现基于性能抗震设计思想的一条有效途径,20世纪90年代初,Moehle 等[3-4]提出了基于位移的抗震设计理论。但这种方法对由强度控制的脆性结构或延性结构中的脆性构件是不适用的。目前,各国规范中主要采用的抗震设计方法是由Park,Paulay 等[5-6]提出的能力设计原理。该方法指出对于结构的非弹性响应设计,首先布置可能出现塑性铰的位置,使结构屈服后形成一个合理的耗能机构,保证被保护构件在结构塑性铰形成后仍保持弹性,确保结构不会发生脆性破坏。为模拟桥梁构件进入塑性状态后的变形,弹塑性动力时程成为国内学者们采用的主要分析方法,以了解结构因地震动破坏的机理,提高桥梁抗震能力[7]。
基于上述研究,本文以一座大跨度连续梁桥为研究背景,采用SAP2000 软件建立有限元数值模型,并在桥墩底部定义塑性铰以模拟地震作用下的塑性变形行为,并进行非线性动力时程分析,研究弹塑性动力响应差异。
1 弹塑性理论
1.1 振动方程及求解
一个非弹性体系可采用数值求解的运动方程表示,即
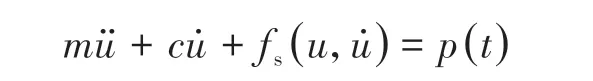
或

式中:m为质量;为加速度;c为阻尼系数;为速度;fs(u,)为非弹性体系的抗力;p(t)为作用力;t为时间;g(t)为地面加速度。
初始条件为

式中:u0为初始位移;0为初始速度。
假定体系具有线性黏滞阻尼,且p(t)由一系列离散值给出:pi=p(ti),i= 0,1,2,…,N;时间间隔Δti=ti+1-ti,且为常数。在离散时刻ti确定反应,单自由度体系的位移、速度和加速度分别为ui,和。假定这些值已知,ti时刻满足式(1),则有

式中:(fs)i是ti时刻的抗力,对于线弹性体系,(fs)i=kui,k为体系的侧向刚度;对于非弹性体系,(fs)i依赖ti时刻以前的位移时程和速度。
选择合适的数值分析方法能够确定ti+1时刻满足式(1)的响应ui+1,+1和+1,即

连续使用时间步进法可给出i=0,1,2,…,N所有瞬时所需反应。已知的初始条件u0=u(0)和0=(0)提供了起动该方法的必要信息[8]。
1959年,N.M.Newmark 发展了一类时间步进法,公式[9]为

式中:γ为初始和最终加速度对速度改变贡献的权重系数;β为初始和最终加速度对位移改变贡献的权重系数。
参数γ和β定义了时间步内加速度的变化水平,决定了方法的稳定性和精度特征。Newmark法精度非常高,是地震反应分析中最流行的方法。
1.2 塑性铰模拟
在SAP2000 中通过离散铰来考虑结构的非线性行为,每个铰属性具有对6 个自由度中任意数目指定的塑性属性。轴力和2个方向的弯矩可通过一个相关作用面来耦合,本文使用的是基于在铰位置轴力和弯矩相互作用的PM2M3耦合铰。对于PMM 铰,在三维PM2M3空间指定一个相关(屈服)面,代表对轴力P、次弯矩M2和主弯矩M3的不同组合最先发生屈服的位置。SAP2000 中的塑性铰用一个离散点模拟,所有塑性变形都发生在点铰内,因此须先假定铰长度,在此基础上对塑性应变或塑性曲率积分[10]。
1.2.1 塑性铰位置的确定
延性抗震设计首先要确定结构易于出现塑性铰的位置[11]。强震作用下,桥墩最大弯矩发生在墩底,高墩墩底的破坏形式更接近弯曲破坏,桥墩底部会发生明显的塑性变形,根据JTG/T B02-01—2008《公路桥梁抗震设计细则》[12]第6.2.2 条规定:沿顺桥向,连续梁桥、简支梁桥墩柱的底部区域为塑性铰区域。为模拟桥墩底部发生的转动,在桥墩底部设置塑性铰。将已定义的塑性铰指定给桥墩底部的单元,模拟其塑性变形行为。
1.2.2 塑性铰的力-位移曲线
对每个自由度定义一个屈服值和塑性变形的力-位移曲线,如图1所示。在a点和b点之间铰内没有变形发生,即铰屈服前被假定为是刚性的。IO,LS和CP点代表铰的能力水平,分别对应直接使用、生命安全和防止倒塌[10]。

图1 塑性铰的力-位移曲线
2 工程背景
一座大跨度连续梁桥位于中国西部贵州省仁怀至赤水高速公路段上,由(88.9 + 168.0 + 88.9)m 预应力混凝土连续箱梁组成(图2)[13]。桥址属于Ⅱ类场地,主梁为混凝土箱梁,截面形式为单箱单室,主梁和桥墩截面见图3。

图2 桥梁立面(单位:cm)

图3 主梁和桥墩截面(单位:cm)
3 数值模型及计算分析
3.1 空间有限元模型
为研究大跨度连续梁桥梁弹塑性动力响应,采用SAP2000 进行建模,桥梁非线性动力学分析模型如图4所示。
主梁单元有95 个节点,选用C55 混凝土,桥墩单元有30 个节点,选用C40 混凝土,钢筋选用HRB335。无约束混凝土滞回模型采用Mander混凝土本构模型,钢筋采用双折线模型。1#,2#墩均采用支座支承力为6 MN 的GPZ(Ⅱ)盆式橡胶支座,容许位移为3 mm。材料本构模型及支座单元模型见图5。

图4 有限元模型

图5 材料本构模型及支座单元模型
盆式橡胶支座的竖向刚度根据支座承受的最大反力和容许位移来计算。为求解盆式橡胶支座的初始刚度,须要得到支座承受的最大反力。先在桥墩顶部和0 号块之间建立刚臂,从左到右分别为刚臂1#和刚臂2#,然后得到在自重荷载下的刚臂内力,并作为支座反力代入计算盆式橡胶支座的刚度公式。经计算得到刚臂1#和刚臂2#的初始刚度k1和k2分别为6.9040×105,6.9046×105kN/m-1。桥梁两侧边跨端部均约束z,y方向的平动自由度。
3.2 计算分析
3.2.1 模态分析
采用多重Ritz 法对该桥进行模态分析,前10 阶模态振动频率f自振和振型如表1 所示。可知,该桥前10阶基本振型主要为主梁的竖向和横桥向振动。查看模态分析结果,该桥第1 阶顺桥向振型参与系数为69.29%,说明其动力响应受高阶振型影响较小。
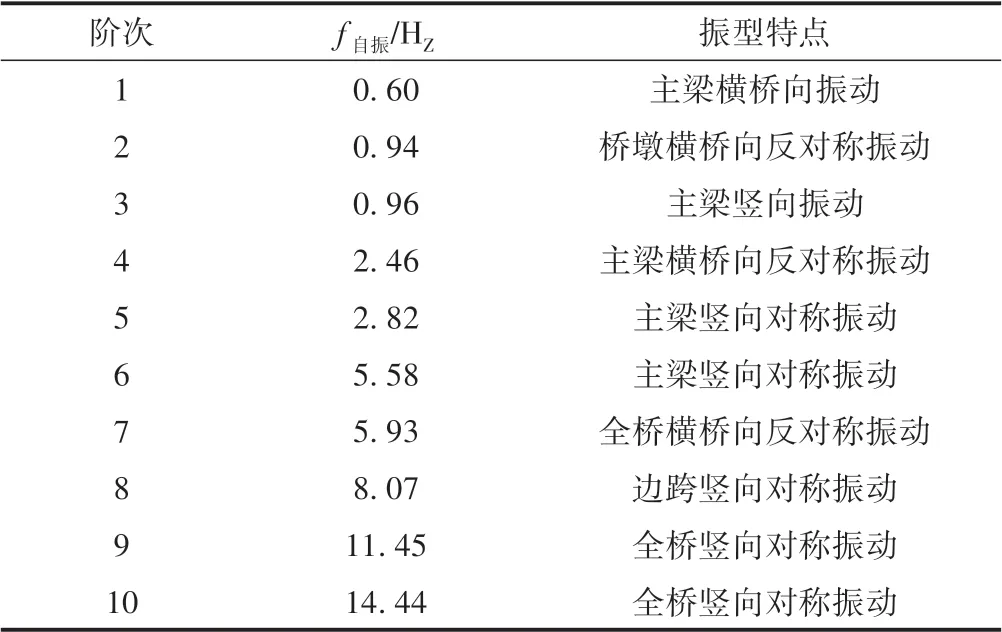
表1 动力特性
3.2.2 地震波输入
选取3 条人工合成地震波,超越概率为4%,峰值加速度为4.524 m/s2,属于罕遇地震烈度下地震波。地震波函数共有2048 个点,步长0.02 s。3 条地震波样本如图6所示。
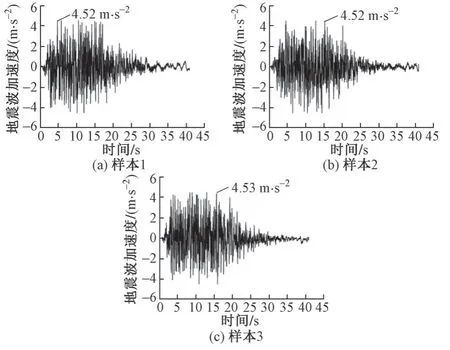
图6 地震波样本
3.2.3 弹塑性分析
1)工况设置。为研究顺桥向和横桥向地震波作用下的动力响应,拟取2种工况:工况1,顺桥向地震激励;工况2,顺桥向激励+横桥向激励。每个地震样本都要考虑2 种工况,并分别进行弹塑性时程分析。JTG/T B02-01—2008第6.5.2条规定,采用3组时程地震波进行计算,响应结果取3组计算结果的最大值。

表2 弹性分析墩底受力情况
2)内力对比。为研究大跨度连续梁桥梁的弹塑性动力响应规律,探究塑性铰在地震下的耗能作用,分析2 种工况下墩底受力情况,分别见表2 和表3。可知:①采用弹性分析方法时,工况2 比工况1 的横桥向弯矩显著增加,说明对桥梁施加横桥向地震作用会明显增大横桥向内力响应;采用塑性分析方法时,工况2比工况1 的顺桥向弯矩有小幅度减小,最大减幅为10.94%,说明塑性分析方法中同时施加2 个方向的地震波对桥墩顺桥向弯矩有削弱作用。②采用塑性分析方法时,桥墩顺桥向及横桥向弯矩均比弹性分析时有所减小,最大减幅为51.21%,最小减幅为26.10%,说明塑性分析方法中桥墩的塑性变形吸收和消耗了部分地震波能量使桥墩内力减小。③无论采用弹性分析方法还是采用塑性分析方法,地震作用对桥墩轴力不会产生影响。

表3 塑性分析墩底受力情况
3)位移对比。各工况作用下桥墩位移时程曲线见图7。可知:①采用塑性分析方法时桥墩墩顶位移比弹性分析方法时明显增大,最大增幅出现在工况2中1#墩墩顶横桥向位移,为325.00%,最小增幅为工况1 中1#墩墩顶顺桥向位移,仅25.14%。②采用塑性分析方法时桥墩墩顶转角比弹性分析方法时增加显著,最大增幅出现在工况1 中1#墩墩顶顺桥向转角,为681.82%,最小增幅为工况2 中1#墩墩顶横桥向转角,为105.88%。说明采用塑性分析方法时桥墩由于允许塑性变形而使墩顶位移和转角均增大,且转角增加更明显。

图7 各工况作用下桥墩位移和转角时程曲线
4)塑性铰分析。分析截面弯矩曲率曲线可知,墩底截面的弹性极限曲率为2.69×10-4rad/m,破坏极限曲率为1.16 × 10-2rad/m。采用塑性分析方法得到塑性铰产生的最大曲率,与墩底截面弯矩曲率曲线分析得到的弹性极限曲率和承载力极限曲率进行对比来判断塑性铰的能力水平。塑性铰响应见图8。可知,工况1中1#墩塑性铰M3方向曲率最大值为1×10-4rad/m,小于墩底截面的弹性极限曲率,仍处于弹性范围。工况2 中1#墩塑性铰M3和M2方向曲率最大值分别为5.20×10-4,1.07×10-3rad/m,均大于墩底截面的弹性极限但小于破坏极限,说明工况2 中1#墩塑性铰已进入塑性发展阶段。由于本文桥梁为对称结构,2#墩塑性铰发展情况与1#墩相同,所有塑性铰曲率最大值均未超过墩底截面的破坏极限曲率,即所有塑性铰没有达到承载力破坏极限。
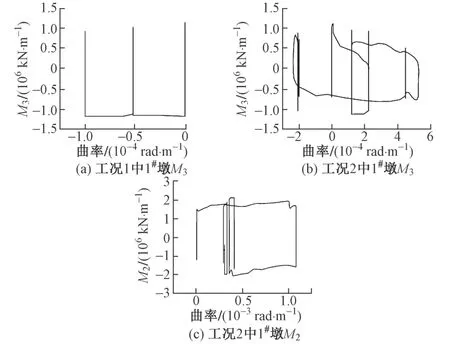
图8 塑性铰响应
4 结论
1)塑性分析中桥墩发生的塑性变形吸收和消耗了部分地震波能量,增加了墩顶的位移和转角,提高了构件的延性,使桥墩的内力减小。
2)塑性分析中同时施加2个方向的地震波对桥墩顺桥向弯矩有削弱作用;地震作用对连续梁桥桥墩的轴力不会产生影响。
3)通过塑性铰能力分析可知,2 座桥墩的塑性铰均已进入了塑性发展状态,但未超过其承载能力极限状态,处于安全使用范围内。
