黏滞阻尼作用下高墩大跨度连续刚构-拱组合桥减震效果分析

王晓鹏

（兰州铁道设计院有限公司，兰州 730000）

大跨度连续刚构-拱组合桥是目前结构比较新颖、发展空间很大的一种桥梁。连续刚构-拱组合桥主要由梁承担梁体自重，由梁、拱共同承担二期恒载和活载，荷载在梁、拱中产生的内力大部分转变为形成自平衡体系的相互作用力［1-2］。与常规梁拱组合桥相比，虽然该类桥的拱与梁在受力方面的优点得以充分发挥，大大削减了结构弯矩和剪力的峰值，但其仍保留连续刚构桥刚度大的特点，墩顶与梁底固结处、墩底在地震荷载作用下均会形成塑性铰，对墩身的损伤较大［3］。因此，连续刚构-拱组合桥的抗震成为该类桥亟待解决的问题。

传统抗震方法是依靠构件的弹塑性变形来吸收地震能量。该方法在一般情况下有效，但仍存在一些问题，如采用该方法须构件截面比较大，会浪费材料。而通过在结构某些部位设置黏滞阻尼器，可依靠该装置产生的摩擦、弯曲以及弹塑性滞回变形来消散或吸收地震产生的能量，从而达到减震目的［4］。黏滞阻尼器是目前最常用的消能减震装置，在各类结构中均表现出显著的减震效果。文献［5］探讨了液体黏滞阻尼器应用于超高层建筑中的相关问题。文献［6-7］研究了液体黏滞阻尼器的阻尼系数对高速铁路连续梁桥动力特性的影响。文献［7］研究了黏滞阻尼器参数、安装位置对自锚式悬索桥减震效果的影响。文献［8］通过在连续刚构桥边墩墩顶设置黏滞阻尼器，分析黏滞阻尼器参数与墩底地震响应、墩梁相对位移的关系，探讨黏滞阻尼器对结构抗震性能的影响。总的来说，目前黏滞阻尼器在高墩大跨度桥梁的运用较为广泛，但对连续刚构-拱组合桥的减震效果研究较少。

基于此，本文以西（安）—延（安）高速铁路连续刚构-拱组合桥为工程背景，利用数值模拟方法分析在该桥两边墩墩顶设置液体黏滞阻尼器后地震作用下墩底内力及主梁位移的变化情况，继而通过改变阻尼参数分析桥墩内力随参数的变化情况，确定该组合桥减震效果最佳时的阻尼参数。

1 工程概况

西延高速铁路连续刚构-拱组合桥位于王家河河段，王家河两岸城市道路交错，另有王家河矿山专用铁路顺河而过。主桥采用（124+248+124）m 连续刚构-拱组合形式，全长497.5 m。主梁采用变截面单箱双室截面，C60混凝土。两侧腹板为直腹板，箱梁顶宽14 m，底宽10.6 m。拱肋呈二次抛物线形，矢高49.6 m，矢跨比1/5。全桥设44 组双吊杆，顺桥向间距9 m，共88根。全桥立面如图1所示。

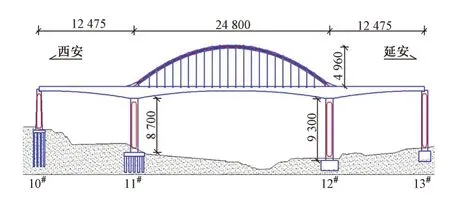
图1 西延高速铁路连续刚构-拱组合桥立面（单位：cm）

2 数值模拟

2.1 模型的建立

本桥为大跨度连续刚构-拱组合桥，由于主墩与梁体固结，在地震作用下边墩处墩和梁的相对位移较大，故将液体黏滞阻尼器设置在两边墩与主梁之间，主梁左右两侧沿横向各设置4个，共8个。

液体黏滞阻尼器由缸体、活塞和流体组成，缸内为硅油或者其他黏滞流体，活塞带有适量小孔，在缸体内部做往返运动［9］。采用液体黏滞阻尼器对桥梁结构进行减震设计时，因为液体黏滞阻尼器表现出较强的依赖频率的性质，所以一般采用Maxwell 力学模型来模拟，如图2 所示。其中：f为液体黏滞阻尼器单元内力；C为阻尼系数；dd，db分别为黏滞阻尼器、弹簧的变形；kb为弹簧刚度；N1，N2为单元节点编号。

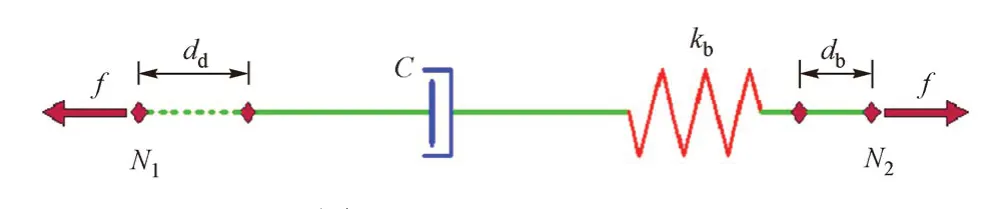
图2 Maxwell力学模型

在该力学模型中弹簧单元一般取一个较大的值，阻尼力F取决于活塞运动速度V。其计算公式为

式中：C为阻尼系数；α为速度指数。

由式（1）可知，C和α的取值对结构减震效果有较大的影响。

运用MIDAS/Civil有限元分析软件，建立结构动力特性和地震反应分析的全桥有限元模型，三维空间有限元模型（图3）阻尼器采用Maxwell 力学模型建立，全桥各部件均采用空间梁单元模拟，吊杆采用桁架单元模拟。拱轴线为抛物线，拱上节点位置根据拱轴线方程计算得出。钢筋、混凝土等材料的参数根据设计确定。

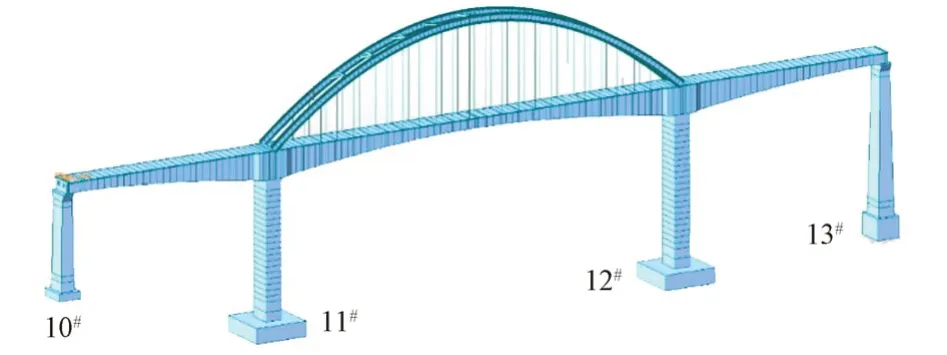
图3 全桥有限元模型

2.2 地震波选取

由于该桥结构的特殊性，对桥址区作了专门的地震安全性评价。采用拟合基岩反应谱的三角级数迭加法合成场地基岩地震动时程，给出了50年超越概率63%，10%和2%三种设防概率水平的合成场地基岩地震动加速度时程。每种概率水平各给出3条加速度时程。考虑到地震作用的随机性，根据GB 50111—2006（2009 版）《铁路工程抗震设计规范》相关规定及地震安全评价报告，选取50年超越概率为2%的3 条罕遇地震作用下的地震波（A波、B波、C波，见图4），进行地震响应分析。

图4 3条罕遇地震作用下的地震波

2.3 模拟结果与分析

2.3.1 不同工况下的减震效果分析

顺桥向分别输入3 条地震波，时程分析时取3 条地震波计算结果中的内力最大值作为该桥地震响应的理论计算值。中墩11#（西安侧），12#（延安侧）墩底截面内力计算结果见表1。

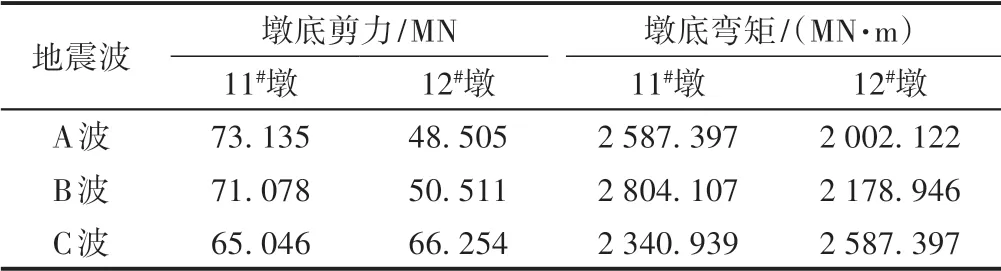
表1 中墩11#，12#墩底截面内力计算结果

为确定最优液体黏滞阻尼器参数，C分别取2，3，4，5，6 MN·（s/m）α，α分别取0.3 和0.4，组合为10 种工况，见表2。

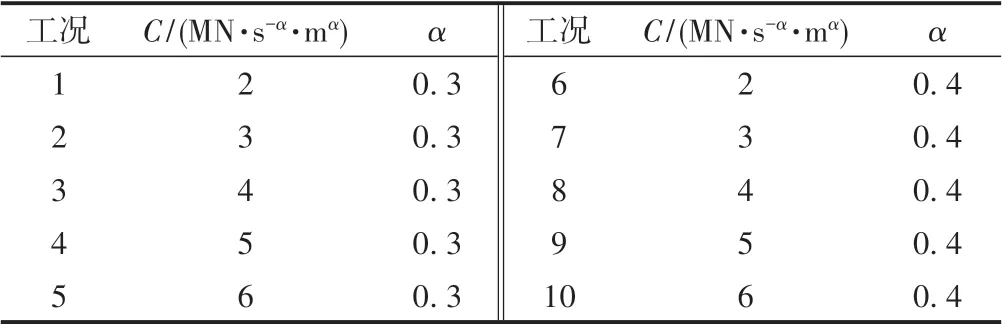
表2 各工况C，α的取值

限于篇幅，本文仅给出中墩11#，12#墩底内力随液体黏滞阻尼器参数（C，α）的变化情况，见表3—表4。未设置阻尼器时中墩11#，12#墩底弯矩分别为2856.064，2587.398 MN·m，剪 力 分 别 为73.135，66.255 MN。墩底内力均值为设置液体黏滞阻尼器后墩底内力的平均值。

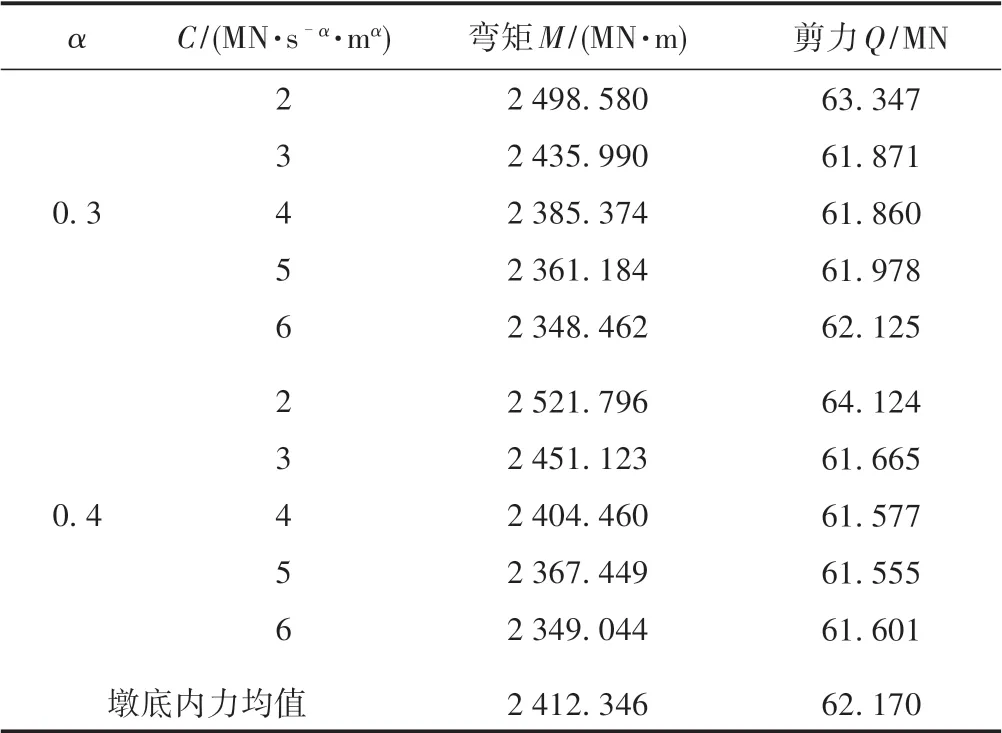
表3 11#墩的墩底内力随阻尼器参数变化情况

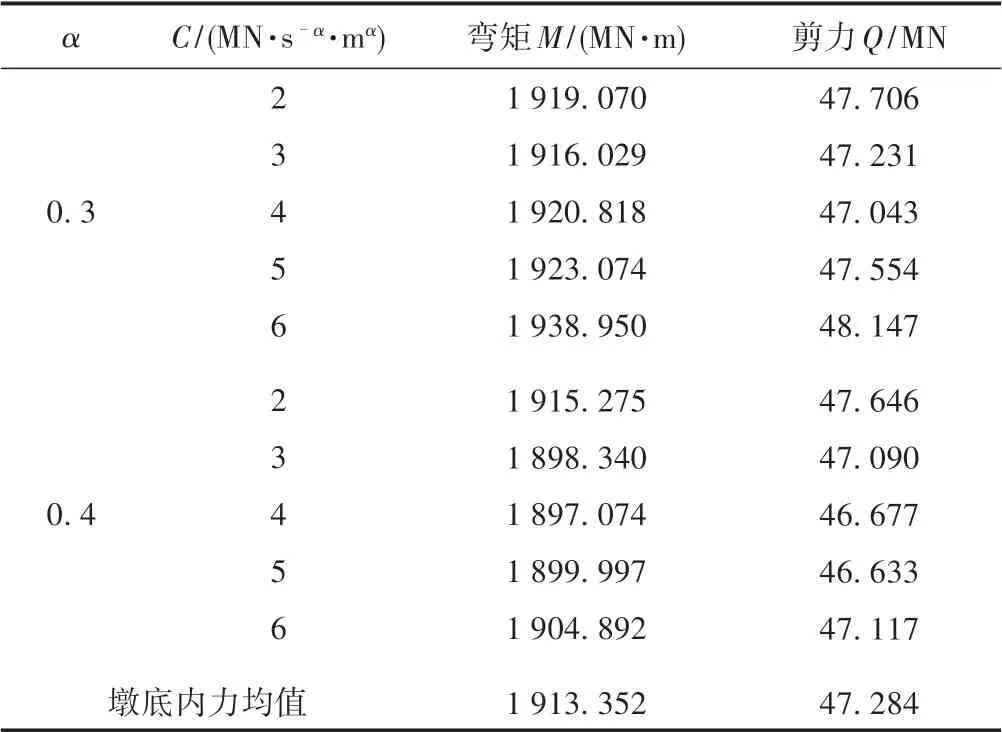
表4 12#墩的墩底内力随阻尼器参数变化情况

由表3—表4 可知：①设置液体黏滞阻尼器后，随着阻尼系数增大，11#墩的墩底弯矩单调递减，墩底剪力先减小后增大，12#墩的墩底弯矩和剪力均先减小后增大，但变化趋势不太明显。②设置液体黏滞阻尼器前后，11#，12#墩的墩底弯矩分别由2856.064，2587.398 MN·m 减小为2412.346，1913.352 MN·m（平均值），减幅分别为15.5%，26.1%。同理，剪力减幅分别为15.0%，28.6%。说明设置阻尼器后11#，12#墩的墩底弯矩和剪力均明显减小。③C＞3 MN·（s/m）α，α=0.4 时11#墩的剪力、12#墩的墩底弯矩和剪力减幅均比α= 0.3 时大，但C＞4 MN·（s/m）α，α= 0.4 时，12#墩的墩底弯矩和剪力小幅上升，对桥梁结构的减震效果变弱。④综合各墩墩底弯矩与剪力的减幅，C=4 MN·（s/m）α，α=0.4 时该连续刚构-拱组合桥的减震效果最佳。

设置液体黏滞阻尼器后主梁位移随阻尼器参数变化情况见表5。

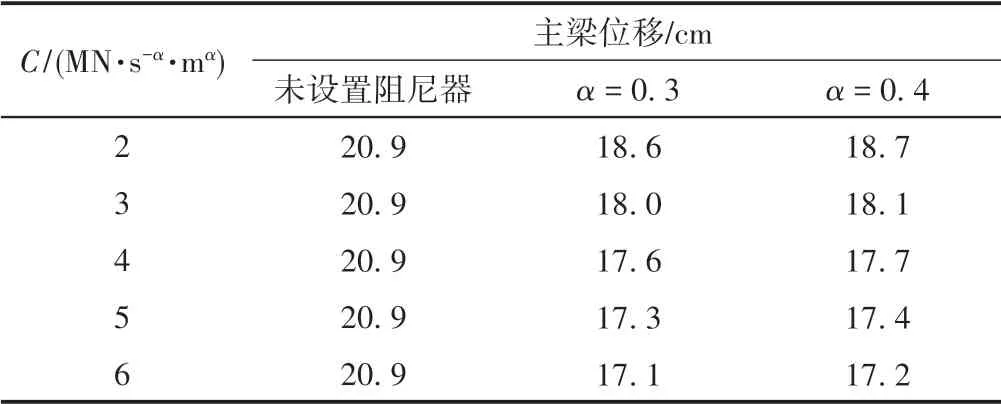
表5 主梁位移随阻尼器参数变化情况

由表5 可知：在顺桥向罕遇地震作用下主梁位移随着阻尼系数增大而逐渐减小。当C=4 MN·（s/m）α，α=0.3 时，主梁位移由未设置阻尼器时的20.9 cm 减至17.6 cm，减幅15.8%。α一定时，主梁位移随着C增大而减小；C一定时，虽然α= 0.3 时主梁位移比α=0.4时小，但幅值相对较小，二者差别不大。

综合考虑墩底内力及主梁位移，C=4 MN·（s/m）α，α=0.4时减震效果最优，故将其作为优化后的阻尼器参数。此时液体黏滞阻尼器的阻尼力为3200 kN。

2.3.2 采用优化参数后的减震效果

为分析所选液体黏滞阻尼器的减震效果，定义减震率=（未设置阻尼器时组合桥的墩底内力-设置阻尼器后组合桥的墩底内力）/未设置阻尼器时组合桥的墩底内力×100%。

设置液体黏滞阻尼器后顺桥向罕遇地震作用下墩底内力及减震率见表6。

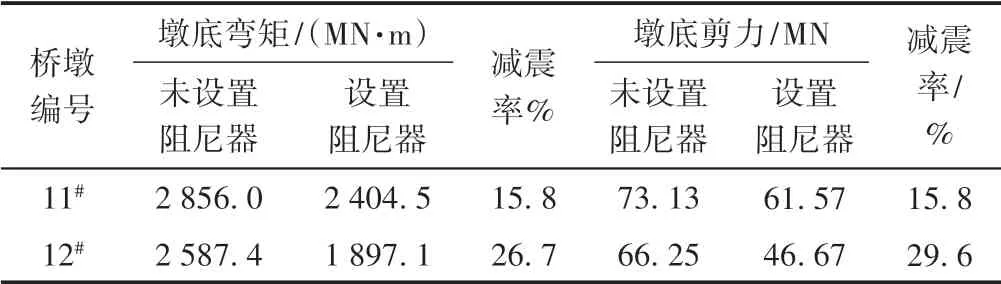
表6 墩底内力及减震率

由表6 可知：设置阻尼器后11#墩的墩底弯矩和剪力减幅均为15.8%；由于12#墩基础为明挖基础，12#墩的墩底弯矩和剪力减幅均在26% ～30%，减震效果较11#墩更明显。

4 结论

通过对设置液体黏滞阻尼器后西延高速铁路连续刚构-拱组合桥的减震效果分析以及对阻尼器参数的优化，得到以下结论：

1）随着阻尼系数增大，11#墩的墩底弯矩单调递减，墩底剪力先减小后增大，12#墩的墩底弯矩和剪力均先减小后增大，但变化趋势不太明显。随着阻尼系数增大，主梁位移逐渐减小，阻尼器的减震效果逐渐增强。综合考虑墩底内力及主梁位移，C=4 MN·（s/m）α，α=0.4时减震效果最优。此时阻尼力为3200 kN。

2）采用优化参数后，11#墩的墩底弯矩和剪力减幅均为15.8%，12#墩的墩底弯矩和剪力减幅均在26% ～30%。设置液体黏滞阻尼器后减震效果明显。