相交轴磁齿轮传动系统含内共振时的自由振动
2021-04-12王小猛郝文斌郝秀红
王小猛,郝文斌,郝秀红,*
(1.秦皇岛技师学院,河北 秦皇岛 066004;2.燕山大学 机械工程学院,河北 秦皇岛 066004)
0 引言
磁场调制型磁齿轮传动由于采用同轴式拓扑结构,永磁体利用率高,输出转矩大,机构转矩密度可高达150 kN·m/m3,传动能力在某种程度上可以与机械齿轮传动相媲美。由于采用磁场传递运动和动力,无接触、无磨损、无需润滑,克服了机械齿轮轮齿接触引起的疲劳折断,具有节能、维护成本低等优点[1-2]。
由于采用磁耦合作用使得构件间磁耦合刚度较机械轮齿间的机械啮合刚度小得多,系统某些模态频率较低[3-4]。郝秀红、Sina M等给出了磁耦合刚度的变化规律,分析了磁场调制型磁齿轮传动系统模态特征,明确了输入、输出转子扭转振动频率比调磁环的扭转振动频率低得多,但较传统平行轴磁齿轮高的结论[5-6]。Lee等采用有限元分析了磁场调制型磁齿轮传动的模态频率和模态振型,并通过仿真和试验研究了磁齿轮的低噪音特征[7]。磁齿轮传动由于构件间不存在摩擦阻力,电磁阻尼极小可以忽略,导致系统发生较大振动时衰减缓慢,且系统动力稳定性较差[8]。Gardner M C等提出了一种分析磁齿轮非线性动力学特性的模型和方法,并指出了增加黏性阻尼对提高系统振动衰减的重要性[9]。针对磁耦合刚度带来的问题,Frank N W等采用在转子中嵌入阻尼线圈的方式增加电磁阻尼以加速构件振动衰减[10],Montague R等通过在磁齿轮中置入位置伺服监控器的方法,通过精确控制构件的位置而间接达到加速系统振动衰减的目的[11]。但由于磁场调制型磁齿轮系统发展历史较短,国内外学者的研究主要集中于新型磁齿轮机构转矩特性分析、参数优化等方面的研究[12-13],但对于其稳定性等动力学方面的深入研究仍比较缺乏。
磁齿轮系统中各构件间的磁耦合力复杂,磁耦合刚度呈现出明显的非线性特性,且受传动比等参数影响会出现内共振现象,使得系统的动力学行为更为复杂。探索存在内共振时磁齿轮系统的动力学行为可以为提高系统稳定性,加速磁齿轮传动产业化奠定基础。
1 磁齿轮系统非线性动力学模型
磁场调制型相交轴磁齿轮传动主要由输入转子、输出转子及调磁体三部分组成,如图1所示。输入、输出转子端面分别均匀间隔布置有N1、N3块N、S极永磁体,直线型调磁体由N1+N3条导磁和非导磁材料间隔布置成椭圆环形,调磁体两端面呈一定角度(一般为90°),且端面截面形状为圆环形,与输入、输出转子端面上环形永磁体相对。调磁体端面与输入、输出转子上的永磁体端面平行,形成两层长度均匀的气隙。
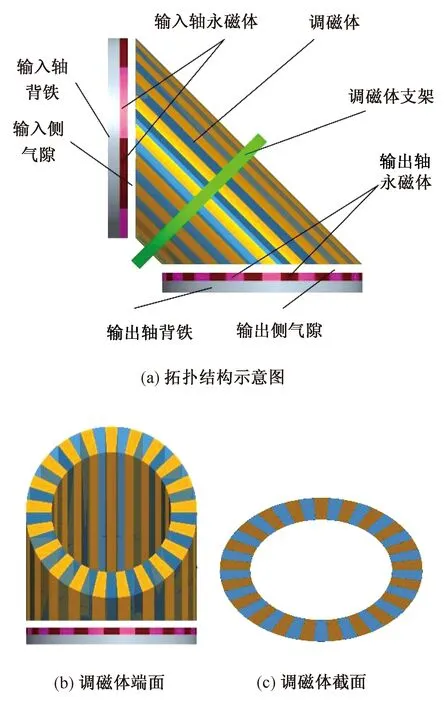
图1 调磁体直线型相交轴磁齿轮拓扑结构Fig.1 Structure diagram of the field modulated magnetic gear with intersecting axes
当输入转子回转时,永磁体在输入转子及调磁体间形成主谐波次数为N1的磁场,该磁场经调磁体调制后在输出转子与调磁体间的气隙中形成主谐波次数为N3的磁场,与输出转子上永磁体极对数N3相等,实现等磁极耦合并传递运动和动力。
相交轴磁齿轮传动系统非线性动力学模型如图2所示,输入转子与调磁体、调磁体与输出转子间采用磁力耦合,调磁体与其固定支架间的约束可以简化为沿切线方向的等效线性弹簧。考虑到各构件间的横向支撑刚度比扭转刚度大得多,本文只考虑各构件的扭转振动。

图2 相交轴磁齿轮非线性动力学模型Fig.2 Nonlinear dynamic model of the field modulated magnetic gear with intersecting axes
磁齿轮传动系统中各构件间为磁力耦合,忽略由于磁场调制引起的齿槽转矩波动,输入、输出转子上的转矩大小可表示为
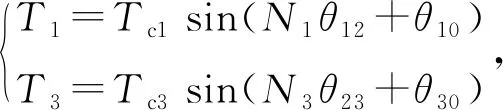
(1)
式中,T1、T3为输入、输出转子上的转矩;Tc1、Tc3为输入、输出转子上转矩的最大值;θ10、θ30为输入转子与调磁体、调磁体与输出转子间的初始相对旋转角;θ12、θ23为输入转子与调磁体、调磁体与输出转子间的相对扭转角位移。
各构件间扭转振动方向的磁耦合力可表示为

(2)
式中,FIs、Fso为输入转子与调磁体、调磁体与输出转子间的磁耦合力;R1、R3为输入、输出转子当量回转半径;θk为输入转子、调磁体和输出转子的扭转振动位移,k=1,2,3。
为方便起见,用各构件的扭转线位移代替其扭转角位移
x=[u1u2u3]T,
(3)
其中,uk=Rkθk。
构件间的磁耦合力为构件间相对扭转位移的函数,则将构件间的磁耦合力在t=0,即uk=0时刻展开为泰勒级数可表示为

(4)
其中,h1=Tc1sinθ10/R1,
h2=Tc3sinθ30/R3,
由式(4)可知,各构件的磁耦合力为构件间相对扭转位移的非线性函数。将构件间的磁耦合力展开为泰勒级数,忽略只会导致磁齿轮系统各构件静态变形的常数,由拉格朗日方程可得相交轴磁齿轮传动系统自由振动的非线性动力学微分方程为

(5)

将式(5)写为矩阵形式为

(6)
其中,M=diag(M1M2M3),
u=[u1u2u3]T,
c=diag(cIcsco),
F=[F1F2F3]T,
式中,M、u、c、k、F分别为质量矩阵、位移矢量、阻尼矩阵、刚度矩阵、等效载荷矢量。
以式(6)的线性派生系统为基础将式(6)正则化可得

(7)
式中,uN、kN、cN和FN分别为正则位移矢量、正则刚度矩阵、正则阻尼矩阵、正则等效载荷矢量。其中,
uN=[uN1uN2uN3]T,
FN=[FN1FN2FN3]T,
FNk=AN1kF1+AN2kF2+AN3kF3,
式中,ωk为磁齿轮传动派生系统各阶固有频率。
2 含1∶2内共振时自由振动公式推导
非线性系统的派生系统多个固有频率值相互可有理通约或接近于可有理通约时,系统就可能产生内共振。当系统输出转子旋转模态固有频率约等于输入转子扭转模态固有频率2倍时,引入下面的解谐参数
ω3=2ω1+εσ,
(8)
采用多尺度法求自由振动(7)的近似解析解。为使阻尼的影响与非线性的影响相均衡,从而使得阻尼相与非线性项在同一摄动方程中,对小而有限振幅的二阶近似解,其形式为
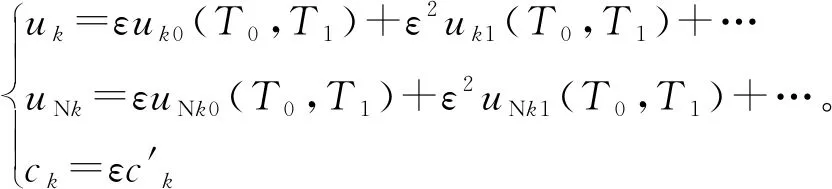
(9)
将式(8)和式(9)代入式(7)的自由振动方程,由方程两边小参数ε的同次幂系数相等,可得以下的近似线性微分方程组
ε阶

(10)
ε2阶

(11)
其中,FNk0=AN1kF10+AN2kF20+AN3kF30,

(12)
式中,Ak为初始位移,常坐标系下式(12)的解为
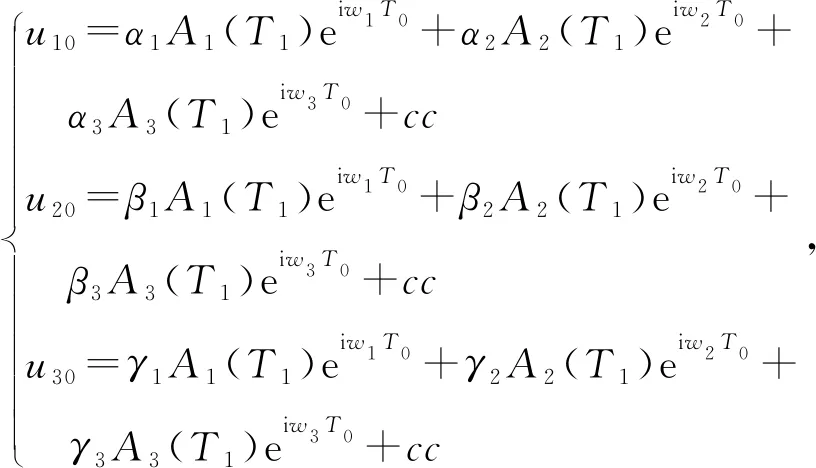
(13)
其中,α1=AN11,α2=AN12,α3=AN13,
β1=AN21,β2=AN22,β3=AN23,
γ1=AN31,γ2=AN32,β3=AN33。
将式(12)和(13)代入式(11)并消除久期项得

(14)
其中,P1=2ω1(AN11α1+AN21β1+AN31γ1),
S1=-AN11[2c1α1α3+e1(α1β3+α3β1)+
2d1β1β3]+AN21[2c1α1α3+2d1β1β3+
e1(α1β3+α3β1)-2c2β1β3-2d2γ1γ3-
e2(β1γ3+β3γ1)]+AN31[2c2β1β3+
2d2γ1γ3+e2(β1γ3+β3γ1)],
P2=2ω2α2AN12+2ω2β2AN22+2ω2γ2AN32,
式(14)中的第二式的解随T1的增加逐渐衰减为零,其解为
A2=E2e-R2T1/P2,
(15)
对于其他两项,设其解的形式为
Ak=Ek(T1)eiθk(T1),
(16)
将式(16)代入式(14)中的第一、第三式,并分离实部和虚部可得

(17)
其中,γ1=θ3-2θ1+σT1。
采用Runge-Kutta方法解式(17)中的各参数,其中E1、E3的初值与A1、A3相同,γ1初值为零。将所得E1、E3代入式(13)可以得到在常坐标系下的一次近似解析解。
3 磁齿轮系统自由振动分析
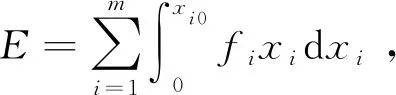

表1 磁齿轮系统参数Tab.1 Parameters of the magnetic gear
由图3可知,能量在两个模态间不断交换,且初始能量越高,即初始振幅越大能量交换越快。由于阻尼的作用模态振幅逐渐衰减,且能量交换的频率随着时间的衰减不断减小,即周期不断增加,这与能量越大振动波动越快相一致。
将如图3(a)的各模态振幅代入式(16)后连同式(15)代入式(13)可得系统时域响应曲线,同时,调整系统参数当系统不存在内共振时的振幅如式(15)所示,代入式(13)可得如图4所示。


图3 非线性系统正则坐标下C1、C3振动振幅Fig.3 Amplitude of C1 and C3 in normal coordinate

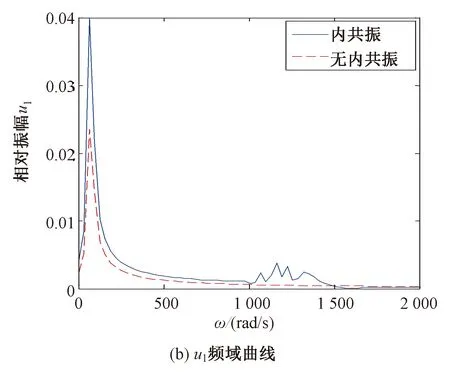
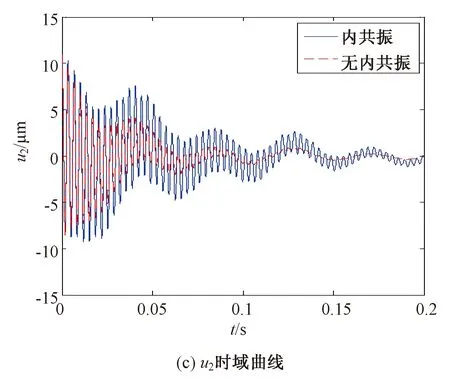
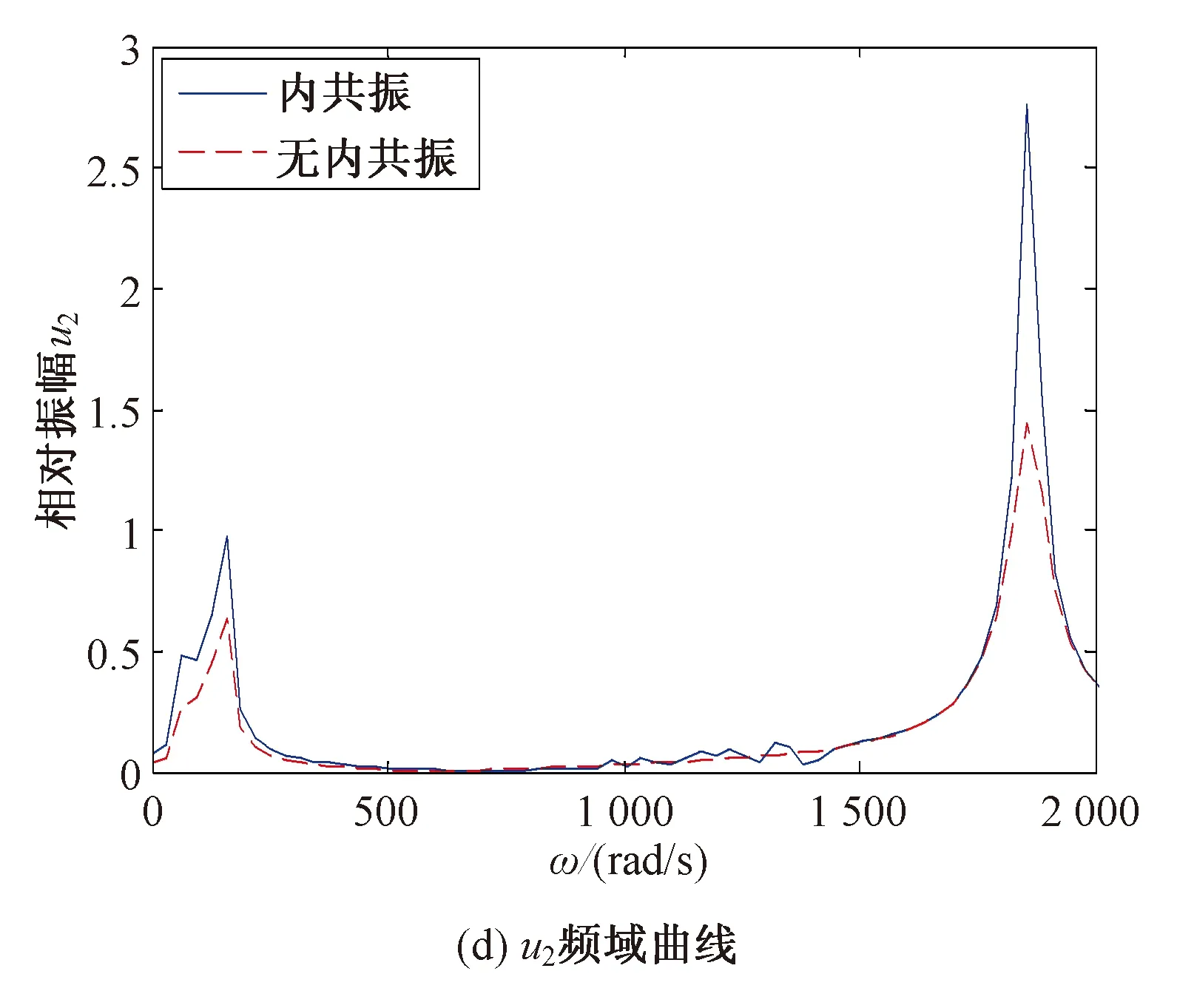
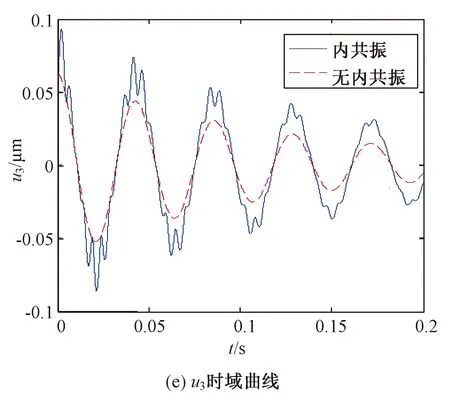

图4 磁齿轮非线性系统含内共振时的自由振动响应Fig.4 Free vibration response of the nonlinear magnetic gear system with the internal resonance
由图4可知,相交轴磁齿轮非线性系统中存在与不存在内共振相比,存在内共振时由于阻尼振动衰减较缓慢,且各构件衰减过程中均存在频率不断变化的能量交换。其中,输入、输出转子的振动衰减中由于彼此间的内共振关系,模态间的能量交换更加明显,调磁体由于扭转支撑刚度较大,能量交换相对不明显。输入转子、调磁体和输出转子振动位移中的主要频率分别为各自的模态频率,其次为有与内共振产生的能量交换频率,调磁体振动位移中还包含了与输入、输出转子的耦合频率。
模态间的内共振将使得各模态间影响明显,可利用这一影响使其与其他模态耦合的方式来调节某一模态振动衰减速度。例如可以通过在输入或者输出侧增加被动阻尼从而使输入和输出转子的振动同时加快衰减。
4 结论
考虑构件间磁耦合力非线性时,磁场调制型相交轴磁齿轮系统为含平方项的非线性系统,采用多尺度法得到了各模态振幅的微分方程,通过数值解法得到了各模态在不同初始能量时的变化曲线和系统自由振动响应曲线。当存在内共振时系统能量将在模态间不断交换传递,且交换频率随能量增大而加快。由于磁齿轮系统构件间非接触性导致的弱阻尼,内共振的存在将导致各构件在外部激励消失后衰减更加缓慢,恶化系统的动力学性能。各构件的主导频率为各自对应的模态频率,其次为能量交换频率。由于磁齿轮系统的磁耦合刚度和弱阻尼特点,必须采用添加被动阻尼或半主动阻尼的方式加快衰减速度,将是后续的重要研究内容。
