大型铝合金筒节轧制过程圆度控制及影响因素分析
2021-04-12孙孟乾孙建亮
孙孟乾,孙建亮,*,韩 辉,彭 艳
(1.燕山大学 国家冷轧板带装备及工艺工程技术研究中心,河北 秦皇岛 066004;2.京东方科技集团股份有限公司,北京 100015)
0 引言
由于铝合金密度小、比强度高、质量轻、导热性好、延展性好、易成形,可100%回收,广泛应用于航空航天和汽车等领域[1]。大型铝合金筒节零件是航空航天工业、风电和军工装备的关键结构件,其受力状态复杂、尺寸精度和综合性能要求高,对制造工艺的要求很高,目前相关领域对于大型高强度精密铝合金筒节的需求迫切。国际上,该筒节的制造通常采用分段型材拼焊方案,该方案的优点是材料来源简单、技术难度小,但焊接接头强度低,存在焊接变形、残余应力大、形状和力学性能一致性差等缺陷[2-3]。为了解决这些问题,发达国家纷纷研发整体锻环,其减重效果明显,使用寿命、可靠性、可维护性明显提高。圆度精度是筒节轧制过程的关键控制指标,随着筒节直径的增大,筒节圆度精度的控制难度大大增加。关于大直径筒节轧制和圆度控制的研究,张淑莲研究了超大直径铝合金环件轧制工艺和装备,轧制出直径5 m的高强度铝合金环件[4]。潘剡等设计了Φ9 m超大型环件轧制工艺参数,针对超大型环件轧制变形特点提出了一种新的进给规范,并进行了有限元模拟,但并未对环件圆度控制进行研究[5]。FOROUZAN提出了一种计算方法用于环件轧制导向辊控制过程仿真,可精确模拟导向辊对环件的影响,大大提高计算效率[6]。兰箭等研究了导向辊对冷轧环件圆度误差的影响规律[7]。WANG等研究了轧辊的运动对大型钛合金环件尺寸精度的影响[8]。WANG等研究了各种导向辊控制模式对碾轧环件直径变化规律的影响,并提出一种基于光栅和PLC的可靠的位移测量装置[9]。LI等提出一种液压调节机构的导向辊控制方法,给出了机构的详细设计参数,并进行了有限元仿真模拟[10]。陈素文通过研究大型筒节轧制过程金属变形和温度演变规律,给出不同轧制工艺参数对金属变形影响,为产品质量控制提供了一定依据[11]。陈潇研究了筒节轧制过程热-力耦合,推导出筒节极限抱辊力理论公式,缩短了大型筒节轧机研发周期并节约研究成本[12]。
上述研究为大型筒节圆度控制机理研究提供了很好的基础,但大部分研究都是针对小型环件导向辊控制装置和控制方式的研究。目前国内已有企业研制出大型筒节轧机[13],该轧机采用双驱动辊轧制,筒节卧式布置,已经实现加氢反应器用钢筒节轧制,但目前该轧机轧制筒节圆度控制机理研究较少,对于大型铝合金筒节轧制成形和圆度影响因素的研究更少。本文针对6061大型铝合金筒节轧制成形过程,基于有限元法和实验方法研究了铝合金筒节轧制过程圆度最优控制方式及其影响因素。
1 筒节圆度评定方法
圆度是大型铝合金筒节轧制过程的重要产品质量控制指标。由于在轧制过程中筒节金属变形的非线性、轧制工艺和导向辊控制不当等问题,都可能导致圆度超差,因此实际生产中需要弄清筒节轧制过程中的圆度变化机理,制订圆度控制方案。目前圆度误差的计算方法主要有:最小二乘圆法、最小区域圆法、最大内切圆法和最小外接圆法。最小区域圆评定准则所评定的圆度误差值最小,且具有唯一性,本文采用最小区域圆法进行圆度误差的评定,即作一个外包容圆和与之同心的内包容圆去包容实际圆轮廓,两同心圆的半径差值即圆度误差。采用基于最小条件原则的最小区域圆法评定圆度误差的方法如下:如图1所示,O是实际轮廓图形的坐标原点,Pi(xi,yi)(i=1,2,…,n)为i个测得的点坐标值,O′为最小条件圆心,坐标为(a,b),令目标函数F(a,b)
F(a,b)=Rmax-Rmin=

(1)
式中,Rmax和Rmin是从(a,b)点到轮廓最远和最近点的半径;(xmax,ymax)和(xmin,ymin)为最远和最近点相对应的坐标。
优化计算F(a,b)的最小值Fmin时,则此时的(a,b)就是满足条件的最小区域圆的圆心坐标值,而Fmin就是圆度误差值。圆度误差越小,筒节圆度越良好。
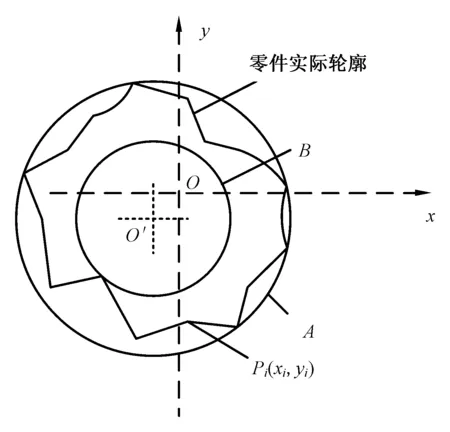
图1 最小区域圆法圆度误差评定的原理图Fig.1 Schematic diagram of the roundness error evaluation of the minimum area circle method
2 大型铝合金筒节轧制有限元模型
2.1 6061铝合金变形抗力模型
铝合金材料选取6061铝合金,属于Al-Mg系合金,主要成分如表1所示。本文以6061铝合金为研究对象,采用轴对称等温压缩法在Gleeble-3800热模拟实验机上进行热模拟实验,获得其真应力-真应变曲线。实验圆柱试样尺寸:直径10 mm,高15 mm。实验方案:以10 ℃/s的加热速度将试件加热到500 ℃,保温5 min,使试样的奥氏体均匀化,然后以5 ℃/s的冷却速度冷却至变形温度,保温2 min使试件温度均匀化,最后以不同的变形温度和变形率进行热压缩实验,变形温度取为250 ℃、300 ℃、350 ℃、400 ℃、450 ℃,应变速率取为0.001 s-1、0.01 s-1、0.1 s-1、1 s-1、10 s-1,真应变为0.7。为了减小因摩擦而引起实验误差,采用石墨和机油的混合润滑剂涂抹在试样两端进行润滑。

表1 6061铝合金材料成分(质量分数)
6061铝合金的稳态应力σs可以表示为

(2)
采用新型流变应力方程对变形抗力模型进行表示

(3)
为了验证模型的拟合精度,将所建模型的计算结果和实验测试结果进行比较,如图2所示,可知模型精度误差低于10%,满足工程要求。

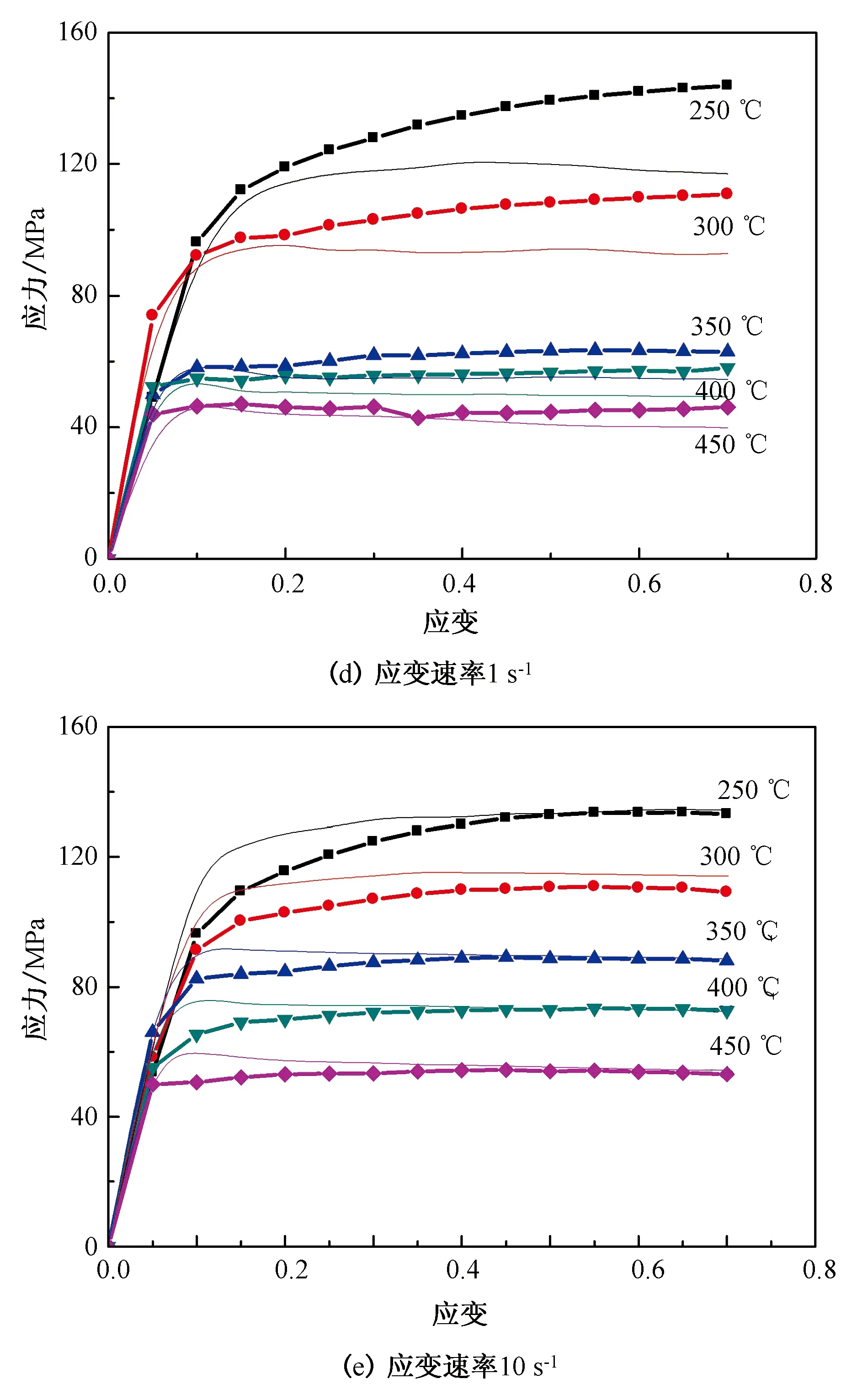
图2 模型计算结果和实验测试结果对比图Fig.2 Comparison of model calculation results and experimental test results
2.2 基于DEFORM的大型铝合金筒节轧制仿真模型
大型铝合金筒节轧制时,筒节从上辊装入,上、下轧辊均为主动辊,下轧辊作旋转运动,上轧辊作压下运动和旋转运动,筒节在上下轧辊的连续碾压下发生塑性变形,本文考虑到筒节坯料锻造锥度问题,基于DEFORM软件建立轧制过程有限元模型如图3所示。由于筒节尺寸巨大,为节约计算资源,计算时将大型铝合金筒节定义为弹塑性体,筒节材料为6061铝合金材料,将在Gleeble-3800上测得的6061铝合金变形抗力曲线导入到DEFORM材料定义模块中;上、下轧辊为驱动辊,导向辊为被动辊,上下轧辊和导向辊定义为刚体。轧制过程中上轧辊与筒节内表面、下轧辊与筒节外表面以及左、右导向辊与筒节外表面均发生接触,上、下轧辊与筒节内外表面接触采用剪切摩擦模型,导向辊为被动辊,不承受摩擦力矩。采用DEFORM软件划分网格,网格为四面体单元,筒节网格单元数为10万。利用其网格自动重划分功能,当模拟过程中单元发生畸变或者发生干涉时,软件进行自适应网格划分。轧制过程仿真参数如表2所示。

图3 大型铝合金筒节轧制过程有限元模型Fig.3 Finite element model for rolling process of large aluminum alloy cylinder

表2 轧制过程仿真参数Tab.2 Simulation parameters of rolling process
3 大型铝合金筒节轧制过程有限元仿真分析
3.1 轧制过程仿真
图4是温度为400 ℃情况上下轧辊的轧制力曲线。由图4可知各道次轧制中轧制力变化情况,在25 s及55 s中出现的轧制波动是由于此时筒节处于轧制道次的过渡阶段,压下系统进行压下;第二道次压下量为38.4 mm,第三道次压下量为64 mm,由于第三道次压下量较大,所以第三道次的轧制力较大;上、下两轧辊的轧制力大小相差不大,上辊轧制力略大于下辊轧制力。以400 ℃情况下FEM模拟轧制力与模型计算轧制力结果对比为例,轧制力计算值根据作者提出的计算模型得到[14],两种轧制力计算结果和计算误差如表3所示,由表3可知,计算轧制力和模拟轧制力的误差在10%以内,间接证明了有限元模型的正确性。

图4 400 ℃轧制中随时间变化的上、下辊轧制力Fig.4 Rolling force of upper and lower rolls changing with time in 400 ℃ rolling

表3 轧制力对比Tab.3 Rolling force comparison
图5是筒节轧制的圆度误差曲线。由图5可知,随着各道次筒节压下量的增大,筒节圆度误差总体上呈现增大的趋势,最终可达到100 mm。在第二道次结束时,筒节圆度误差达到了此道次的最大值,筒节变形不均匀;第三道次压下量较大,筒节圆度误差增大;第四道次压下量为25.6 mm,筒节圆度误差基本处于稳定状态,筒节变形逐渐均匀化;经过最后道次的成圆整形阶段,圆度误差将会相应减小,圆度得到改善。

图5 铝合金筒节轧制圆度误差曲线Fig.5 Aluminum alloy tube section rolling roundness error curve
3.2 大型铝合金筒节圆度影响因素分析
3.2.1不同导向辊控制模式下筒节圆度分析
目前大型筒节圆度控制主要是通过轧制工艺参数和导向辊综合控制的方式。导向辊控制包括位置控制方式和力控制方式,本文采用导向辊位置控制方式。导向辊位置的控制方式有3种:固定导向控制模式、定向导向控制模式和圆弧导向控制模式[15]。固定导向辊模式即通过固定导向辊位置来进行控制;定向导向控制模式,即定义导向辊的运动方向和速度,保证运动过程中导辊与筒节圆心的连线与竖直方向的夹角保持一定;圆弧导向控制模式,即导向辊沿着筒节外圈进行圆弧运动。本文主要研究轧制工艺参数和不同导向辊控制方式综合作用对轧制过程中筒节圆度的影响,进而确定最优控制方案。
图6为3种导向辊控制方式下筒节圆度误差曲线。由图6可知,采用固定导向辊控制方式时筒节圆度误差较大,且随轧制过程的进行圆度误差逐渐增大;采用圆弧形导向辊控制方式的轧制筒节圆度误差较小,随着轧制过程的进行圆度误差增大到一定程度出现拐点,之后圆度误差逐渐减小;定向导向辊控制方式圆度误差结果与圆弧形导向辊控制方式规律相似,但圆度误差更小,因此采用定向导向辊控制方式效果最佳。
图7为三种导向辊控制方式筒节轧制的应变场分布。由于轧制过程中筒节外表面等效应变最大,其次为筒节内表面,心部的金属等效应变最小,当筒节芯部及内外表面变形量差值越小,筒节的变形均匀程度就越好,表明该种导向辊控制方式较好。由图7可知,固定导向辊轨迹控制时筒节最大最小等效应变为0.491/0.057 3,变形均匀性较差;圆弧形导向辊轨迹和定向导向辊轨迹控制时筒节最大最小等效应变分别为0.517/0.060 3及0.464/0.059 7。由此可知,轧制过程中定向导向辊控制方式筒节变形均匀程度最好。因此,下述模拟中导向辊控制方式均采用定向导向辊轨迹控制方式。

图6 三种导向辊控制方式下筒节圆度误差曲线Fig.6 Cylindrical roundness error curve under three kinds of guide roller control modes
3.2.2轧制速度的影响
大型筒节轧制中,上、下轧辊均为驱动辊,即双驱动辊机制,这与普通碾环机采用的单辊驱动机制不同。根据转速与咬入条件和锻透条件的关联机制,可得上轧辊的转速范围:
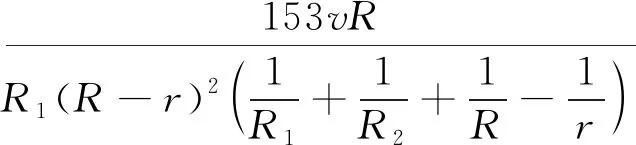
(4)
下轧辊的转速范围:

(5)
其中,R1是上辊半径,R2是上辊半径,R是筒节外半径,r是筒节内半径,v是轧辊转速,β是摩擦角。
图8是不同轧辊转速下筒节圆度误差曲线。由图8可知,随着轧辊转速的增大,筒节的圆度误差逐渐增大。当轧辊转速较大时,不利于筒节良好圆度的成形;轧辊转速较小时,会造成筒节轧制生产效率低。为保障筒节轧制圆度质量以及生产效率,应该在轧辊转速合理的区间内,取相对较小轧辊转速。
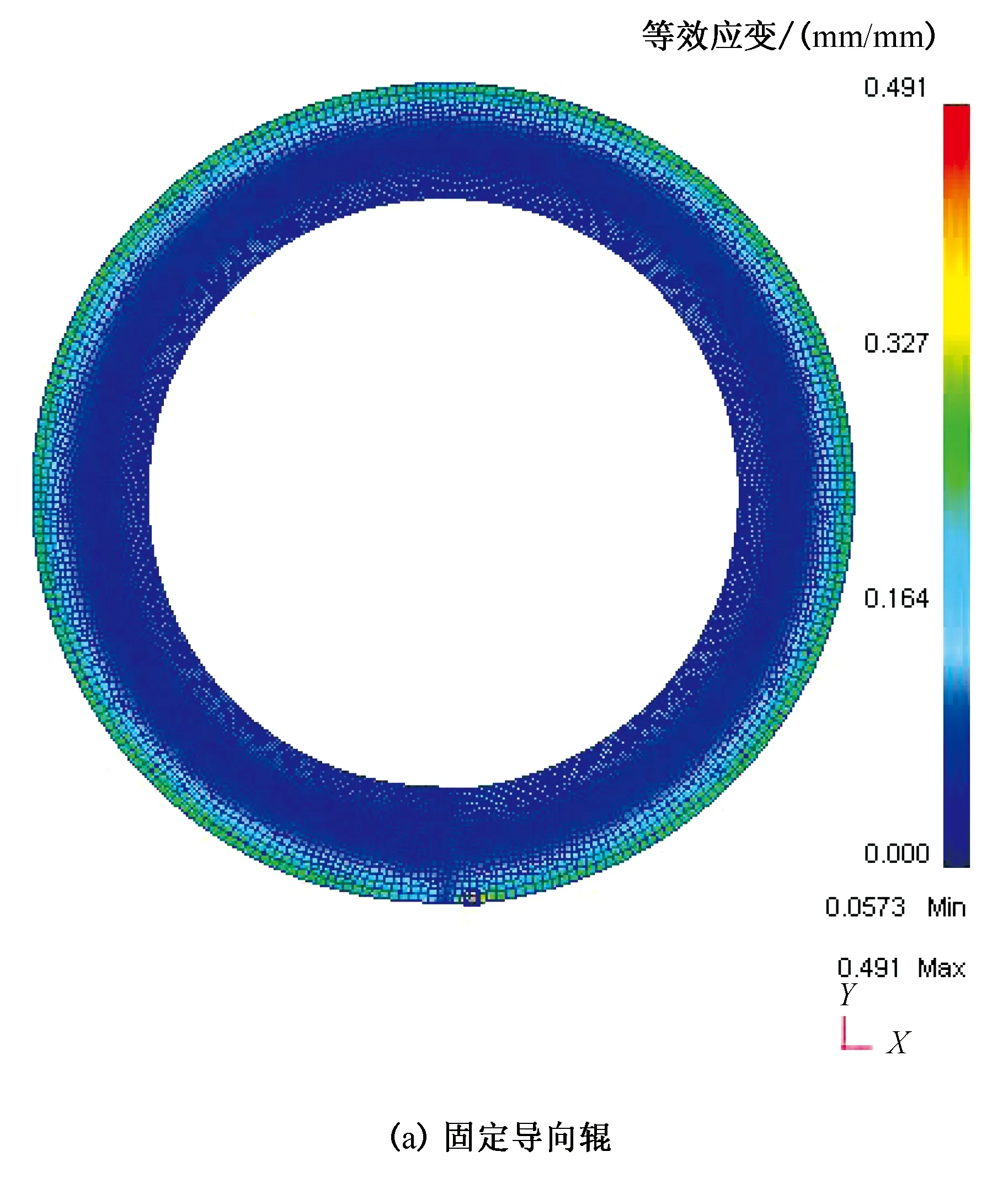
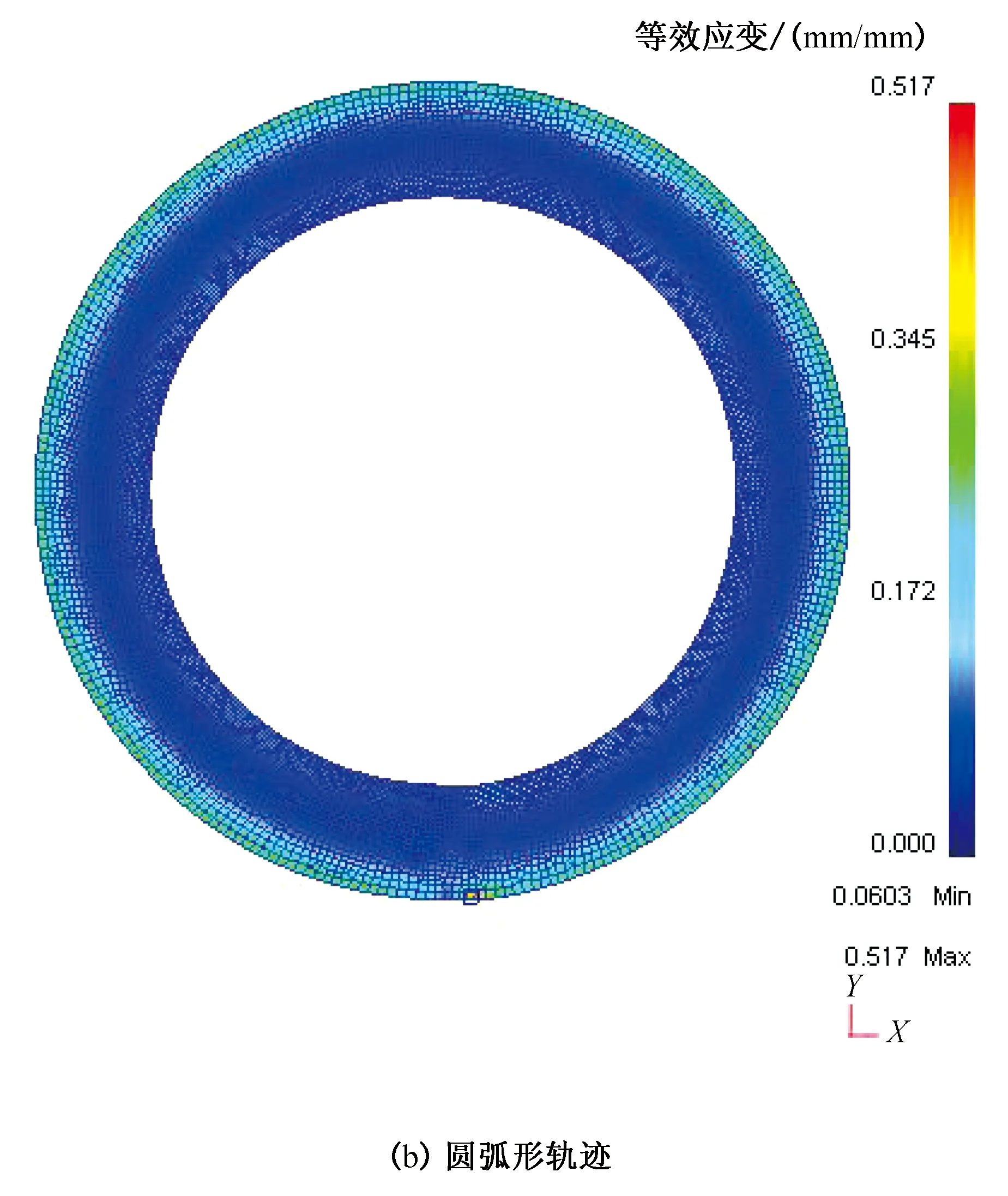

图7 3种导向辊控制方式下筒节应变场Fig.7 Strain field of cylindrical section under three kinds of guide roller control modes

图8 不同轧辊转速情况下筒节圆度误差曲线Fig.8 Roundness error curve of cylinder section with different roll speeds
3.2.3轧制温度的影响
针对大型铝合金轧制时的合理温度范围,选取轧制温度为300 ℃、350 ℃和400 ℃,对筒节轧制过程进行模拟。图9是不同温度情况下筒节圆度误差曲线。由图9可知,随着温度的增大,筒节的圆度误差变化较为不明显,三组间圆度误差值相差不太大。但从统计数据看来,温度在400 ℃时筒节圆度误差相对较小,因为当升高温度,压下量相同时,筒节心部的应变量会增大,变形均匀程度相对较好,因此,在合理的温度范围内,升高温度,筒节变形均匀化程度提高,筒节圆度质量相对较好。
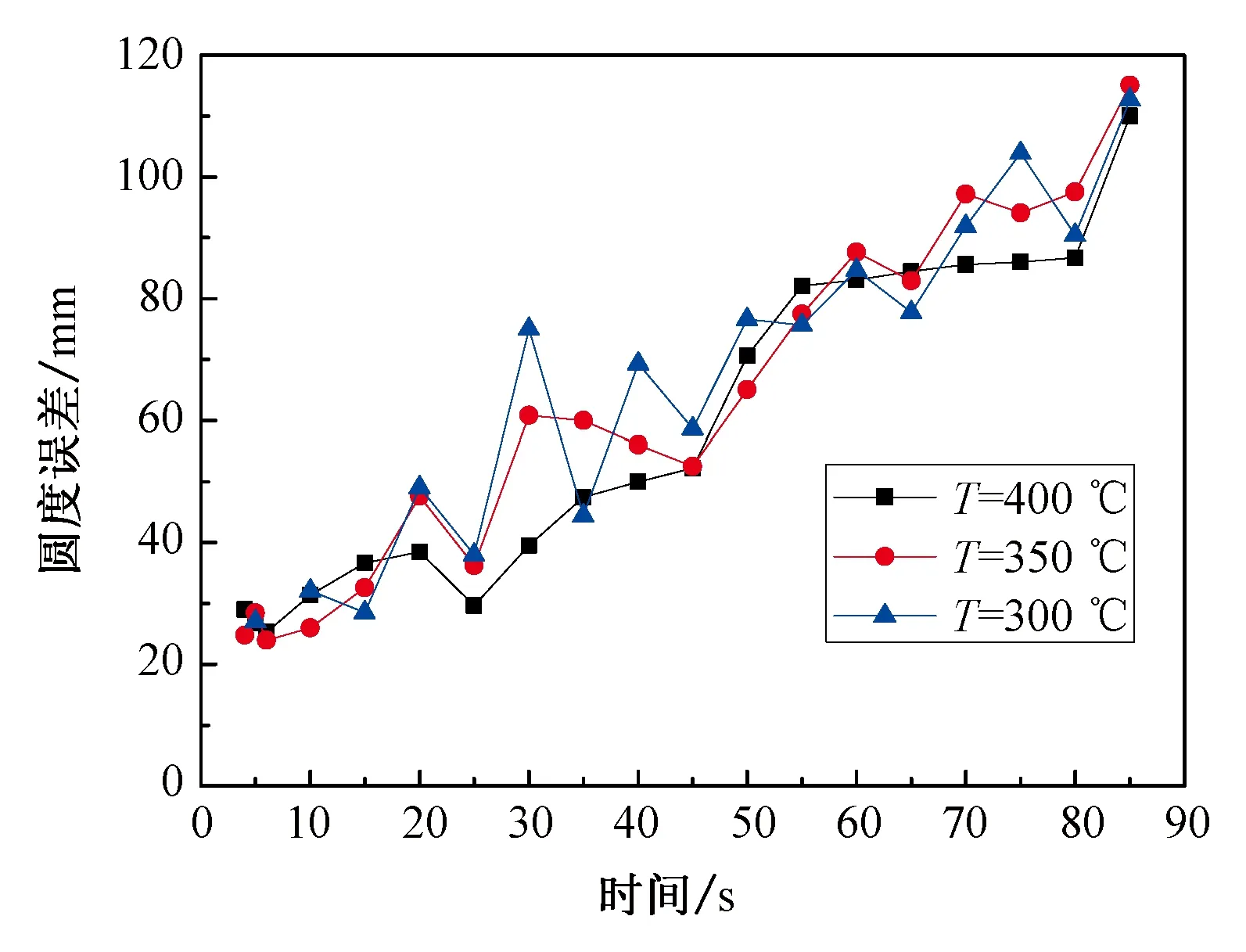
图9 不同温度下筒节圆度误差曲线Fig.9 Roundness error curve of cylinder section with different temperature
3.2.4轧制偏心距的控制效果
轧制初始时筒节轧机上下轧辊的圆心通过一条垂线,为了控制筒节的圆度,可将上、下轧辊在水平方向上施加一个偏距,即轧辊偏心距控制。该控制方法是参考板带轧制中异步轧制,在理论和工业应用上具有可行性。在初始模型的基础上,对筒节进行压下量为38.4 mm的轧制。给定左、右偏心距5 mm、10 mm、15 mm进行模拟,左偏距即沿轧制出口的相反方向给定上、下轧辊一偏距,右偏距即沿轧制出口方向给定上、下轧辊一偏距。图10是不同偏心距情况下筒节圆度误差。由图10可知,通过在轧制过程中给定不同大小的偏心距,轧制过程中筒节的圆度误差在一小范围内上下浮动,偏心距调整对整个筒节轧制过程的圆度误差控制效果一般。但由于筒节为封闭零件,筒节不同区域的圆度不一样,可能呈现椭圆形或不规则形状,轧制过程中对筒节的不同位置,通过在线调节轧辊偏心距可以达到实时调节筒节圆度的目的。
4 结论
本文针对6061大型铝合金筒节轧制成形过程圆度控制进行研究,建立了轧制过程有限元模型,并进行了模型验证,分析了大型铝合金筒节轧制过程圆度控制模式和影响因素,主要结论如下:1)采用定向导向辊控制方式筒节圆度误差最小,筒节变形均匀性好,圆度误差控制效果最佳;2)随着轧辊转速的增大,筒节的圆度误差逐渐增大;3)温度对筒节的圆度误差影响不大;4)偏心距调整对整个筒节轧制过程的圆度误差控制效果一般,但轧制过程中对筒节的不同位置,通过在线调节轧辊偏心距可以达到实时调节筒节圆度的目的。
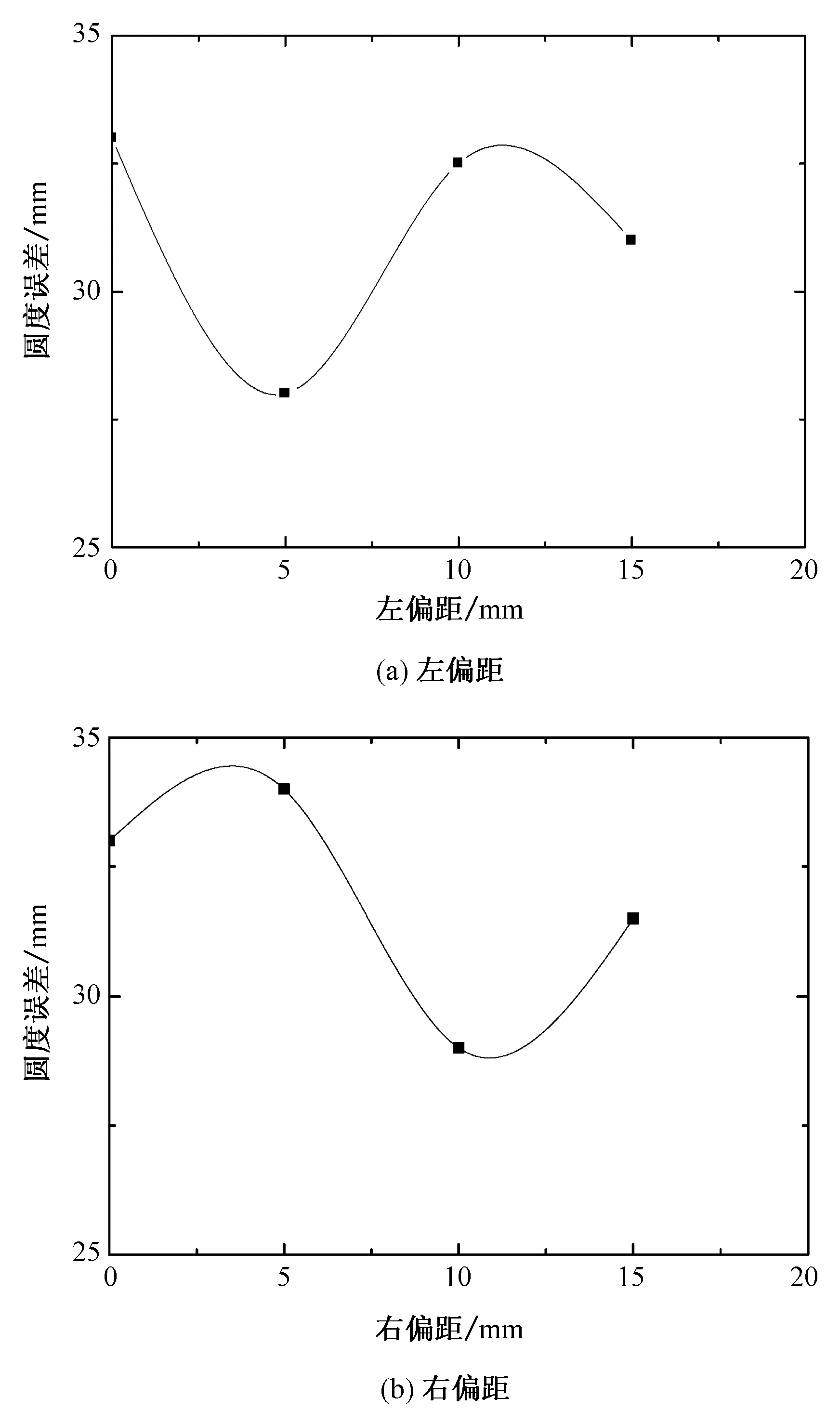
图10 不同偏心距情况下筒节轧制圆度误差结果Fig.10 Roundness error results of barrel rolling under different eccentricities
