输出误差约束的非线性系统的预定性能反步控制及应用
2021-04-12高红梅华长春阴良魁
高红梅,王 芳,*,华长春,宗 群,阴良魁
(1. 燕山大学 理学院, 河北 秦皇岛066004;2. 燕山大学 电气工程学院,河北 秦皇岛 066004;3. 天津大学 电气自动化与信息工程学院,天津,300072;4.中国科学院科技创新发展中心,北京 100190)
0 引言
随着控制理论的发展,非线性系统在实际工程中的应用越来越广泛,针对其控制的研究也取得了丰富的研究成果[1-6]。而不确定参数、外界干扰等的影响是控制实际工程系统时必须要考虑的因素,常用的方法有滑模控制[7]、干扰观测器[8-11]、智能控制[12-14]等。
许多工程系统,如飞行器系统、轧机系统、电机系统等除了需要考虑控制系统的稳态性能方面的要求,同时要考虑暂态性能的要求。预定性能控制解决了这个问题[15-17]。文献[15]针对带有干扰的单输入单输出反馈线性化系统设计了预设性能控制器。文献[16]进一步将研究成果推广到多输入多输出反馈线性化系统。针对一类单输入单输出非线性系统,文献[17]在误差转换的基础上,设计了预定性能控制器,但是控制器设计较为复杂。针对未知控制增益下的不确定非线性系统,文献[18]结合反步控制和神经网络设计了预定性能控制器。文献[19]考虑状态和输入受限的非线性系统,结合反步控制,设计了预定性能反步控制器。文献[20]针对单输入单输出严反馈系统,提出了输出反馈预定性能控制策略,但是,没有考虑外界干扰和执行器故障。文献[21]考虑了执行故障影响下非严格反馈系统的容错控制问题,基于模糊逻辑、反步控制和有限时间控制,设计了实现系统半全局有限时间稳定的容错控制器。文献[22]针对一类不确定非线性系统的容错控制问题,通过RBF神经网络处理执行器故障,设计了主动容错控制策略。文献[23]针对电动汽车车用永磁同步电机的车速跟踪问题以及由复杂路况引起的负载扰动问题,利用遗传算法优化鲁棒H∞控制器中的加权函数,提出自适应鲁棒非线性控制策略。通过引入控制参数在线自适应调整技术,保证控制器对参数、干扰具有很强的鲁棒性。
本文综合考虑输出误差约束、不确定参数、外界干扰和执行器故障影响下的非线性系统的跟踪控制问题。在反步控制框架下,结合障碍Lyapunov函数和干扰观测器,设计预定性能反步控制器。 将虚拟控制输入的导数、外界干扰和执行器故障作为综合不确定,并通过设计干扰观测器对其进行估计,解决传统反步控制中的 “计算爆炸” 问题,避免采用滤波器,简化控制器的设计结构。通过自适应估计故障因子,解决执行器故障问题。采用Lyapunov理论证明闭环系统的稳定性以及跟踪误差满足预设的性能。最后,通过永磁同步电机系统的跟踪控制仿真验证所设计的控制策略的有效性。
1 问题描述
考虑如下非线性系统:
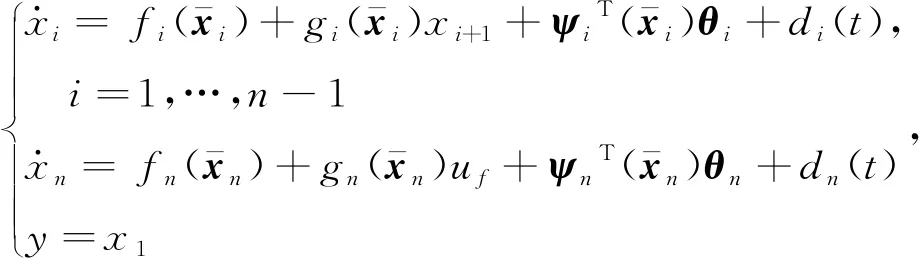
(1)
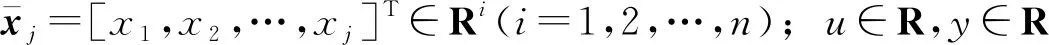
执行器故障在实际中是不可避免的,主要包括卡死、漂移、失效等,可以描述为如下参数化形式:uf=λfu+ρ,其中,λf为执行器效率因子,0≤λf≤1,表示执行器在失效后仍然有效的比例,ρ表示偏差故障,当λf=1,ρ=0时,执行器是正常的(无故障发生);当λf=0时,执行器完全失效;当0<λf<1时,执行器部分失效。
控制目标:对于系统(1),结合障碍Lyapunov函数、干扰观测器与反步控制设计预定性能控制器,实现输出跟踪其参考指令yd; 且跟踪误差满足预设的性能。
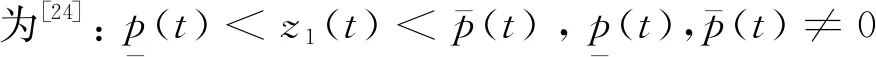
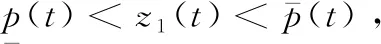
为了防止输出违反约束条件,引入障碍Lyapunov函数,定义如下:
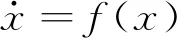
在设计控制器之前,给出如下假设和引理:
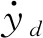
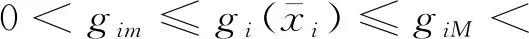
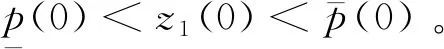
假设4 外界干扰di(t)满足
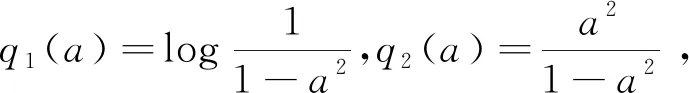
引理2[26]考虑系统
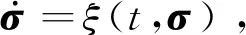
(2)
σ=[ω,a]T∈N,M={a∈R:|a|<1}⊂R,N=Rl×M⊂Rl+1是一个开集。函数ξ:R+×N→Rl+1在R+上分段连续,且在N内关于σ满足局部Lipschitz条件。假设存在连续可微的正定函数Θ:Rl×R+→R+,ϑ:M→R+。满足|a|→1,ϑ(a)→;β1(‖ω‖)≤Θ(ω,t)≤β2(‖ω‖), 式中,β1,β2为K类函数。令
V(σ)=ϑ(a)+Θ(ω,t),a(0)∈M,
(3)
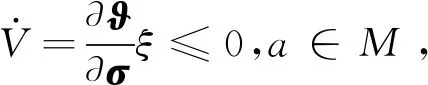
2 控制器设计
将uf=λfu+ρ代入式(1),转化为如下形式:
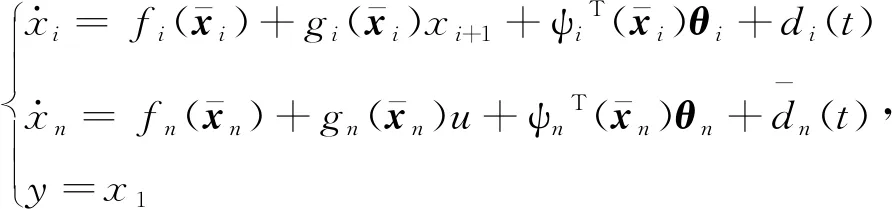
(4)
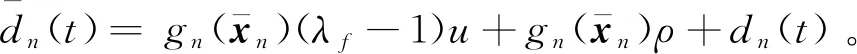
接下来,我们将在反步控制的框架下基于式(4)设计控制器,设计过程包括n步:前n-1步设计虚拟控制输入,其中,第一步中需要设计障碍Lyapunov函数保证输出误差的预定性能,最后一步设计实际控制输入u。在控制器设计过程中,通过自适应律处理不确定参数;并采用干扰观测器估计综合不确定项,同时处理外界干扰、执行器故障和传统反步控制的“计算爆炸”问题。
Step 1 设计虚拟控制输入α1。
定义输出跟踪误差为
z1=x1-yd,
(5)
由式(5),z1关于时间的导数为
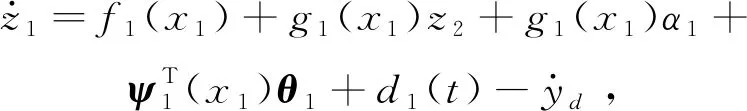
(6)
选择如下Lyapunov函数
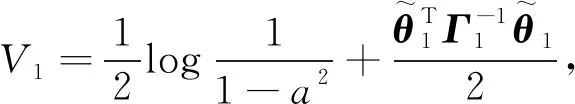
(7)
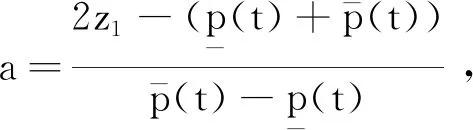
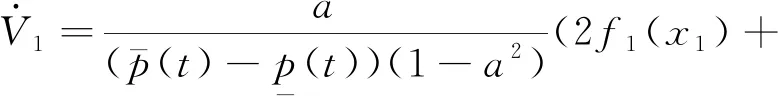
(8)
设计如下干扰观测器估计d1(t)
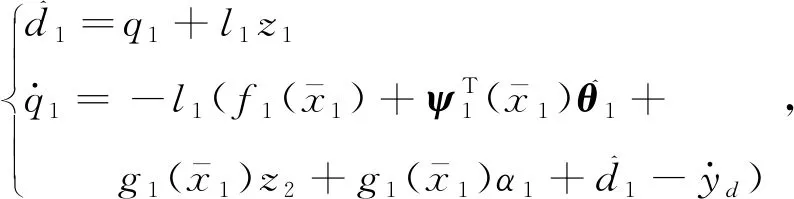
(9)
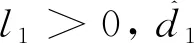
基于干扰观测器(9),设计虚拟控制输入α1
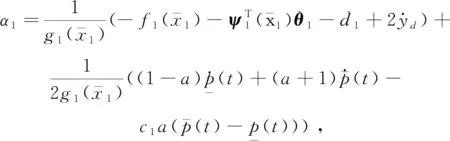
(10)
θ1的自适应律为
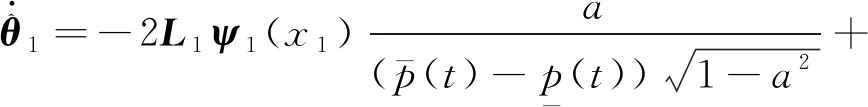
(11)
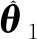
注2:本文所设计的干扰观测器不仅处理了外界干扰和执行器故障,同时通过将虚拟控制输入的导数作为综合不确定的一部分,解决了传统反步的 “计算爆炸” 问题,不需要通过微分器或者滤波器解决“计算爆炸” 问题,因此简化了控制器结构。
Step 2 设计虚拟控制输入α2。
定义x2的误差信号为z2=x2-α1,它关于时间的导数为
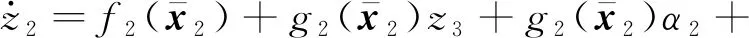
(12)
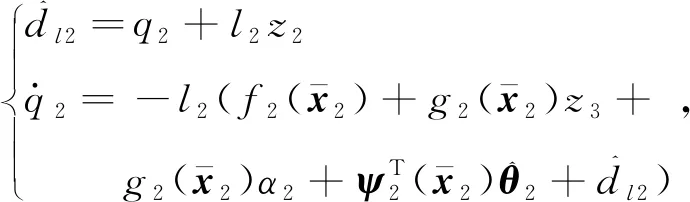
(13)
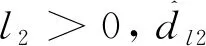
基于式(12)和式(13),设计虚拟控制输入α2为
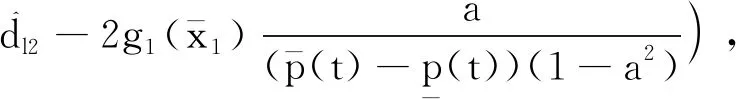
(14)
θ2的自适应律为
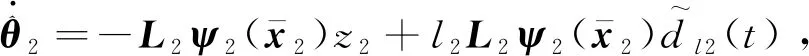
(15)
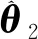
Stepi设计虚拟控制输入αi(3≤i≤n-1)。
定义xi的误差信号为zi=xi-αi-1,关于时间的导数为
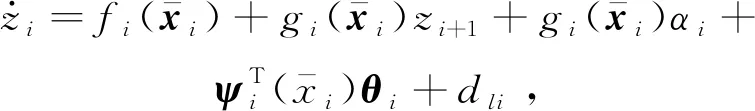
(16)

(17)
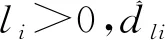
基于式(16)和式(17),设计虚拟控制输入αi为

(18)
θi的自适应律为
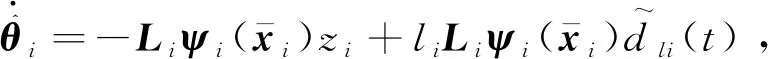
(19)
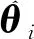
Stepn设计实际控制输入u。
定义xn的误差信号为zn=xn-αn-1,关于时间的导数为
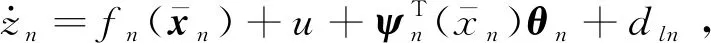
(20)

(21)
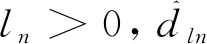
设计如下实际控制输入
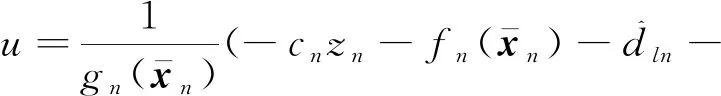
(22)
θn的自适应律为
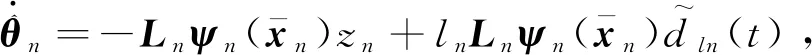
(23)
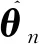
注3: 文献[26]先采用误差变换,再进行预定性能控制器设计,本文无须进行误差变换,只需在第一步构造障碍Lyapunov函数,减少了控制器设计的复杂程度。文献[27]也是通过在第一步设计时,构造障碍Lyapunov函数保证预定性能,但本文不仅考虑了预定性能控制问题,同时考虑了未知参数、外界干扰和执行器故障的综合影响。
注4: 文献[25]中障碍Lyapunov函数的形式为
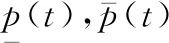
3 稳定性分析
本章基于Lyapunov稳定性理论对闭环系统的稳定性进行分析,可总结为如下定理形式。
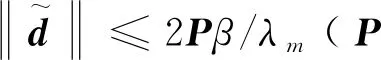
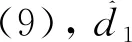

(24)
由式(24)可得
(25)
同理可得
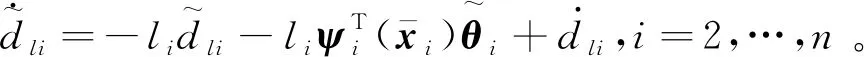
(26)
(27)

只要选择合适的参数l1,l2,…,ln,那么存在正定阵P使得DTP+PD=-Q,对于正定阵Q,λm是它的最小特征值。
选择如下Lyapunov函数
V=V1+V2+…+Vn+Vd,
(28)
式中,
(29)
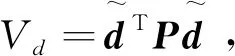
(30)
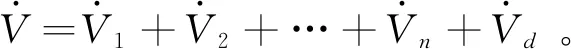
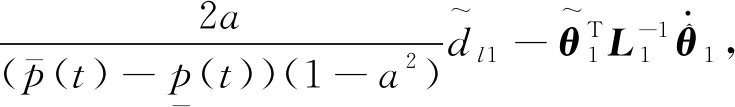
(31)
V2关于时间的导数为

(32)
将式(14)代入式(32)

(33)
Vi关于时间的导数为
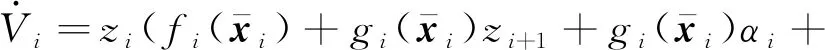
(34)
将式(18)代入式(34),则
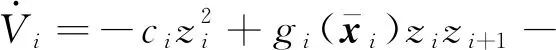
(35)
Vn关于时间的导数为
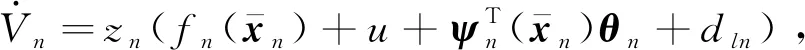
(36)
将式(22)代入式(36)得
(37)
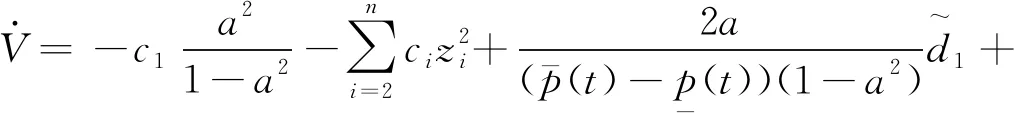
≤
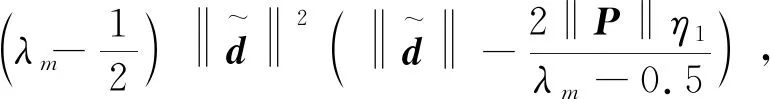
(38)

所以由引理1,式(38)满足
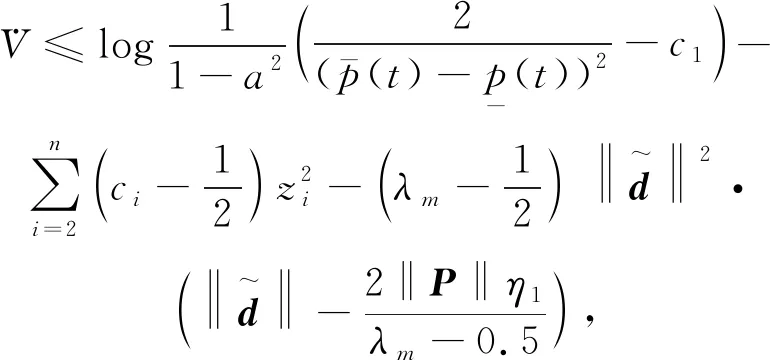
(39)
由上式,只要
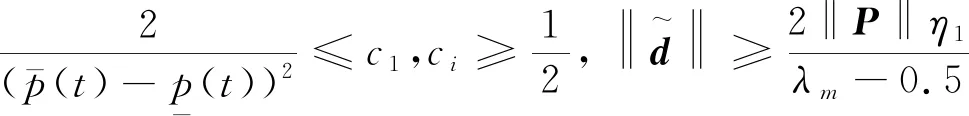
4 仿真分析
针对具有未知参数、外界干扰与执行器故障的永磁同步电机系统,采用前文所设计的控制策略,通过MATLAB R2010a/Simulink进行仿真,实现永磁同步电机系统角速度的稳定跟踪控制。
永磁同步电机的数学模型为
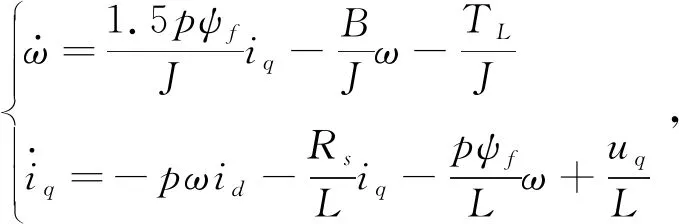
(40)
(41)
式中,id、iq分别为d轴和q轴的定子电流;ud、uq分别为d轴和q轴的定子电压;ω表示转子角速度;Rs为定子电阻,L为定子绕组等效电感;ψf为永磁体磁链;B是摩擦系数;p是极对数;J是转动惯量;TL为负载扰动。永磁同步电机参数为RS=0.14 Ω,L=4.6 mH,ψf=0.96 Wb,B=0.004,p=3,J=0.054 7 kg·m2。干扰观测器参数为a1=100,l1=l2=l3=50a1,控制器参数为c1=500,c2=180,c3=130,自适应律参数为L=0.1。
为方便控制器的设计,将式(40)和式(41)重写为如下形式:
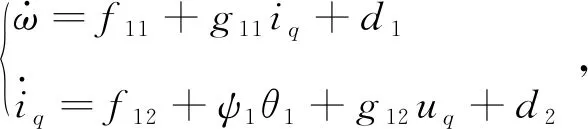
(42)
(43)
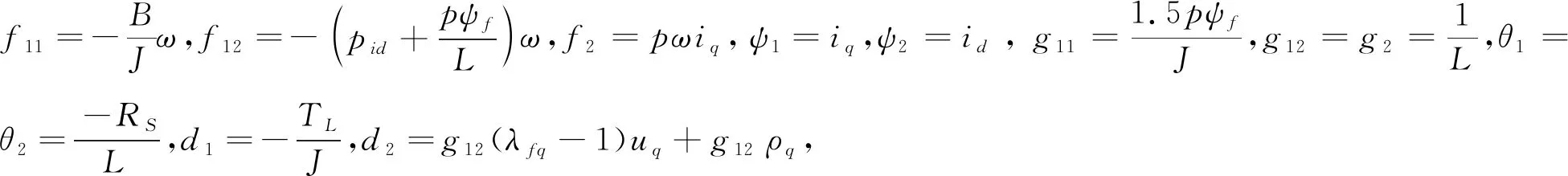
d3=g2(λfd-1)ud+g2ρd。
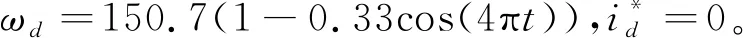

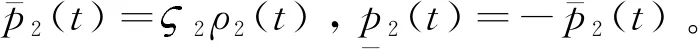
为更好地体现所设计的控制策略的优越性,考虑如下两种情形的仿真:情形1(Case1):考虑不确定参数、外界干扰、故障和输出误差约束。情形2(Case2):考虑不确定参数、外界干扰、故障。两种情形下的仿真结果如图1~图4所示。
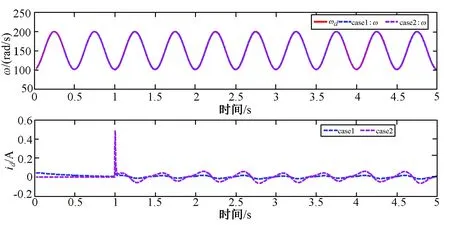
图1 角速度与电流的跟踪曲线Fig.1 Tracking curves of ω,id
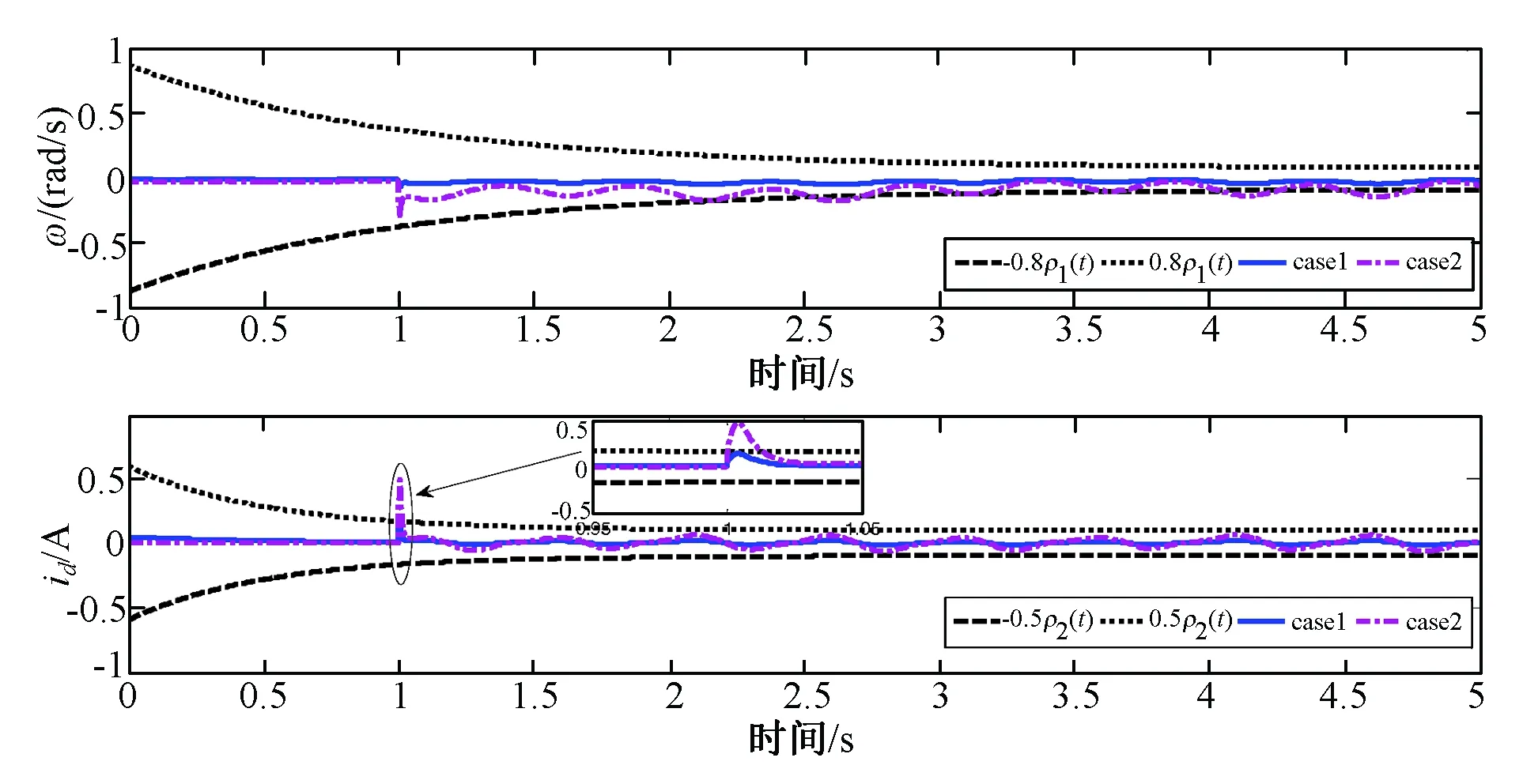
图2 跟踪误差曲线Fig.2 Curves of tracking error
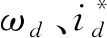
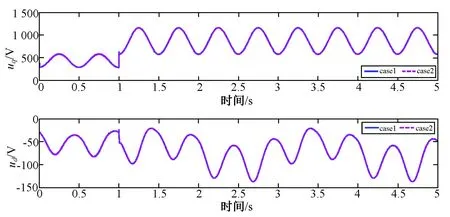
图3 控制输入曲线Fig.3 Curves of control inputs
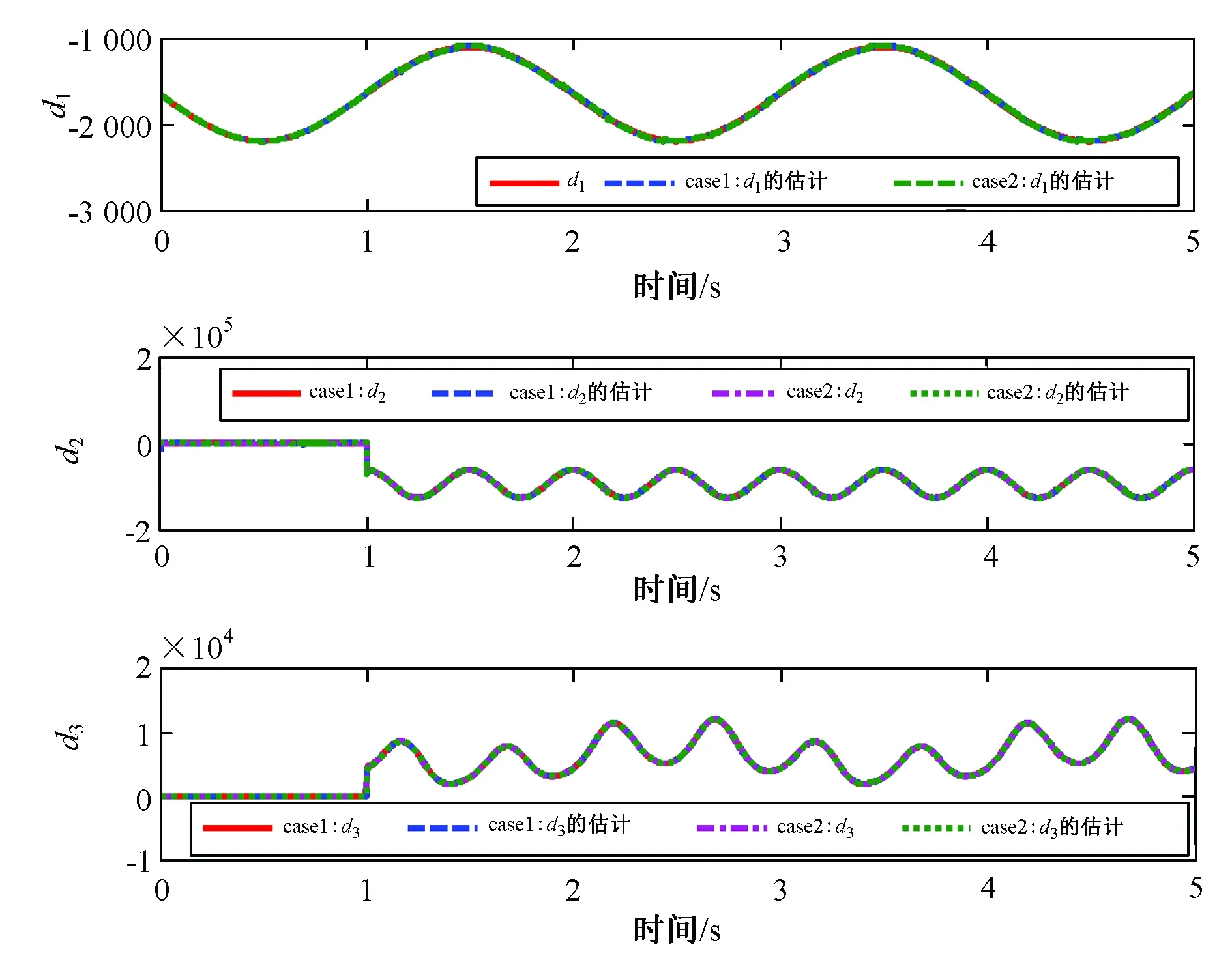
图4 综合不确定的估计曲线Fig.4 Curves of lumped uncertainty estimate
5 结论
本文考虑外界干扰、不确定参数和执行器故障影响下,非线性系统的预定性能控制问题,结合形式简单的障碍Lyapunov函数、干扰观测器与反步控制, 设计了自适应预定性能反步控制器。采用干扰观测器实现了综合不确定的估计,解决了传统反步控制的“计算爆炸”问题和执行器故障问题。通过稳定性分析表明所设计的控制策略,实现了输出误差的预定性能,进一步由仿真结果验证了本文所设计的控制器同时能够满足瞬态性能和稳态性能的要求。本文的理论结果还可以应用到飞行器系统、机器人系统。对于实际工程系统,状态变量以及输入约束也是需要考虑的问题,也是我们将关注的研究主题。
