传递函数辨识(19)：有限脉冲响应滑动平均系统的递阶递推增广参数估计

丁 锋,刘喜梅

(1．江南大学物联网工程学院，江苏 无锡214122;2．青岛科技大学 自动化与电子工程学院，山东 青岛266061)

在连载论文中，使用多新息辨识理论、递阶辨识原理、耦合辨识概念[1-6]，先后研究了信号模型、传递函数的参数估计[7-11]。最近，针对输出误差模型描述的动态随机系统:

研究了辅助模型(多新息)随机梯度算法、辅助模型(多新息)递推梯度算法、辅助模型(多新息)最小二乘算法等[12]，以及辅助模型递阶(多新息)梯度迭代算法、辅助模型递阶(多新息)最小二乘迭代算法等[13]。

有限脉冲响应滑动平均模型(finite impulse response moving average model，FIR-MA模型)也称为受控滑动平均模型(controlled moving average model，CMA模型)，它是一类特殊的方程误差滑动平均模型。滑动平均噪声干扰下的系统辨识方法称为增广辨识方法。

本研究针对有限脉冲响应滑动平均(FIR-MA)系统，通过辨识模型分解，研究递阶增广随机梯度(HESG)算法、递阶多新息增广随机梯度(HMIESG)算法、递阶增广梯度(HEG)算法、递阶多新息增广梯度(HMI-EG)算法、递阶增广最小二乘(HELS)算法、递阶多新息增广最小二乘(HMIELS)算法等。文献[14]提出了CMA系统的交互随机梯度辨识算法。本研究提出的递阶辨识方法可以推广用于其他线性和非线性随机系统，以及信号模型的参数辨识[15-25]。

1 有限脉冲响应滑动平均系统

有限脉冲响应滑动平均模型描述的系统称为有限脉冲响应滑动平均系统，受控滑动平均模型描述的系统称为受控滑动平均系统，余同。

考虑下列有限脉冲响应滑动平均模型(FIRMA模型)描述的随机控制系统，

其中{u(t)}和{y(t)}分别是系统的输入和输出序列，{v(t)}是零均值不可测白噪声序列，B(z)和D(z)是后移算子z－1的多项式(z－1y(t)＝y(t－1)或zy(t)＝y(t＋1)，且

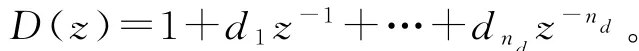
定义参数向量和信息向量:

注意到输入信息向量φ(t)包含了系统输入u(t－i)，是已知的;噪声信息向量ψ(t)包含了不可测噪声项v(t－i)，是未知的。

定义不可测滑动平均干扰噪声:

假设阶次n b和n d已知，记n＝n b＋n d。设t≤0时，各变量的初值为零:u(t)＝0，y(t)＝0，w(t)＝0，v(t)＝0。由式(5)和(2)可以写为

定义虚拟输出变量

由式(8)可得

式(9)、(6)是FIR-MA系统(2)的基于辨识模型分解得到的两个子辨识模型(sub-identification model)，即递阶辨识模型。它们可以看作两个子系统，一个包含了系统模型的参数向量b，一个包含了噪声模型的参数向量d。辨识模型式(8)分解为子辨识模型式(9)、(6)的递阶结构如图1所示。由于分解，导致两个子辨识模型间存在耦合变量(关联项)b和d。因此在推导两个子辨识算法时，需要根据递阶辨识原理，协调它们间的关联项。基于分解的辨识方法也称为递阶辨识方法。

图1 辨识模型分解为子辨识模型的梯阶结构Fig．1 Hierarchical structure of decomposing the identification model

2 递阶增广随机梯度辨识算法

对于FIR-MA系统的递阶辨识模型式(9)和式(6)，定义两个梯度准则函数(gradient criterion function):

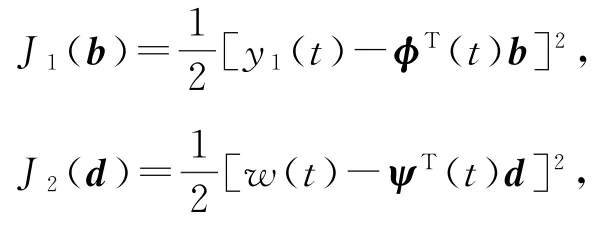
然而，算法式(10)～(13)不可实现，因为右边包含了未知信息向量ψ(t)，参数向量b和d，这里解决方法是应用递阶辨识原理，细节如下。

从式(8)可得

上式中未知的ψ(t)，b和d分别用其估计和代替，则v(t)的估计(即残差)可由式(15)计算:

式(10)～(13)中未知ψ(t)，d和b分别用其估计和代替，得到式(16)～(19)，联立式(3)，(14)～(15)，便得到辨识FIR-MA系统参数向量b和d的递阶增广随机梯度算法(hierarchical extended stochatic gradient algorithm，HESG算法):

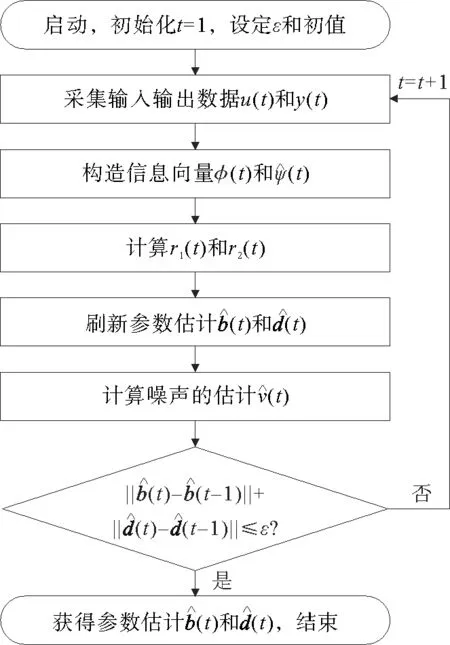
图2 递阶增广随机梯度(HESG)算法计算流程Fig．2 Flowchart of the HESG algorithm

1)初始化:令t＝1。置初值(0)＝1nb/p0，(0)＝1n d/p0，r1(0)＝1，r2(0)＝1，u(t－i)＝0，(t－i)＝1/p0，i＝1，2，…，max[n b，n d]，p0＝106。给定参数估计精度ε。

2)采集输入输出数据u(t)和y(t)。用式(21)构造信息向量φ(t)，用式(22)构造噪声信息向量(t)。

3)用式(17)计算r1(t)，用式(19)计算r2(t)。

注1对于HESG算法式(16)～(24)，如果取式(16)中的r1(t)与式(18)中的r2(t)相等，且都为

r(t)＝r(t－1)＋，r(0)＝1，

那么HESG算法就退化为ESG算法。

式(16)～(24)是基于残差的HESG算法，下面是基于新息的HESG算法:

3 递阶多新息增广随机梯度算法

设正整数p表示新息长度。基于多新息辨识理论[16]和HESG辨识算法(16)～(24)，将系统输出y(t)，信息向量φ(t)和扩展为堆积输出向量Y(p，t)，堆积信息矩阵Φ(p，t)和:

将式(16)和式(18)中标量新息(scalar innovation)

扩展为新息向量(innovation vector)

注意到Y(1，t)＝y(t)，E(1，t)＝e(t)，Φ(1，t)＝φ(t)，式(16)和式(18)可以等价表达为

这是新息长度p＝1的两阶段“多新息”随机梯度算法。将两式中Φ(1，t)和E(1，t)里的1换为p，得到式(38)和式(41)，联立式(34)～(37)，(17)和(19)～(24)，便得到辨识FIR-MA系统参数向量b和d的递阶多新息增广随机梯度算法(hierarchical multi-innovation extended stochastic gradient algorithm，HMI-ESG算法):

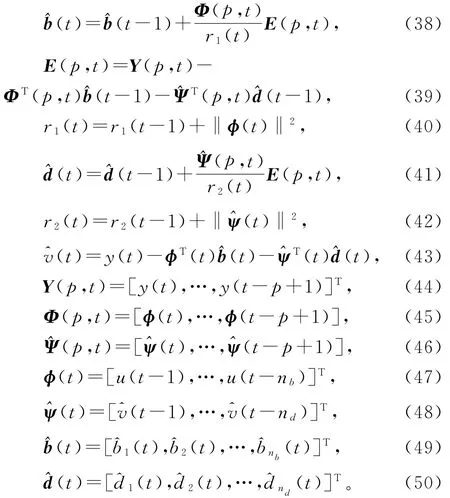
当新息长度p＝1时，HMI-ESG算法退化为HESG算法(16)～(24)。

1)初始化:令t＝1，给定新息长度p和参数估计精度ε。置初值/p0，r1(0)＝1，r2(0)＝1，y(t－i)＝0，u(t－i)＝0，(t－i)＝1/p0，i＝1，2，…，p＋max[n b，n d]，p0＝106。

2)采集输入输出数据u(t)和y(t)。用式(47)和(48)构造信息向量φ(t)和(t)，用式(44)～(46)构造堆积输出向量Y(p，t)，堆积信息矩阵Φ(p，t)和(p，t)。

3)用式(39)计算新息向量E(p，t)，用式(40)计算r1(t)。

5)用式(42)计算r2(t)，根据式(41)刷新参数估计向量(t)。用式(43)计算残差(t)。

式(38)～(50)是基于残差的HMI-ESG算法，下面是辨识FIR-MA系统参数向量b和d的基于新息的HMI-ESG算法:

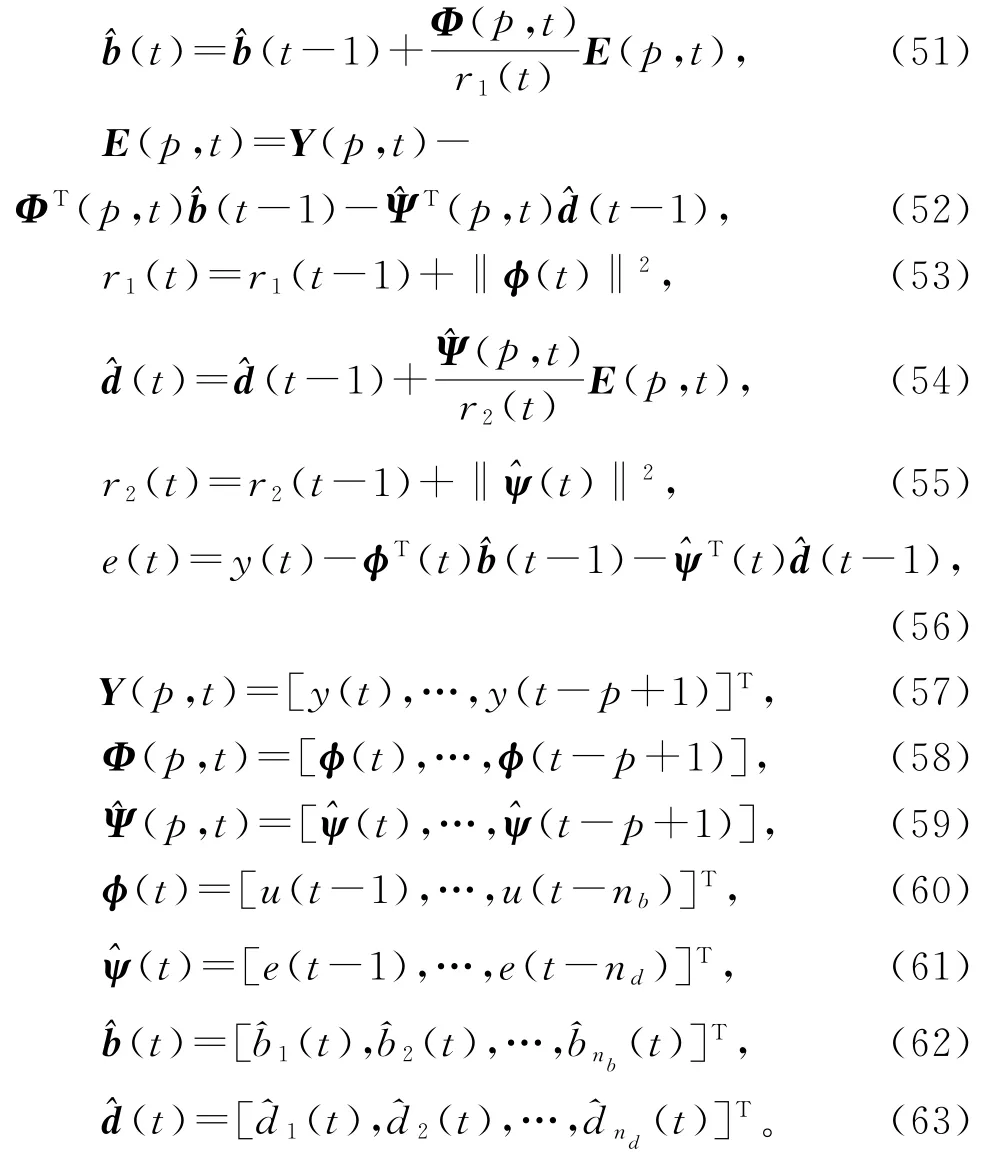
随机梯度算法(包括多新息随机梯度算法、递阶随机梯度算法、递阶增广随机梯度算法)的收敛速度很慢，为改善随机梯度类算法的性能，可以引入收敛指数、遗忘因子等提高算法的性能。

在HMI-ESG算法中引入收敛指数、遗忘因子等，得到对应的修正递阶多新息随机梯度(M-HMIESG)算法、遗忘因子递阶多新息随机梯度(FF-2SMISG)算法、遗忘因子修正递阶多新息随机梯度(FF-M-HMI-ESG)算法等。

4 递阶递推增广梯度辨识算法

对于FIR-MA系统的递阶辨识模型式(9)和式(6)，定义准则函数:

定义堆积输出向量Y(t)，堆积信息矩阵Φ(t)，堆积虚拟输出向量Y1(t)，堆积噪声向量W(t)和堆积噪声矩阵Ψ(t)如下:

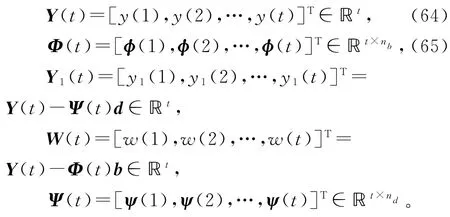
准则函数J3(b)和J4(d)可等价表示为

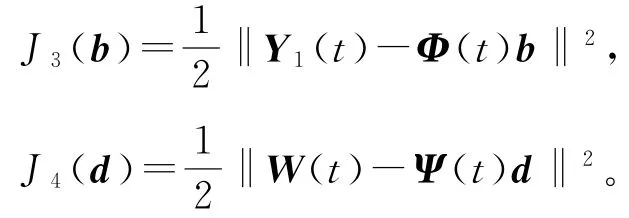
分别求准则函数J3(b)和J4(d)对参数向量b和d的梯度，得到

定义递推关系:

于是，梯度可以表示为

关系式(70)～(77)不可实现，因为右边包含了未知信息向量ψ(t)，d和b。解决的办法是用它们的估计(t)(t－1)和(t－1)代替，联立式(20)～(24)，便得到辨识FIR-MA系统参数向量b和d的递阶增广梯度算法(hierarchical extended gradient algorithm，HEG算法):

这是基于残差的HEG算法。将算法(78)～(90)中的式(86)和式(88)修改为就得到基于新息的HEG算法。

图3 递阶增广梯度(HEG)算法计算流程Fig．3 Flowchart of the HEG algorithm

1)初始化:取μ＝1，给定ε。令t＝1，置初值1/p0，i＝1，2，…，max[n b，n d]，p0＞0是一个大常数，如p0＝106。

2)采集输入输出数据u(t)和y(t)。用式(87)构造信息向量φ(t)，用式(88)构造信息向量(t)。

3)用式(79)计算r1(t)，用式(80)计算向量ξ1(t)，用式(81)计算矩阵R1(t)。用式(78)刷新参数估计向量(t)。

4)用式(83)计算r2(t)，用式(84)计算向量，用式(85)计算矩阵R2(t)。用式(82)刷新参数估计向量(t)。用式(86)计算残差(t)。

5 递阶多新息增广梯度辨识算法

设正整数p表示新息长度。对于FIR-MA系统的递阶辨识模型(9)和(6)，利用从t－p＋1到t的最新p组数据，定义堆积输出向量Y(p，t)和Y1(p，t)，堆积噪声向量W(p，t)，堆积信息矩阵Φ(p，t)和信息矩阵Ψ(p，t)如下:

定义两个多新息准则函数:

定义堆积输出信息向量Zi，t和堆积信息矩阵Ωi，t如下:

则准则函数J5(b)和J6(d)可以写为

求准则函数J5(b)和J6(d)分别对参数向量b和d的一阶偏导数，可以得到两个准则函数的梯度向量:

其中

设μ1(t)≥0和μ2(t)≥0为收敛因子。根据负梯度搜索，极小化准则函数J5(b)和J6(d)，可以得到下列梯度递推关系:

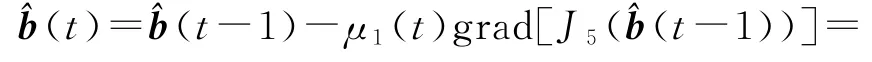
由于特征值计算很复杂，故收敛因子也可简单取为

据此可取μi(t)＝1/r i(t)，r i(0)＝1，i＝1，2，且

由于式(95)～(102)右边存在未知量Ψ(p，t)，ψ(t)，d和b，所以无法计算参数估计(t)和(t)，解决的办法是应用递阶辨识原理，那些未知量用其估计和(t－1)代替，联立式(44)～(50)，便得到辨识FIR-MA系统参数向量b和d的递阶多新息增广梯度算法(hierarchical multi-innovation extended gradient algorithm，HMI-EG算法):

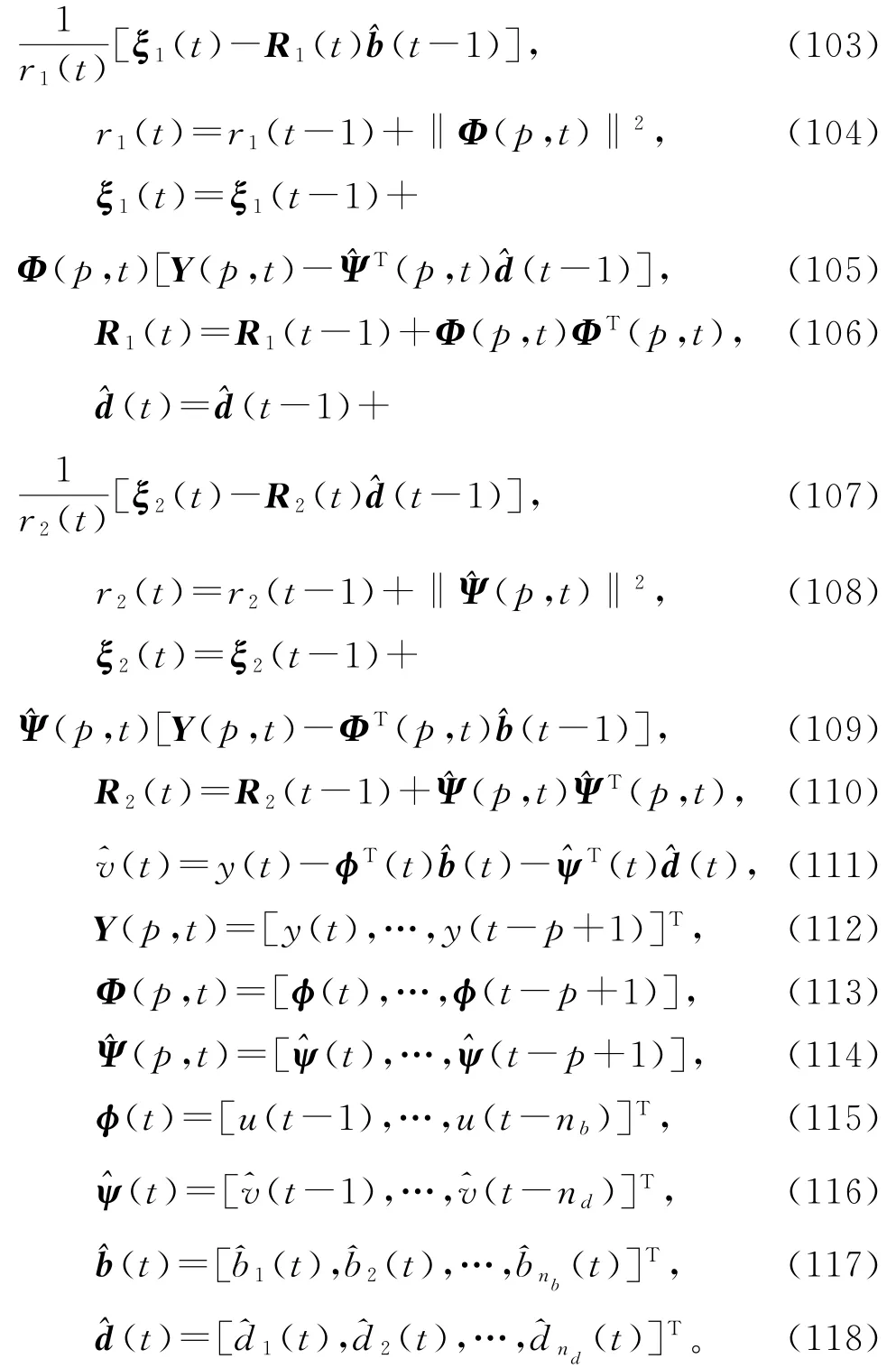
这是基于残差的HMI-EG算法。将算法(103)～(118)中的式(111)和式(116)修改为

就得到基于新息的HMI-EG算法。

1)初始化:给定新息长度p和参数估计精度ε。令t＝1，置初值max[n b，n d]，p0＞0是一个大常数，如p0＝106。

2)采集输入输出数据u(t)和y(t)。用式(115)构造信息向量φ(t)，用式(116)构造信息向量(t)。用式(112)～(114)构造堆积输出向量Y(p，t)，堆积信息矩阵Φ(p，t)和(p，t)。

3)用式(104)计算r1(t)，用式(105)计算向量ξ1(t)，用式(106)计算矩阵R1(t)。用式(103)刷新参数估计向量(t)。

4)用式(108)计算r2(t)，用式(109)计算向量ξ2(t)，用式(110)计算矩阵R2(t)。用式(107)刷新参数估计向量(t)。用式(111)计算残差(t)。

在HMI-EG算法(103)～(118)中引入加权因子(加权矩阵)、遗忘因子，便得到加权递阶多新息增广梯度(W-HMI-EG)算法、遗忘因子递阶多新息增广梯度(FF-HMI-EG)算法、加权遗忘因子递阶多新息增广梯度(W-FF-HMI-EG)算法。

6 递阶增广最小二乘辨识算法

参考递推最小二乘算法的推导，极小化准则函数J3(b)和J4(d)，可得到以下最小二乘递推关系:

然而，同一个问题出现:算法(121)～(129)不可实现，因为右边包含了未知信息向量ψ(t)，参数向量d和b。解决的办法是用它们的估计(t)(t－1)和(t－1)代替，得到式(130)～(135)，联立式(20)～(24)，便得到辨识FIR-MA系统参数向量b和d的递阶增广最小二乘算法(hierarchical extended least squares algorithm，HELS算法):

这个算法也称为基于残差的HELS算法，读者可研究它的收敛性[3]。下面给出辨识FIR-MA系统参数向量b和d的基于新息的递阶增广最小二乘算法(HELS算法):

图4 递阶增广最小二乘(HELS)算法计算流程Fig．4 Flowchart of the HELS algorithm

1)初始化:令t＝1。置初值max[n b，n d]，p0＝106。给定精度ε。

2)采集输入输出数据u(t)和y(t)。用式(137)构造信息向量φ(t)，用式(138)构造噪声信息向量(t)。

3)用式(131)和式(134)计算增益向量L1(t)和L2(t)，用式(132)和式(135)计算协方差阵P1(t)和P2(t)。

7 递阶多新息增广最小二乘算法

设p为新息长度。根据多新息辨识理论，基于HELS算法(130)～(140)，将输出y(t)，信息向量φ(t)和(t)扩展为堆积输出向量Y(p，t)，堆积信息矩阵Φ(p，t)和(p，t):

将式(130)和式(133)中标量新息(scalar innovation)

扩展为新息向量

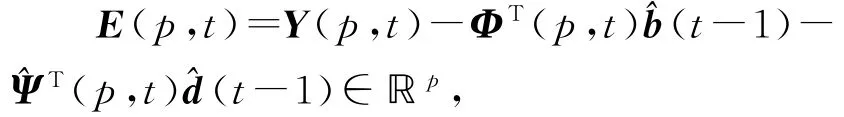
便得到辨识FIR-MA系统参数向量b和d的递阶多新息增广最小二乘算法(hierarchical multi-innovation extended least squares algorithm，HMI-ELS算法):

HMI-ELS算法(152)～(166)计算参数估计向量(t)和(t)的步骤如下。

1)初始化:给定新息长度p和估计精度ε。令t＝1。置初值

2)采集输入输出数据u(t)和y(t)。用式(163)构造信息向量φ(t)，用式(164)构造噪声信息向量(t)。用式(160)～(162)构造堆积输出向量Y(p，t)，堆积信息矩阵Φ(p，t)和(p，t)。

3)用式(153)计算新息向量E(p，t)，用式(154)和式(157)计算增益向量L1(t)和L2(t)，用式(155)和(158)计算协方差阵P1(t)和P2(t)。

式(152)～(166)是基于残差的HMI-ELS算法，下面是辨识FIR-MA系统参数向量b和d的基于新息的递阶多新息增广最小二乘算法(HMI-ELS算法):

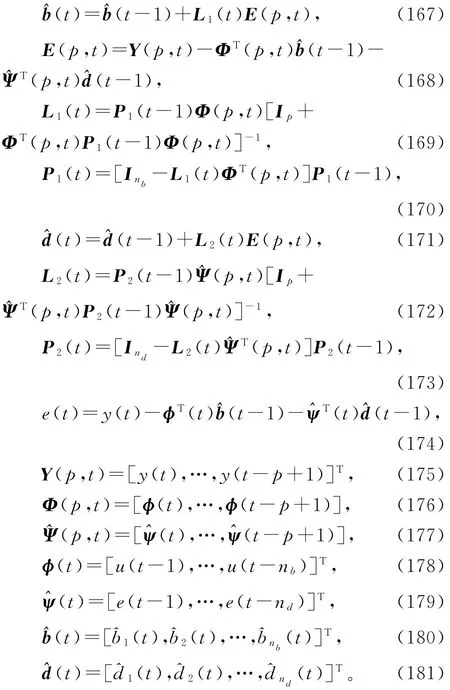
8 结 语

针对最简单的有色噪声干扰的有限脉冲响应滑动平均模型，利用系统的观测输入输出数据，基于递阶辨识原理，对辨识模型进行分解，得到两个递阶辨识子模型，一个包含系统模型的参数，一个包含噪声模型的参数，推导出递阶增广随机梯度辨识算法和递阶多新息增广随机梯度辨识算法，递阶增广梯度辨识算法和递阶多新息增广梯度辨识算法，以及递阶增广最小二乘辨识算法和递阶多新息增广最小二乘辨识算法等。提出的分解辨识思想可以推广到大规模线性随机系统和复杂非线性随机系统的辨识，其干扰可以是有色噪声。