基于CEEMDAN-Hilbert-CNN的滚动轴承故障诊断

李雪颖,朱哈娜,刘慧明

(青岛科技大学自动化与电子工程学院，山东 青岛266061)

滚动轴承是旋转机械中应用最多但最易损坏的机器零件，其工作好坏直接影响机械的工作状态。滚动轴承故障如果不能及时准确地诊断，将会造成财产损失，人员伤亡等一系列严重的问题。因此对滚动轴承振动信号中的特征成分实现精确提取以及对故障特征的准确分类是十分重要的[1]。近些年时频分析、机器学习及深度学习被广泛应用于故障诊断[2-6]。1998年，HUANG等[7]提出了希尔伯特黄变换(Hilbert-Huang transform，H HT)。希尔伯特黄变换在处理非线性、非平稳信号方面具有很大的优越性，因而在故障诊断方面得到广泛应用。HHT包括经验模态分解(empirical mode decomposition，EMD)和希尔伯特变换(Hilbert transform)两部分。尽管H HT在处理非线性、非稳定信号方面存在很大的优越性，但由于H HT存在模态混叠和端点效应等诸多问题，易导致特征提取不准确。为克服模态混叠的问题，HUANG等[8-10]基于白噪声的统计特性引入了总体经验模态分解(ensemble empirical mode decomposition，EEMD)，但是由于引入的白噪声不能完全被消除易造成重构误差不具有完备性且计算量也比较大。为了抑制模态混叠排除白噪声的干扰，2010年，HUANG等[11]提出向信号中添加2个相反的白噪声的互补集合经验模态分解(complementary ensemble empirical mode decomposition，CEEMD)，CEEMD方法消除了EEMD分解中添加白噪声的影响，但是计算量变得更大。2011年，TORRES等[12]提出了一种自适应噪声的完备经验模态分解(complete ensemble empirical mode decomposition with adaptive noise，CEEMDAN)，与EEMD和CEEMD方法相比较，CEEMDAN不仅提高了分解的效果，改善了分解的完备性，还大大减少了计算量。2016年，GUO等[13]提出了一种自适应深卷积神经网络进行故障诊断。2019年，赵迎等[14]提出了提出基于深度学习的滚动轴承故障诊断，将包络谱作为输入数据，并改进了卷积神经网络。2019年，ZHANG等[15]提出二维码与卷积神经网络相结合的故障诊断方法。近年来，深度神经网络因其强大的特征学习能力和优异的复杂数据处理能力，而广泛应用于语音识别、图像识别和视频分类领域[16-17]，但应用于故障诊断方面的文献尚不多见。

基于以上考虑，本研究提出CEEMDAN-Hilbert-CNN方法，对故障信号进行分类。本研究采用的CEEMDAN不仅有效解决了EMD分解中存在的模态混叠问题，还去除了EEMD分解中因残留白噪声而存在的重构误差，具有良好的特征提取能力。采用的CNN具有稀疏交互和权值共享特性，在处理复杂的高维数据方面无压力，学习能力强，特征分类效果好。实验数据表明本研究提出的基于CEEMDAN-Hilbert-CNN的滚动轴承故障诊断新方法合理且行之有效。

1 基于CEEMDAN-Hilbert-CNN的滚动轴承故障诊断方法

基于CEEMDAN-Hilbert-CNN的滚动轴承故障诊断新方法首先将CEEMDAN和Hilbert结合得到的改进希尔伯特-黄变换，然后将改进的希尔伯特-黄变换与CNN结合。

1．1 EEMD方法

添加白噪声的EEMD方法在一定程度上解决了EMD存在的模态混叠问题。EEMD算法如下。

1)将原始信号x(t)添加正态分布的高斯白噪声ωi(t)(ωi(t)为第i次添加的白噪声，白噪声标准差一般为被测信号的0.1～0.4倍)，得到新的信号

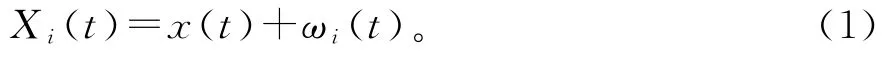
2)将加入白噪声的信号进行EMD分解(EMD分解流程图如图1所示)得到IMF分量IMFi(t)和残差r(t)，(i＝1，…，K)。

3)重复N次步骤1和2，每次加入新的正态分布高斯白噪声序列，X i(t)为第i次添加高斯白噪声后的信号，IMFij(t)为第i次添加高斯白噪声后分解的第j个IMF，(j＝1，…，K)，即

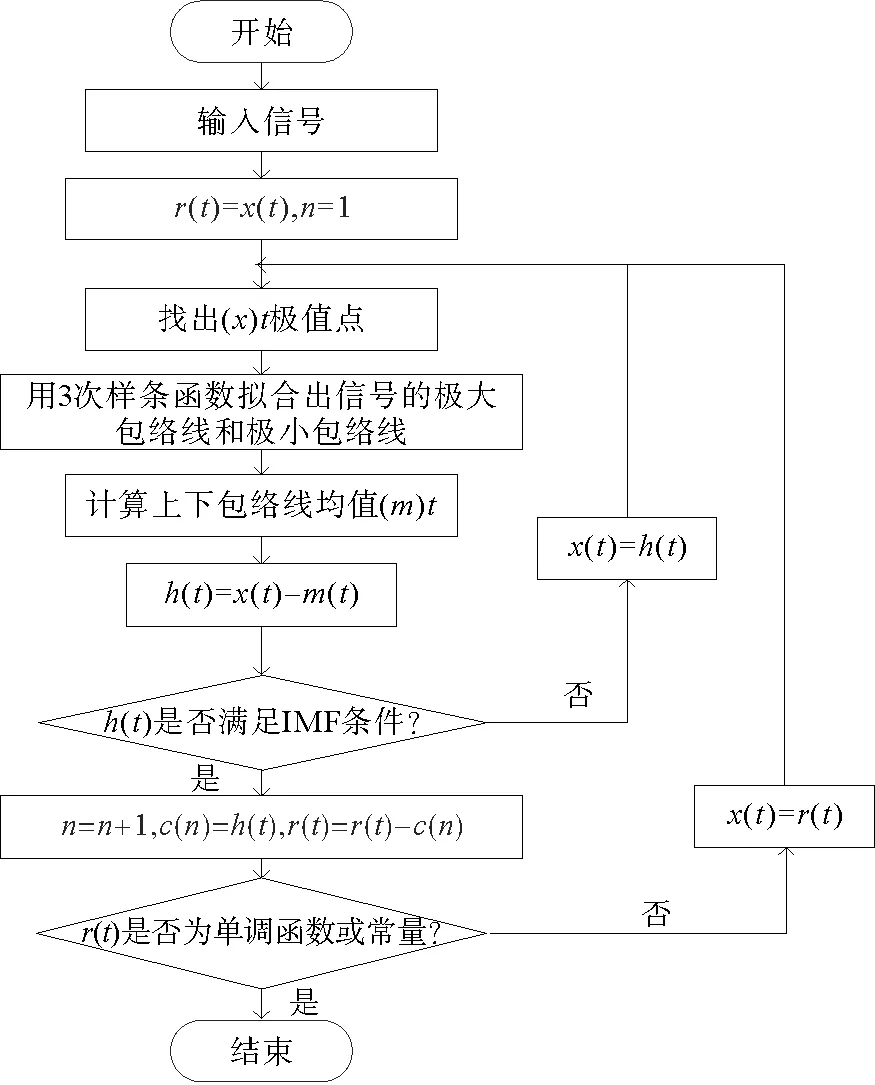
图1 经验模态分解方法流程Fig．1 Empirical mode decomposition method

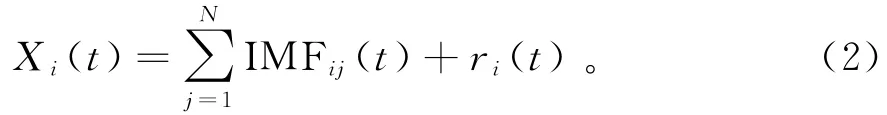
4)将每次得到的IMF进行总体平均计算，以消除多次添加高斯白噪声造成的干扰，最终得到的IMF分量为IMFj，IMFj为对原始信号进行EEMD分解后所得第j个IMF分量，余项表示为r(t)。原信号x(t)则可表示为

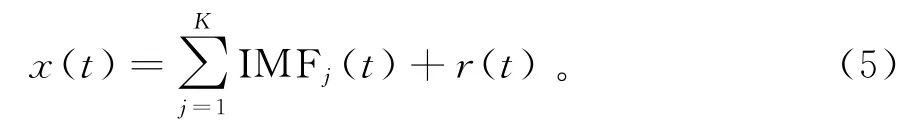
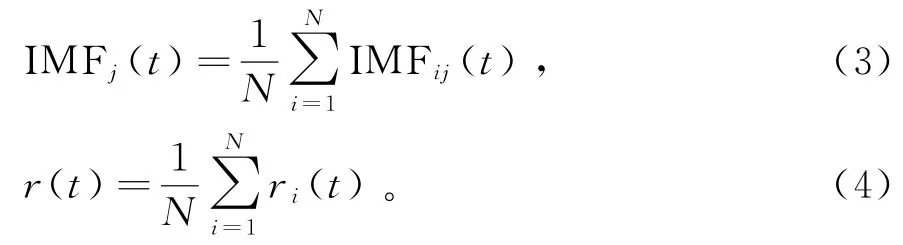
1．2 CEEMDAN算法

EEMD方法通过添加白噪声解决了模态混叠问题，但采用有限次取平均值的方法并不能完全消去另外添加的白噪声。EEMD分解中，由于每一个X j(t)都添加不同的白噪声且是独立分解的，因此每次得到的残差信号均不同[8]。为克服EEMD算法的不足，降低重构信号的失真率，CEEMDAN利用高斯白噪声频率均匀分布的统计特性，通过向原始信号附加自适应髙斯白噪声来计算唯一的残差信号获取IMF(t)。CEEMDAN算法具体如下。

1)利用EEMD算法得到第一个固有模态函数IMF1(t)，

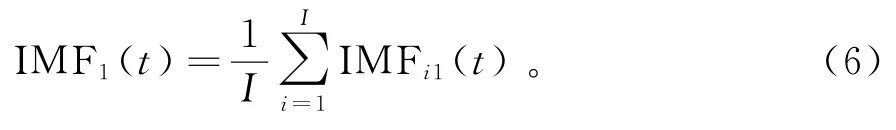
2)在第一阶段得到第一个余量r1(t)，

3)对信号r1(t)＋ε1E1(ωi(t))(i＝1，2，…，I)进行分解，直到得到第一个EMD固有模态函数为止，再计算第二个固有模态函数，

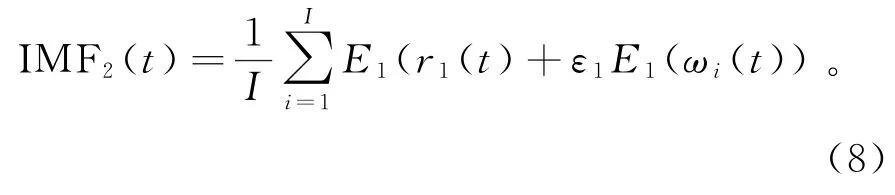
其中，定义算子E j(·)是通过EMD分解所获得的第j个固有模态函数。通过CEEMDAN分解所获得的第j个固有模态函数记作IMFj(t)，ωi(t)为满足N(0，1)的白噪声。

4)对于j＝2，…，J，计算第j个余量r j(t)，

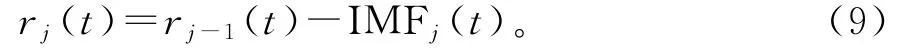
5)对第j个信号r j(t)＋εjE j(ωi(t))进行分解，同步骤3)计算过程一样，第j＋1个固有模态函数IMFj＋1(t)可以表示为

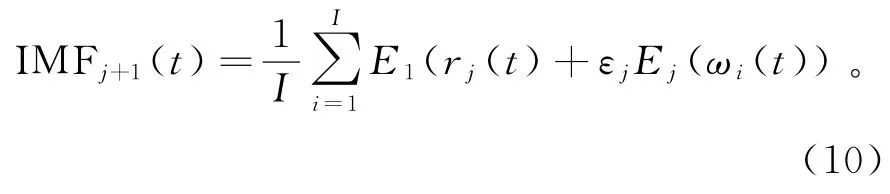
6)返回步骤4)并重复步骤4)～6)直至剩余残差信号不能再分解，其剩余残差信号R(t)满足关系

因此，初始信号被分解后可以表示为

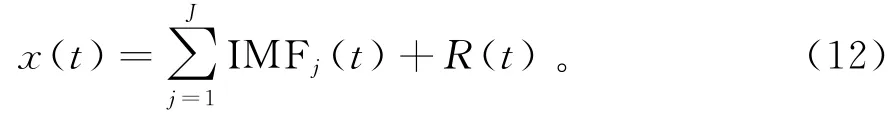
1．3 Hilbert算法

对CEEMDAN分解的IMF分量进行Hilbert变换，具体算法如下。

1)对于任意时间序列x(t)进行Hilbert变换都有y(t)，即

ρ为广义积分的柯西主量。

2)解析函数Z(t)即可表示为

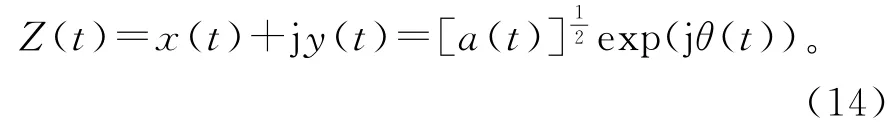
3)幅值函数α(t)表示为

4)相位函数θ(t)即

5)瞬时频率ω(t)可求得

所有的IMF分量经希尔伯特变换后得到希尔伯特频谱。

1．4 卷积神经网络

典型的卷积神经网络(CNN)的基本结构主要由卷积层和池化层交替连接构成。完整的卷积神经网络则还需要输入层、输出层以及输出层前面的全连接层。本研究使用CNN进行故障特征学习的过程为如图2所示。

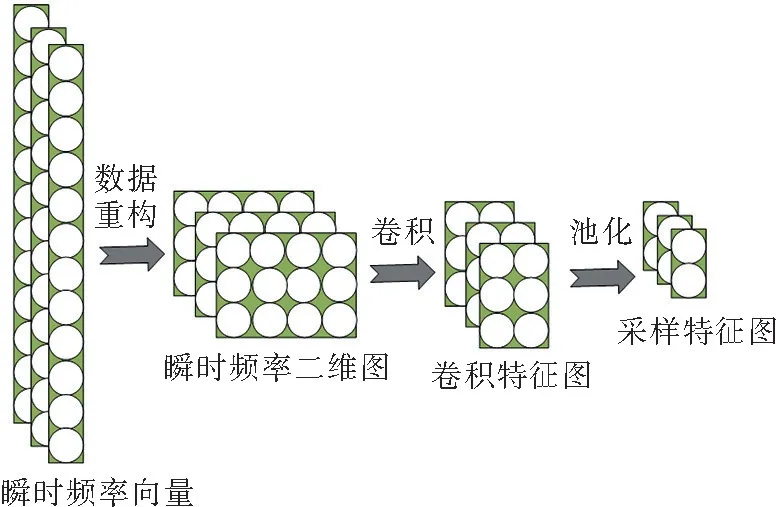
图2 CNN对数据故障数据的特征学习过程Fig．2 CNN′s feature learning process of data fault data

1．4．1 卷积层

卷积的作用是进行特征提取。卷积运算通过3个重要的思想来改进机器学习系统:稀疏交互(sparse interactions)、权值共享(weight sharing)、等变表示(equivariant representations)[18]。稀疏交互:在与输入层连接的每个神经元仅与输入神经元的一块区域部分连接，如图3所示。与传统的全连接神经网络相比大量减少了训练参数，加快了学习速率。权值共享:计算同一个深度切片的神经元时采用的滤波器是共享的，因此在很大程度上减少了参数，如图3所示。等变表示:也称为平移等变，由于权值共享的特殊性质使卷积神经网络具有平移等变特性。如果一个函数具有输入变化，输出也以同样的方式改变这一性质，则这一函数就是等变得。

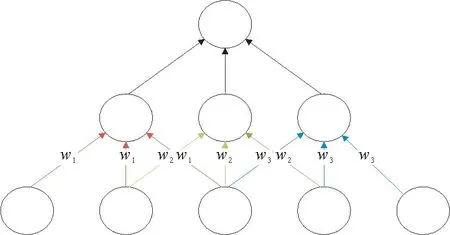
图3 稀疏交互和权值共享Fig．3 Sparse interactionsandweight sharing

1．4．2 池化层

池化层也叫子采样层，池化层位于卷积层后面，池化操作目的是对卷积层输出的特征图进行降维，常用的池化操作有最大池化和平均池化。最大池化和平均池化如图4所示。

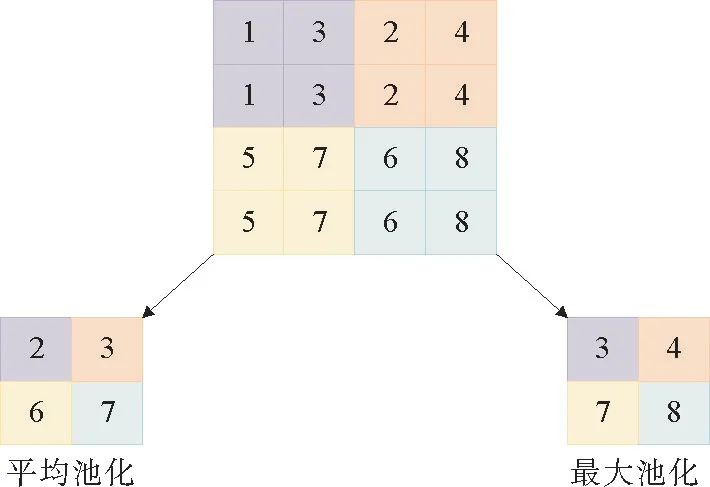
图4 平均池化和最大池化Fig．4 Average poling and max pooling

1．5 基于CEEMDAN-Hilbert-CNN滚动轴承故障诊断流程设计

基于CEEMDAN-Hilbert-CNN滚动轴承故障诊断流程图如图5所示。

图5 滚动轴承故障诊断流程Fig．5 Rolling bearing fault diagnosis process

详细步骤如下。

1)将滚动轴承故障数据与正常情况下的原始振动数据进行CEEMDAN分解，得到若干IMF分量。

2)将IMF分量进行Hilbert变换，得到瞬时频率向量。

3)将瞬时频率向量进行数据重构，使得重构数据满足卷积神经网络输入条件。

4)将重构的故障数据输入卷积神经网络进行故障分类。

2 实验结果与讨论

2．1 实验数据介绍

本研究采用在滚动轴承故障诊断中广泛应用的美国凯斯西储大学(Case Western Reserve University)轴承数据中心网站的滚动轴承数据[19]进行实验。如图6所示，实验台由左边的2 hp电动机，中间的扭矩传感器以及右边的测力计和没在图中出现的控制电子设备组成。被测轴承型号为SKF6205-2RS JEM SKF，在故障直径0.007 in(1 in＝2．54 cm)，转速1 797 r·min－1，电机负载为0，采样频率12 k Hz的情况下，使用的实验数据共包括3组:正常基准数据、滚动体故障数据和外圈居中位置故障数据。

图6 滚动轴承故障诊断实验台Fig．6 Experimental station of rolling bearing fault diagnosis

2．2 数据分析及处理

3类振动数据时域波形如图7所示。

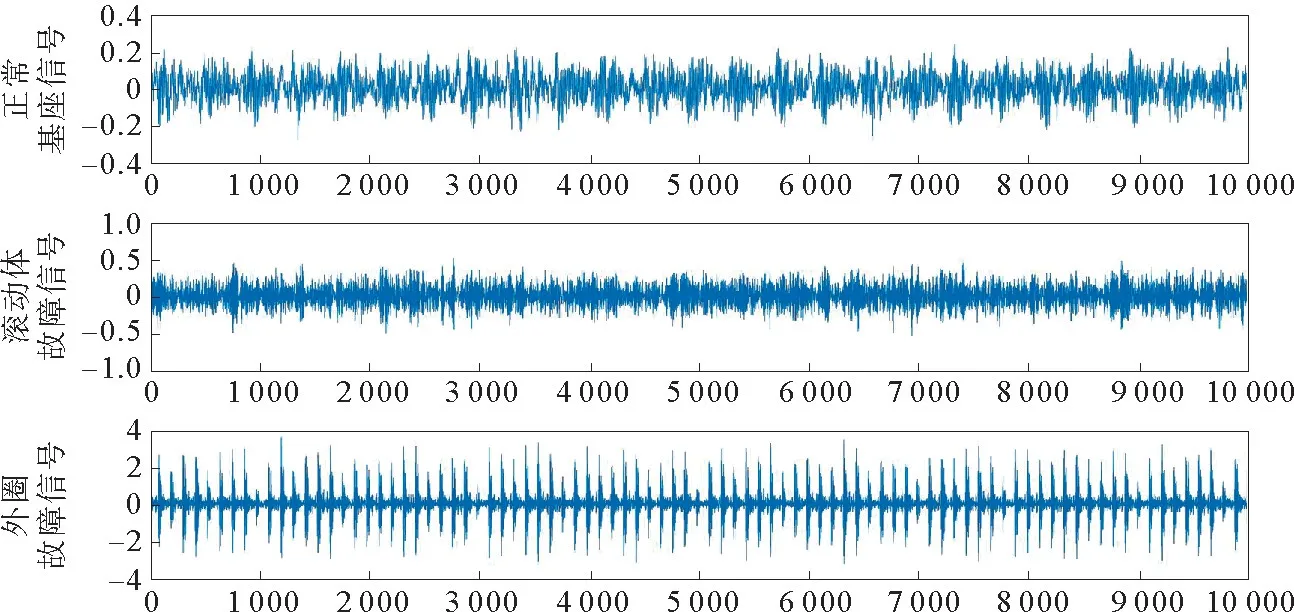
图7 原始信号波形图Fig．7 Original signal waveform

这3类信号单从波形上是很难区分是否为故障信号的，因此对原始信号采用CEEMDAN、EEMD和EMD分解，得到一系列从高频到低频率分布的IMF分量。图8、图9和图10别为滚动体故障信号被CEEMDAN、EEMD和EMD分解的前5个IMF分量。

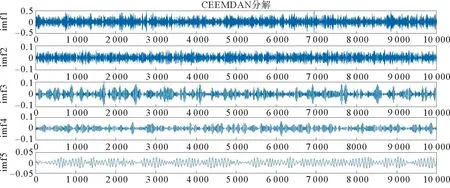
图8 CEEMDAN：滚动体故障信号前5个IMF分量Fig．8 CEEMDAN:First five IMF components of the ball fault signal

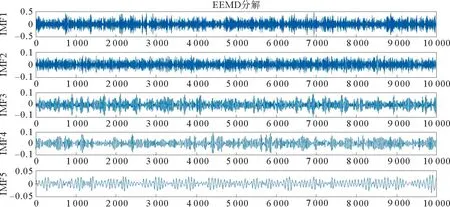
图9 EEMD：滚动体故障信号前5个IMF分量Fig．9 EEMD:First four IMF components of the ball fault signal

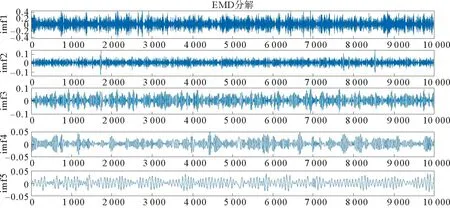
图10 EMD：滚动体故障信号前5个IMF分量Fig．10 EMD:First five IMF components of the ball fault signal

由图8、图9、图10可见，EMD分解的前5个分量明显存在波形重叠，EEMD与EMD相比，在一定程度上降低了波形重叠，CEEMDAN与EEMD和EMD相比明显很大程度改善了波形重叠问题。CEEMDAN极大地改善了模态混叠效应。

依据上述步骤分别对故障原始信号和正常原始信号进行EMD、EEMD和CEEMDAN分解，并进行Hilbert变换，即可得到包含两种数据信号的3种实验数据矩阵。并分别选取BP和卷积神经网络2个分类器进行分类比较。

2．3 故障分类结果及实验数据分析

依据本研究提出的CEEMDAN-Hilbert-CNN方法对基于真实工况数据的正常振动信号和2类故障振动信号进行分类，随机选取正常数据100 000个、滚动体故障数据100 000个、外圈故障数据100 000个作为训练集，正常数据20 000个、滚动体故障数据20 000个、外圈故障数据20 000个作为训练集，EMD-Hilbert-CNN选用与本研究提出方法参数相同的CNN进行诊断，CEEMDAN-Hilbert-BP和EEMD-Hilbert-BP选取与本研究提出方法故障特征相同的数据集输入BP进行分类，实验结果如表1所示。

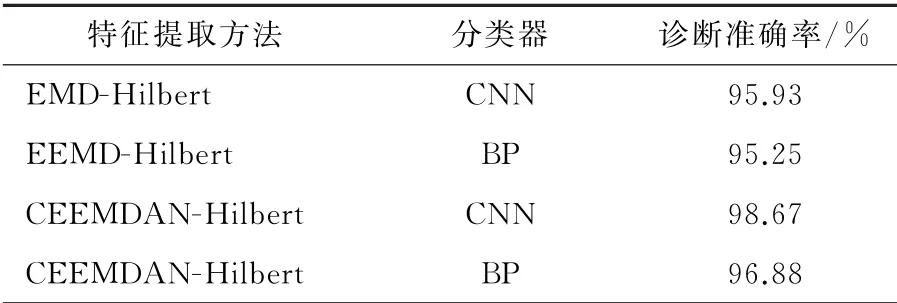
表1 不同特征提取及分类器效果比较Table 1 Effect comparison of different feature extraction method and classifier

由表1结果可以看出，本研究提出的基于CEEMDAN-Hilbert-CNN在滚动轴承故障诊断中，具有更准确的诊断率。在分类器均为CNN的情况下，使用特征提取方法EMD-Hilbert和CEEMDAN-Hilbert进行故障特征提取，故障诊断结果对比表明CEEMDAN相对于EMD能够更准确提取故障特征;在分类器均为BP的情况下，使用EEMD-Hilbert和CEEMDAN-Hilbert进行故障特征提取，故障诊断结果对比表明CEEMDAN相对于EEMD更能准确提取故障特征;在特征提取方法均为CEEMDAN-Hilbert情况下，使用分类器BP和CNN进行故障分类，故障诊断结果对比可得CNN相对于BP性能更加优越。

3 结 语

所提出的基于CEEMDAN-Hilbert-CNN的滚动轴承故障诊断方法，一方面由CEEMDAN取代EMD，提出改进的希尔伯特黄变换，实验表明抑制了信号分解造成的模态混叠，能够更好地提取故障特征;另一方面将CNN应用于故障诊断，改善了传统神经网络分类误差大，学习能力低的问题，提高了故障诊断分类准确度。虽然CEEMDAN-Hilbert-CNN提高了故障诊断准确率，但是在CEEMDAN白噪声标准差选取方法尚存在不确定，需要经过无数次实验选取最恰当的白噪声标准差，且未将提及算法复杂度与已存算法进行比较，因此如何自适应选取最适合的白噪声标准差以便更高效更准确的进行诊断任务是值得进一步探讨解决的问题，并考虑把算法复杂度的研究作为下一步研究的问题。