基于波束跳变的地球同步轨道卫星网络管理策略研究

叶 磊

（中国电子科技集团公司第五十四研究所，河北 石家庄 050000）

1 系统模型的构建

1.1 跳波束的时隙模型分析

在处于多波束卫星系统中，波束赋形天线在这个区域内会形成K个点波束，Btot为总带宽，可使用跳波束将系统总带宽以实际作为单位均匀分配给各波束，总长度为W，Ts为最小时隙分布单元，系统能够根据各部分波束业务需求为其分配对应的时隙。通用跳波束允许Nmax个波束在同一时隙内工作。为简化该系统需要均匀进行分簇，第i簇频谱效率为ηi，则分配给该处的容量如下公式所示。

利用跳波束系统实际分配矩阵T能够用于表示波束与时隙之间的关系，在该公式中T（i，j）=1可表示时隙j分配给波束i，而T（i，j）=0则表示时隙j未分配给波束i。

1.2 同频复用距离

在系统中跳波束系数能够分为全频率复用以及部分频率复用，在使用部分频率复用过程中，卫星总带宽能够被分段，每个不簇只有部分带宽处于工作状态，这种方法是以牺牲频谱利用率作为代价，进而能够避免同频率干扰。而在使用全频率复用的基础上，每个簇处于工作状态的用户波束可使用卫星整个可用带频，其能够显著提升频带利用率。因此本研究使用全频率方案。为能够减轻同频因素的干扰，对于较远距离波束可使用空间隔离的方式实现复用，对于较近距离波束可通过时间隔离的方式实现复用，并引入了左、右旋极化，结合国际电信标准要求信噪比与频谱效率曲线为分段函数，表示不同信噪比对应相同频谱效率。

使用相同频率波束处于工作状态时不可避免会出现同频干扰的问题，但有同频干扰的基础上能够确保系统频谱效率保持不变，进而计算同频复用距离是切实可行的。假设功率足够的基可满足业务需求，且各波数分配功率一致。根据文献同频率的干扰增益因子如下公式所示。

在该公式中J1和J3分别能够代表第1节和第3阶第1类贝塞尔函数，信号入射与波束中心指向夹角为R=H为各点波束半径，λ为信号波长，RD为同频复用波束圆心距离，卫星轨道高度为H，上下行链路的SINR，可分别将其表示为SINRup和SINRdown，如下公式所示。

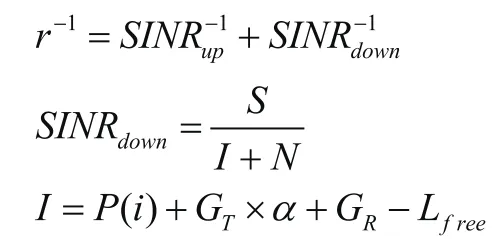
通过对该公式进行计算可获得信噪比，从距离较远波束增加同极化波束，结合国际电信标准中信噪比和频谱效率的关系，可以发现在距离为2R位置时增加同极化同频波束，会减少频谱效率。对于距离较近波束能够通过左、右旋极化的方式能够防止同频干扰，但无法避免由于中心波束位置错开时隙分配的干扰。

2 跳波束时间分片机制

跳波束时间分片以及波束驻留，构建高效时间分配结构，明确具体参数是跳波束系统目前急需解决的问题，结合全局资源实现高效调度的目的，并将提出基于时间分片机制，可通过动目标优化以明确关键参数。

下列参数中跳波束时隙即BHS，是指波束驻留时间，是分配给某一波的最小持续时间。根据容量需求以及qos给各波束对应时间实际个数，跳波束时隙是物理帧时间载体，其通常是以毫秒为单位的。跳波束周期即BHP，是指一次电力分配的跳波束时隙序列需花费的时间，各个波束所处突簇集合是通过动态分组策略来获取，所分配的各跳波束时隙个数以及周期顺序是由波束跳变策略来获得的。时隙切换时间即SS，是指保护时间，从一个波束切换到另一个波束需要耗费的时间延迟，可在一个或多个跳波束之后开展。波束重访时间即RVT，是指各波束将所分配的跳波束时隙资源块彼此之间的间隔时间，由于波束重访的时间通常比较大，会从一定程度上影响用户终端同步，即便在特定跳波束周期中某波束无业务需求，但需要在该周期分配一个跳波束值，并且在该时隙中进行广播、同步等信令。跳序号即HN，是指跳波束实际序号，其也是跳波束时隙数字标识符，通常第一个跳序号为1，在每个波束结束之后可重新初始化为1。当其与波束标识符成对使用情况下，跳序号作为惟一标识符。跳波束时间计划即BHTP，是指资源动态分配时间，分别阐述计划包含各部波束所分配的跳序号以及带宽、载波频率等相关参数。跳波束时间计划需要结合用户的申请业务，感知系统资源等多个因素，是根据网控中心提前生成的，能够发送给地面系统以及卫星系统等。

从跳波束周期以及波束驻留的时间优化来看，在整个波束跳变周期中，系统资源全局调度周期可以用Tw表示，波束驻留时间中资源调度最小单位为Td，波束跳变周期为Tw以及波束驻留时间Td是系统资源高效利用的基础。其中Tw表示能够用于支持波波束数越多，但也会导致时延增加，Td越小表明系统资源的分配灵活性越强，但由于各波输出的时间需同步捕获时间，如果Td越小会导致资源利用率降低。综合分析需要使用多目标优化的方式，以实现对波束跳变周期以及波束驻留时间实现同步优化，在满足系统业务需求前提下，进一步实现全局资源的高效调度。如下公式所示为多目标数学优化模型。

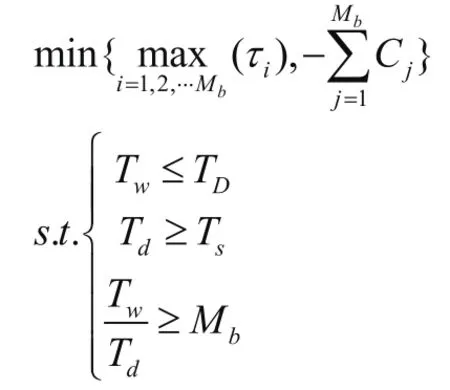
在该目标函数中，第i个波束通信试验间隔可以用τi表示，第j个波束分配系统容量用Cj表示。上述两个目标函数能够分别用于簇内波束最大通信时间间隔以及分配的总吞吐量。在处于约束条件下，簇内波束数目为Mb，系统同步最大保持时间为TD，波束同步捕获时间为Ts，针对多目标优化的问题可采用整数规划、神经网络、最优化设计方法，进而确定复数跳变周期以及波束驻留时间。

3 波束跳变准则

结合业务需求可获得跳波束周期范围内各波束分配的跳波束时隙个数，尤其需要确定簇内部波束跳变条件图案设计，该问题可转换为跳波束周期中各波束的跳波束时隙排序问题。在处于某个跳波束周期范围内，簇内波束可结合是否存在业务传输需求可将其分为非热点和热点区域波束，各个波束跳变策略以及具体流程需要遵循一定准则：

（1）对于热点区域的波束系统其需要结合用户的业务申请，并结合资源分配算法，能够对热点区域的波束分配情况和对应波束间隙完成业务服务。

（2）对于非热点区域的波束则需要考虑波束重访时间影响，主要是由于重返时间较大时会从一定程度上影响用户终端同步，即便处于非热点区域其波束在特定跳波周期范围内无明显的业务需求，这种情况下也应当在周期范围内分配给一个时间波束时隙，且在该时隙中完成广播、同步等相关信令。

（3）对于热点区域的跳波束时隙以及非热点区域的跳波束间隙可实现交替排序，进而能够使终端用户同步最大保持时间与波束重访时间满足下列公式。

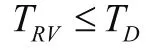
在处于相同信道条件下，如果系统的波束业务需求较小，此时利用N阶差分目标函数能够忽略减少波束，而对于高业务需求波束来说，则能够分配到更多的资源。公平性目标函数能够确保整个系统的公平性，进一步为高业务需求分配相同资源。如果信道条件发生变化，则会结合各波束业务需求，利用公平性目标函数进行公平分配，以确保各波束业务需求能够获得相同满足率。而在信道条件不同时，使用N阶差分函数此时系统信道条件相对较好的波束相比信道较差的波束能够获得更多容量，因此需要结合实际系统参数和容量需求，选择合理的优化原则。

4 结束语

总而言之，在本研究中针对地球同步轨道卫星网络中波束跳变策略进行探究，利用该网络采用跳波束策略进而实现用户控制类信息传输，应用跳波束时能够从一定程度上改变过去信令接入的方式，通过分析跳波束的运行压力以及跳变策略，以实现系统资源的合理调度和高效利用，以期能够提升地球同步轨道卫星网络管理能力以及响应能力。