层次变分高斯混合模型与主多项式分析的故障检测策略

李元，杨东昇，赵丽颖，张成

（1 沈阳化工大学信息工程学院，辽宁沈阳110142； 2 沈阳化工大学理学院，辽宁沈阳110142）

引 言

随着现代工业过程自动化与复杂化的增加，生产过程的故障检测逐渐成为影响工业设备生产效率的重要因素[1-2]。由于工业过程历史数据的可信度日益增强，目前基于数据驱动的故障检测方法得到了广泛关注[3-5]。其中，基于数据驱动的故障检测方法包括主成分分析(principal component analysis,PCA)，核主成分分析(kernel PCA,KPCA)与主多项式分 析(principal polynomial analysis, PPA)等[6-8]。PCA是一种线性假设模型，在线性过程中具有优异的性能，但是当过程变量间存在较强的非线性特征时，其检测性能表现较差[9]。为解决非线性问题，KPCA方法被引入到故障检测领域中，通过核函数映射将数据映射至高维空间，然后在高维空间中使用PCA进行故障检测[10-11]。核函数映射的性质使得KPCA具有较高的计算量与较差的可解释性等缺点[12]。因此，PPA被提出用于非线性故障检测[13-14]。PPA是一种利用回归函数拟合并消除非线性特征的多元分析方法，能够有效克服基于核函数的非线性方法计算量高与解释性差的缺点，近年来得到人们的广泛关注[15-16]。

基于上述分析，PCA、KPCA 与PPA 方法均适用于单模态故障检测，而应用在多模态工业过程中具有较高的误报漏报情况[17-18]。为了解决上述问题，高斯混合模型(Gaussian mixture model,GMM)及其改进的聚类方法被提出[19-20]。GMM假设过程数据由多个局部模型描述，且每个局部模型对应多模态过程中的一个工作模态[21-22]。但是在实际过程中，由于对过程中模态数量的先验知识了解不足，GMM 无法建立合理数量的局部模型。为了解决GMM 局部模型数量求解的问题，有限高斯混合模型(finite Gaussian mixture model, FGMM)与变分贝叶斯高斯混合模型(variational Bayesian Gaussian mixture model, VBGMM)被提出。其中，FGMM 利用最小信息长度准则(minimum message length, MML)选择模型的最优数量[23]。在FGMM 中，首先计算当前模型参数的极大似然估计，再对分布参数重新估计以获得最大的数据似然，最后通过将混合系数设为0 以此消除无效的局部模型[24]。但是，当局部模型描述的数据范围缩减至单个样本时，协方差的奇异导致极大似然估计的迭代求解过程中止，使得模型无法被成功训练。而在VBGMM 中，通过一组概率分布函数描述模型的参数[25-26]。首先，采用一组先验分布描述各模型的参数[27];然后，通过变分推断寻找一组变分概率分布近似观测数据的后验概率[28];最后，通过对联合概率分布期望最大化的迭代过程确定最优的模型参数分布函数[29]。由于VBGMM 是一种对模型参数近似推断其概率分布的模型，因此避免了点估计中奇异矩阵的出现，有效地提高其泛化能力且降低了过拟合发生的可能，故VBGMM 在多模态过程中具有准确的模态识别能力[30]。但是，当VBGMM 的初始模型参数少于实际过程中包含的工作模态数量时，将造成分解的局部模型数据中仍包含多个工作模态，从而影响后续检测模型的性能。

针对工业过程中包含的多模态与非线性特征问题，本文提出一种层次变分高斯混合模型与主多项式分析(fault detection based on hierarchical variational Gaussian mixture model and principal polynomial analysis,HVGMM-PPA)的多模态非线性故障检测方法。首先，通过初始VBGMM 模型将过程数据分解为多个子块；然后，利用具有多个局部模型的VBGMM 将各子块再次分解为附属子块，并将附属子块的信息作为模型参数对VBGMM 进行重构；接下来，将重构的VBGMM 作为初始模型重新分解原始过程数据，重复上述步骤直到每个子块均无法分解时停止；最后，在每个子块内建立局部PPA 模型将各子块数据分解为主多项式空间与残差空间，并分别在其各自的子空间中计算T2和SPE 统计量进行故障检测。通过数值例子与Tennessee Eastman(TE)过程的仿真验证本文方法的有效性。

1 主多项式分析

假设过程数据X ∈ℜd×N含有N 个训练样本，d个变量，且X =[x1,x2,…,xN]。PPA 对数据的第p 步分解如下所示：

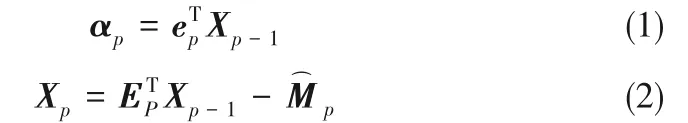
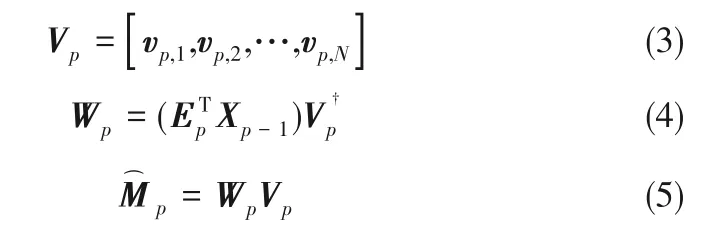
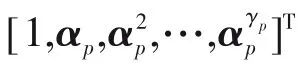
式中，p 的取值为κ～1，当p = κ 时xp= 0(d-ρ)×1。此外，以上统计量的控制限由核密度估计获得[2]。

2 层次变分高斯混合模型与主多项式分析的检测策略

假设观测数据X ={x1,x2,…,xN}包含N 个样本，同时将潜在变量记作Z ={z1,z2,…,zN}，其中zN为1-of-K 的二值向量。在VBGMM 中将观测数据X 与潜在变量Z的联合概率记为：

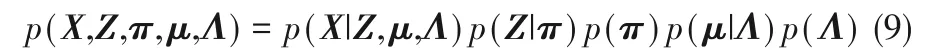
式中，π为混合系数，μ为均值向量，Λ为精度矩阵。p(X|Z,μ,Λ)为给定潜在变量和参数下观测数据X 的高斯分布，p(Z|π)为给定混合系数π 下潜在变量Z 的条件概率，p(π)为混合系数π 上的迪利克雷分布，p(μ|Λ)p(Λ)为高斯-Wishart 先验分布。引入一个变分概率分布q(Z,π,μ,Λ)用于分解潜在变量与模型参数，分解形式如下：

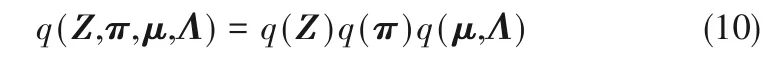
首先，通过变分推断求解变分概率分布q(Z,π,μ,Λ)分别在各参数下的最优更新形式如下：

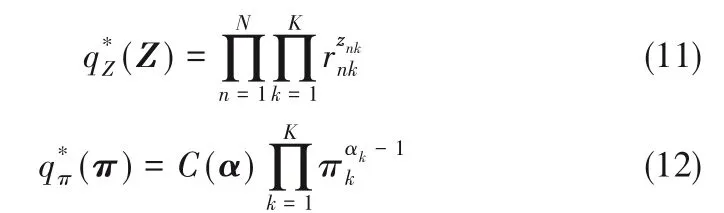
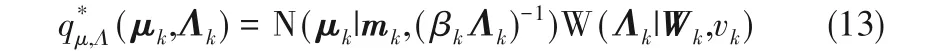
式中,K 为模型假设的高斯分布数量，C(α)为迪利克雷分布归一化系数且α ={α1,α2,…,αk}，πk为第k个组分的权重系数，mk和(βkΛk)-1分别为参数μk的高斯分布的均值与精度，vk为Wishart 分布的自由度，Wk为尺度矩阵。rnk为第n 个样本属于第k 个组分的响应系数，由式(14)解得：

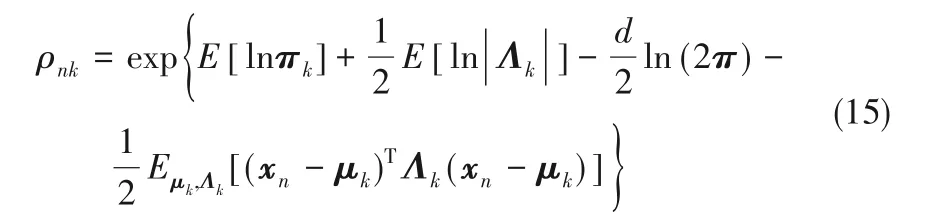
然后，为使得概率分布的更新形式表示简洁，定义观测样本与响应系数相关的统计量，即：

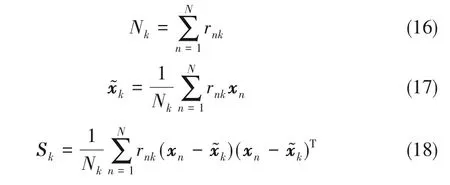
式中,Nk表示第k 组分内关于观测样本的累积响应度，x～k为第k 个组分的均值，Sk为第k 个组分的协方差矩阵。

最后，利用样本与响应系数相关的统计量更新q(π)与q(μ|Λ)q(Λ)的分布参数，更新形式如下：

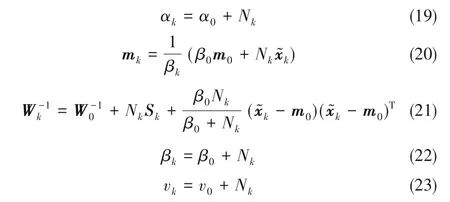
当VBGMM 模型收敛后，对于解释样本无效的组分满足rnk≈0,Nk≈0使得混合系数π的变分布未能与参数的先验分布区分，而有效组分的π 变分布能够偏离参数的先验分布，从而得到混合数据中最优组分数量。

通过上述步骤构建的VBGMM，对过程数据X中的每个样本x 计算所属组分Ck的后验概率，计算方式如下：

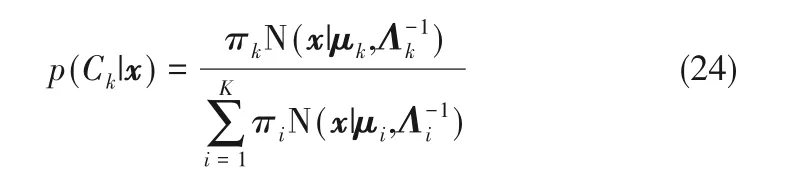
然后将过程数据X按所属的组分划分为多个子块，如式(25)所示：

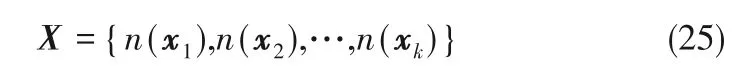
式中,n(xk)表示第k个子块内的样本集合。

下面通过多模态数值例子对VBGMM 进行仿真实验。假设有三个不同模态的数据，其数值例子的生成模型如下[31]：

式中,e1～e3服从均值为0、方差为0.01 的高斯白噪声，通过改变s1和s2来调整系统的操作模态。在 模 态1 中，变 量s1和s2分 别 服 从[20,0.8]、[1,1.3]的高斯分布；在模态2 中，变量s1和s2分别服从[5,0.6]、[20,0.7]的高斯分布；在模态3 中，变量s1和s2分别服从[16,1.5]、[30,2.5]的高斯分布。每个模态各生成400 个样本，累计1200 个样本作为训练数据。

将VBGMM 应用于上述多模态数值例子，由图1(a)可以发现，VBGMM 的初始参数选择不当导致同一子块(如子块A)内包含多个模态的数据，使得模态识别的性能降低而给后续的检测过程带来不利影响。此外，由图1(b)可以看出，VBGMM 分解的子块内存在多个子块(如子块B 与C)同时描述相同模态数据的情况。此时，由于子块B 或C 内不存在多模态特征，所以并未对检测过程产生过多的不利影响。本文为了解决子块内存在多个模态数据的问题，提出一种HVGMM 方法用于确保每个子块数据内仅存在单一模态。

在HVGMM 中，首先使用随机初始化的VBGMM 分析多模过程数据X 并得到各组分的信息。其次将X 分解为多个子块，在各子块数据中再使用VBGMM 分解子块数据为附属子块，并统计各附属子块的均值、精度等信息。然后将上述步骤中附属子块的局部信息作为的模型参数，对VBGMM 进行重构。最后将重构VBGMM 再应用于原始过程数据X，重复上述迭代过程，直到每个子块数据均无法再次分解。上述过程具体流程图如图2 所示。

将HVGMM 应用于上述多模态数值例子，首先使用随机初始化的VBGMM 对过程数据进行分解。若VBGMM 初始分解结果如图1(a)所示，则分别在A与B 子块内再次利用VBGMM 分解。如图3 所示，A子块所包含的数据仍能被分解为两个附属子块，而B 子块仅能分解出单个附属子块且与原始B 子块分布相同。此外，由图3 还可以看出修订后的子块概率边界已经有效地描述了多模态数据的各模态特征。

若VBGMM的初始分解结果如图1(b)所示，此时同一模态数据同时被多个子块描述。但是子块B与C 内的数据经过VBGMM 仅能再次分解出单个附属子块，其分解后的附属子块分布如图4所示。由图5可以看出，重构后的VBGMM 中各个子块数据已有效地去除了多模态特征。

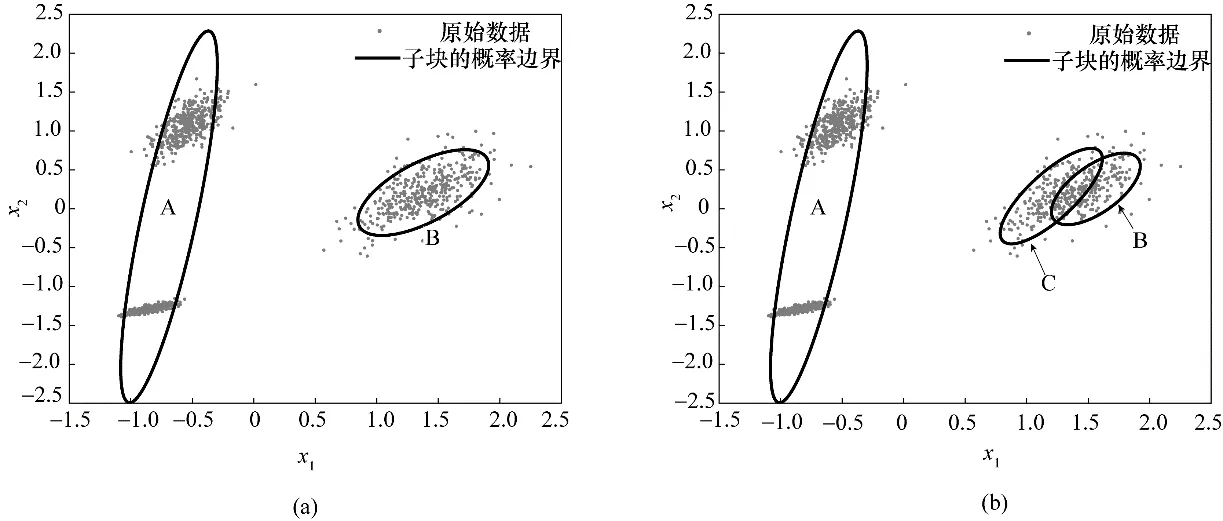
图1 初值选取对VBGMM的影响Fig.1 The initial value selection effect on VBGMM

图2 HVGMM算法流程图Fig.2 The flow diagram of HVGMM

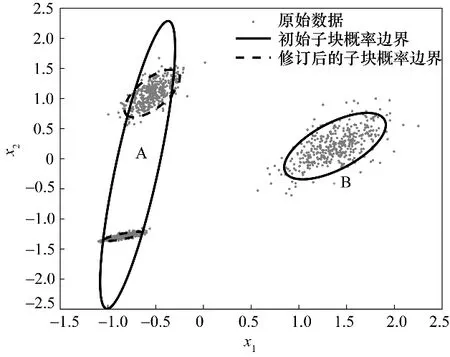
图3 HVGMM分解多模态数据的结果Fig.3 The result of HVGMM decomposition multimode data

通过以上分析，本文提出的HVGMM 能够解决多模态工业过程模态识别困难的问题，降低错误的模态识别给检测过程带来的影响。但是将过程数据分解后变量间仍包含非线性特征，在这种情况下，传统的线性故障检测方法并不适用。而且HVGMM 本质上是一种迭代求解的过程，具有较大的计算量，因此基于核函数的KPCA 方法同样也不适用于后续的故障检测。综上所述，本文将HVGMM-PPA 方法用于故障检测，提高PPA方法在多模态非线性过程中的检测性能。该方法分为离线建模与在线检测两部分，具体步骤如下：

离线建模

(1) 获得正常的多模态过程数据X，并使用zscore方法标准化；

(2) 使用HVGMM 将X 分解为K 个子块数据集n(xk)；

(3)分别在n(xk)子块中构造PPA模型；

(4)在各个子块的主多项式空间和残差空间计算统计量T2和SPE;

(5) 计算出各子块检测模型的控制限CLT2和CLSPE；

在线检测

假设测试样本xnew已经过z-score标准化处理

(1) 计算测试样本xnew属于各个组分的后验概率，并确定其所属子块；

(2)将xnew映射到主多项式空间和残差空间，并计算和SPEnew统计量；

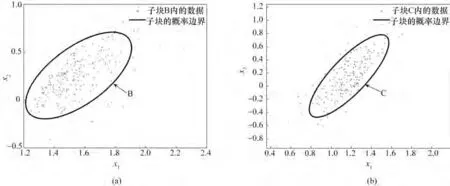
图4 HVGMM分解各子块数据的结果Fig.4 The results of HVGMM decomposition for each sub-block data

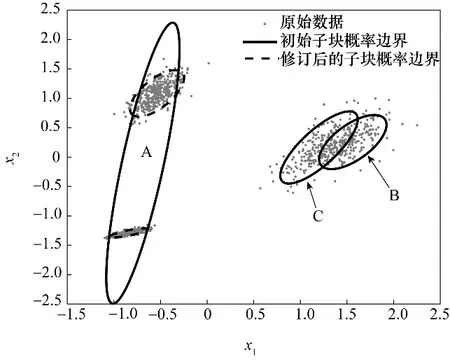
图5 HVGMM的模态识别结果Fig.5 The mode recognition results of HVGMM

HVGMM-PPA的检测流程如图6所示。

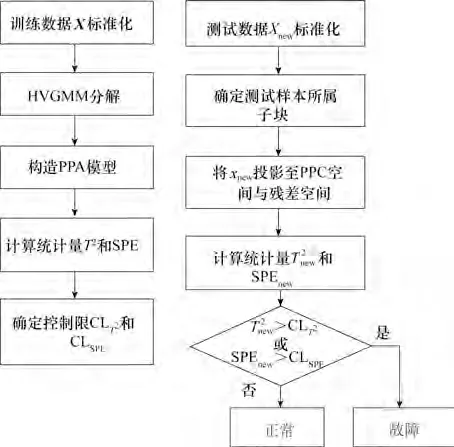
图6 HVGMM-PPA的故障检测流程Fig.6 The fault detection flow chart of HVGMM

3 数值例子

通过在第2节中的多模态数值例子中引入故障样本验证本文所提方法的有效性，其故障生成方式如下：

(1)在模态1的操作条件下，对变量x1从第201～400样本上添加幅值为20%的阶跃故障；

(2)在模态2的操作条件下，对变量x2从第201～400样本上添加0.04(i - 200)的斜坡故障；

(3)在模态3的操作条件下，对变量x3从第201～400样本上添加0.8(i - 200)的斜坡故障。

通过以上步骤在各个模态的操作条件下生成200 个不同类型的故障，将总共1200 个包含各模态故障的样本作为测试数据用于对比实验。

分别利用PCA、PPA 与HVGMM-PPA 对此数值例子进行建模分析。在PCA 中，通过计算方差85%累积贡献率确定主元(principal components, PCs)个数为2。在PPA 与HVGMM-PPA 中根据交叉验证得到PPC 为2，多项式系数为2。三种方法的控制限均设为99%，图7 为VBGMM 对过程数据模态识别的结果。由图7 可知VBGMM 受初值的影响，导致不同模态的样本被分入相同的子块中，使得检测模型对数据分布的假设失效而造成检测模型性能降低。图8 是本文提出的HVGMM 的模态识别效果，由图可知三个模态的过程数据被准确识别。

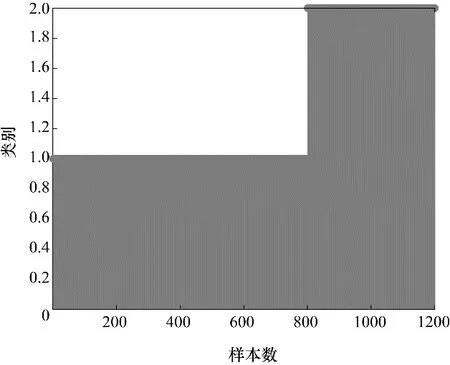
图7 VBGMM的分类图Fig.7 VBGMM classification chart

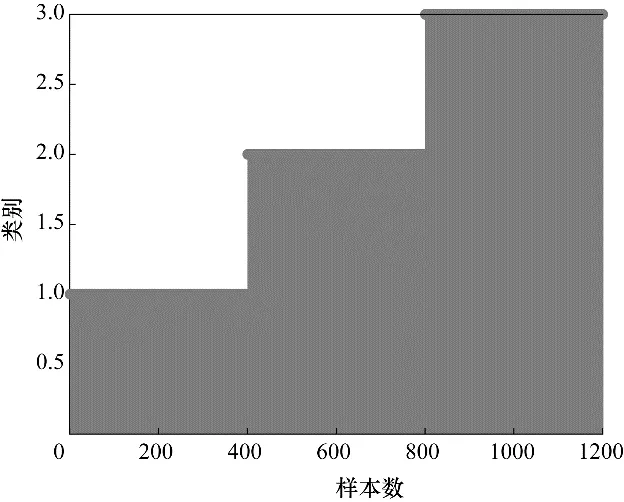
图8 HVGMM的分类图Fig.8 HVGMM classification chart

由图9(a)、(b)可以看出在PCA 与PPA 的故障检测中，由于受到单一模态的分布假设的影响，PCA与PPA 的检测率较低。在HVGMM-PPA 中，通过HVGMM 消除过程数据中的多模态特征，使得每个PPA模型均建立在服从高斯分布的过程数据中。因此HVGMM-PPA 具有较高的检测率，其检测效果如图9(c)所示。以上三种方法对此过程数据的检测率如表1所示。

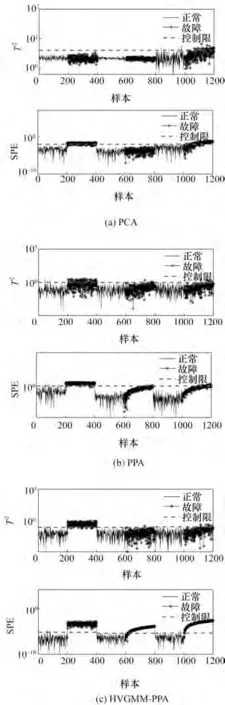
图9 PCA、PPA和HVGMM-PPA检测结果Fig.9 Fault detection results using PCA,PPA,and HVGMM-PPA

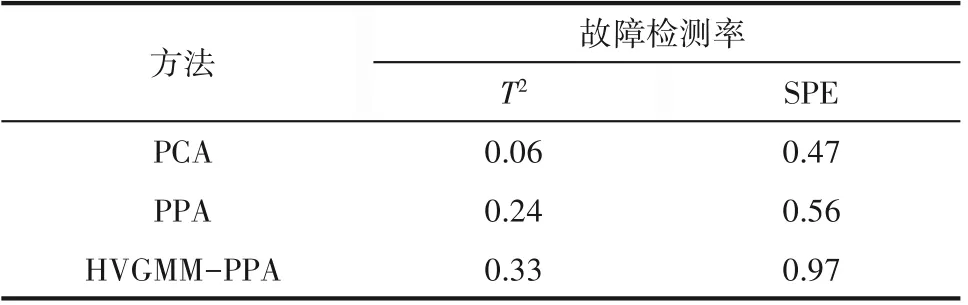
表1 三种方法的检测率Table 1 Fault detection rates of three methods

此外，为了验证同一模态数据被多个子块描述给检测模型带来的影响。过程数据被HVGMMPPA 分解为4个子块且各子块内的类别分布如图10所示。当同一个模态的数据被多个子块所描述时，各子块内的统计信息并未发生显著变化。因此，在这种情况下，由图11可以看出HVGMM-PPA依然能够有效地检测出过程中的故障。

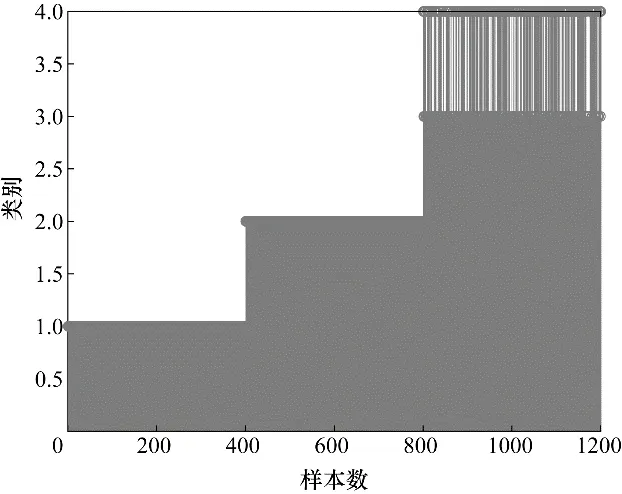
图10 各子块数据的HVGMM的分类图Fig.10 HVGMM classification chart for each sub-block data

图11 HVGMM-PPA的检测结果Fig.11 Fault detection results of HVGMM-PPA

4 TE工业过程

TE 工业过程是由伊斯曼化学品公司创建，是为了评价过程控制和监控方法提供的一个实际工业过程[32]。TE 过程包含12 个操作变量、22 个过程测量变量与19 个组成变量[2,13]。同时，TE 过程包括六种不同的工作模态，具有不同的G/H 质量比，其详细描述见表2[18]。本节使用TE 过程生产模态1和3，并选择11 个操作变量与22 个过程变量作为主要检测变量，其详细信息列于表3。此外，将两个模态共1922 个正常样本用作训练数据，不同操作条件下共1922 个包含故障的样本作为测试数据，其中每个操作条件下的第161～961 个样本为故障。

利用PCA、PPA 与HVGMM-PPA 对TE 进行过程建模分析。在PCA 中，计算方差85%累积贡献率确定的PC 为1。在PPA 与HVGMM-PPA 中，PPC 设为4，多项式系数设为4，其中HVGMM-PPA 建立的局部PPA检测模型数量由HVGMM给出的子块数量确定[13]。三种方法的统计量控制限均设为99%，表4给出PCA、PPA 和HVGMM-PPA 在TE 过程21 种故障中的检测率。由表4 可以看出，HVGMM-PPA 能够检测出TE 过程的大多数故障，为了较好地描述，将表4中最优检测率加粗显示。

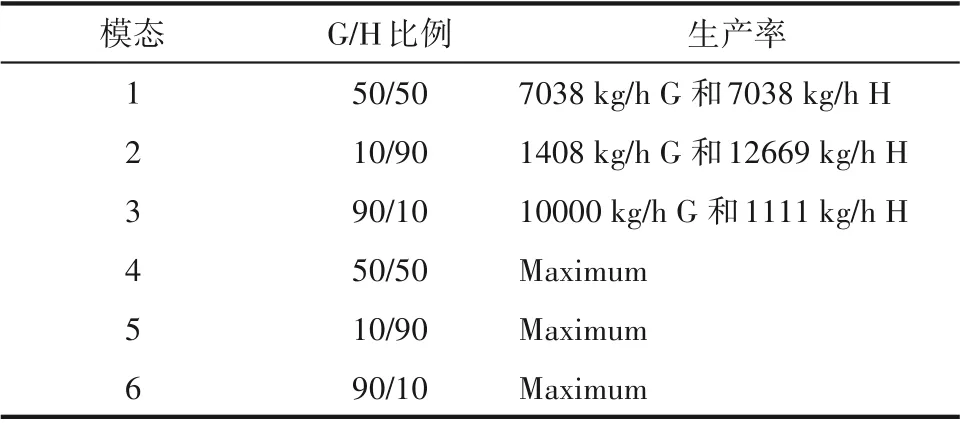
表2 TE过程的工作模态Table 2 Six operation conditions of TE process

表3 用于故障检测的过程变量Table 3 Process variables using in fault detection

由表4 可知，HVGMM-PPA 对TE 过程的21 种故障均具有较高的检测率，同时可以看出PCA 与PPA 在故障1、4、6、8、13、14、17 中仍具有较高的检测率。原因是此类故障中，各个模态数据间的差异并不明显，使得PCA 与PPA 能够识别出过程中的故障。而对于故障2 与故障10 而言，PCA 与PPA 的检测效果较差，因此以下将对故障2 与故障10 进行详细的分析。

故障2是由进料含量的变化使得相关变量偏离正常范围的一种阶跃故障，基于PCA 和PPA 方法均未有效地检测到故障的发生。由图12 可知PCA 的主元子空间中仍存在多模态特征，所以PCA 的检测效果并不理想，其检测结果如图13所示。

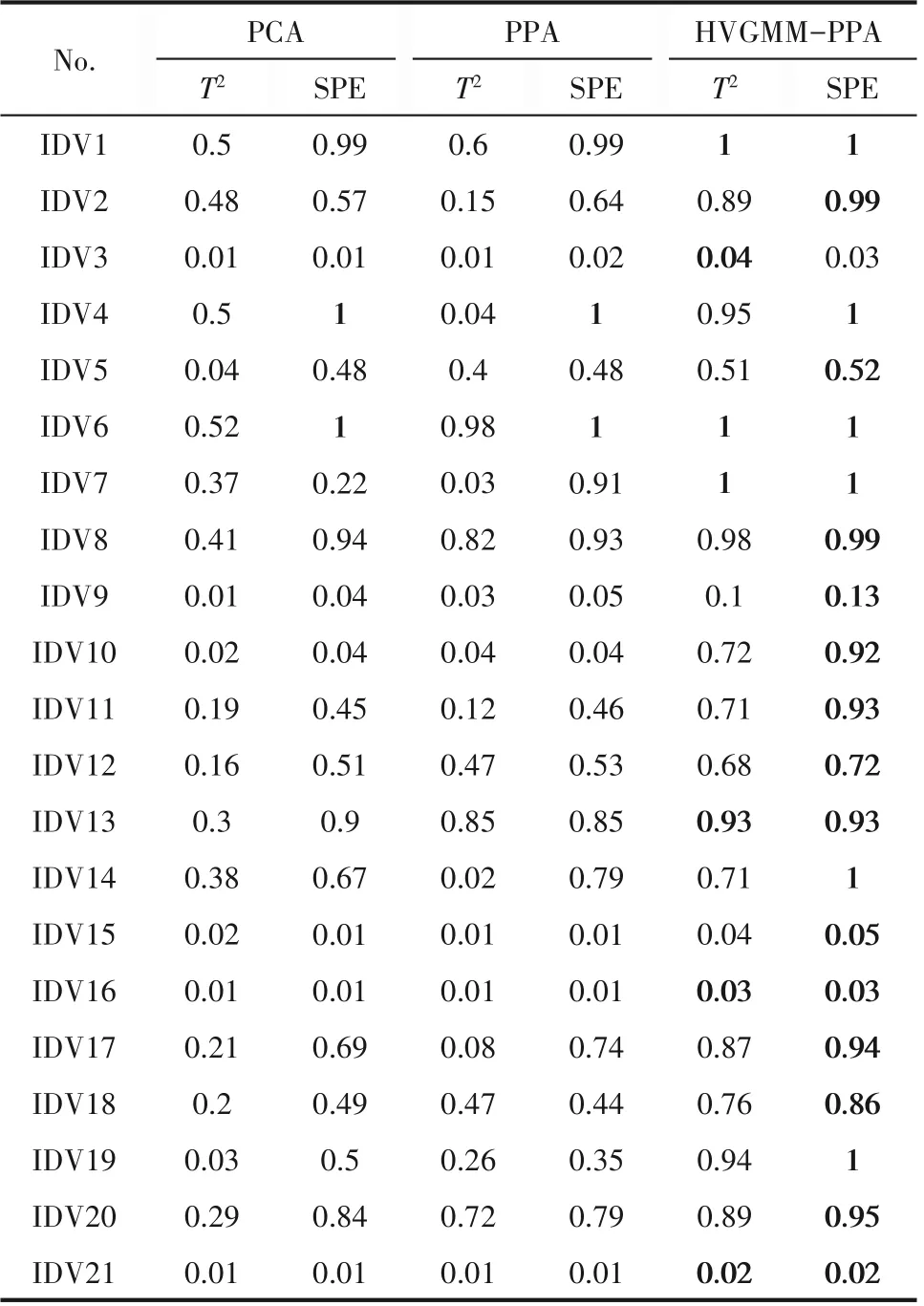
表4 三种方法对TE过程的故障检测率Table 4 Fault detection rates of TE process for three methods

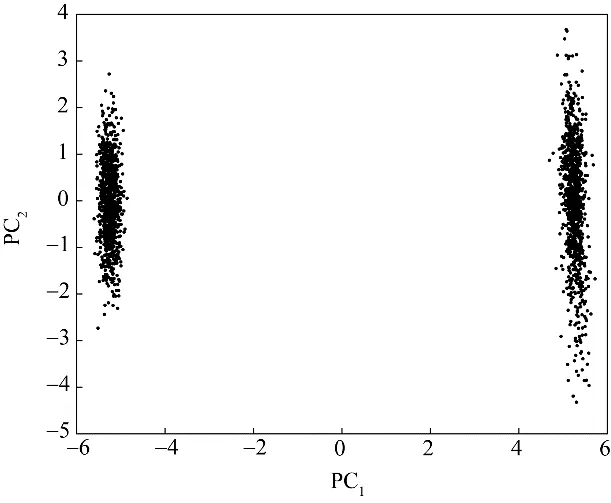
图12 主元空间变量散点分布图Fig.12 The scatter plots of variable in principal component subspace

图13 故障IDV2的PCA检测结果Fig.13 Fault detection results of IDV2 using PCA

同样地，通过图14可以看出PPA 主多项式空间中也包含多模态特征，使得PPA 的检测控制限明显增大。由图15 可以发现，在第1122 个样本之后，故障样本具有偏离正常样本的趋势，但是由于增大的控制限使得模态2 的故障均在控制限之下未被检测。而本文提出的HVGMM-PPA 方法克服了以上缺点，在保证模态识别正确的前提下，构建多个PPA检测模型，避免了多模态特征对检测模型的影响。HVGMM-PPA 的检测效果如图16所示，其结果表现出比对比方法更好的性能。故障10 是一种由C 进料问题随机变化产生的随机故障，PCA、PPA 与HVGMM-PPA 的检测效果如图17 所示。由图17 可以看出，PCA 与PPA 未能检测出各个模态所包含的故障。以上仿真结果均表明，HVGMM-PPA 在多模态工业过程中能够有效地进行故障检测，进一步验证了本文方法的有效性。

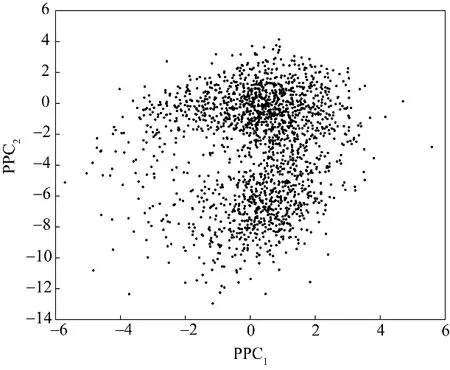
图14 主多项式空间变量散点分布图Fig.14 The scatter plots of variable in principal polynomial subspace

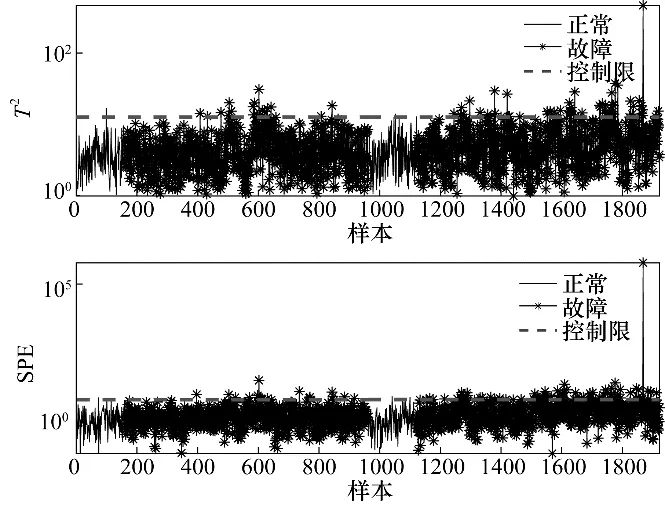
图15 故障IDV2的PPA检测结果Fig.15 Fault detection results of IDV2 using PPA

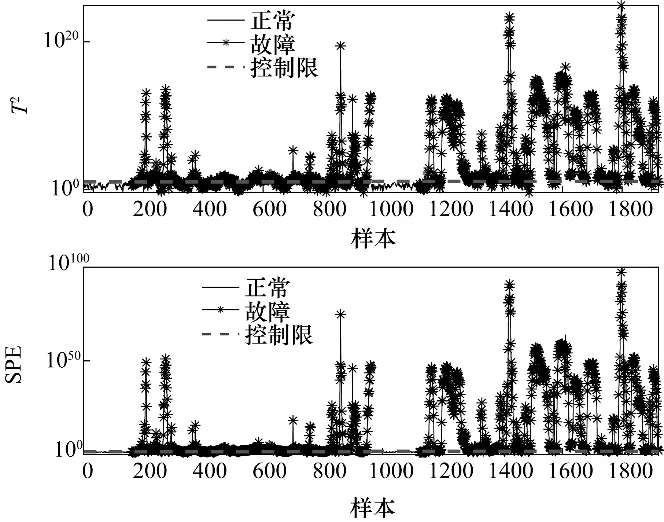
图16 故障IDV2的HVGMM-PPA检测结果Fig.16 Fault detection results of IDV2 using HVGMM-PPA

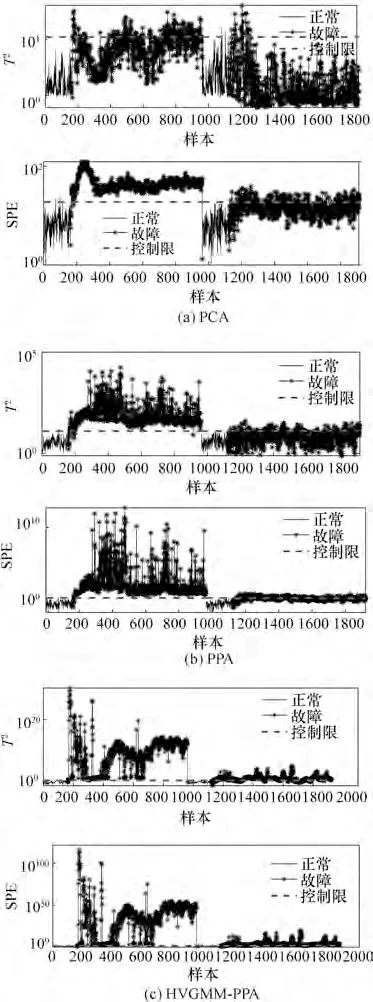
图17 故障IDV10的PCA、PPA和HVGMM-PPA检测结果Fig.17 Fault detection results of IDV10 using PCA,PPA,and HVGMM-PPA

5 结 论

本文提出了一种HVGMM-PPA 的故障检测方法。HVGMM-PPA 不仅可以识别多模态过程的工作模态确定局部检测模型的数量，还可以通过局部检测模型的单变量回归消除过程数据的非线性特征进行有效的多模态非线性过程故障检测。仿真结果表明HVGMM-PPA 模型能够有效避免受到初始模型参数的影响，提高VBGMM-PPA 在多模态非线性过程中工作模态与非线性特征的识别能力。通过数值例子和TE过程的仿真实验，验证了该方法的有效性。