基于特征选择的常减压装置模型及在计划优化中的应用

李勇，钱锋，宋育梅

（1 华东理工大学化工过程先进控制和优化技术教育部重点实验室，上海200237； 2 中国石化上海石油化工股份有限公司，上海200540）

引 言

原油是由多种不同沸点的烃类及其他物质组成的极其复杂的混合物。常减压装置将原油分离成各种中间产品，用于下游装置进一步加工或直接作为最终产品，因此对常减压装置进行建模并将其用于生产计划来提升炼厂的利润效益极为必要[1-2]。常减压工艺流程包括初馏、常压蒸馏和减压蒸馏三部分组成，基本结构如图1所示，初馏塔主要去除原油中的轻质烃类和水，常压蒸馏在常压环境下将大部分原油分解成几种产品，减压蒸馏再利用低压降低馏分闪蒸点将原油的重端分离成几种产品[3-4]。

由于原油通常由大量的化合物组成，其化学成分复杂，故采用原油分析的形式对原油进行定性[5-6]。原油分析通过提高沸点温度，使原油的某些部分蒸发，此温度为实沸点（TBP）。若原油能够实现完全切割，则产品组分的TBP 曲线与原油TBP 曲线重叠[7]，但实际上存在很大差异，如图2 所示。这是由于原油是由多种不同沸点的烃类及其他物质组成的混合物，常减压蒸馏为不完全精馏过程，在原油切割计算时存在误差，导致产品TBP 曲线与原油TBP 曲线有很大差异。在重切割组分中相邻轻组分的浓度较高，导致TBP 曲线与原油TBP 曲线距离较大，由于相邻重组分在轻切割组分中的浓度较低，轻产品的末端与原油TBP 曲线之间的距离较小[8-9]。因此，轻组分的末端和相邻重组分的前端与原油TBP 曲线的距离并不相等，TBP 蒸馏曲线的中点不在原油TBP 蒸馏曲线上[7]。然而，大部分研究均基于两个等距假设：(1)相邻产品的末端与前端点与原油蒸馏曲线等距；(2)产品蒸馏油曲线的中点位于原油蒸馏曲线上。由于实际过程不满足此等距假设，建立不基于此假设条件的产品TBP 预测曲线具有现实意义[10]。

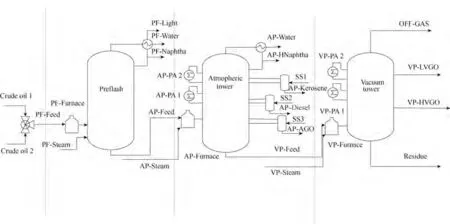
图1 常减压装置Fig.1 Example crude distillation unit

图2 常减压装置原油切割曲线Fig.2 Crude distillation cutting curve for crude distillation unit

常减压装置机理模型能够准确预测常减压装置(CDU)产品收率和性能，Boston 等[11]对精馏塔进行严格的塔板间的模拟，是当今预测宽沸点混合物蒸馏过程的基础，Svrcek 等[12]利用硫含量等特性曲线以及伪组分的混合预测除实沸点曲线外的产品性质。除大规模方程组模型(10000 个方程或更多)来模拟常减压蒸馏过程，也提出了简化常减压装置模型。Brooks 等[13]介绍了固定收率模型，通过预先设定蒸馏物切点，得到固定产量的各蒸馏组分，但是存在切点设置是否最优的问题。根据原油性质、工艺约束和营销策略等条件定义几种操作模式，每一种模式都有一组预定的切点，切点设置来自先前生产设置的经验。Zhang 等[14]介绍了传统的悬摆切模型，并应用在对于相邻切点之间具有相同实沸点组分的摆动上，Li 等[15]针对传统的悬摆切模型存在的问题，改进悬摆切的尺寸以及切割组分的性质，以原油平均累积产量变化为基础，考虑了每种切割产品的重量转移比，来改进悬摆切的尺寸，同时基于原油性质的回归模型来计算常减压蒸馏过程各馏分的辛烷值、API 比重等。Guerra 等[16-17]应用此改进的悬摆切模型改进了具有多个工艺单元和产品混合物的中型整体炼油规划模型。Menezes 等[18]为了提高传统悬摆切模型的精度，把每个悬摆切组分切割成轻组分和重组分来更好的预测蒸馏产品的体积和质量。除上述固定收率模型和悬摆切模型等线性模型外，近几年提出了简单的非线性模型应用于常减压建模的计划优化中，Alattas 等[19]应用非线性规划方法预测单期炼厂运行计划问题，利用分馏指数改进精馏过程的准确性，推导出了一种近似非线性原油蒸馏模型，该模型采用指数逼近的方法，并提出了在不同操作条件下对原油蒸馏指标进行调整的建议。Fu 等[20]利用偏最小二乘（PLS）的方法，搭建了一种应用到计划、调度和实时优化的原油蒸馏单元(预闪蒸、常压和减压塔)的混合模型，从而消除了在决策过程中模型之间的差异，同时该模型不再基于等距假设，改进了之前的模型对产品TBP的预测不够准确的特点。同时Fu等[21]认为不准确的CDU 模型可能导致炼油作业的成本有很大差异。并通过实验验证表明在炼厂的优化模型中使用精确CDU 模型可以获得可观的经济效益，体现了搭建高精度模型的必要性。

本文提出了一种预测常减压装置主要分馏产品实沸点（TBP）曲线的建模方法，针对常减压装置机理模型方程多，非线性程度高、不易收敛等问题，同时考虑到现有的常减压蒸馏过程悬摆切割模型精度不够，且产品实沸点曲线预测不准确，本文在数据建模的基础上提出常减压装置TBP 关系模型，(1)考虑到输出产品TBP不仅与原油的TBP、流量、温度以及塔炉、冷凝器温度等条件相关，同时考虑可以利用输出各百分比TBP 的相关性，通过构建二次项来表征输入输出间的非线性关系，(2)本模型的结构形式通过对非线性方程组求解，得到结构简单且满足精度要求的TBP 预测模型，将该模型成为多输出相互关系模型，并将该模型应用到炼厂计划优化中，并与传统悬摆切割模型对比。

1 基于随机森林的回归模型结构确定方法

1.1 TBP回归模型结构确定

为预测常减压装置各产品TBP 曲线，在建立回归模型中，预测包括初馏塔Light、Naphtha 组分，常压塔HNaphtha、Kerosene、Diesel、AGO 组分，减压塔LVGO、HVGO 组分在内的TBP 曲线，除了与原油TBP、原油混合比、常减压塔的炉温、蒸汽流量等特征相关，产品组分TBP 还与相邻百分比TBP 存在相关性，与传统的回归模型不同的特点在于预测产品某一百分比TBP 时，将产品相邻百分比的TBP 也作为特征，同时加入二次项、交叉项，模型结构如图3所示，模型如式(1)所示：

TBPij是常减压装置i产品j百分比实沸点，其中常减压装置产品i 包括初馏塔Light、Naphtha 组分，常压塔HNaphtha、Kerosene、Diesel、AGO 组分，减压塔LVGO、HVGO 组 分。fij函 数 用TBPa、Tb、Fc和Rmix-ratio各特征表征实沸点TBPij,QAP为常压装置中段回流热负荷。gij函数用TBPPFfeed和TBPie来表征TBPa，TBPPFfeed是原油实沸点曲线，TBPie为常减压装置i产品e百分比实沸点曲线，为TBPij的相邻百分比TBP。hij函数用TPFfurn（初馏塔再沸器温度）、TPFcond（初馏塔冷凝器温度）、TPFfeed（原油进料温度）和TPFstr（初馏塔蒸汽温度）来表征Tb，yij函数用FPFfeed（原油进料流量）、FAPstr（初馏塔蒸汽流量）和Fss1（侧线蒸汽流量）来表征Fc，Rmix-ratio是原油混合比，TBP2a为TBPa二次项，但在构建二次项、交叉项以及特征选择方面具有一定的随机性，并非所有的项均是有效特征，因此需要筛选有效特征，简化模型复杂度。

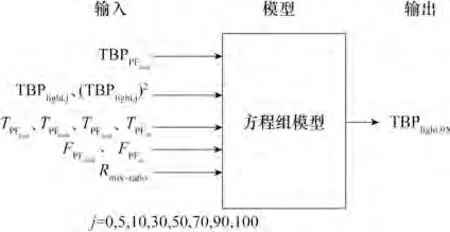
图3 TBP模型结构Fig.3 Model structure of TBP

1.2 基于随机森林的模型结构特征选择

本文利用随机森林[22-23]进行特征选择，特征选择主要通过一系列规则，判断特征重要程度，特征子集相比于原特征集合要小，通过筛选出无关特征减小模型复杂度，提高数据分析效率。随机森林特征选择的主要特点：(1)决策树的生成通过选择部分样本及特征，部分程度避免过拟合情况；(2)决策树的生成随机选择样本和特征，抗噪能力强，性能稳定。

针对上述模型特征结构的筛选步骤如下：

(1)采用Bootstrap抽样从数据集中抽取N个训练集，每个训练集的大小约为原始数据集的2/3，由此训练集建立分类回归树，产生由N 棵决策树组成的随机森林；

(2)从式(1)的TBPPFfeed、TBPlight,j、TPFfurn、TPFcode、TPFfeed、TPFstr、FPFfeed、FPFstr及其二次项交叉项等M 个特征中随机选择m 个特征，以内部节点Gini 系数最小原则来进行每棵树的训练；

(3)对N 棵决策树组成的随机森林对数据集中未参与训练的数据回归，针对变量重要性的评估问题，采用袋外数据误差计算式(1)中M 个特征的重要性，根据袋外数据误差计算随机森林中每个决策树的袋外误差，然后随机改变袋外数据式(1)中M 个特征中的某一特征，并计算新的袋外误差，最后特征的重要性由式（2）表示：

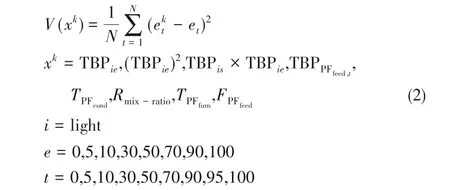
特征的变化引起的袋外误差增加越大，精度减少得越多，说明该变量越重要。因此本文根据随机森林算法的特点，对式(1)的所有特征排序，可得到各个特征对结果预测的贡献，删除掉得分较小的特征，以此来简化模型。

2 基于鲸鱼优化算法的多输出相互关系模型参数优化

2.1 TBP预测回归模型

通过特征选择，得到简化回归模型，以light 组分TBP95为例，见式(3)：

式中，aij、bij、cij和dij为公式参数，在实际建模过程中，当预测TBPlight,95时，式(3)回归模型中的特征TBPlight,s、TBPlight,e均未知，因此，在预测TBPlight,95时，将特征TBPlight,s、TBPlight,e作为未知变量，将TBPa、Tb和Fc公式代入TBPij公式中，将未知变量的参数设为bij，特征变量参数设为aij，以示区分，得到式(4)：

依据上述TBPlight,95推导过程，同理可完成TBPlight,j,j = 0,5,10,30,50,70,90,100 的 推 导 ，将[TBPlight,0,TBPlight,5,…,TBPlight,100]构建方程组，等式左边为包含未知变量的公式，右边为包含TPFfurn（炉温）、TBPPFfeed（原油TBP）、TPFcode（冷凝器温度）等已知变量的公式，把所有的模型联立起来，得到如下的方程组：

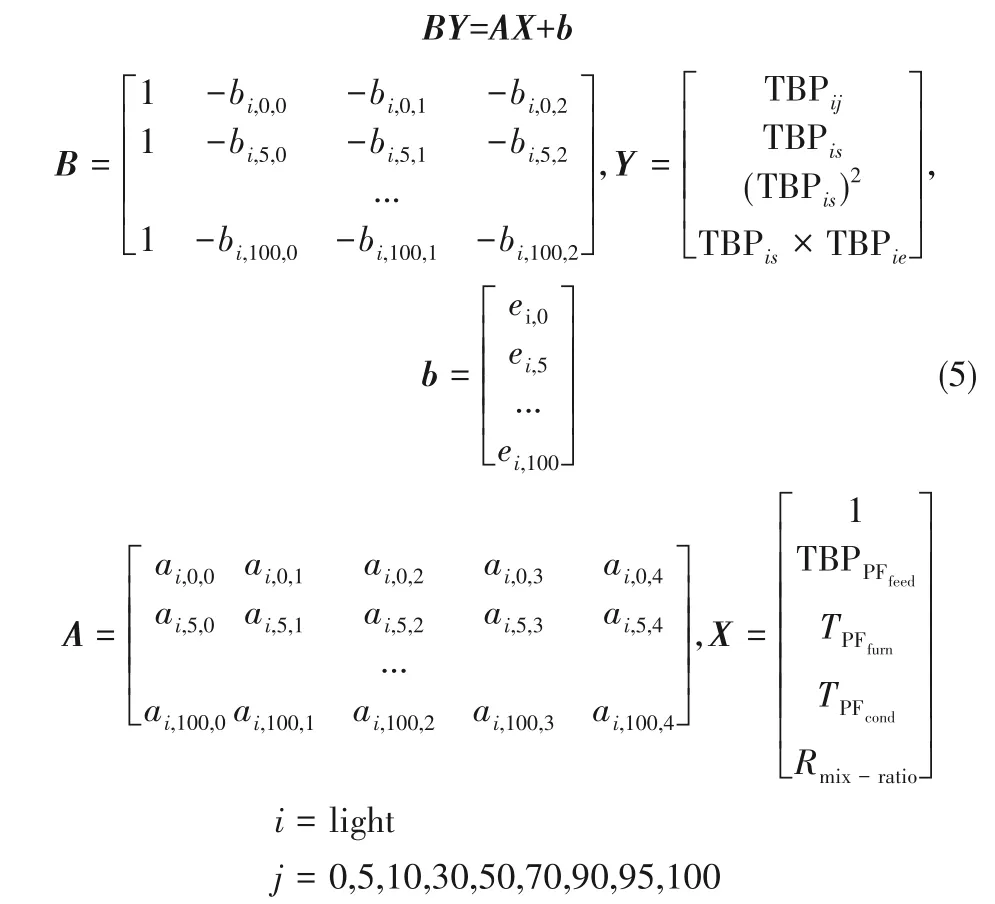
式 (5) 为 关 于 TBPlight,j、TBPlight,i、(TBPlight,i)2、TBPlight,s× TBPlight,e等一次项和二次项的非线性方程组，通过方程组求解器求解得到向量的值。与混合模型[7]的模型结构对比，如式(6)所示，该模型结构通过产品TBP 间的相互关系构建方程组模型，求解联立的方程组可得到预测组分所有TBP 的值，混合模型则是通过分析各百分比TBP 的不同非线性程度分别搭建模型，对TBP 曲线中段搭建线性模型TBPij，前段和后段添加非线性项TBPdij。从表达形式上，本方法综合考虑切割产品的实沸点（TBP）与原油TBP、流量、温度等变量影响，构建非线性方程组模型来表征输入输出间的关系,并利用特征选择方法遴选相关变量（包括进料性质、相邻TBP 及其二次项等），表达形式更加简洁。

2.2 模型参数优化

利用式(5)所示构建方程组的形式描述输入输出间的关系，用机理模型数据对模型进行训练，得到方程组模型存在偏差，若直接对方程组求解，由于等式两端存在偏差且需把部分变量当作未知变量，导致求解结果不够精确，因此利用鲸鱼优化算法对式(5)的矩阵B与常数项b进行参数优化。

2.2.1 鲸鱼优化算法 鲸鱼优化算法(whale optimization algorithm, WOA)是Mirjdlili 等[24]提 出 的一种新的群体智能优化算法，其优点在于操作简单，调整的参数少以及跳出局部最优的能力强[25]。主要步骤如下：

(1)包围猎物 座头鲸在狩猎时要包围猎物，个体与猎物间距离的数学模型如下：

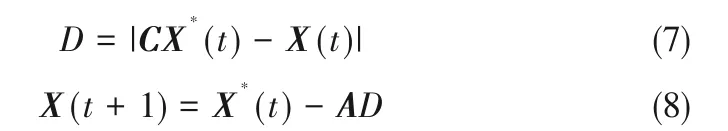
式中，D 为当前个体与猎物间距离，X*(t)表示当前最优的鲸鱼位置向量，X(t)表示当前鲸鱼的位置向量，A和C为向量系数，由式(9)、式(10)得出

式中，a 在[0,2]范围内迭代线性下降，r为[0,1]随机变量。

(2)狩猎行为 根据鲸鱼和猎物的位置建立螺旋运动方程，将狩猎行为的描述成如下数学模型:

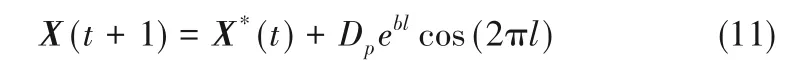
式中，Dp= |X*(t) - X(t)|表示最优的鲸鱼位置和猎物(当前最优解)距离，X*(t)表示当前最优的鲸鱼位置向量。

鲸鱼以螺旋形状游向猎物的同时还要收缩包围圈，根据此两种行为，其数学模型如下

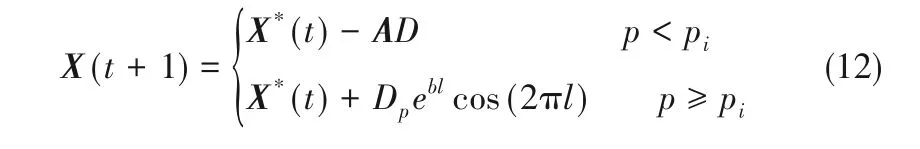
式中，pi是(0,1)中的任意值，取0.5。除此以外，鲸鱼还会随机搜索猎物。

(3) 搜索猎物 在搜索猎物时，其数学模型如下：

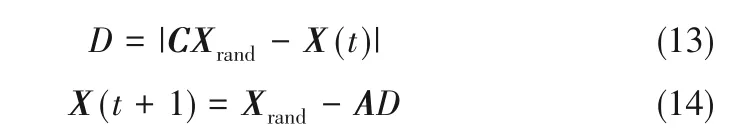
式中，Xrand是随机位置向量，算法设定当|A|≥1时，使WOA算法能够进行全局随机搜索。

2.2.2 目标函数 本优化算法以目标函数适应度值最小为原则，目标函数为该产品TBP 的预测值与真实值的均方根误差，通过判断是否达到最大循环迭代次数为循环终止条件，在模型矩阵参数优化中，目标函数定义为：

3 常减压装置模型仿真分析

为了对初馏塔、常压塔和减压塔的产品组分TBP进行预测，由于工业现场采集数据较困难，存在测量不准，物料不平衡，有大量异常值缺失值的问题，本文利用Aspen plus[26]来采集样本数据，流程图如图4所示。样本采集采用拉丁超立方抽样的方法选取样本点，得到1200组数据，建模过程用其中900组数据作为训练样本，300组作为测试样本。

以TBPlight,95(light 组分TBP95)组分为例，通过随机森林的式(2)得到各个特征权重如表1所示，从表1中可以看出，对light 组分变量TBPlight,95影响权重最大的为该组分相邻百分比TBPlight,s, s = 70,90,TBPlight,e, e = 100及其二次项和交叉项，TBPPFfeed,s对产品性质影响次之，同时TPFcond、TPFfurn等装置的操作变量、FPFfeed和Rmix-ratio对产品预测也有较大影响，并根据此来预测筛选掉(TBPlight,e)2, e = 0,5,10,30,50 等不相邻组分的二次项，等原油重端实沸点，TPFfeed、TPFstr等进料温度影响不大的特征。

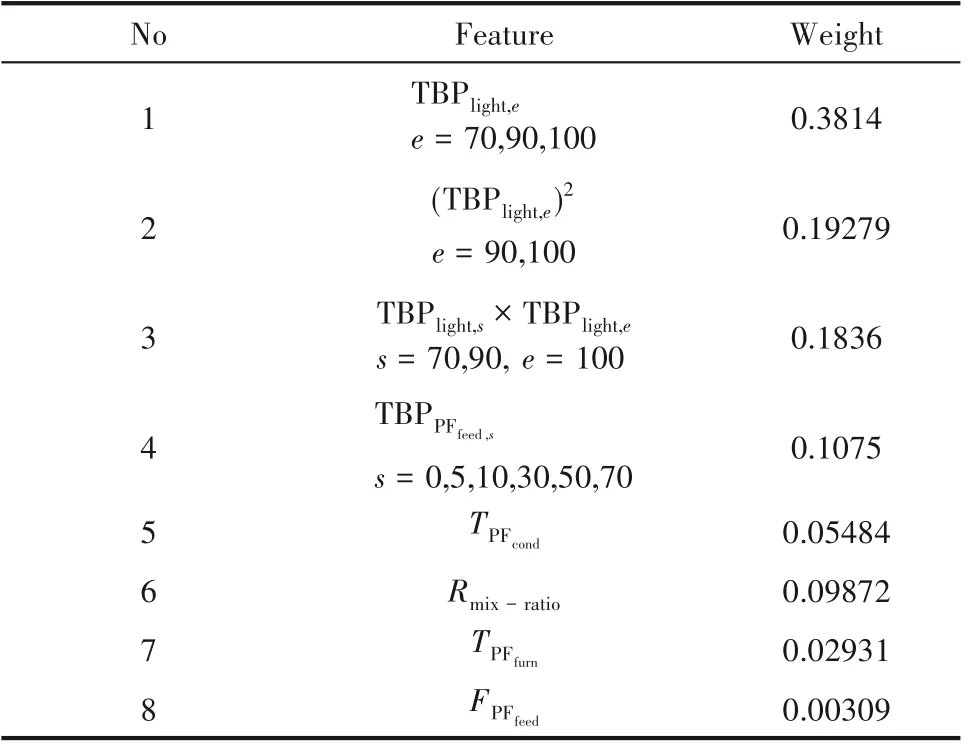
表1 随机森林算法选出的权重排序特征变量Table 1 Weights sort features by Randomforest

图4 常减压装置流程图Fig.4 Crude distillation cutting curve flowsheet

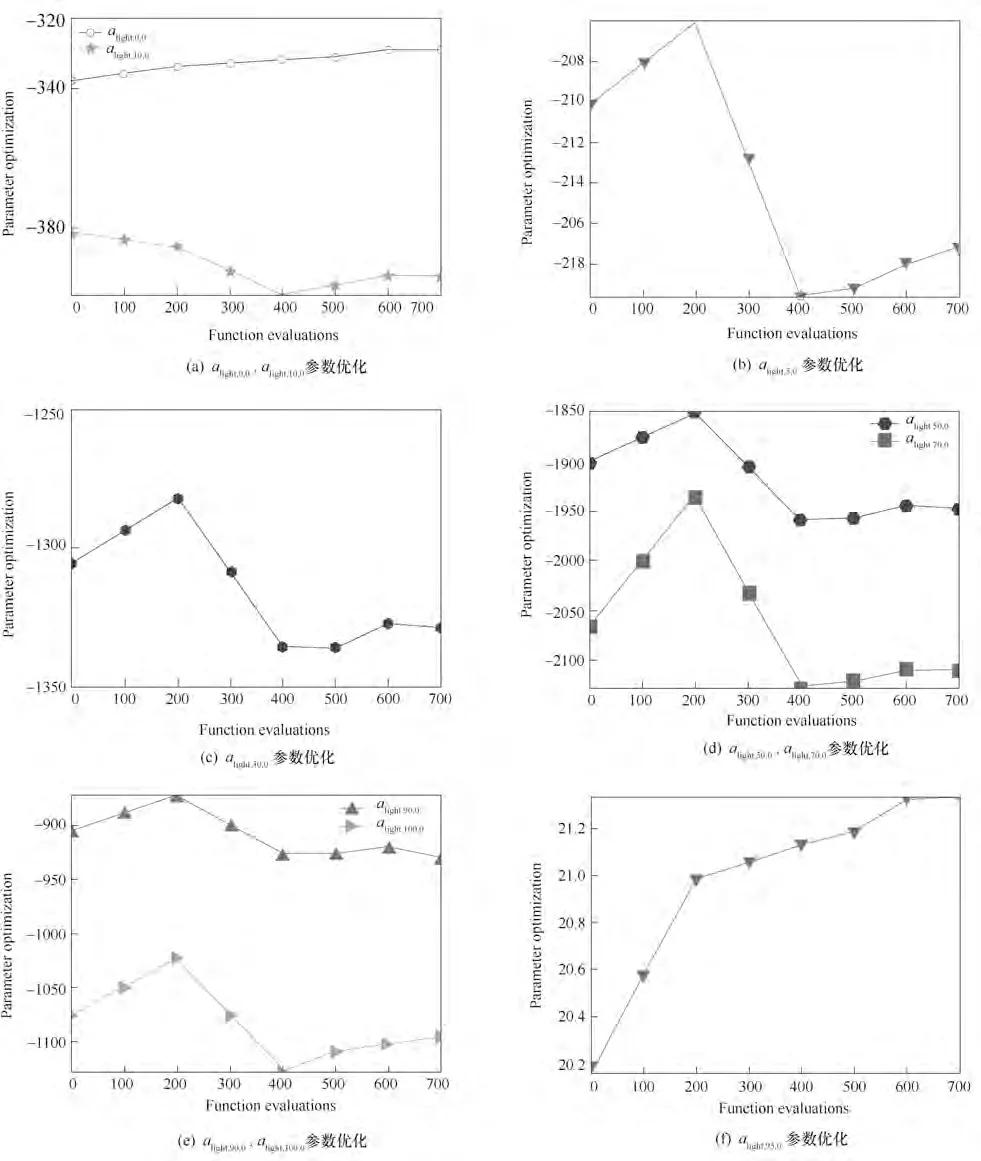
图5 PF-Light组分参数优化Fig.5 The parameter optimization of PF-Light

经过特征选择筛选输入输出变量及其二次项和交叉项，然后将模型构建成方程组模型的形式并利用优化算法对模型参数进行优化，以PF-Light(初馏塔轻组分)TBP 模型为例，式(5)中A 矩阵的常数项参数变化曲线如图5 所示，参数的变化趋势大体一致，在200次迭代以后参数的变化趋势与之前相反，可见优化算法跳出局部最优，寻找到更优的参数。将优化过的参数应用到方程组模型公式(5)中，以此得到预测产品PF-Light(初馏塔轻组分)TBP 曲线的最终的模型。

常减压装置的建模过程包括以机理模型的采样产生数据集，利用采样数据集构建回归模型，针对模型中的一次、二次项特征进行特征选择，简化后的模型构建方程组，并通过鲸鱼优化算法优化参数。接下来，将以机理模型的采样产生的数据作为标准，由于目前常减压装置的模型大部分为线性模型，同时式(6)的混合模型[7]为目前常减压装置兼顾计算效率与预测精度的最优模型，将该模型的精度与线性模型、混合模型结果对比，以平均绝对百分比误差(mean absolute percentage error,MAPE)作为评价指标，其中MAPE表示为式(16):

从图6 可以看出，多输出相互关系模型预测结果在TBP 曲线中段更接近机理模型的TBP 曲线，在前段和末端与混合模型差距较小，经分析，本模型采用方程组的形式，统一对所有预测变量求解，并通过相邻TBP 间相互表征，使得预测精度更高。而混合模型对TBP 曲线中段采用线性模型，对前段和末端添加非线性项，模型预测精度不够。从表2 的平均绝对百分比误差此衡量指标明显发现，本模型误差要明显小于线性模型和混合模型，以PFNaphtha各百分比TBP对比为例，本模型建模结果的平均绝对百分比误差比混合模型平均绝对百分比误差降低了3.4 个百分点，比线性模型降低了4.8 个百分点，可见，该模型在预测产品TBP 曲线时更加精确。

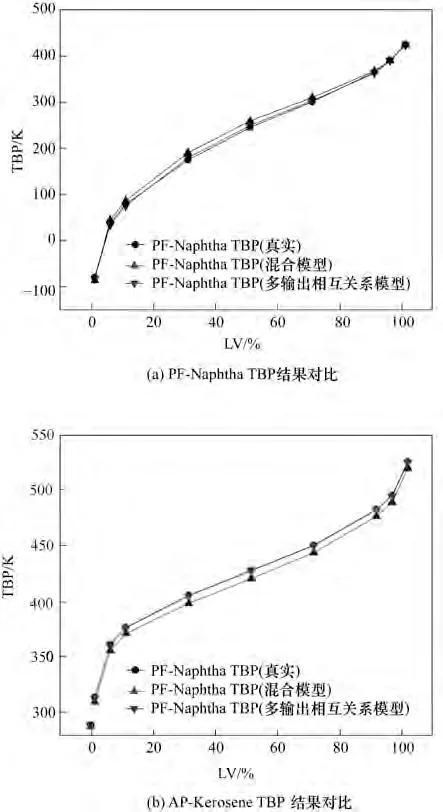
图6 组分TBP预测对比Fig.6 Compared with hybrid model result and true result

经分析，在建模特征选择上，混合模型[7]在建模过程中加入切点温度、每种组分的累计切割宽度，进料密度、汽化热，组分比热容等特征来进行建模，本文所述方法则在预测产品的某一TBP 曲线时，不仅关联原油的TBP、流量、温度以及塔炉、冷凝器温度等条件，同时考虑利用输出各百分比TBP 的相关性，通过构建二次项来表征输入输出间的非线性关系，提高模型精度。此外，混合模型需要先对产品的TBP 进行线性预测，再对前后端的非线性部分进行补全，不能有效保证模型精度；多输出相互关系模型的结构形式通过对联立方程组求解，可同时得到方程组内所有未知变量值，并利用鲸鱼优化算法进一步优化参数，求解方便，收敛性好且精度更高。

4 常减压模型在炼厂计划优化中的应用

炼厂生产计划的目标为生产利润最大化，传统的炼厂生产计划为线性模型，存在无法修正反馈炼厂生产过程，预测精度不够等问题[27-28]，故本文将搭建的非线性常减压模型应用到炼厂计划优化中，并与传统悬摆切割模型对比，在保证模型收敛性和求解效率的基础上，提升计划优化的准确度,同时提高系统对扰动的快速估计,以及对目标的无差别调节[29-30]。

本计划优化模型涉及装置为常减压装置和催化重整装置，常减压装置生产得到的石脑油，作为催化重整装置二次加工原料，经催化重整加工得到高辛烷值汽油和芳烃。本计划优化模型的目标函数为

本目标函数为验证多输出相互关系模型在计划优化中的应用，故简化计划优化过程的复杂度，约束混合原油在进入常压装置的流量以及常压装置用于侧线产品的比例是固定的，此约束可使得混合原油进料量和TBP 与侧线产品直接相关，α 为固定比例，取值0.8。FRG为普通汽油产品流量，FPG为优质汽油产品流量，此两类产品由催化重整装置生产。FKer、FDie分别为煤油和柴油常压装置侧线产品流量。CRG、CPG、CKer、CDie为各侧线产品价格,Coil1、Coil2为两种原油价格，原油和产品价格见表3，FPFfeed为混合原油进料量，Rmix-ratio为两原油混合比例。QAPfur为常压装置中段回流热负荷，MMBtu·h-1(百万英热每小时)；单位功耗费用为5.395× 103USD，CCR为催化重整过程的操作费用，为2.6 USD·bbl-1[1 bbl 代表1桶，1 bbl=137 kg（全球平均）]，与FHnaphtha（石脑油组分流量）相关。

表3 产品和原油定价［15］Table 3 Product and crude oil price

表4 决策变量约束Table 4 Decision variables constraints

针对式（17）目标函数的计划优化问题，采用IPOPT 求解器求解，将求解得到的计划排产结果中各产品收率和石脑油的实沸点曲线与悬摆切割模型寻优结果对比，产品产率和产品TBP 曲线对比分别如表5 和表6 所示。本文将同操作条件下的Aspen 模拟结果看作为实际值，用来验证基于本文常减压模型的计划模型的准确性。

从表5 产品产率和表6 的实沸点曲线对比看出，针对多种侧线组分，本文计划模型一方面可以平衡各产品产率，生产出价格更高的产品普通汽油（RG）和优质汽油（PG），证明了非线性模型的优势。另一方面，与Aspen模型结果对比，本文计划模型获得的产品收率和实沸点曲线更接近相同操作条件下的实际结果。因此，当其作为二次原料进入催化重整装置时，对优质汽油和普通汽油的产量预测更准确。由表4 的决策变量约束以及表7 决策变量前后变化的结果看出，原油1 定价更低，在混合比0.2∶0.8 情况下，可生产更多普通汽油，故原油配比优化为0.2∶0.8，同时常压装置中段回流热负荷能优化到最低。基于上述原因，本模型与传统悬摆切割模型在计划优化中的对比，利润平均提高5×104USD。

表5 产品产率对比Table 5 Product yield comparison

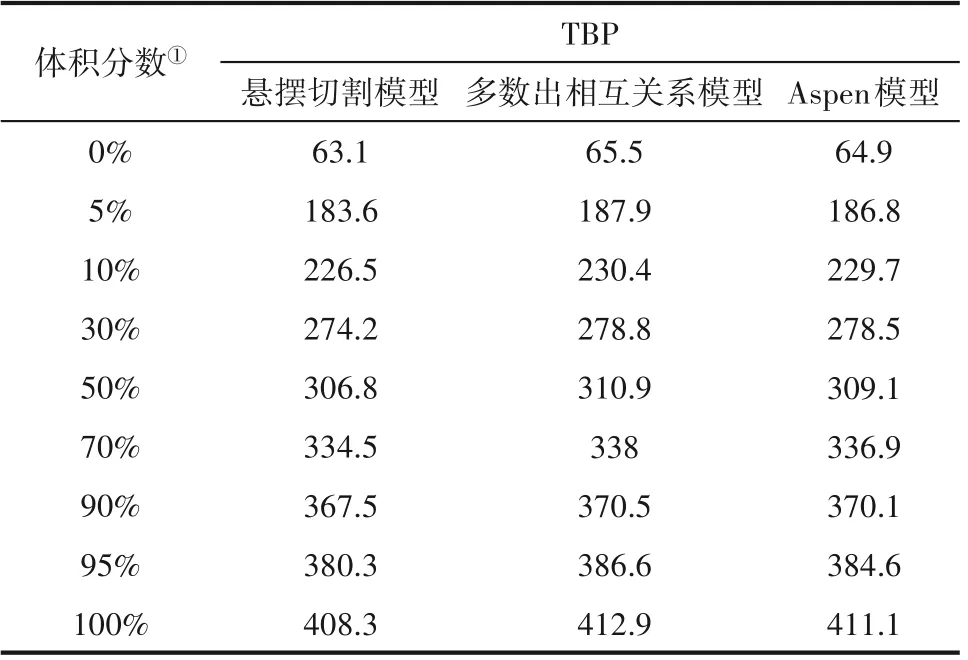
表6 AP-HNaphtha实沸点对比Table 6 AP-HNaphtha TBP comparison

表7 决策变量前后变化Table 7 Before and after changes in decision variables

5 结 论

本文提出了一种考虑相邻TBP 性质的常减压模型，利用输出变量相邻百分比TBP 的相关性，通过构建二次项来表征输入输出间的非线性关系，以此搭建常减压模型，通过随机森林算法进行特征选择，筛选相关性高的特征，利用鲸鱼优化算法优化模型参数，提高模型精度。此常减压模型不仅表示相邻TBP 的相互关系，而且利用相邻TBP 来相互表征，可降低模型复杂性，在后期通过求解方程组即可求得其值。

多输出相互关系模型一方面可解决常减压装置机理模型方程多，非线性程度高，不易收敛等问题，另一方面解决现有的常减压蒸馏过程的建模过程中悬摆切割模型精度不够、产品实沸点曲线预测不准确的问题，并将炼厂生产计划中的多输出相互关系模型与传统的悬摆切割模型对比，得到模型生产利润结果。